基于ANSYS的GK320型密炼机转子的热装配模拟研究

汪传生，张守锋，王孔烁，王志飞，边慧光*

（1.青岛科技大学 机电工程学院，山东 青岛 266061；2.山东省高分子材料先进制造技术重点实验室，山东 青岛 266061；3.益阳橡胶塑料机械集团有限公司，湖南 益阳 413000）

密炼机是一种在可调温度和压力的密闭状态下间歇性地对聚合物材料进行塑炼和混炼的机械，其核心部件是一对特定形状并相对回转的转子[1-3]。转子由转子体和转子芯轴组成，转子体与转子芯轴采用热装配方法实现过盈配合。过盈配合系统具有结构简单、定中心精度和承载能力高、承受交变和冲击载荷性能好等优点[4]。但同时过盈配合系统也会产生一系列的问题，例如在装配或使用过程中可能出现配合面间有过大塑性变形的问题，强化应力集中，损伤零件表面，削弱配合零件的连接强度，进而造成零件松动、振动、磨损和断裂等问题[5]。密炼机在混炼过程中，需要有温控系统来调节胶料温度，在转子内部存在冷却水道，如果转子的热装配出现问题，会出现漏水现象，这在工厂中比较常见。

本研究针对GK320型密炼机转子热装配过程建立转子模型，采用ANSYS有限元软件对不同过盈量下的转子进行温度场分析，并将温度场作为条件进行转子体热变形和热应力分析，以期为转子的设计、加工转子体和装配提供参考。

1 模型建立

1.1 物理模型

ANSYS和CAD软件能较好地建立无缝连接，通过SolidWorks可绘出转子结构体。转子结构模型如图1所示，其中黄色部分为转子体，中间圆柱为转子芯轴。转子体长度 1 012 mm，内孔直径345 mm，最大圆直径 716 mm，转子芯轴长度1 412 mm。

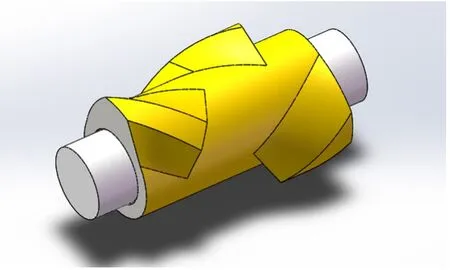
图1 转子结构模型Fig.1 Model structure of rotor

在采用有限元软件进行计算之前，需要对模型进行网格划分，这是有限元数值模拟分析的重要一步，网格划分质量会影响数值计算的精度[6]。本模型根据实际位置进行网格划分，重点细化了转子体与转子芯轴接触面上的网格。转子网格划分模型如图2所示，生成的节点数为672 393，单元数为386 509。

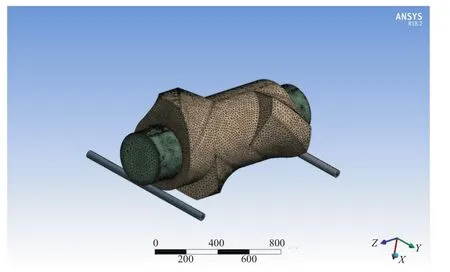
图2 转子网格划分模型Fig.2 Meshing model of rotor

1.2 数学模型

像转子体这种轮廓复杂部件预热后发生的变形是不规则的，主要是因为转子体各部位受热后的变形不尽相同。对于这类形状复杂的机械体的热变形，传统热变形理论对其计算结果存在不精确性，目前较为有效的方法是基于有限元法的热变形计算[7]。

目前，在生产加工中普遍采用函数公式来计算过盈配合系统所需过盈量和装配间隙下的热装配接触压力、导轮与内圈之间的摩擦力、轴向间隙等[5]。

转子体在进行热装配前需要在预热箱内进行预热，使其内孔直径D增大。

式中 ΔD—— 预热后转子体内孔直径增大量，mm；

δ——过盈量，mm；

e——装配间隙，mm。

预热过程中转子体长度L增大ΔL，则

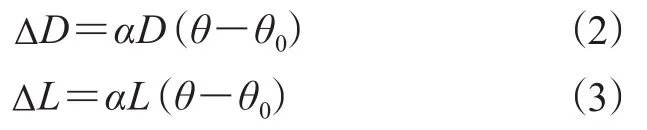
式中 α—— 材料热膨胀系数，℃-1，在此处取1×106℃-1；

θ——预热温度，℃；

θ0——装配环境温度，℃。

将式（2）代入式（1）得

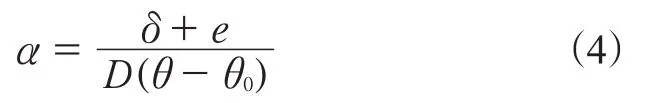
将式（4）代入式（3）得

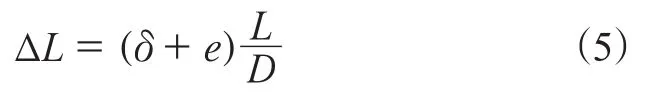
将转子体从预热箱取出安放于预定安装基准后，其温度从预热温度θ开始逐渐下降，进入冷却收缩阶段。由于此时的收缩量小于装配间隙e，收缩不受其他尺寸的约束，称为自由收缩阶段；转子体内孔直径收缩量达到装配间隙e时，转子体与转子芯轴发生接触，此时收缩受到尺寸约束的影响，称为约束收缩阶段。从自由收缩阶段到约束收缩阶段的转子体温度θc为

式中，d为转子芯轴外直径，mm。

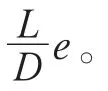
理论分析中假设转子体长度收缩是相对于轴心线对称分布的，则自由收缩阶段转子体长度收缩量ε1为

在约束收缩阶段中，转子体与转子芯轴发生接触后继续收缩而使转子芯轴受压，反作用力作用在转子体内孔表面，转子体内孔表面压力P为

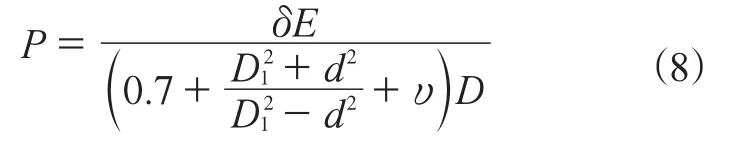
式中 E——弹性模量，Pa；

D1——转子体外直径，mm；

υ——泊松比。

由于转子体轴向收缩，转子体与转子芯轴产生的摩擦力τ为

式中，f为摩擦因数。

由于摩擦阻力的影响，转子体轴向收缩量减小，摩擦力使转子体轴向收缩的减小量λ为

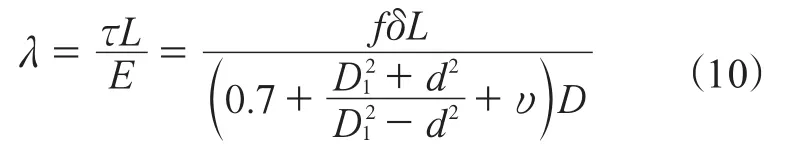
约束收缩阶段转子体长度收缩量ε2为

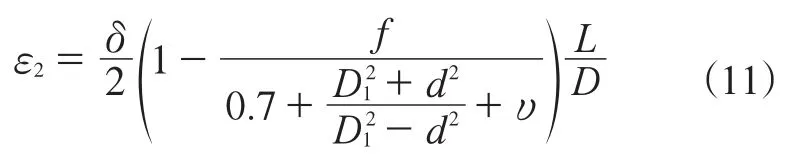
当不计重力作用时，转子体长度总收缩量ε为自由收缩阶段和约束收缩阶段收缩量之和，即

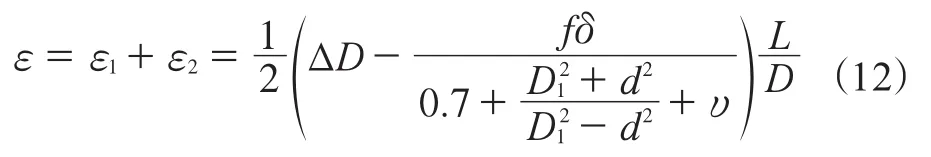
不计重力作用时，转子体长度总收缩量ε仅计算约束收缩阶段转子体长度收缩量，即

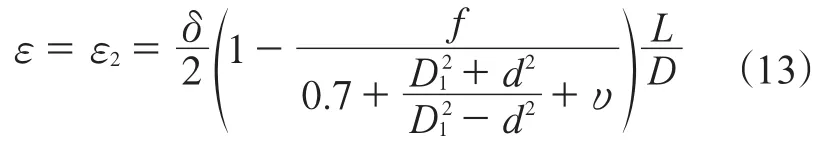
综上所述，转子体内孔表面压力与过盈量和弹性模量呈正比，与内孔直径呈反比；转子体变形主要受预热温度、几何尺寸和材料自身性质的影响。

2 结果与讨论

2.1 温度场分析

ANSYS软件中根据温度场性质不同，将热分析分为稳态热分析和瞬态热分析[8]。

瞬态热分析用于计算系统随时间变化的温度场及其他热参数。在瞬态传热过程中，系统的温度、热流率、热边界条件及内能不仅因位置不同而不同，而且随着时间变化而变化[9]。

根据能量守恒原理，用矩阵形式表示的通用瞬态热方程如下：

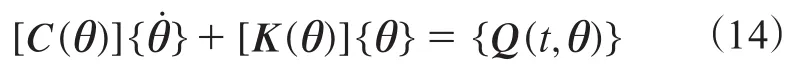
式中 [C]——比热矩阵，考虑系统内能的增加；

{θ}——节点温度向量；

[K]——热传导矩阵；

{Q}——节点热流率负载向量；

t——时间，s。

本研究的工艺条件为对转子体预热100 s，保温200 s，装配后冷却7 500 s。根据工艺条件选用瞬态热分析。

转子温度场云图如图3所示（转子装配后冷却7 500 s），转子温度测量点如图4所示，试验测得的装配后转子表面温度如表1所示。

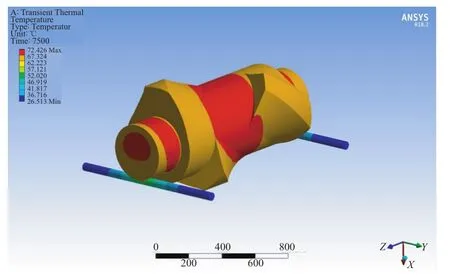
图3 转子温度场云图Fig.3 Nephogram of rotor temperature field

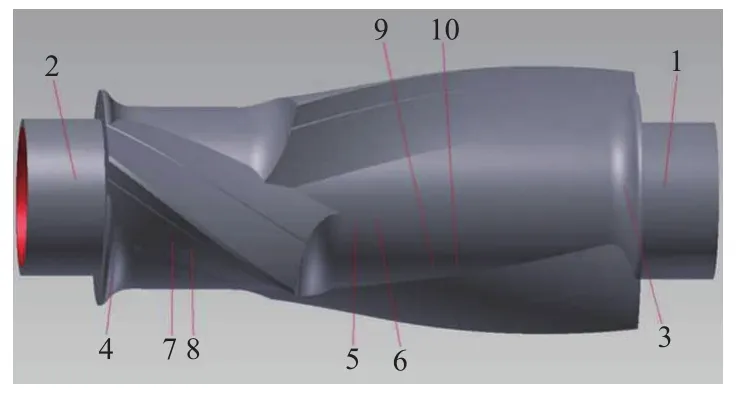
图4 转子温度测量点示意Fig.4 Diagram of rotor temperature measurement points

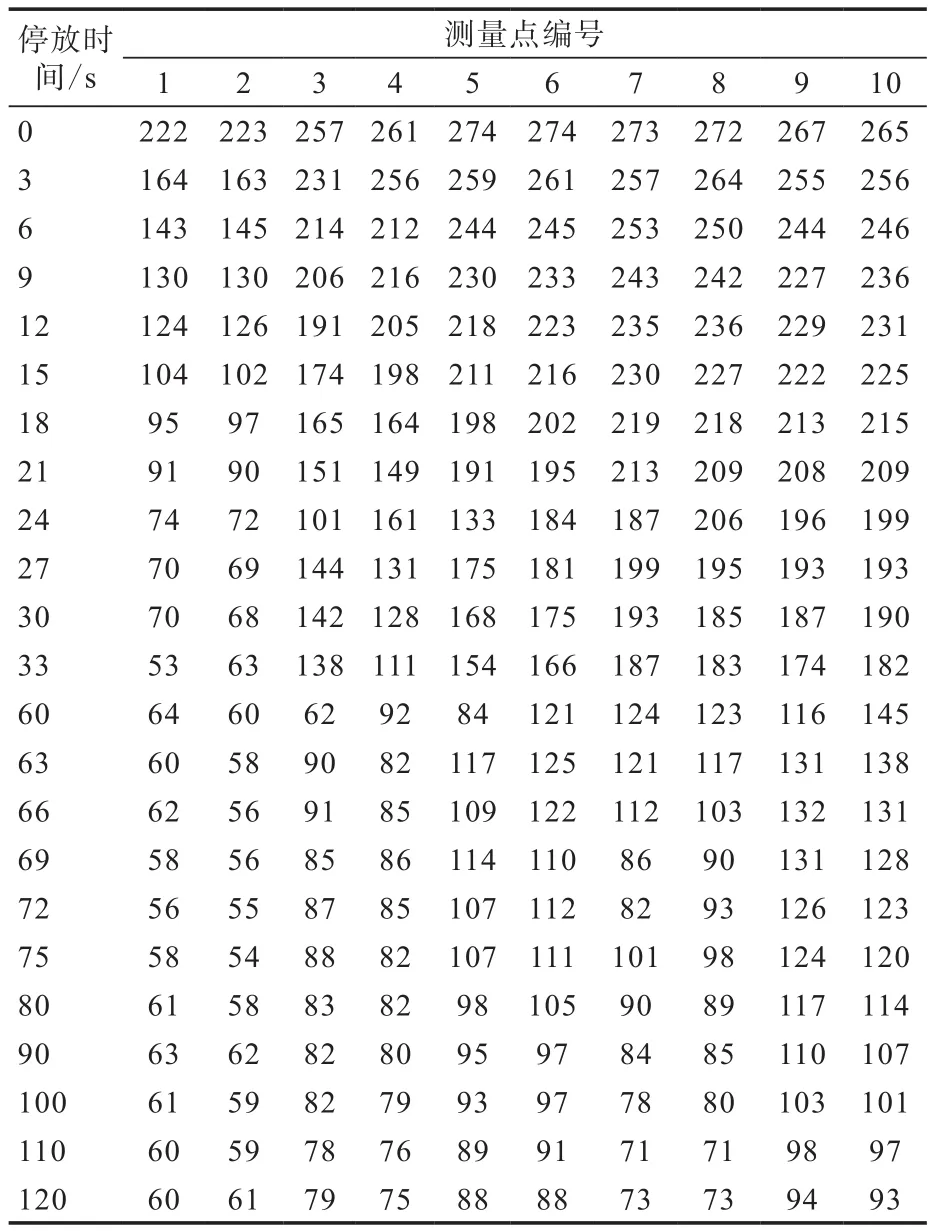
表1 装配后转子表面测量温度Tab.1 Surface measurement temperature of rotor after assembling ℃

对比图3与表1的数据可以看出，转子温度模拟结果与试验结果基本一致。

2.2 热变形分析

转子体热变形是导致转子体与转子芯轴之间产生缝隙的主要原因。提取温度场数据并作为边界条件导入结构分析器进行结构分析，根据实际受力情况设置边界条件，得到由热膨胀和冷收缩而引起的转子体热变形[10]。转子体与转子芯轴连接面的两端如果存在较大热变形，会导致密封不良，造成冷却水泄漏等问题，因此转子体两端位置是分析的重点。

过盈量为0.15，0.20和0.25 mm时转子体热变形分布分别如图5—7所示（转子装配后停放1 s）。从图5—7可以看出，转子体最大变形量分别为0.509 41，0.532 54和0.562 12 mm，最小变形量分别为0.102 13，0.129 85和0.158 78 mm。

从图5—7还可以看出，在不同过盈量时，转子体两端变形趋势和变形位置基本一致，但随着过盈量的增大，转子体变形量增大，这会改变密炼机的棱顶间隙，进而影响混炼效果。

图5 过盈量0.15 mm时转子体热变形分布Fig.5 Thermal deformation distribution of rotor body with interference of 0.15 mm

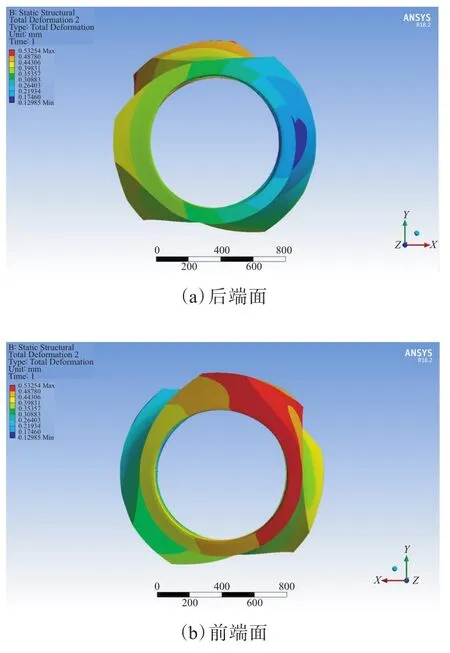
图6 过盈量0.20 mm时转子体热变形分布Fig.6 Thermal deformation distribution of rotor body with interference of 0.20 mm

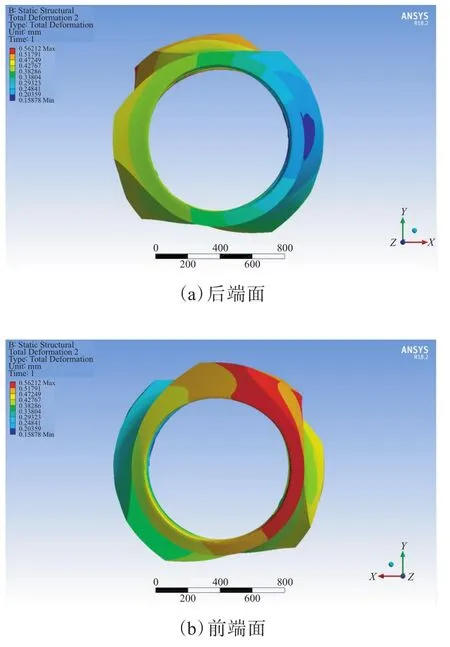
图7 过盈量0.25 mm时转子体热变形分布Fig.7 Thermal deformation distribution of rotor body with interference of 0.25 mm

2.3 热应力分析

温度改变时，物体由于外在约束以及内部各部分之间相互约束，不能完全自由胀缩而产生的应力称为热应力[11]。热应力过大会导致转子开裂和变形等问题。

过盈量为0.15，0.20和0.25 mm时转子体热应力分布分别如图8—10所示（转子装配后停放1 s）。从图8—10可以看出，转子体最大热应力分别为281.74，373.58和466.69 MPa。

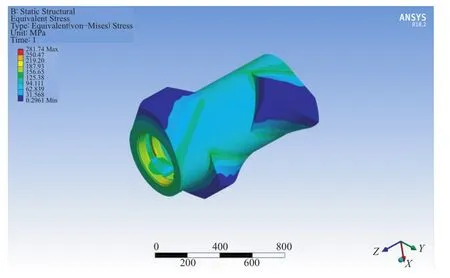
图8 过盈量0.15 mm时转子体热应力分布Fig.8 Thermal stress distribution of rotor body with interference of 0.15 mm

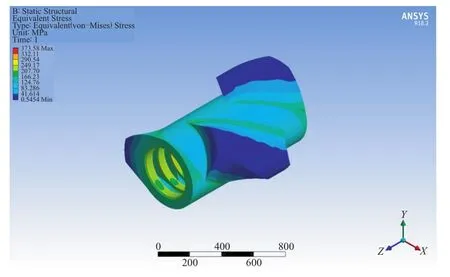
图9 过盈量0.20 mm时转子体热应力分布Fig.9 Thermal stress distribution of rotor body with interference of 0.20 mm

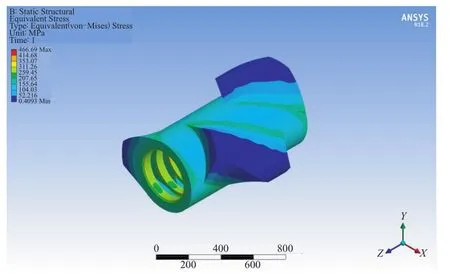
图10 过盈量0.25 mm时转子体热应力分布Fig.10 Thermal stress distribution of rotor body with interference of 0.25 mm

从图8—10还可以看出：转子体与转子芯轴接触面处热应力较大；转子体热应力与过盈量成正比，过盈量越大，热应力越大。当过盈量为0.15 mm时，转子体热应力未超过300 MPa，当过盈量为0.20和0.25 mm时，热应力超过300 MPa。

根据材料力学计算可知，当转子体热应力超过300 MPa时，转子结构体容易开裂，可见采用过盈量0.15 mm时，有利于防止转子体与转子芯轴密封不良而产生冷却水泄漏的问题。

3 结论

（1）利用有限元分析软件ANSYS对GK320型密炼机转子体与转子芯轴间3种不同过盈量下的温度场进行分析，得到不同过盈量下转子体热变形及热应力分布基本一致，随着过盈量的增大，转子体热应力增大，过盈量为0.15 mm时转子体与转子芯轴的密封满足要求。

（2）采用有限元仿真进行密炼机转子结构优化设计的方法是可行的，可为转子体与转子芯轴热装配的装配间隙和过盈量确定以及弱化应力集中提供参考。