强烈地震下农村砌体结构墙体重要性与抗震评定

2021-07-21林拥军杨敏润肖恬煦

建筑科学与工程学报 2021年4期

林拥军，周畅，杨敏润，肖恬煦，杨兵

(1. 西南交通大学土木工程学院，四川成都 610031； 2. 中国建筑西南设计研究院有限公司，四川成都 610041)

0 引言

砌体结构具有取材方便、造价便宜、耐久性和耐火性好的特点，在农村房屋结构中大量存在。由于砌体材料的脆性较大，使得砌体结构的抗震性能较差。已有震害研究表明，6.0级及以上强烈地震对农村砌体结构具有很大的破坏性。1975年海城地震、1976年唐山地震和2008年的汶川地震中，农村砌体结构房屋的破坏非常严重[1-3]。强烈地震通过地震波释放出能量，使地表产生剧烈运动和变形，具有随机突发、区域特性明显、破坏范围大和难以预测的特点。中国地处世界两大地震带(环太平洋地震带和欧亚地震带)之间，地震活动频繁，大多数地区都爆发过强烈地震。其中，很多地震重灾区发生在离震中较近的农村地区，因此，对农村房屋进行抗震评定是广大土木科技工作者首要解决的问题。笔者认为，对结构进行抗震评定应考虑结构构件的重要性问题。地震作用下，不同种类、不同部位的构件对结构整体的影响程度会有差异，如果某个构件的失效较容易导致整个结构的破坏，则该构件在结构中的作用也就相对重要，这便是构件的重要性问题[4-7]。

构件的重要性评价可分为定性评价法和定量评价法2类。定性评价主要根据工程经验对构件重要性进行区分，对复杂结构应用较为困难，一般仅适用于简单结构。在定量评价方面，荣海澄等[8]和Gharaibeh等[9]提出以结构构件抗力减小后所导致结构可靠度的降低程度来衡量构件的重要性，该方法不仅计算复杂而且应用十分困难。柳承茂等[10]认为构件的重要性与构件弹性刚度成正比，通过在构件主轴刚度方向施加单位平衡力系，并以构件在各方向的内力和作为构件的重要性指标，其合理性仍值得商榷。张雷明等[11]基于线弹性理论和能量流，以拆除构件后结构总应变能的变化程度来度量构件的重要性，该方法不仅计算繁琐、难于应用，而且未考虑结构的弹塑性特性。叶列平等[12]通过定义广义结构刚度，以拆除构件对广义结构刚度的影响程度作为该构件重要性评价指标，该指标物理概念较为清晰，但仅限于弹性结构系统。王功文[13]针对索杆张力结构，采用刚度折减法模拟构件损伤，并以构件损伤后结构自振频率的下降率作为构件的重要性评价指标，该方法不仅未考虑结构弹塑性特性，而且仅适用于索杆张力结构。Nafday[14]采用拆除构件法得到结构刚度矩阵行列式，并进行标准化，以完好结构的刚度矩阵行列式与拆除构件后结构的刚度矩阵行列式的比值作为构件的重要性评价指标，但结构刚度矩阵行列式的取值并没有明确的工程物理含义，难以体现结构构件在工程上的重要性。Agarwal等[15-16]和Pinto等[17]从图论的角度，将结构构件按连接能力划分为不同的结构簇，并分析结构簇的构形和结构失效模式，基于刚度矩阵行列式的概念提出了整体性指标和损伤程度指标,但仍然存在物理含义不明确的问题。

鉴于此，本文针对典型农村砌体结构遭遇强烈地震时的墙体重要性展开研究，提出墙体重要性系数的计算方法，分别采用静力和动力弹塑性方法分析墙体对结构抗震能力的影响，在砌体结构房屋的抗震评定中，引入墙体重要性系数，使农村砌体结构的抗震评定与维修加固更合理。

1 砌体结构墙体重要性的定义

1.1 墙体重要性系数

砌体结构在强烈地震所产生的水平作用力下，会受到竖向压力和水平剪力的联合作用。在受压承载力相同的情况下，墙体承受的压力越大，其失效概率也越大，重要性越高；在抗剪承载力相同的情况下，墙体承受的剪力越大，其失效概率也越大。从墙体失效对结构产生的破坏后果来讲，结构的安全等级越高，破坏后果越严重，该墙体的重要性越高。因此，砌体结构墙体的重要性与竖向压力、水平剪力及结构安全等级有关，其重要性系数可表示如下

γij=γ0+Δγij

(1)

(2)

式中：γij为第i层第j片墙体的重要性系数；γ0为与结构安全等级有关的墙体重要性系数,安全等级为一级取1.1，二级取1.0，三级取0.9[18]；Δγij为与竖向压力、水平剪力相关的墙体重要性系数；Nij为第i层第j片墙体底部所受的竖向压力；Vij为第i层第j片墙体底部所受的水平剪力；f(Nij)为第i层第j片墙体的受压重要性影响函数；g(Vij)为第i层第j片墙体的受剪重要性影响函数。

用aij和bij来代替f(Nij)和g(Vij)，则式(2)可表示为

Δγij=aijγN,ij+bijγV,ij

(3)

(4)

(5)

(6)

式中：aij为第i层第j片墙体抗压重要性影响系数；bij为第i层第j片墙体抗剪重要性影响系数；γN,ij为抗压重要性系数；γV,ij为抗剪重要性系数。

与结构安全等级相关的墙体重要性系数变化幅度为0.1，因此与竖向压力、水平剪力相关的墙体重要性系数Δγij的最大值为0.1，最小值为0，应对其进行标准化处理，使其分布于0～0.1之间，即

(7)

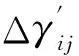
将Δγij标准化后，砌体结构墙体的重要性系数计算公式为

(8)

1.2 基于静力响应的抗剪重要性系数

静力响应是结构在静力作用下的反应，可以反映结构的静力性能。当水平地震作用一定时，结构顶部位移越小(或在结构顶部施加一定的位移时，其基底反力越大)，则结构抗侧刚度越大。根据构件拆除原理可知，如拆除构件后的剩余结构在水平作用力下所产生的结构顶部位移越大，表明该构件对结构抗震能力的贡献越大，其重要性程度越高。为避免局部构件拆除后引起结构的倒塌问题，需要在拆除构件顶部施加向上的竖向荷载。

结构的静力响应可采用静力弹塑性分析得到，通过在结构的顶部施加位移，可得到结构在该位移作用下的基底反力。此时，抗剪重要性系数γV,ij的计算公式为

(9)

式中：VS,ij为第i层第j片墙体拆除后剩余结构的基底剪力；VS,0为完整结构的基底剪力。

1.3 基于动力响应的抗剪重要性系数

动力响应是结构在动力作用下的反应，能反映结构的动力性能。结构的动力响应可采用动力弹塑性分析得到，若拆除构件后剩余结构在动力作用下的顶部位移越大，表明该构件对结构抗震能力的贡献越大，其重要性越大。与静力响应不同的是，动力响应可以反映结构多阶振型、动力特性及地震波持时等因素的影响。此时，抗剪重要性系数γV,ij的计算公式为

(10)

式中：dij为第i层第j片墙体拆除后剩余结构的顶部位移最大值；d0为完整结构的顶部位移最大值。

需要说明的是，基于静力响应的抗剪重要性系数采用静力弹塑性分析得到，而基于动力响应的抗剪重要性系数采用动力弹塑性分析得到。静力弹塑性分析主要考虑型荷载与结构一阶振型响应之间的关系，反映了地震峰值强度的影响，但不能分析地震频谱特性和持续时间的影响，而动力弹塑性分析反映了地震峰值强度、频谱特性和持续时间以及全部振型的影响。

2 农村砌体结构及有限元模型

2.1 典型农村砌体结构

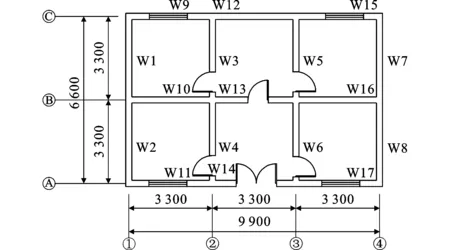
现有农村居民住房大多为1至3层3跨的砌体结构，其中2层3跨占比最大[2,6]。为此，本文以2层3跨砌体结构为例，进行强烈地震下的墙体重要性研究。楼(屋)面板为现浇钢筋混凝土板，混凝土强度等级为C25，保护层厚度20 mm，钢筋采用φ8@200，双层双向。墙体采用MU10烧结普通砖，M5混合砂浆砌筑，墙体厚度为240 mm，开间、进深和层高均为3.3 m,整个建筑长9.9 m，宽6.6 m，建筑平面及墙体编号如图1所示。为了解构造柱、圈梁设置对墙体重要性的影响，建立2个模型，未设置构造柱、圈梁的结构模型为Ms1，设置构造柱、圈梁的结构模型为Ms2。

2.2 砌体受压本构

根据砌体受压作用时的变形特点，国内外学者针对砌体受压本构模型开展了大量的试验和统计分析研究，提出的砌体受压本构关系曲线如下[19]

(11)

式中：σ为砌体轴心受压的压应力；fm为砌体抗压强度平均值；ε为砌体轴心受压的压应变；ε0为砌体轴心受压的峰值应变，取0.003 3。

2.3 结构有限元模型

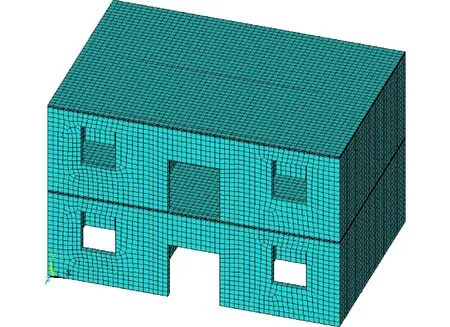
砌体是由块体和砂浆组成的一种复合脆性材料，根据这2种不同属性材料处理方式的不同，砌体结构的有限元模型有分离式模型和整体式模型2种[20]。分离式模型将砌体和砂浆分开建模，可以考虑2种材料的属性差异及块体与砂浆之间的应力重分布特征，适用于模拟砌体的损伤过程和破坏机理。整体式模型是将砂浆和块体的组合看成整体单元，不考虑块体和砂浆之间的属性差异，适用于结构整体分析。本文研究的是在整体效应下不同墙体的受力差异，采用整体式模型对结构进行有限元分析，墙体采用整体单元，构造柱、圈梁、楼板则采用弥散钢筋模型。地震作用下，砌体处于复杂受力状态，其抗剪、抗拉强度很低，容易进入非线性状态，并产生开裂。随着荷载的变化，结构局部的材料属性、截面属性的变化会对结构整体恢复力模型产生影响，需要对构件单元网格进行细化，降低构件剪切变形的影响，图2为完整结构的有限元模型。

3 基于静力响应的墙体重要性分析

采用构件拆除法分析不同墙体的相对重要性，即对拆除墙体后的剩余结构分别进行静力弹塑性分析、动力弹塑性性分析，并与完整结构相关参数进行对比，得出不同墙体对结构抗震能力的影响程度。

3.1 水平地震影响系数的影响

当水平地震作用于Ms1模型的x方向时，墙体抗剪重要性系数随水平地震影响系数的变化情况如图3所示。从图3(a)可以看出：结构内部墙体(W10)的抗剪重要性系数大于结构外部墙体(W11)，原因在于结构内部墙体不仅可以提供侧向刚度，还会减小y向的连接跨度，从而提高结构的整体性。从图3(b)可以看出：W10与W16墙体的抗剪重要性系数的变化规律并不相同，随水平地震影响系数的增加，处于受拉区的墙体W10的重要性系数先呈增大趋势，然后突然下降；墙体W16比W10的抗剪重要性系数大，原因在于W16墙体处于结构的受压区，而W10墙体处于结构的受拉区，在水平地震作用下，受拉区墙体的竖向压力减小，而受压区的墙体竖向压力增大，这会导致结构整体承载能力下降，墙体受压区的压应力和剪应力均大于受拉区墙体，其抗剪重要性也更高。从图3(c)可以看出，随水平地震影响系数的增加，受压区W8与W16墙体的重要性呈下降趋势，原因在于，随着地震作用的增大，墙体在压剪复合应力下会产生剪切滑移，砌体单元处于双向的压剪复合应力状态，使裂缝传递剪力的能力提高，结构刚度最后随受压区墙体的破坏突然下降，导致墙体的抗震能力出现下降。总体来讲，墙体的抗剪重要性随地震作用强度的变化较为复杂，随水平地震影响系数的增大，受压区墙体的抗剪重要性减小，而受拉区墙体的抗剪重要性增大。

3.2 构造柱、圈梁的影响

以Ms1，Ms2模型首层墙体W11为研究对象，分析构造柱、圈梁设置对墙体重要性的影响。不同构造柱设置下，墙体抗剪重要性系数随水平地震影响系数变化曲线如图4所示。从图4可以看出，随着水平地震影响系数的增大，墙体抗剪重要性呈先增大后减小的变化趋势。当地震作用强度较小时，设有构造柱、圈梁的约束墙体比未设置构造柱、圈梁墙体的抗剪重要性高，原因在于构造柱和圈梁的弱框架作用使墙体承受的压应力降低，在同等地震作用强度下，墙体开裂导致结构的刚度降低幅度较大。当水平地震影响系数较大时，有构造柱、圈梁的约束墙体比未设置构造柱、圈梁墙体的抗剪重要性低，这说明设置构造柱、圈梁会增强砌体结构整体性，从而使得拆除墙体W11后的剩余结构整体刚度变化较小。

3.3 墙体位置的影响

以模型Ms1为例，分析墙体平面位置、竖向位置对抗剪重要性的影响。

3.3.1 平面位置的影响

以底层受拉区W2，W4，W9墙体和受压区W6，W7，W17墙体为例进行分析，图5为不同平面位置墙体抗剪重要性系数随地震影响系数的变化曲线。从图5(a)可以看出：当水平地震影响系数小于0.5时，墙体W4的抗剪重要性大于W9的抗剪重要性；W2与W4的抗侧刚度相同，但墙体的抗剪重要性却相差较大，这表明墙体的抗剪重要性不仅与墙体自身的抗侧刚度有关，还受到墙体在结构中的拓扑关系及受力状态的影响；墙体W2和W9处于结构的周边，其失效对结构整体性的影响相对较小，它们的抗剪重要性也相对较小；墙体W4位于结构的内部，与之连接的墙体较多，墙体失效对结构的整体性影响较大，其抗剪重要性较大。从图5(b)中可以看出：虽然墙体W7的抗侧刚度小于墙体W17的抗侧刚度，对结构整体性的影响也不及墙体W6，但其抗剪重要性系数却最大，原因在于受压区外侧的墙体在地震作用下受竖向压力和弯矩影响较大，其刚度退化比内侧墙体大，墙体失效引起结构整体刚度的变化也越大。

3.3.2 竖向位置的影响

图6为不同竖向位置受拉区墙体W4，W10和受压区墙体W8，W17抗剪重要性系数随地震影响系数的变化情况。从图6可以看出，同一平面位置的墙体，从下而上，内部墙体的抗剪重要性增大，周边墙体的抗剪重要性减小。

4 基于动力响应的墙体重要性分析

4.1 地震波的选取

结构动力弹塑性分析中，地震波的选择很重要，由于震源机制、传播介质以及地质构造的复杂性，《建筑抗震设计规范》[21]建议：选择地震波时主要考虑地震动强度、地震动频谱特性和地震动持续时间；地震波可采用场地实际强震记录、典型的强震记录和人工模拟地震波。

鉴于实际强震记录和建筑物所在场地的基本烈度并不对应，这就需要根据抗震设防目标要求对地震加速度峰值进行调整，即

(12)

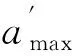
为考虑地震动频谱特性、持续时间的影响，按场地特征周期Tg分别为0.3，0.4，0.5 s，选定3条地震波，分别为SeW1，SeW2和SeW3，如图7所示；持续时间t为20，30，40 s的地震波分别为SeW5，SeW6和SeW7，如图8所示。

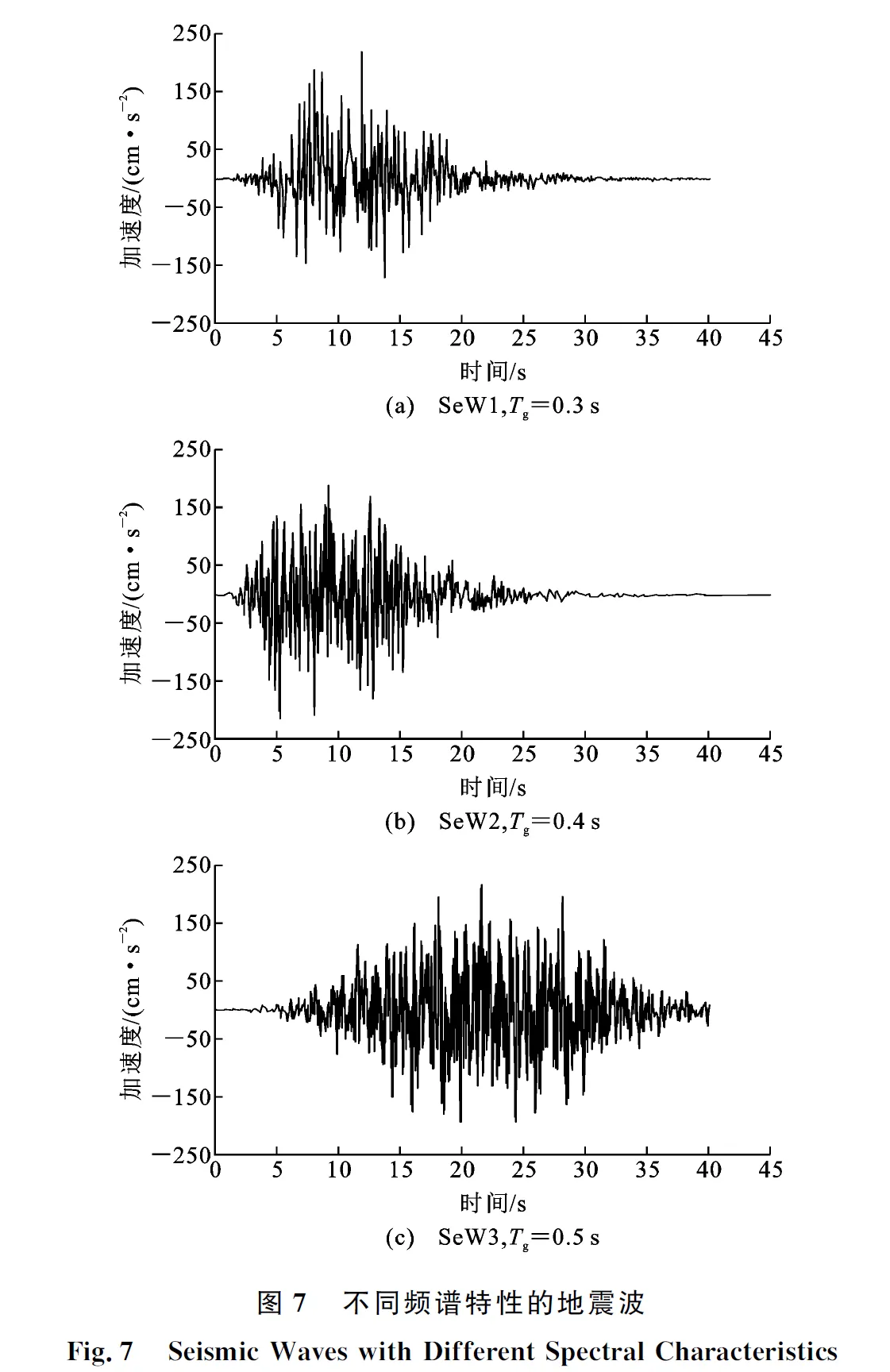
4.2 地震波频谱特性的影响

以模型Ms2的W11墙体为例，研究地震动频谱特性、地震动持时对墙体抗剪重要性的影响。

地震波的频谱特性包含卓越周期、强度包线参数，墙体的抗剪重要性系数如表1所示。不同频谱特性地震波下，动力弹塑性分析得的结构顶点位移Ux时程曲线如图9所示。结果表明，不同频谱特性地震波下，墙体的抗剪重要性系数有较大差异，与加速度反应谱0～0.1 s谱值分布基本一致。

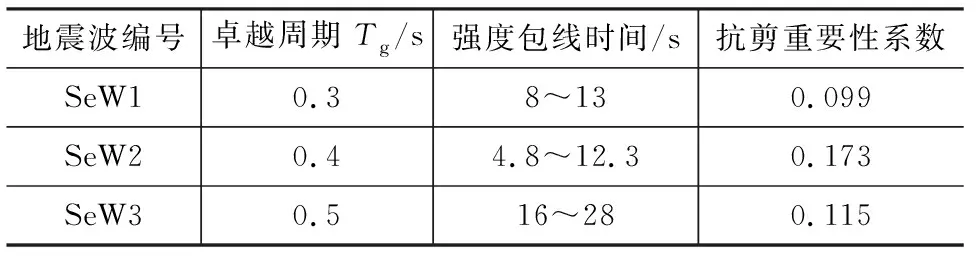
表1 地震波的频谱特性参数与墙体抗剪重要性系数Tab.1 Spectral Characteristic Parameters of Seismic Waves and Importance Coefficient of Wall Shear Resistance

4.3 地震波持时的影响

不同持时地震波的特征参数与墙体的抗剪重要性系数如表2所示。不同持时地震波下，动力弹塑性分析得到的结构顶点位移时程曲线如图10所示。分析结果表明，砌体结构进入非线性阶段之后，结构顶点的最大位移与墙体的抗剪重要性系数一致，结构最大响应与结构进入塑性阶段的塑性持时有关，而塑性持时一般在地震动峰值附近。

表2 不同持时地震波特征参数与墙体抗剪重要性系数Tab.2 Characteristic Parameters of Seismic Waves with Different Duration and Importance Coefficient of Wall Shear Resistance

5 基于墙体重要性的抗震评估

基于静力响应与动力响应的墙体重要性分析表明，地震峰值强度、频谱特性和持续时间等动力参数对墙体重要性系数均有一定的影响，但地震动加速度峰值是墙体抗剪重要度最主要的影响因素，抗震评估时可以采用基于静力响应的墙体重要性系数进行抗震评估。

5.1 墙段抗震能力指数

水平地震作用下墙体的剪力会按质量和刚度进行分配，刚度、质量越大的墙体分配的地震剪力越大，其对砌体结构抗震能力的贡献越大，说明该墙体的重要性越高。因此，砌体结构抗震评定时需考虑墙体抗震重要性的影响。

根据《建筑抗震鉴定标准》[22]，在对A类砌体结构进行第二级抗震鉴定时，应将墙段综合抗震能力指数按如下公式进行计算

(13)

式中：βc,ij为第i层第j墙段综合抗震能力指数；βij为第i层第j墙段抗震能力指数；Aij为第i层第j墙段在1/2层高处的净截面面积；Ab,ij为第i层第j墙段计及楼盖刚度影响的从属面积；λ为地震烈度影响系数；ξ0i为第i层第j片纵向或横向抗震墙的基准面积率；Ψ1为体系影响系数；Ψ2为局部影响系数。

对于B类砌体结构，为进行墙体抗震能力比较，定义墙体的抗震能力验算指数如下

βv,ij=fvEA/[γRa(1+γij)V]

(14)

fvE=ζNfv

(15)

式中：βv,ij为第i层第j片墙体抗震能力验算指数；fvE为砌体沿阶梯形截面破坏的抗震抗剪强度设计值；fv为非抗震设计的砌体抗剪强度设计值；ζN为砌体抗震抗剪强度的正应力影响系数；γRa为抗震鉴定的承载力调整系数；A为墙体横截面面积；V为墙体剪力设计值。

当βc,ij或βv,ij大于等于1.0时，评定为抗震能力验算满足要求，反之，评定为抗震能力验算不满足要求。

5.2 抗震评定实例

5.2.1 工程概况

该工程为2层砌体结构房屋，设防烈度为7度，设计基本地震加速度为0.1g(g为重力加速度)，设计地震分组为第一组，场地类别为Ⅱ类，层高为3.3 m，建筑平面如图1所示。楼(屋)面板采用现浇钢筋混凝土板，混凝土强度等级为C25，钢筋采用φ8@200，双层双向。墙体采用烧结普通砖，强度等级为MU10，砂浆强度等级为M5，基于静力响应的墙体重要性系数如图11所示。

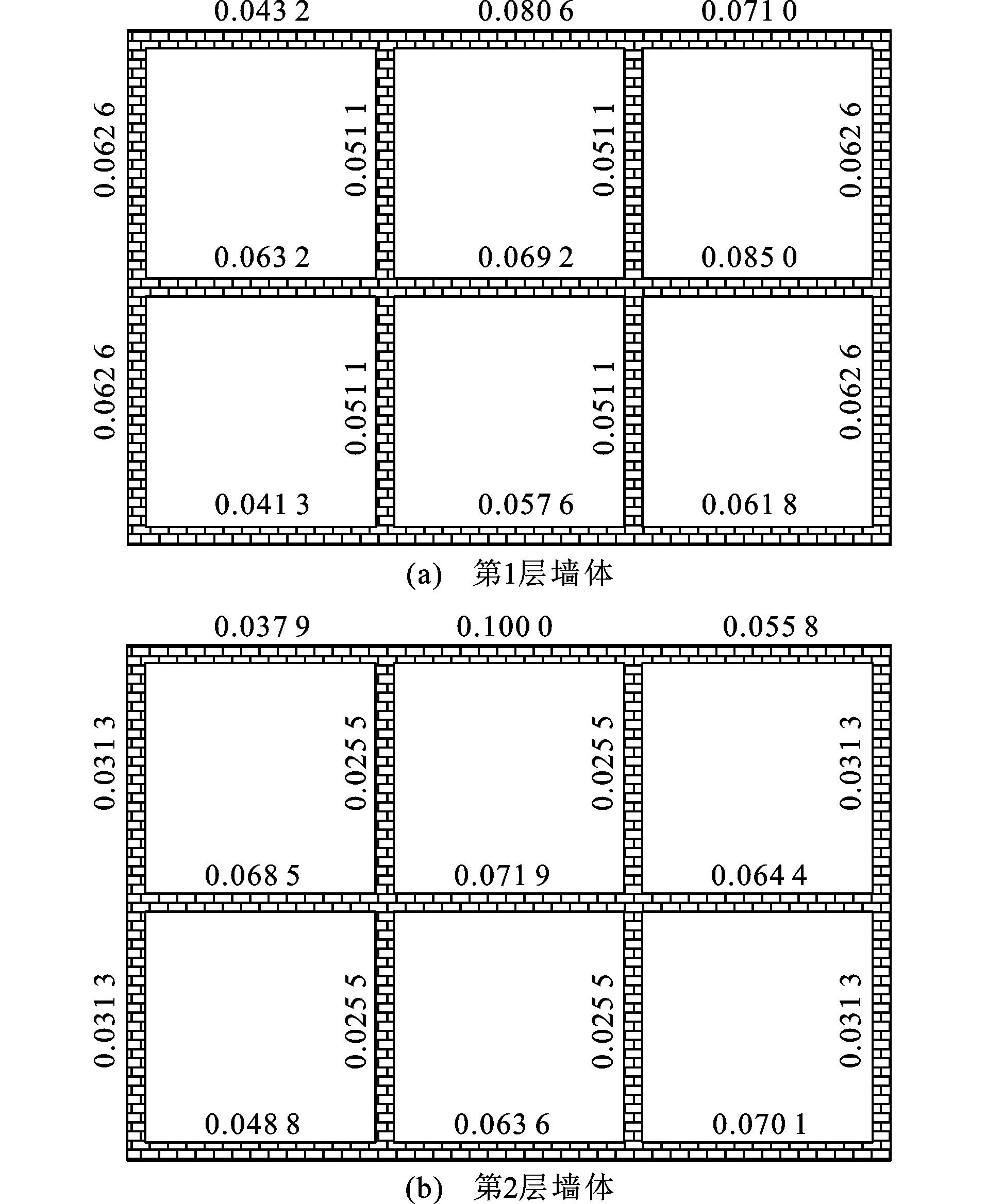
5.2.2 墙段综合抗震能力指数计算

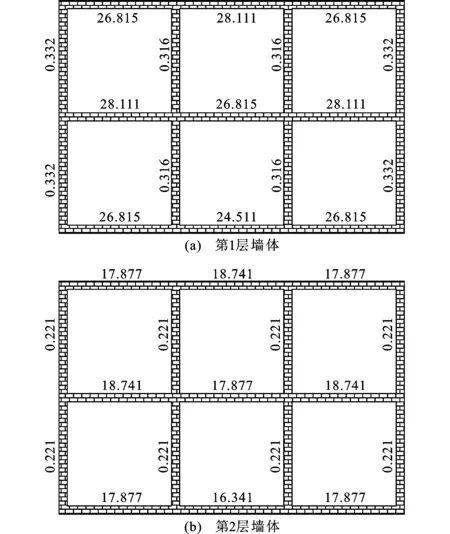
按A类砌体房屋进行第一级鉴定不满足要求，根据公式(13)计算的墙段抗震能力指数进行第二级评定。经过计算得到2层墙体的综合抗震能力指数如图12所示，可以看出，所有墙体的综合抗震能力指数均大于1，该砌体房屋满足第二级鉴定要求。

5.2.3 墙段抗震能力验算指数计算

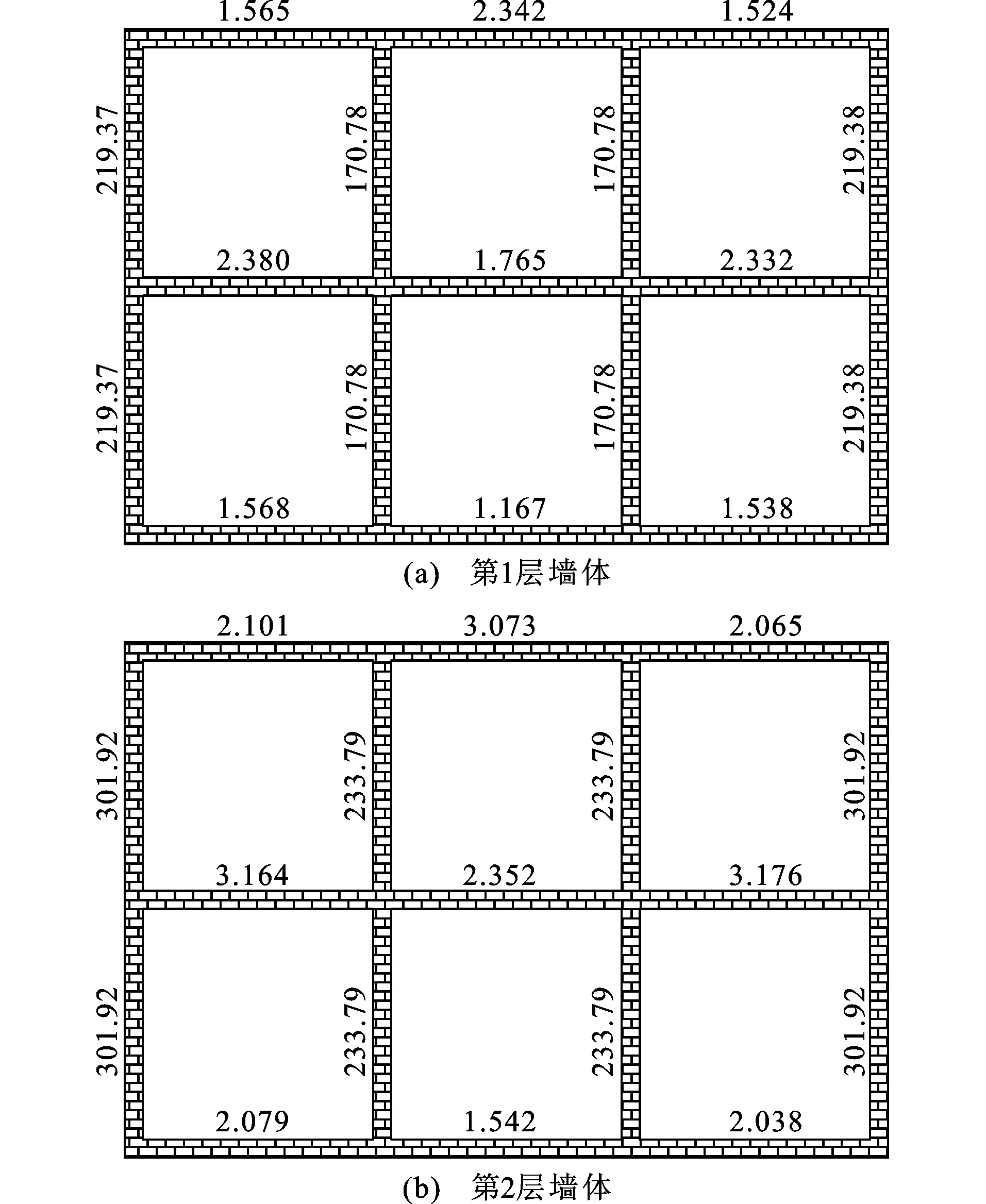
按B类砌体，采用设防烈度进行抗震验算，水平地震影响系数最大值取0.23，按《建筑抗震设计规范》[21]的地震反应谱计算的水平地震影响系数为0.217，按底部剪力法求得各墙体的剪力设计值如图13所示。按B类砌体房屋进行第一级鉴定不满足要求，根据公式(14)，(15)计算的墙段抗震能力验算指数进行抗震能力验算，墙体抗震能力指数均大于1，如图14所示，抗震能力评定为满足要求。