天津地区微水试验求取含水层渗透系数的应用

2021-07-21肖传宁刘承磊李连营孙怀军

水利与建筑工程学报 2021年3期

肖传宁，刘承磊，李连营，孙怀军

(天津市勘察设计院集团有限公司，天津 300000)

含水层的渗透系数是反映岩土体渗透性的重要参数，也是水文地质及工程地质勘察工作中的关键参数[1-2]。目前，国内测定含水层渗透系数的主要手段为抽水试验，但其存在需要大量的人力物力，耗费较长时间等缺点[3]。同时，对于渗透性较弱、储水性较差的含水层，做抽水试验非常困难[4]。微水试验是利用某种方式使井(孔)中水位在一瞬时发生微小变化，并通过观测井(孔)中水位随时间的变化过程确定含水层水文地质参数的现场试验方法[5]。与抽水试验相比，该方法具有操作简便、试验周期短及对含水层扰动较低等优点[6-7]。国外对微水试验的研究开展得较早，研究成果较多，在理论和求解方法方面已较为成熟，常用的有Hvorslev模型、Bouwer&Rice模型和Cooper模型等，国内的研究主要在国外已有的研究基础上进行且在工程实践中应用较少[8-9]。林广宇等[10]通过对比微水试验、抽水试验及室内土工试验的结果，研究了微水试验求取含水层渗透系数的可靠性，本文是在其基础上的进一步应用。

本文以天津市某场地潜水含水层和微承压含水层的微水试验资料为基础，利用Aquifer Test中Slug Test模块求解，并与抽水试验计算结果对比，分析了微水试验技术在天津地区测定水文地质参数的精度及适用性，为该技术的实践及推广提供一定的参考依据。Aquifer Test软件具有简便、友好、直观的使用界面，并具有优良的可视化效果，其中的Slug test模块是分析处理微水试验数据的常用工具[11]。

1 工程概况及试验方案

1.1 工程概况

试验场地位于天津市河东区某地块内，拟建商务办公楼2座、商业楼5座及地下车库。地下车库整体4层，埋深约21.0 m。场地内为施工临建用地、堆土场、钢筋加工区及施工临时道路等；场地西侧为项目二期工程、南侧为三期A地块工程、东侧为六纬路、北侧为八经路，其中二期工程为超高层公寓楼即将竣工，三期A地块正在进行西半部分主体施工，六纬路、八经路均为现状道路，交通繁忙。工程概况如图1所示。

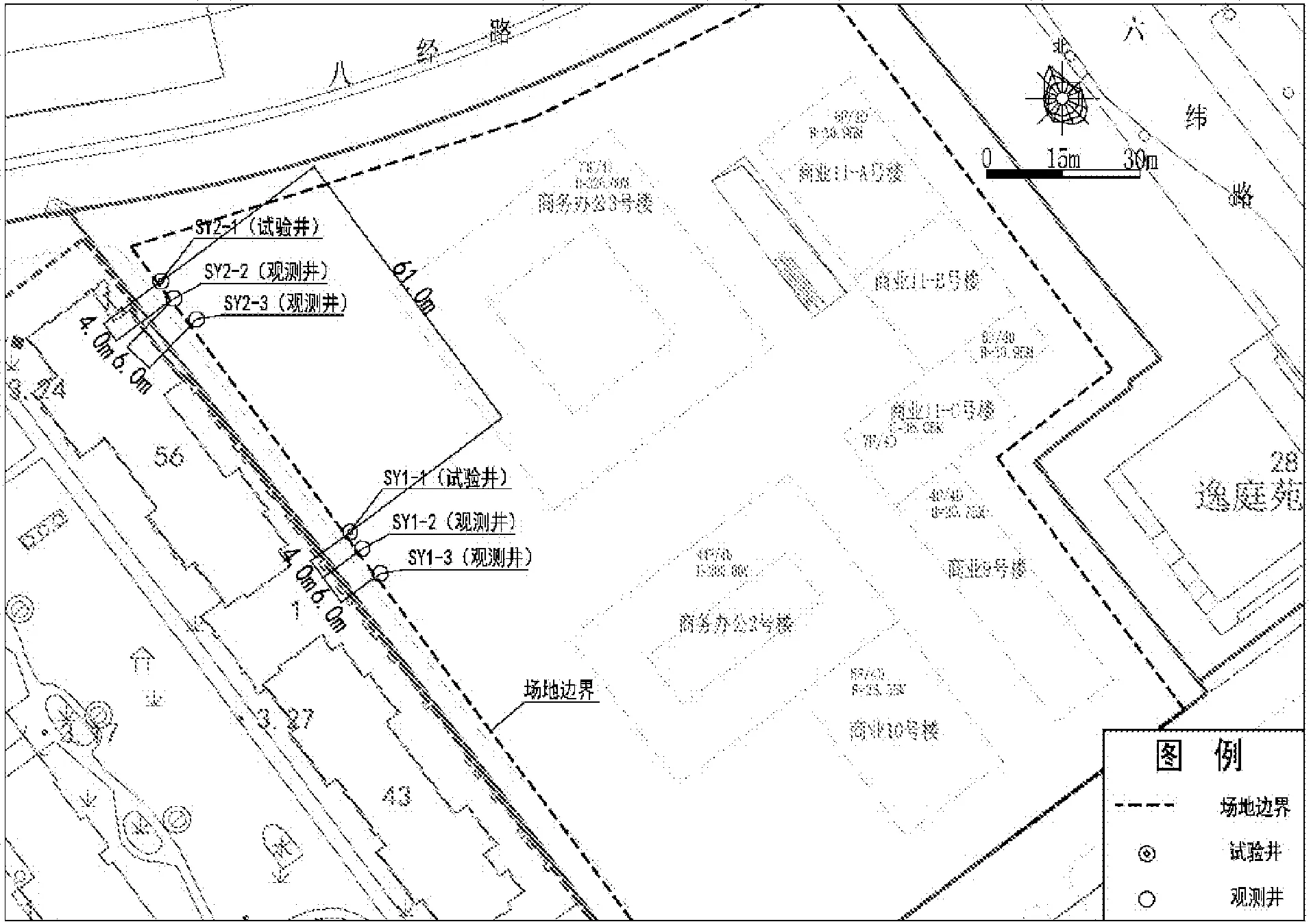
图1 工程概况及井位布置图

1.2 水文地质条件

根据工程勘察结果，场地埋深28.00 m深度范围内的地层主要为人工堆积层及第四纪陆相、海相、沼泽相沉积层。按地层岩性及成因可自上而下划分为6个大层，进一步划分为10个亚层，根据岩性分布、室内渗透试验结果综合分析可分为潜水含水层、相对隔水层及承压含水层。场地地层分布特征如表1所示。

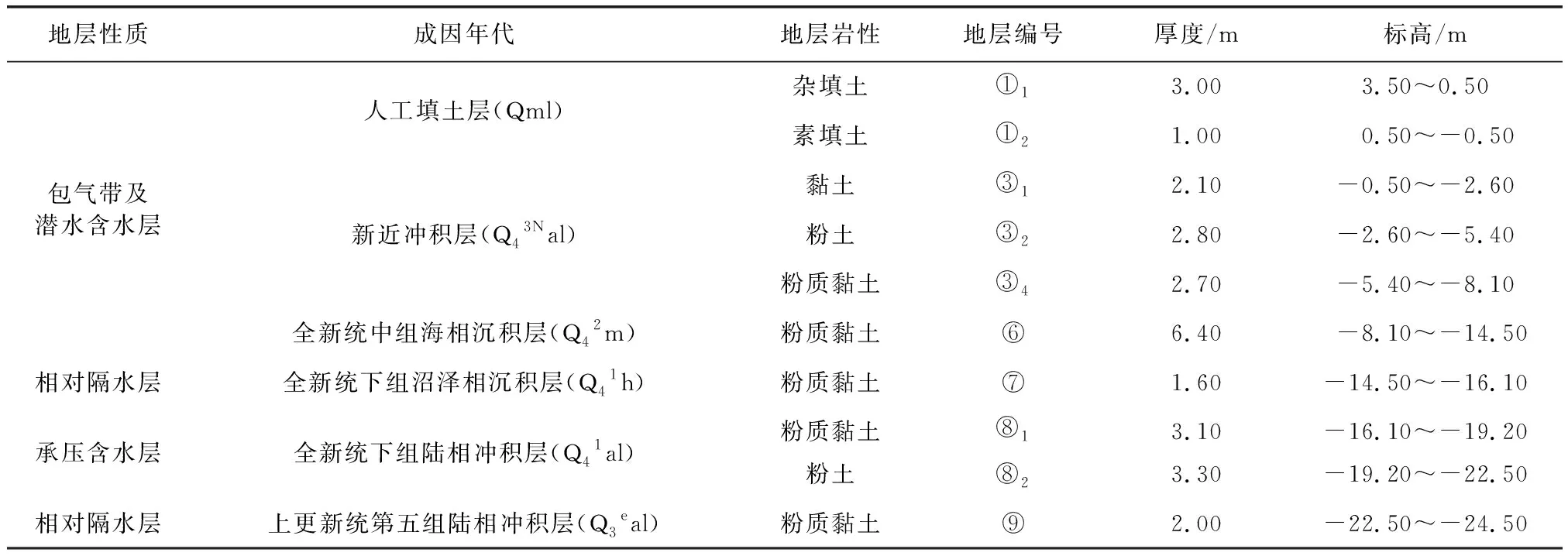
表1 场地地层分布情况

场地潜水天然动态类型属渗入-蒸发径流型，主要接受大气降水入渗和地表水体渗漏补给，排泄方式主要为蒸发、地下水侧向径流和垂向越流。地下水总体流向为自北西向南东，水位变幅0.5 m～1.0 m。承压水天然动态类型属渗入-径流型，以越流补给、地下水侧向径流和“天窗”渗漏补给为主，排泄方式主要为侧向径流和越流。

1.3 微水试验情况

本次在场地内布设6口试验井(SY1-1、SY1-2、SY1-3、SY2-1、SY2-2、SY2-3)，其中，SY1-1、SY1-2、SY1-3为潜水含水层完整井，SY2-1、SY2-2、SY2-3为承压含水层完整井。针对场地潜水含水层及承压含水层的微水试验分别在SY1-1、SY2-1中进行1次，水位测量采用Micro Diver自动水位记录仪监测。同时，为分析微水试验的精度，在潜水含水层及承压含水层分别进行了1次带2个观测井的抽水试验，试验井SY1-2、SY1-3为潜水水位观测井，SY2-2、SY2-3为承压水水位观测井。抽水试验在完成微水试验且在水位完全恢复后进行。井位布置情况如图1所示，井身结构参数见表2。

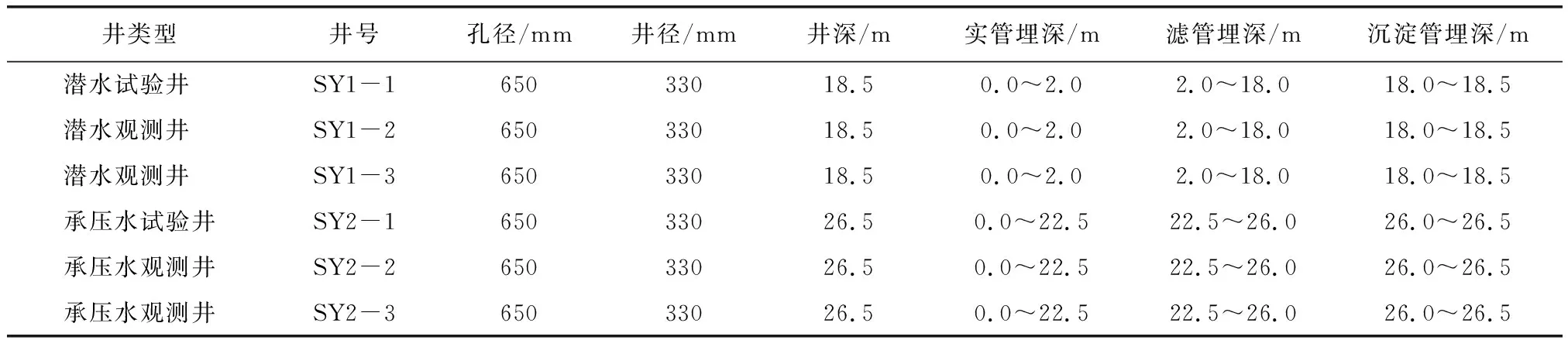
表2 井身结构参数表

2 微水试验基本原理

目前国内外提出的微水试验求解模型多达50种，这些模型中Hvorslev模型、Cooper模型及Bouwer&Rice模型较为常用。

2.1 Hvorslev模型

Hvorslev[12]在20世纪50年代发展建立的Hvorslev模型是一种适用于承压含水层完整井的求解模型，其忽略了含水层的弹性释水过程。

Hvorslev模型的表达方式如下，一般采用直线图解法求解：

(1)

(2)

式中：H0为初始水头变化；H(t)为随时间的水头变化；t为时间；R为微水试验影响半径；rw为井管半径；rc为钻孔套管半径；K为含水层渗透系数；M为承压含水层厚度；T0为基本时间间隔，即变化的水位降深与初始水位降深之比为0.37时所对应的时间。

2.2 Cooper模型

20世纪60年代，Cooper等[13]建立了一种适用于承压含水层完整井的Cooper模型求解方法，考虑了含水层的弹性释水效应。

Cooper等给出了如下形式的解析解，利用标准曲线配线法求参数：

(3)

f(u,α)=[uJ0(u)-2αJ1(u)]2+[uY0(u)-2αY1(u)]2

(4)

(5)

式中：α为无量纲释水系数；β为无量纲惯性参数；J0(u)为第一类零阶Bessel函数；J1(u)为第一类一阶Bessel函数；Y0(u)为第二类零阶Bessel函数；Y1(u)为第二类一阶Bessel函数。

2.3 Bouwer&Rice模型

Bouwer&Rice模型是由Bouwer等[14]建立发展的，其适用于潜水含水层，忽略含水层弹性释水效应。

H.Bouwer等给出了如下形式的解析解，一般采用直线图解法求解：

(6)

式中：re为滤管半径；L为含水层中滤管的长度。

对于完整井，Bouwer 和Rice给出了影响半径R的计算方式如下：

(7)

式中：b为滤管底部至含水层顶部的长度；h为静止状态下潜水含水层厚度；L为含水层中滤管的长度；A、B、C均为L/re的函数。

3 微水试验数据分析

3.1 微水试验计算结果

对潜水含水层试验井SY1-1、承压含水层试验井SY2-1各进行1次降水位微水试验，分别记录每次提水后水位随时间的恢复数据，利用上述数据分别采用适当的模型方法求解含水层渗透系数。

潜水含水层试验井SY1-1的静止水位为0.87 m，初始时刻最大水位降深约为0.30 m，试验周期约为75 min，其水位降深变化曲线如图2所示。

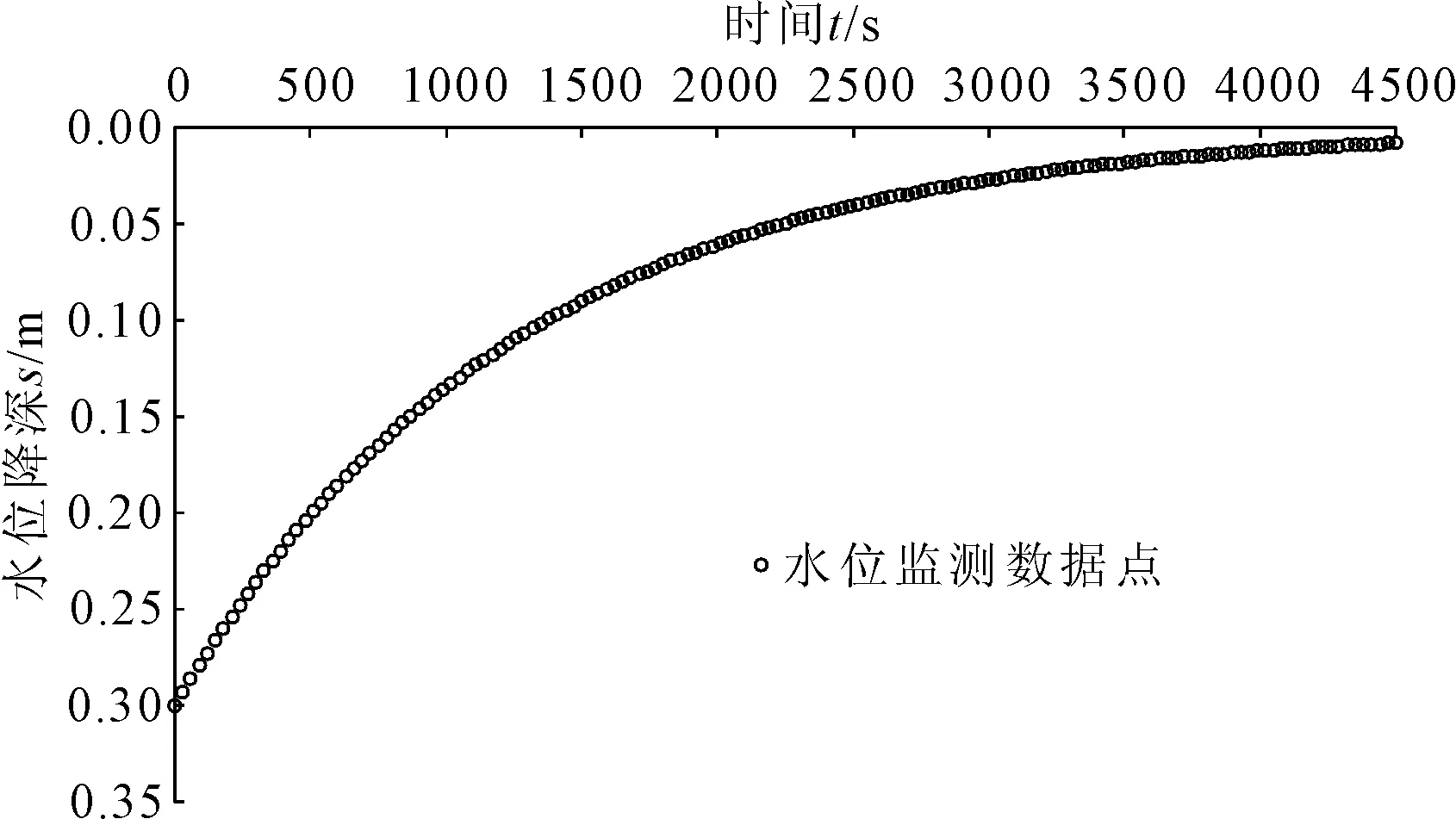
图2 潜水含水层微水试验水位降深随时间变化过程

潜水含水层采用Bouwer&Rice模型求解，利用Aquifer Test中Slug Test模块的配线过程如图3所示，求得场地潜水含水层渗透系数为0.209 m/d。

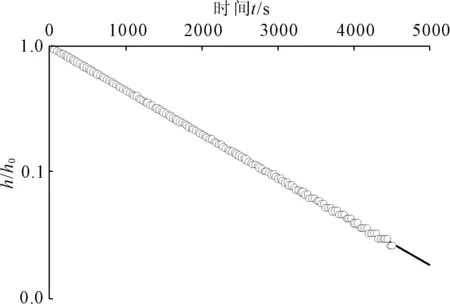
图3 潜水含水层微水试验Bouwer&Rice模型h/h0-t曲线

承压含水层试验井SY2-1的静止水位为-2.37 m，初始时刻的最大水位降深约为0.64 m，试验周期为10 min，水位降深变化曲线如图4所示。

图4 承压含水层微水试验水位降深随时间变化过程

承压含水层采用Hvorslev模型和Cooper模型求解，同样利用Aquifer Test中Slug Test模块的配线过程如图5、图6所示，求得场地承压含水层渗透系数分别为3.350 m/d、5.030 m/d。

图5 承压含水层微水试验Hvorslev模型h/h0-t曲线

3.2 数据分析

为对比微水试验结果的准确性，在不同含水层同一井中各进行1次带2个观测井的定流量抽水试验，并引用“相对偏差”的概念量化两种方法计算结果的差异，相对偏差为两种计算结果差与和之比的绝对值。潜水含水层抽水试验稳定抽水量约为25.34 m3/d，抽水井SY1-1最大水位降深为5.73 m，观测井SY1-2、SY1-3最大水位降深分别为2.63 m、1.53 m，抽水时长约为46 h。承压含水层抽水试验稳定抽水量约为87.41 m3/d，抽水井SY2-1最大水位降深为6.06 m，观测井SY2-2、SY2-3最大水位降深分别为3.01 m、1.91 m，抽水时长约为45 h。潜水含水层及承压含水层均采用Dupuit稳定流公式计算渗透系数，结果如表3所示。

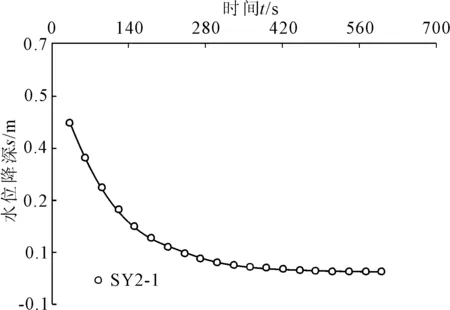
图6 承压含水层微水试验Cooper模型s-t曲线

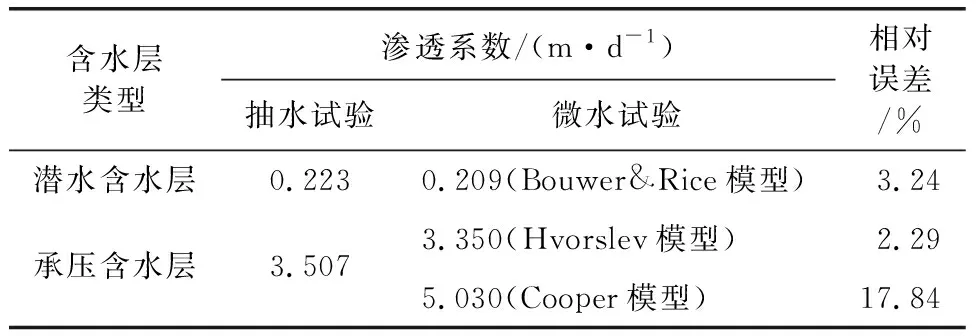
表3 抽水试验、微水试验渗透系数统计结果

由表3可以看出，潜水含水层微水试验Bouwer&Rice模型计算结果较抽水试验偏小，相对误差为3.24%。承压含水层微水试验Hvorslev模型计算结果较抽水试验偏小，相对误差为2.29%，Cooper模型计算结果较抽水试验偏大，相对误差为17.84%。

潜水含水层微水试验的试验井SY1-1中最大水位变化为0.30 m，承压含水层微水试验的试验井SY2-1中最大水位变化为0.64 m，水位变化远小于抽水试验的试验井水位变化值5.73 m、6.06 m。潜水含水层、承压含水层微水试验的试验周期分别为75 min、10 min，相较于抽水试验周期46 h、45 h较小。同时，潜水含水层、承压含水层微水试验均未对周边观测井中的水位产生影响。