内孤立波与平顶海山作用的能量耗散实验研究*

郭钰林 孟 静 徐 昱贾 村 刘 娟 陈 旭 于宇君

内孤立波与平顶海山作用的能量耗散实验研究*

郭钰林1孟 静4徐 昱5①贾 村2刘 娟3陈 旭1于宇君1

(1. 中国海洋大学物理海洋教育部重点实验室 青岛 266003; 2. 自然资源部第三海洋研究所海洋动力研究室 厦门 361005; 3. 北京应用气象研究所 北京 100029; 4. 中国海洋大学海洋与大气学院 青岛 266100; 5. 中国海洋大学工程学院 青岛 266100)

内波破碎引起的能量耗散和混合是海洋内部的重要物理过程。通过在二维内波水槽进行实验室实验, 分析内波与地形的作用, 探究内孤立波与平顶海山地形作用时波要素、能量以及湍耗散率的时空变化。本实验利用重力塌陷法在两层流体中制造第一模态内孤立波, 通过粒子图像测速技术(particle image velocimetry, PIV)获得内孤立波与地形作用时的流场结构, 定量分析整个作用过程。结果表明, 地形会改变波形甚至引起破碎, 内波与地形作用时, 振幅和能量密度会在内孤立波爬坡时迅速增大, 在地形前缘产生强烈能量耗散。入射波的能量与塌陷高度呈二次函数关系, 透射波能量随地形升高减小, 反射波能量随地形升高增大。地形前缘局地湍耗散率极值时间序列在部分实验中呈双峰结构, 对应内孤立波界面处剪切加强引起湍流耗散和波后缘翻转破碎。破碎引起的地形前缘区域平均湍耗散率量级在10-5m2/s3, 局地湍耗散率极值与入射波振幅呈指数关系, 所有实验中局地湍耗散率的最大值接近10-3m2/s3量级。

内孤立波破碎; 能量耗散; 湍耗散; 粒子图像测速

内波广泛分布于各个大洋和边缘海域, 是海洋中的普遍现象(Garrett, 1979; Jackson, 2007; Gerkema, 2008)。内孤立波是内波的一种, 它能够在生成后传播较长的距离并保持波形、能量等特性基本不变(Grimshaw, 1998; Jackson, 2007; Grimshaw, 2010)。它的最大振幅出现在海洋内部, 伴随着较强的剪切和垂向流动, 对海洋内部的混合、营养盐等物质输运以及海底沉积物再悬浮具有重要影响(Osborne, 1980; Reeder, 2011)。正压潮经过变化地形生成内潮, 在内潮传播过程中, 受其他因素影响, 非线性和色散性达到平衡演变成内孤立波。内孤立波在长距离传播过程中与海底地形相互作用, 并最终在陆架陆坡区消亡。例如中国南海北部的陆架陆坡处(Orr, 2003; Yang, 2009; Cai, 2012)和东沙环礁附近(Zhao, 2006; Bai, 2017)、安达曼海域(Shimizu, 2017; Raju, 2019)、俄勒冈州大陆架(Trevorrow, 1998; Moum, 2003, 2007)、墨西拿海峡(Droghei, 2016; La Forgia, 2018)、加利福尼亚内陆架(Colosi, 2018)。在与海脊地形和陆架陆坡地形相互作用时, 内孤立波界面处剪切加强, 能量耗散增强, 对流不稳定和剪切不稳定等机制引起内波破碎, 发生强烈混合和能量的损失(Orr, 2003; Vlasenko, 2002; Bai, 2017)。内波的能量耗散是海洋中能量级串的重要环节, 研究内孤立波与地形相互作用时的能量分配与耗散对于理解这一过程有重要意义。

在内孤立波与陆架陆坡相互作用的研究中, Orr等(2003)通过在南海北部陆坡区的走航观测捕捉到一组内孤立波的浅化过程, 观察到其波形发生极性转化。在16.5 km的传播过程中, 波列的总能量呈指数衰减, 其能量衰减系数为0.063 km–1。南海东沙环礁南部上层水的湍耗散率和跨密度面混合率, 在内孤立波经过时增大三个量级(Xu, 2012)。Moum等(2003)在俄勒冈州大陆架处观测到内孤立波, 其界面处的耗散率(Moum, 1995)量级在10–8—10–5m2/s3之间, 且波后缘的耗散率要大于前缘。该耗散强度, 大于内潮在Kaena Ridge处与地形作用破碎引起的耗散(10–6—10–7m2/s3)(Klymak, 2008); 略小于内潮经过Hawaii Ridge引起破碎得到的湍耗散率(10–-8—10–4m2/s3)(Klymak, 2012); 与New York Bight海底边界层的湍耗散率(10–6—10–5m2/s3)相当(Doron, 2001)。Vlasenko等(2002)通过数值实验讨论了内孤立波在安达曼海和苏禄海陆坡处的浅化传播过程。并在三维数值模拟实验中发现, 横向的地形变化会使内孤立波发生折射, 导致波面能量的横向再分配, 能量的聚焦使局部地区破碎发生的更快(Vlasenko, 2007)。

内孤立波与东沙环礁处特殊的海底地形相互作用, 会发生反射、折射、绕射、透射等现象。由于该区域单个反射波的能量较小, 最大值也仅为入射波能量的2%, 所以其反射波很难被卫星图像捕捉(Bai, 2017); 地形附近海水南深北浅, 波在此处会发生折射; 在绕射过程中, 波会被东沙环礁分成南北两支, 绕射后的两支波能否重新连接, 主要依赖于绕射前波的形状(Jia, 2018)。传播到该区域的内孤立波, 无论是透射还是反射, 都与该区域的层结结构和背景流相关 (Davis, 2017)。

实验室实验是内波研究的重要手段之一。实验室环境中的内孤立波与地形作用多为机理性研究, 对于内孤立波与海脊的作用, 研究集中于水下障碍物对内波的影响(Wessels, 1996; Sveen, 2002; Chen, 2011; Sutherland, 2015)。内孤立波与斜坡地形作用研究, 集中于破碎机制(Kao, 1985; Helfrich, 1986; Michallet, 1999; Boegman, 2005; Aghsaee, 2010; Sutherland, 2013; La Forgia, 2018; Nakayama, 2019)。

山脊地形对内孤立波的影响依赖于无因次化参数(障碍比)(Sveen, 2002), 定义为波谷距水面距离与障碍物最高点距水面距离的比值, 当<0.45时内波几乎不受障碍物的影响, 当介于0.45—0.55之间时障碍物会使内波发生形变但不会引起破碎, 此时浅化效应会使波后产生裂变, 当>0.55时内孤立波会发生破碎, 产生强烈的混合和能量耗散。内孤立波的透射、反射引起的能量变化依赖于振幅、深度参数和地形坡度(Sutherland, 2015), 且相互作用较强时会生成第二模态内孤立波(Vlasenko, 2001)。Boegman等(2005)通过内波实验发现, 波的破碎机制依赖于地形坡度与入射波波陡之比(Iribarren number, Ir)。他们借助于描述波浪破碎的方法, 将破碎机制分为内涌和翻转破碎。Sutherland等(2013)通过内孤立波与斜坡地形作用的实验, 重新定义了Ir数中的波陡, 并探讨了不同破碎类型与Ir数之间的关系, 将破碎类型分为内涌破碎、塌陷破碎、塌陷-翻转破碎、翻转破碎。Nakayama等(2019)认为, 以Ir数作为参数不能很好地区分内孤立波的塌陷和翻转破碎, 并定义了无量纲指标ISW=(/w)ISW2, 其中,和w分别为地形坡度和波陡,ISW为内孤立波的波动雷诺数, 当ISW大于7×106时为翻转破碎, 小于7×106为塌陷破碎。

海底山作为一种常见的海底地形, 是整个复杂海洋地貌的重要组成部分(Smith, 1988; Kitchingman, 2007)(图1)。平顶海山主要发育于西太平洋, 在南海西部陆坡, 基于多波束探测识别出13个平顶海山和1个平顶海丘(张伙带等, 2017)。斜压潮波与平顶海山相互作用, 会生成向海山中心辐射的内潮射线, 这种能量聚焦会增强海水混合, 并促进内波的局地产生(Vlasenko, 2018)。在内波与平顶海山相互作用导致破碎耗散方面, 前人研究较少, 需要进一步讨论。由于观测手段限制, 真实海洋中内孤立波的研究多基于剖面观测, 难以对内孤立波的传播、演化及耗散等过程的能量分配进行全面的分析。为进一步探究内孤立波与海底地形作用时波要素、能量、湍耗散率的时空变化, 本文进行了二维内孤立波实验, 分析内波与梯形地形的作用, 研究其经过平顶海山时的过程。通过粒子图像测速技术(Particle Image Velocimetry, PIV)研究内孤立波与地形作用时的流场结构, 聚焦于能量和湍耗散率的时空分布, 详细分析了不同破碎过程中湍流耗散的时间、空间变化特征, 定量地分析整个动力过程。

1 实验设置

本实验在中国海洋大学物理海洋实验室进行, 内波实验水槽的尺寸为6 m(长)×0.24 m(宽)×0.4 m (高), 主要实验装置的布设如图2所示。上下层水深1、2分别为4和28 cm, 上下层初始密度1、2分别为1.03和1.05 g/cm3。实验地形为三种高度的等腰梯形, 上底长r为40 cm, 底角为45°, 地形高度r分别为20、16、12 cm。实验采用重力塌陷法造波, 三种地形下造波的塌陷高度(d)均为4、6、8、10、12、14 cm, 总计18组实验。

图1 Sea Around Us Project分析所得潜在大海山分布（a）(Kitchingman et al, 2007)与平顶海丘地形剖面（b）

注: b为南海西部陆坡一平顶海丘地形剖面图，该海丘位于16°52.6′N, 111°12.8′E (张伙带等，2017)

图2 实验装置示意图

注: 图中1、2分别表示上下层水深,1、2分别表示上下层初始密度; 实验地形为三种高度的等腰梯形, 上底长r为40 cm, 底角为45°,r表示地形高度

实验利用PIV技术对地形所在区域的流场进行测量, 采用3个功率4 W、波长532 nm的激光器和2个分辨率为1920×1080像素的CCD(charge-coupled device)相机对测量区域成像, PIV示踪粒子的粒径为50 μm。为便于分析内孤立波与地形作用产生的湍流过程, CCD采用60帧进行图像采集。为实现内孤立波入射、反射、透射及其与地形作用产生能量耗散的全过程分析, 采用图像拼接技术以获取长1.5 m的流场数据(王金虎等, 2016; 黄鹏起等, 2016; 孟静等, 2018)。

2 计算方法

2.1 数据处理方法

采用PIV图像互相关算法PIVlab2.02对原始图像进行分析得到速度场, 并对数据中的奇异值进行过滤和插值处理, 最小查询窗口大小为8×8像素, 所得速度场的数据空间分辨率为3.9 mm。原始图像中, 在上下层水界面处堆积的粒子被激光打亮形成亮带, 通过对图像进行灰度分析得到界面的起伏, 提取振幅、波速等波要素。右传的内孤立波与地形前缘作用产生左传的反射波, 透射波经过地形继续向右传播。在地形前界面起伏的时间序列中读取入射波振幅, 以及随后的反射波振幅, 在地形后界面起伏的时间序列读取透射波振幅。

内波能量分为动能及有效势能, 实验将内孤立波与地形的作用考虑为二维过程, 只存在水平和垂向的速度。因此二维内波实验中, 单位体积的动能为

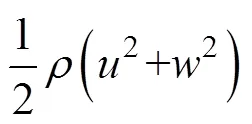
式中,和分别为水平和垂向速度,为当前流体质点密度。

本实验不能获取每一时刻的密度场, 利用灰度图像提取的界面进行有效势能计算, 采用Sutherland等(2015)的方法:

能量通量参考Michallet等(1999)的计算方法, 用每一时刻断面处垂向积分的能量乘以波速获得, 输入输出的总能量通过对能量通量时间积分获得:

其中,为波速,为总水深。0为断面水平位置,1、2为积分时间,f为能量通量, 选取合适的1和2可以得到输入输出的总能量t。

2.2 湍耗散率

本文使用直接法计算湍耗散率的空间分布, 对于牛顿流体耗散率定义为

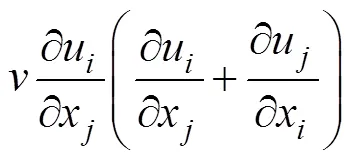
式中,u为脉动速度,x和x为坐标,、可取值1、2、3, 分别代表方向、方向、方向,为运动学黏度,S为二阶张量。基于连续方程和各向同性假设, 二维内孤立波的湍耗散率计算可简化为(Doron, 2001)

上划线表示取平均值, 式中的′、′均为脉动速度。考虑到内孤立波流场的特殊性, 在计算平均速度时没有进行简单的空间或时间平均, 而是依据灰度图像提取的界面将计算区域分为上层、界面、下层, 每个水平位置处的上、下层平均速度分别为该区域整层的垂向平均速度, 界面区域速度较慢, 平均速度取0, 厚度取2 cm。用瞬时速度减去平均速度, 即为所需脉动速度。

为了评估该计算方法的有效性, 本文将该方法计算的结果同能量输入输出差进行比较, 具体方法为: 选定一个可以包括地形的分析区域, 如图3所示, 图中虚线为计算区域的边界。在分析区域的边界处, 入射波能量输入, 反射和透射波能量输出, 在分析区域内, 内孤立波与地形作用发生能量耗散。理想情况下, 输入总能量与输出总能量之差等于分析区域内耗散总能量与内孤立波经过后区域内的能量之和。耗散的总能量通过对湍耗散率进行空间时间积分获得, 其中空间范围为分析区域, 时间范围从波进入区域前到波完全离开区域后。

图3 能量耗散计算方法

3 实验结果

本实验中, 不同重力塌陷高度, 所产生的入射波振幅在2—6 cm之间, 障碍比(Sveen, 2002)在0.3—0.82之间(表1),=(A+1)/(1+2–r),A为入射波振幅,1、2分别为上下层水深,r为地形高度。地形升高对内孤立波影响越来越显著, 在大振幅(5—6 cm)与大地形(20 cm)作用时会发生塌陷-翻转破碎(>0.7); 而中等振幅(4—5 cm)与大地形或大振幅与中等地形(16 cm)作用时, 会因内孤立波后缘变陡发生翻转, 产生翻转破碎(0.57≤≤0.7); 小地形(12 cm)对内孤立波的影响很小, 仅会使大振幅内波产生裂变(0.45≤<0.57)。

表1 基本参数

Tab.1 The main parameters for calculation

3.1 基本要素分布

对实验所得速度场进行计算, 得到涡度和湍耗散率的空间分布。图4通过涡度和湍耗散率, 揭示内孤立波与梯形地形作用的典型过程。所有实验内孤立波均从左侧入射向右传播。图4a1中, 右传的入射波上层水平流速向右, 下层水平流速向左, 上下层界面处流速较小, 水平速度垂向剪切在界面处产生较强的涡度和能量耗散(图4a1、4b1)。图4a1中, 内孤立波引起波前下降波后上升的垂向流动。该实验条件下, 波会在地形前缘破碎, 引起强烈的能量耗散和水体混合, 图4a和图4b定性展示了该过程。图4a2中, 浅化过程使爬坡处的界面迅速下凹, 波的后缘变陡, 同时波前缘已经传到地形上方平顶处。图4a3中, 内孤立波与地形碰撞发生破碎, 在地形前缘生成强涡旋,图4b3同时产生强能量耗散, 已经传到地形上方的波继续向右传播。图4a4和图4b4中, 涡度和湍耗散率在地形前缘扩散, 在图4b4地形左顶角右侧可以观察到因波后缘翻转破碎生成的湍涡, 同时地形左侧左传的反射波使界面处出现正涡度和湍流耗散(图4a4黑色虚线, 图4b4白色虚线)。图4a5和图4b5, 涡度和湍耗散率继续扩散, 强度减弱, 已由之前的大尺度涡旋和湍涡, 分散为小涡和和小尺度湍流运动, 同时右传的透射波正离开地形。

涡度和湍耗散率强度空间分布基本一致, 表明湍流与涡旋有着密切的相关性。内孤立波与地形作用时, 既与地形碰撞发生破碎, 又在波后缘发生翻转破碎, 因此该实验条件下的破碎机制类似于塌陷-翻转破碎(Sutherland, 2013; Nakayama, 2019)。图4a5中地形后缘有一沿地形的上升流, 表明内孤立波不仅会在地形前缘产生强烈作用, 也会在离开地形时受到地形后缘影响。

图5中地形高度为16 cm, 内波界面没有在爬坡时迅速下凹, 而是因浅化效应使波后缘变陡(图5a2), 在地形上方平顶处等密度面翻转发生破碎(图5b4), 该条件下的破碎机制为翻转破碎(Sutherland, 2013; Nakayama, 2019)。值得注意的是, 虽然内孤立波在后缘发生翻转破碎, 没有直接与地形作用, 但内波经过地形前缘后, 增强的下层流在地形左顶角处生成一个强涡(图5a3), 该涡被波后上升流逐渐抬升(图5a4), 在抬升过程中引起能量耗散(图5b4、图5b5), 最终消亡(图5a5); 另外, 相比于图4(地形高度20 cm), 该组实验的能量耗散较弱, 变强的透射波在地形后缘产生更强的上升流。两个典型的内孤立波与地形作用过程中, 强作用区域均在地形前缘。

图6为内孤立波在地形前缘不同断面的时间序列, 图6a为界面起伏、6b为能量垂向积分、6c为湍耗散率垂向积分, 图6b、6c中虚线表示最大能量密度。图6a中, 内孤立波的振幅在爬坡过程中达到最大, 最大值超过入射波振幅的2倍。能量密度同样在爬坡过程中达到极值, 在地形上方能量密度减小(图6b)。图6c中虚线和图6b中为同一条, 因此图6c中虚线处的起伏是界面处剪切引起的湍流耗散, 随后的起伏是地形前缘内波破碎引起的局地湍流耗散。图6表明, 该组实验条件下局地耗散远大于剪切耗散; 局地耗散的峰值晚于剪切耗散出现; 局地耗散在地形左顶角附近最强。

图4 塌陷-翻转破碎过程中的涡度(a)和湍耗散率(b)

注:表示水平方向距离,表示垂直方向距离; 地形高度为20 cm, 入射振幅为5.0 cm, 图像时间间隔为2 s; 灰色填充表示地形所在区域; a4、a5中黑色虚线框内为反射波在界面处引起的正涡度, b4中白色虚线框内为反射波在界面处引起的湍耗散

图7中入射振幅小于图6, 相互作用过程较弱, 振幅和能量仍会在爬坡处增大。值的注意的是, 在该实验条件下, 图7c中0.18和0.20 m处的断面峰值在虚线附近, 表明该峰值对应浅化过程中随波增强的剪切耗散。随后在0.16和0.14 m处的峰值, 为波与地形作用引起的局地耗散, 这两种耗散的强度在同一量级。

图6—图7表明, 内孤立波振幅在爬坡过中有明显的增大, 所有实验条件下振幅增长如图8所示。图中横坐标为无量纲入射振幅(入射波振幅与上层水深的比值), 纵坐标为爬坡振幅最大值与入射振幅之比。不同地形下, 比值均随入射振幅呈线性增长, 小地形下增长率较低, 最大时仅为入射波振幅的1.2倍, 大地形下振幅极值已经超过入射波振幅的2倍。内孤立波未发生翻转破碎实验中, 振幅在达到极值后逐渐减小恢复到稳定值, 这个过程给波尾的裂变提供能量; 内孤立波破碎实验中, 振幅逐渐增大发生破碎, 振幅在破碎前一时刻达到最大, 振幅增长率越大能量耗散越多。

3.2 能量分配

计算内波传播过程中的能量分配如图9所示, 通过式(3)、(4)计算三种地形高度下输入、输出的总能量。20 I、16 I、12 I分别表示地形高度20、16、12 cm的输入总能量,20 O、16 O、12 O表示输出总能量。输入总能量为入射波能量, 与无量纲入射波振幅满足二次函数关系。地形增高和入射波振幅增大都会加强地形对内孤立波的影响, 使波经过地形时能量耗散增强, 导致输出的总能量减小。

图5 翻转破碎过程中的涡度(a)和湍耗散率(b)

注:表示水平方向距离,表示垂直方向距离; 地形高度为16 cm, 入射振幅为5.1 cm, 图像时间间隔为2 s

图6 大振幅内孤立波与地形相互作用的界面(a)、能量(b)和湍耗散率(c)

注:表示牛顿流体耗散率; 地形高度为20 cm, 入射振幅为5.8 cm; b、c中的虚线均表示最大能量密度所在时刻

图7 小振幅内孤立波与地形相互作用的界面(a)、能量(b)和湍耗散率(c)

注: 地形高度为20 cm, 入射振幅为3.5 cm; b、c中的虚线均表示最大能量密度所在时刻

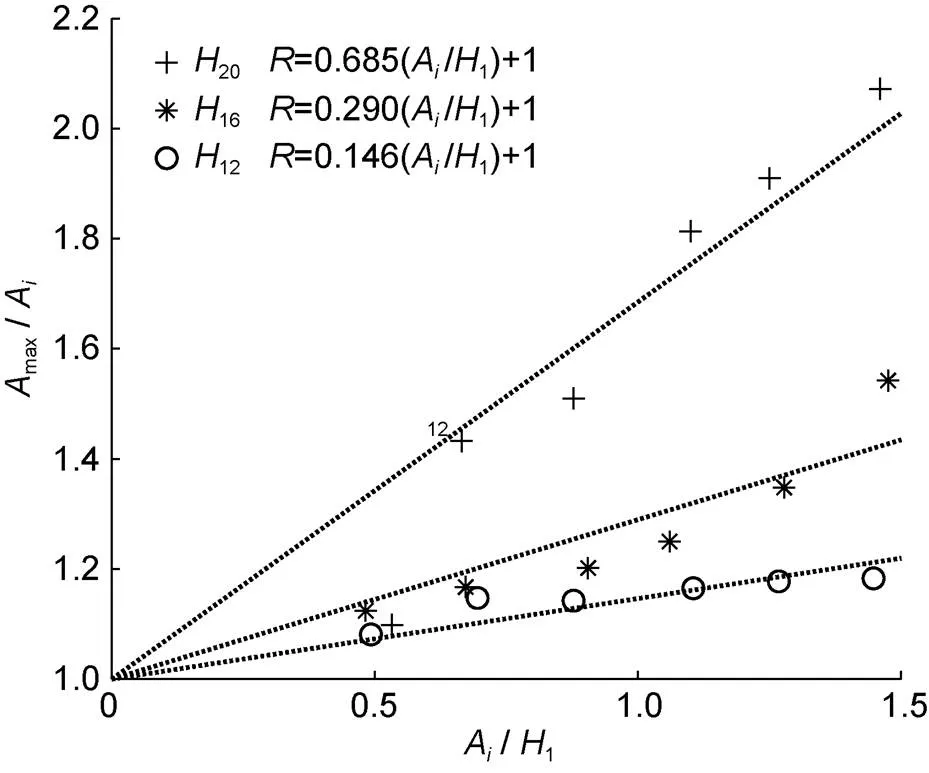
图8 振幅增长率(Amax/Ai)随无量纲振幅(Ai/H1)的变化

注:max为振幅极值,A为入射波振幅; 三条虚线为不同地形高度下, 无量纲振幅与振幅增长率的线性拟合,20、16、12分别表示地形高度20、16、12 cm,为振幅增长率(max/A)。

图10a1、10a2中, 能量差和直接法计算的耗散在振幅较小时差异较小, 但随入射振幅增大, 直接法计算的能量耗散开始逐渐小于能量差计算的耗散, 且地形越高差异越大。图10b为直接法积分和能量差法计算的能量耗散比值, 两种方法的计算差异, 随入射振幅增大, 在无量纲入射振幅增涨到一定值时(1—1.5), 比值减小速率明显变缓, 维持在0.4左右。

图9 输入输出总能量与无量纲振幅(Ai/H1)的关系

注:20 I、16 I、12 I: 输入总能量,20 O、16 O、12 O: 输出总能量; 虚线为所有地形高度输入总能量的二次拟合

图10 能量损失(a1)与湍耗散率积分(a2)以及湍耗散率积分与能量损失比值(b)

注:20、16、12分别表示地形高度20、16、12 cm,d为塌陷高度;为直接法积分与能量损失的比值, 图b中虚线为负一次方拟合

两种计算方法所求能量耗散在同一量级, 考虑到能量差法计算的能量耗散相对准确, 认为湍耗散率积分计算的能量耗散在大振幅时偏小。这可能是部分湍流尺度小于速度网格的分辨率, 以及过滤测量时产生的奇异值共同导致的。

将所有断面能量垂向积分, 做成时间序列, 得到能量时空分配(图11)。图11a中, 地形左侧20—30 s为入射波引起的能量变化, 35—45 s为反射波, 地形右侧35—45 s为透射波引起的能量变化, 36 s后地形前缘出现左传的能量扩散。图11a中黄色虚线可能对应第二模态内孤立波(也可能为向右传播的重力流), 其波速远小于第一模态, 为2.6 cm/s(该组实验下第一模态波速为10.4 cm/s)。图11b中, 能量在爬坡时增大, 持续约2 s, 在湍流耗散最强时刻前后, 能量迅速衰减。

3.3 湍流耗散

3.1节的定性描述中, 大振幅内孤立波与地形作用会引起强烈的湍流耗散, 这一节将定量讨论该过程。图4、图5中, 湍耗散最强的区域分布在地形前缘, 因此在该区域寻找局地湍耗散率的极值, 在波抵达地形前寻找界面处剪切引起湍耗散率的极值。局地的耗散率为5×5点区域平均, 剪切湍耗散率为3×15点区域平均。两种耗散的计算范围不同, 结果分开讨论。

图12为每组实验湍耗散率极值和无因次振幅的对应关系, 图12a中的剪切耗散与无因次振幅呈线性关系, 量级为10-5m2/s3。地形高度16 cm时波速相对于其他两组较快, 剪切耗散偏大。内孤立破碎条件下(表1), 局地耗散极值随无因次振幅呈指数增长, 最大值量级已接近10-3m2/s3; 不破碎条件下(表1), 局地耗散极值呈线性增长。但在地形20 cm的最大振幅实验中局地耗散极值不再增长(图12b三角形), 这表明该实验条件已使局地耗散极值达到最大, 需要更大振幅的实验进一步讨论此问题。

图13为地形高度16和20 cm, 每一时刻局地耗散极值的时间序列, 在内波与地形作用较强时, 局地耗散极值会强于10-4m2/s3持续数10 s。图中大部分曲线是单峰结构, 个别曲线呈双峰结构。在地形高度20 cm塌陷高度10 cm时, 极值曲线出现双峰结构, 峰值时刻的湍耗散率空间分布如图14所示, 黄色方框为湍耗散率极值点所在位置。两个峰分别对应浅化过程中的剪切加强和波后缘的翻转破碎。振幅较小时, 不产生破碎混合, 极值仅为增强的剪切耗散, 所以曲线呈单峰结构; 较大振幅与高地形作用时, 混合过于强烈且破碎引起的耗散很强, 导致很多过程交织在一起, 仅能突出最强的破碎混合过程, 所以曲线也为单峰结构。

为把握耗散的整体过程, 地形左顶角附近40 cm区域内, 湍耗散率空间平均的时间序列如图15所示。振幅越大耗散持续的时间越长, 极值也越大, 量级区间为10-6—10-4m2/s3, 极值增长远没有局地耗散迅速。图中星号为每组实验局地耗散最大值发生时刻。在地形20和16 cm时, 局地耗散极值和空间平均极值对应时刻吻合较好, 这表明当局地耗散最强时, 整个空间内的耗散也最强。但在地形12 cm时局地耗散极值对应时刻有滞后现象, 这表明地形增强的剪切耗散极值, 在一部分波离开计算区域时出现。将湍耗散率空间平均后会减弱一些小尺度过程, 很难再观察到双峰结构, 但图13中双峰结构对应的曲线, 在图15中相对于其他曲线更为扁平。

图11 能量时空分布(a)和图a红框区域 (b)

注: 地形高度为20 cm, 入射振幅为5.0 cm; 红色虚线为每一时刻单位水平区域能量极值位置; 36 s和31 s处的蓝色虚线分别对应湍流耗散最强的时刻和浅化过程中振幅出现极值的时刻, 黄色虚线处为第二模态内孤立波或重力流引起的能量变化

图12 湍耗散率极值与无因次振幅

注: a: 剪切湍耗散率; b: 局地湍耗散率; 图a虚线为线性拟合; 图b虚线为内波破碎条件下用指数拟合, 不破碎用线性拟合, 三角形所标出的点不参与拟合

4 结论与展望

文章通过实验分析内孤立波经过平顶海山时波要素、能量、湍耗散率的变化, 得到以下结论:

(1) 内孤立波经过平顶海山时, 会发生裂变破碎等强混合过程。这与陆坡地形处内孤立波破碎混合过程相似(Sutherland, 2013; Nakayama, 2019), 但在平顶海山区域, 内孤立波会发生透射, 其混合及波形演变与地形障碍比密切相关。本实验的障碍比在0.30—0.82,>0.7时会发生塌陷-翻转破碎; 0.57≤≤0.7时会发生翻转破碎; 0.45≤<0.57时波尾会出现裂变。波与地形前缘作用, 振幅增大、能量密度增强、能量耗散最为强烈; 与地形后缘作用, 会引起强上升流。

图13 局地耗散率极值时间序列

注: a: 地形高度16 cm, b: 地形高度20 cm; 图例中数字为塌陷高度(cm)

图14 局地耗散率峰值时刻的湍耗散率空间分布

注: 地形高度20 cm, 入射振幅4.4 cm; 黄色方框为湍耗散率极值点所在位置

(2) 入射波的能量与塌陷高度呈二次函数关系, 透射波与反射波的能量和随地形升高减小。

(3) 通过能量通量计算的能量损失与湍耗散率积分计算的能量耗散在同一量级。在入射波振幅较大时, 后者为前者的40%左右。这是部分湍流尺度小于速度网格的分辨率, 以及过滤测量时产生的奇异值等因素导致的。

(4) 波与地形作用前, 剪切耗散量级为10-5m2/s3, 与实测海洋内孤立波传播时界面处的耗散率极值相当。波与地形作用时, 区域平均湍耗散率在10-6—10-4m2/s3之间; 内波破碎引起的局地湍耗散率极值与入射波振幅呈指数关系, 所有实验中局地耗散的最大值接近10-3m2/s3。

图15 湍耗散率空间平均时间序列

注: *为每组实验局地耗散最大值发生时刻

(5) 局地耗散极值时间序列在部分过程中呈双峰结构, 双峰结构中不同的峰分别对应剪切加强、翻转破碎。较强的破碎混合过程会将这两种情况交织在一起, 使曲线呈单峰结构, 较弱的相互作用过程仅有剪切耗散, 曲线也呈单峰结构。

本文通过计算发现, 获得湍耗散率的观测手段和计算方法都需要改进。实验采用地形为理想地形且仅研究二维情况, 不足以研究内孤立波与海山作用的全部过程, 后续实验应模拟实际海底地形以及开展三维实验。

王金虎, 陈 旭, 徐 洋, 2016. 粗糙地形对内波生成影响的实验研究. 海洋与湖沼, 47(4): 706—713

张伙带, 朱本铎, 黄文星等, 2017. 南海西部陆坡平顶海山和海丘地形特征. 海洋地质前沿, 33(8): 11—17

孟 静, 王树亚, 陈 旭等, 2018. 内孤立波对小直径直立桩柱作用力的实验研究. 海洋与湖沼, 49(3): 535—540

黄鹏起, 陈 旭, 孟 静等, 2016. 内孤立波破碎所致混合的实验研究. 海洋与湖沼, 47(3): 533—539

Aghsaee P, Boegman L, Lamb K G, 2010. Breaking of shoaling internal solitary waves. Journal of Fluid Mechanics, 659: 289—317

Bai X L, Li X F, Lamb K G, 2017. Internal solitary wave reflection near Dongsha Atoll, the South China Sea. Journal of Geophysical Research: Oceans, 122(10): 7978—7991

Boegman L, Ivey G N, Imberger J, 2005. The degeneration of internal waves in lakes with sloping topography. Limnology and Oceanography, 50(5): 1620—1637

Cai S Q, Xie J H, He J L, 2012. An overview of internal solitary waves in the South China Sea. Surveys in Geophysics, 33(5): 927—943

Chen C Y, 2011. Statistical and dynamical analyses of propagation mechanisms of solitary internal waves in a two-layer stratification. Journal of Marine Science and Technology, 16(1): 100—114

Colosi J A, Kumar N, Suanda S H, 2018. Statistics of internal tide bores and internal solitary waves observed on the inner continental shelf off Point Sal, California. Journal of Physical Oceanography, 48(1): 123—143

Davis K, Arthur R, Reid E, 2017. Fate of internal waves on a shallow shelf. In: Proceedings of the 70th Annual Meeting of the APS Division of Fluid Dynamics. Denver, Colorado: American Physical Society

Doron P, Bertuccioli L, Katz J, 2001. Turbulence characteristics and dissipation estimates in the coastal ocean bottom boundary layer from PIV Data. Journal of Physical Oceanography, 31(8): 2108—2134

Droghei R, Falcini F, Casalbore D, 2016. The role of Internal Solitary Waves on deep-water sedimentary processes: the case of up-slope migrating sediment waves off the Messina Strait. Scientific Reports, 6(1): 36376

Garrett C, Munk W, 1979. Internal waves in the ocean. Annual Review of Fluid Mechanics, 11: 339—369

Gerkema T, Zimmerman J T F, 2008. An Introduction to Internal Waves. Lecture Notes. Royal NIOZ (Royal Netherlands Institute for Sea Research), Texel, Netherlands. 1—207

Grimshaw R, Pelinovsky E, Talipova T, 2010. Internal solitary waves: propagation, deformation and disintegration. Nonlinear Processes in Geophysics, 17(6): 633—649

Grimshaw R H J, Ostrovsky L A, Shrira V I, 1998. Long nonlinear surface and internal gravity waves in a Rotating Ocean. Surveys in Geophysics, 19(4): 289—338

Helfrich K R, Melville W K, 1986. On long nonlinear internal waves over slope-shelf topography. Journal of Fluid Mechanics, 167: 285—308

Jackson C, 2007. Internal wave detection using the Moderate Resolution Imaging Spectroradiometer (MODIS). Journal of Geophysical Research: Oceans, 112(C11): C11012

Jia T, Liang J J, Li X M, 2018. SAR observation and numerical simulation of internal solitary wave refraction and reconnection behind the Dongsha Atoll. Journal of Geophysical Research: Oceans, 123(1): 74—89

Kao T W, Pan F S, Renouard D, 1985. Internal solitons on the pycnocline: generation, propagation, and shoaling and breaking over a slope. Journal of Fluid Mechanics, 159: 19—53

Kitchingman A, Lai S, Morato T, 2007. How many seamounts are there and where are they located? In: Pitcher T J, Morato T, Hart P Beds. Seamounts: Ecology, Fisheries & Conservation. Oxford, UK: Blackwell Publishing, 26—40

Klymak J M, Legg S, Alford M H, 2012. The direct breaking of internal waves at steep topography. Oceanography, 25(2): 150—159

Klymak J M, Pinkel R, Rainville L, 2008. Direct breaking of the internal tide near topography: Kaena Ridge, Hawaii. Journal of Physical Oceanography, 38(2): 380—399

La Forgia G, Adduce C, Falcini F, 2018. Laboratory investigation on internal solitary waves interacting with a uniform slope. Advances in Water Resources, 120: 4—18

Michallet H, Ivey G N, 1999. Experiments on mixing due to internal solitary waves breaking on uniform slopes. Journal of Geophysical Research: Oceans, 104(C6): 13467—13477

Moum J N, Farmer D M, Smyth W D, 2003. Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. Journal of Physical Oceanography, 33(10): 2093—2112

Moum J N, Gregg M C, Lien R C, 1995. Comparison of turbulence kinetic energy dissipation rate estimates from two ocean microstructure profilers. Journal of Atmospheric and Oceanic Technology, 12(2): 346—366

Moum J N, Klymak J M, Nash J D, 2007. Energy transport by nonlinear internal waves. Journal of Physical Oceanography, 37(7): 1968—1988

Nakayama K, Sato T, Shimizu K, 2019. Classification of internal solitary wave breaking over a slope. Physical Review Fluids, 4(1): 014801

Orr M H, Mignerey P C, 2003. Nonlinear internal waves in the South China Sea: observation of the conversion of depression internal waves to elevation internal waves. Journal of Geophysical Research: Oceans, 108(C3): 3064

Osborne A R, Burch T L, 1980. Internal solitons in the Andaman Sea. Science, 208(4443): 451—460

Raju N J, Dash M K, Dey S P, 2019. Potential generation sites of internal solitary waves and their propagation characteristics in the Andaman Sea-a study based on MODIS true-colour and SAR observations. Environmental Monitoring and Assessment, 191(S3): 809

Reeder D B, Ma B B, Yang Y J, 2011. Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Marine Geology, 279(1—4): 12—18

Shimizu K, Nakayama K, 2017. Effects of topography and Earth’s rotation on the oblique interaction of internal solitary-like waves in the Andaman Sea. Journal of Geophysical Research: Oceans, 122(9): 7449—7465

Smith D K, 1988. Shape analysis of Pacific seamounts. Earth and Planetary Science Letters, 90(4): 457—466

Sutherland B R, Barrett K J, Ivey G N, 2013. Shoaling internal solitary waves. Journal of Geophysical Research: Oceans, 118(9): 4111—4124

Sutherland B R, Keating S, Shrivastava I, 2015. Transmission and reflection of internal solitary waves incident upon a triangular barrier. Journal of Fluid Mechanics, 775: 304—327

Sveen J K, Guo Y K, Davies P A, 2002. On the breaking of internal solitary waves at a ridge. Journal of Fluid Mechanics, 469: 161—188

Trevorrow M V, 1998. Observations of internal solitary waves near the Oregon coast with an inverted echo sounder. Journal of Geophysical Research: Oceans, 103(C4): 7671—7680

Vlasenko V I, Hutter K, 2001. Generation of second mode solitary waves by the interaction of a first mode soliton with a sill. Nonlinear Processes in Geophysics, 8(4—5): 223—239

Vlasenko V, Hutter K, 2002. Numerical experiments on the breaking of solitary internal waves over a slope–shelf topography. Journal of Physical Oceanography, 32(6): 1779—1793

Vlasenko V, Stashchuk N, 2007. Three-dimensional shoaling of large-amplitude internal waves. Journal of Geophysical Research: Oceans, 112(C11):C11018

Vlasenko V, Stashchuk N, Nimmo-Smith W A M, 2018. Three-dimensional dynamics of baroclinic tides over a seamount. Journal of Geophysical Research: Oceans, 123(5): 1263—1285

Wessels F, Hutter K, 1996. Interaction of internal waves with a topographic sill in a two-layered fluid. Journal of Physical Oceanography, 26(1): 5—20

Xu J X, Xu J S, Chen Z W, 2012. Enhanced mixing induced by internal solitary waves in the South China Sea. Continental Shelf Research, 49: 34—43

Yang Y J, Fang Y C, Chang M H, 2009. Observations of second baroclinic mode internal solitary waves on the continental slope of the northern South China Sea. Journal of Geophysical Research: Oceans, 114(C10):C10003

Zhao Z X, Alford M H, 2006. Source and propagation of internal solitary waves in the northeastern South China Sea. Journal of Geophysical Research: Oceans, 111(C11):C11012

LABORATORY STUDY ON ENERGY DISSIPATION OF INTERNAL SOLITARY WAVES IN GUYOTS

GUO Yu-Lin1, MENG Jing4, XU Yu5, JIA Cun2, LIU Juan3, CHEN Xu1, YU Yu-Jun1

(1. Key Laboratory of Physical Oceanography, Ocean University of China, Qingdao 266003, China; 2. Third institute of oceanography, MNR, Ocean Dynamic Lab, Xiamen 361005, China; 3. Beijing Institute of Applied Meteorology, Beijing 100029, China; 4. College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China; 5. College of Engineering Oceam University of China, Qingdao 266100, China)

Energy dissipation and mixing induced by internal wave breaking are important dynamic physical processes in the ocean. Upon 2-dimensional laboratory experiments in an internal wave tank, the evolution of an interfacial internal solitary wave (ISW) passing by an underwater trapezoidal topography mimicking a guyot was examined. The temporal and spatial variation of wave parameters, energy and turbulent dissipation rate during ISW interaction with guyots were analyzed. The first mode (Mode-1) ISW was generated in the two-layered stratified fluid system through standard lock-release method. The flow field structure of the internal solitary waves and the topography were obtained by particle image velocimetry (PIV), and the whole process was quantitatively analyzed. The velocity field of the Mode-1 ISW propagation was visualized by PIV. Results show that if the topography was moderately large, the wave was observed to shoal and break. The amplitude and energy could increase rapidly when the ISW climbed to the slope, during which intense energy dissipation appeared in the front edge of the topography. The energy of incident wave was in quadratic function to the collapse height, and the energy of transmitted wave and reflected wave decreased with the rise of topography. The time series of the local dissipation extremum shows bimodal peaks in several experiments, which corresponds to the shear dissipation boosting and plunging breaker. The average dissipation rate in the front edge of the topography was 10–5m2/s3in magnitude and the maximum of local turbulence dissipation rate was close to the magnitude of 10–3m2/s3. The extreme value of local turbulent dissipation rate was exponential to the incident wave amplitude.

internal solitary wave breaking; energy dissipation; turbulent dissipation; particle image velocimetry (PIV)

* 国家海洋局海洋遥测工程技术研究中心开放基金, 2017005号; 海洋环境保障创新开放基金, HHB003号; 中央高校基本科研业务费专项, 202051015号。郭钰林, 硕士研究生, E-mail: 754454291@qq.com

徐 昱, 实验师, E-mail: xuyu@ouc.edu.cn

2021-01-06,

2021-03-06

P731.24

10.11693/hyhz20210100004