工程流体力学教学模式探讨*
2021-07-21于萍郭华锋刘磊李龙海
◆于萍 郭华锋 刘磊 李龙海
0 前言
传统教学的“三中心模式”,即教材为中心、教师为中心、教室为中心,使得教学资源封闭、滞后,教学手段单一,知识传授仅限于课堂之上,不利于教师和学生综合素质提升[1]。工程流体力学是工科类专业的学科基础课,和实际工程应用联系紧密,主要研究流体静力学、流体动力学、流体管流和绕流等问题。这门课程知识点繁多,抽象难懂,逻辑性强,传统教学模式下,学生在学习时只是被动地接受而非主观地吸收,课堂参与度低,再加之对流体运动的感性认识贫乏,导致学习效果不佳[2-3]。
本文提出将FLUENT软件模拟工程案例引入教学中,让学生对生产生活中遇到的实际案例进行建模、计算、分析,从而加深对抽象概念、公式的理解,培养学习兴趣,提高教学质量[4-5]。这种新模式改变了传统的三中心教学模式,教学时空不限于课堂之上,提倡教与学双向互动,即以学生为主体、教师为主导,学生主动、开放地学习,培养问题解决能力、反思能力和问题迁移能力。
1 传统教学与FLUENT案例教学对比
教学资源 传统的教学资源是封闭式的,局限在课本内容之内。这会造成学生完全信奉课本上的知识,认为课本知识是全面的、正确的,导致眼界不宽阔,不会学以致用,缺少创新性和创造性,生搬硬套,亦步亦趋。教材《工程流体力学》内容抽象难懂,有大量的定理和公式,仅靠课本上的基本内容,学生理解起来比较困难,进而产生厌学情绪,缺乏学习动力[4,6-7]。在课堂中引入FLUENT模拟相关工程案例,使学生将课本知识和实际生产生活问题相互关联,他们会对陌生、抽象的知识产生比较直观、具体的认识,理解起来更加容易,体会到学以致用的乐趣。
教学方法 传统的教学方法以教师为中心,采用填鸭式教学,学生被动地接受知识,容易产生依赖心理,全靠死记硬背,不利于培养独立思考的能力。教师往往依照课本内容顺序进行授课,这种方式忽略了知识点之间的相互联系,没有突出内容主线,知识碎片化,导致学生难以形成课程内容的整体框架,不利于知识点的理解和掌握。假如在教学过程中让学生利用FLUENT软件模拟相关的工程案例,并对模拟结果进行分析,这个过程不仅能提高学生的课堂参与程度,更重要的是可以促使学生主动学习、深层学习和深层理解,将课堂上碎片化的知识联系起来,培养独立思考、解决问题的能力,实现“以教师为中心”向“以学生为中心”转变[5,8]。
时空结构 传统的教学时间、地点仅限在课堂之上,忽略了学生的个体差异,不利于学生创新性和自主学习能力的培养。工程流体力学课程知识点繁多、抽象难懂,仅靠课堂时间学习难以掌握,需要更多的学习时间。将FLUENT软件模拟工程案例引入教学中,让学生课后收集材料,查阅相关文献,使获取知识的时间和空间得到扩展,学生个体和教师之间的交互增多,有利于教师了解每一个学生的学习情况。大学的课堂应该以学生主动学习为主,教师加以引导,不仅是知识的传递,更应该是学习方法、学习习惯、思维能力的培养[9-10]。
2 FLUENT案例教学举例
案例描述 黏性流体绕流圆柱是流体力学经典问题之一。如图1所示,直径d=40 mm的圆柱体放置在长L=1 000 mm,高H=200 mm的流体区域,流体以速度v从左往右流动[11]。在实际生产生活中,这是比较常见的现象,如风吹过烟囱、旗杆,水流过桥墩,等等。

图1 黏性流体绕流圆柱
案例实施 学生根据实际案例在Gambit软件中建立数学模型,并对数学模型进行网格划分,图2为数学模型中靠近圆柱的部分网格。数学模型的入口采用速度入口边界条件,出口为自由出流边界条件,其余设为固体壁面边界条件。

图2 数学模型
将建立好的数学模型在FLUENT软件中进行计算。黏性流体绕流圆柱的过程将会涉及连续性方程、伯努利方程、动量方程、曲面边界层分离等知识[12],如图3所示。
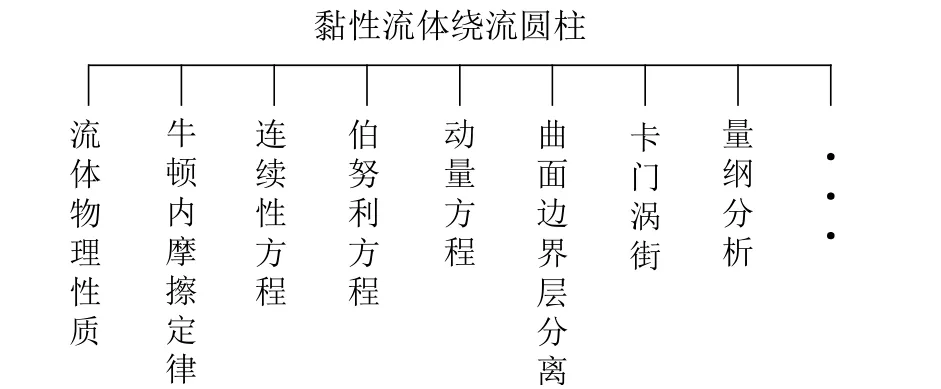
图3 知识点结构图
数学模型计算过程中改变入口流体的速度,入口流体的雷诺数Re随之改变,流体绕流圆柱的流场分布情况也不同。流体雷诺数的计算公式:

式中:ρ为来流流体的密度,单位为kg/m3;v为来流流体的速度,单位为m/s;d为圆柱体的直径,单位为m;μ为来流流体的动力黏度,单位为Pa·s。
案例数值模拟结果分析 在数值模拟过程中涉及的内容几乎囊括工程流体力学课本上的所有知识点。实验研究表明[12]:当Re<1时,黏性流体绕流圆柱,流线基本对称,没有明显的边界层分离现象。图4-a是雷诺数Re=0.5时的数值模拟结果,和实验描述的结果吻合。在模拟过程中,学生需要掌握流体力学的三个基本方程,即连续性方程、动量方程、伯努利方程;以及流体力学中的基本概念和性质,如理想流体和黏性流体、定常流和非定常流、流线和迹线、流体质点和空间点等概念的区分。此时模拟的流场中每一空间点的运动参数都不随时间变化,仅是位置的函数,所以是黏性流体的定常流动。此外还涉及牛顿内摩擦定律、边界层等概念。在模拟过程中,学生将晦涩难懂的抽象概念和实际工程案例建立联系,更容易理解,学习效果更好。
实验研究表明[12]:当4<Re<40时,在圆柱体后面出现明显的边界层分离现象,出现一对不稳定的旋转方向相反的对称旋涡。图4-b是雷诺数Re=20时的数值模拟结果,和实验结果吻合得很好。模拟过程涉及边界层的概念以及曲面边界层分离过程等知识点。如果仅靠文字描述,比较抽象,难以理解;如果学生通过FLUENT软件将这个过程模拟出来,并对照文字描述进行分析,那涉及的抽象概念就会变成直接的感官刺激,会有更深层次的理解和印象,既复习了所学知识,又将碎片化的知识点联系起来,形成自己的知识框架。
当圆柱后面的旋涡增大到一定程度,就会被主流流体带走。当60<Re<5 000时,在圆柱体后面出现两列不对称、交替脱落的旋转方向相反的旋涡,并随着来流流体主流方向向下游运动,形成卡门涡街[12]。图4-c是雷诺数Re=200时的数值模拟结果,和实验结果吻合,这时流场中每一空间点的运动参数的自变量除了位置坐标,还包括时间,所以是非定常流动。

图4 黏性流体绕流圆柱速度场
学生通过对该案例的建模、计算、分析,更深层次地了解了流体力学的基本概念,以及连续性方程、伯努利方程、动量方程、曲面边界层分离等知识,并通过数值模拟软件把书本上枯燥的文字表述变为生动的图片、视频。
3 结束语
本文提出将FLUENT数值模拟软件引入工程流体力学教学中,并数值模拟、分析经典案例——黏性流体绕流圆柱,通过和实验结果的对比,证明该教学模式的正确性、可行性。在模拟过程中,学生主动翻阅资料,查找相关知识,学习由被动变为主动,有助于掌握数值模拟软件,培养解决问题能力、独立思考能力和问题迁移能力,为以后工作和科研打下良好基础。
