轴承共腔结构涡轴发动机相似模型设计

刘 准 ，廖明夫 ，邓旺群 ，刘文魁

（1.西北工业大学动力与能源学院，西安710129；2.中国航发湖南动力机械研究所，湖南株洲412002）

0 引言

国内外新一代的涡轴发动机采用了燃气发生器转子和动力涡轮转子共用的轴承共腔结构取代了原有涡轴发动机独立的排气框架和燃气发生器转子后支点结构，具有体积小、工作转速高以及双转子系统耦合振动明显等特点，试验驱动系统动力学特性相对复杂同时传感器的布置变得较为困难。因此，采用临界转速较低、体积较大的试验模型转子进行转子动力学试验是一种廉价、高效的选择。

针对双转子系统的动力学特性分析在国内外已经得到了相对完善的研究。邓旺群等[1]针对涡轴发动机高速转子进行了动力学特性的计算；Chiang 等[2]分析了单转子和双转子的耦合动力学特性；章健等[3]研究了共用支承结构即共腔结构的传力特性和耦合特性，为轴承共腔结构双转子系统的动力学计算提供了参照。

此外，很多研究已经对单转子系统的相似设计进行了详尽地分析。其中，罗忠等[4-5]分析了转子动力学相似中轴承参数以及薄壁件结构的影响；王永亮等[6]在考虑陀螺效应的情况下讨论了单转子系统的转子动力学相似准则；Wu[7]详细对比了通过相似模型与原型转子的振型对应关系，在实际计算中单转子相似模型与原型转子的振型相似度约为70%。

在本研究中作为设计目标的动力学相似试验器采用空心电机驱动燃气发生器，因此动力涡轮与燃气发生器转子的长度差更大，动力涡轮转子和燃气发生器转子无法保持相同的相似比。因此，结合双转子系统的动力学耦合计算方法对现有的转子动力学相似理论进行了小的改进，使拥有不同相似比的转子正确耦合，保证相似后的轴承共腔结构模拟双转子系统总体上与原发动机转子在振型和临界转速上比例相似。此外，由于试验模型在相似尺寸缩放过程中的小结构与涡轴发动机上的零件不可能完全成比例，因此试验模型中存在许多畸变。为了减小这些畸变的不利影响，在给定的临界转速相似比和双转子长度相似比条件下，本文提出了一种基于有限元方法和多岛遗传算法的方法，并通过计算实例验证了该方法和理论的有效性。

1 模态分析与相似理论准备

1.1 模态分析

有限元分析方法是一种离散连续系统的方法，通过建立运动微分方程的离散微分模型，并进行数值求解，计算和分析系统的动态特性。在本文工作中，采用1 维有限元分析方法具有计算速度快、结果简洁易分析的特点，其主要操作步骤如下。

（1）将连续模型离散化为有限数量的简单单元，将盘参数化为具有质量和转动惯量的参数节点。定义每个单元节点，用节点位移表示单元中任意一点的位移。当1 个系统有N个节点时，元素为N-1 个。节点的广义位移为

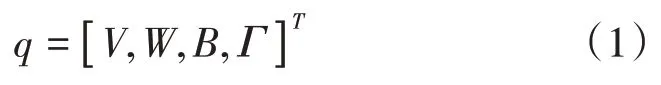
式中：V和W为节点的位移；B和Γ为轴在节点处的转角[8-9]。

（2）通过数学推导获得各单元的动能和势能表达式，利用拉格朗日方程得到各单元的运动微分方程；装配单元体矩阵，最终得到系统运动微分方程

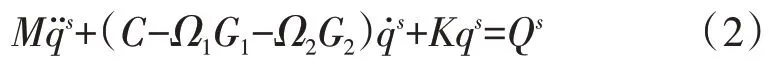
（3）通过求解式（2）得到系统各阶临界转速和相应的模态振型[10]，最终得到节点广义位移1维数组

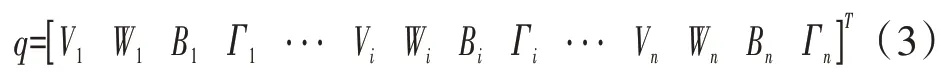
1.2 动力学相似理论

转子动力学相似一般包括固有频率、模态振型和特定状态下的不平衡响应（根据情况要求应变能分布相似）。单转子系统的基本动力学特性可以由复数微分方程[11]

为了保证式（6）始终成立，左、右部分的实部和虚部的系数应相等，即

得到与转子动力学相似的4个基本公式

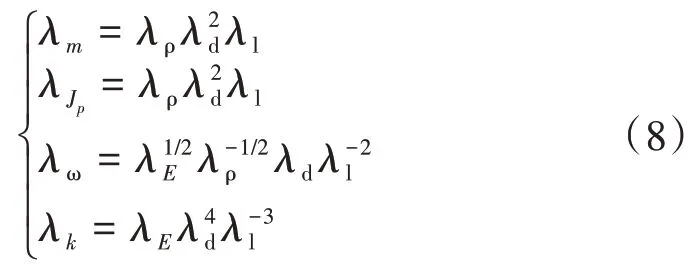
为使双转子系统中的燃气发生器转子和动力涡轮转子正确耦合，首先应保证模型双转子系统各阶固有频率与原型转子系统的各阶固有频率比相同。

此外，对双转子系统必须在2 个转子耦合的节点拥有相同的挠度。本文的双转子系统应在轴承共腔结构外传力框架处具有相同的挠度。偏心量相似比与其他参数相似比之间的关系为

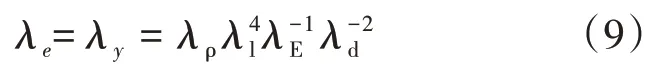
2 畸变模型的相似优化

在理想条件下，根据动力学相似理论建立的模型转子在临界转速相似比和模态振型方面应与原型转子完全相似。然而，这种相似模型在实际工程应用中无法实现，因为在实际工作中总是因为标准件或加工原因存在设计畸变。 因此，本文基于实值遗传算法提出了1种优化模态参数（m,l,d,ρ,E）[12]的优化算法。

（1）模态振型置信度MAC。模态振型置信度（Modal Assurance Criterion）是对2 种模态振型一致性的度量[13]，定义为2个模态振型的夹角余弦值的平方

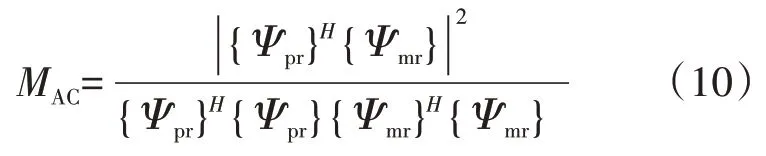
式中：ψpr为原型转子系统第r阶模态的振型；ψmr为模型转子系统第r阶模态的模态向量。

多模态振型置信度MCO（Coordinate Modal Assur⁃ance Criterion）是模态保证准则的扩展，综合反映了多阶模态的模态振型的总体一致性

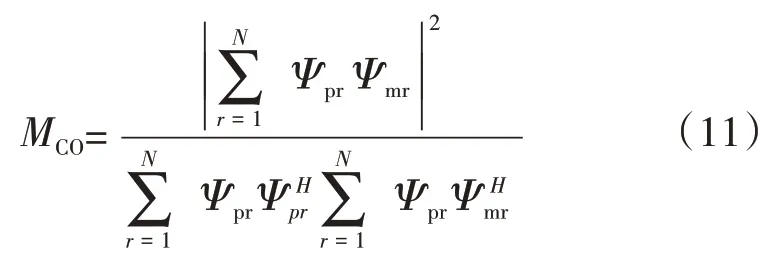
（2）遗传算法优化。为了控制相似模型转子的相似质量，在相似模型的设计优化中引入了多岛遗传算法（Genetic Algorithm）。在本文中采用实数编码遗传算法对转子参数值进行直接优化，无需将转子的实值参数转换为浮点数，更加直观易于操作[14]。

通过多岛遗传算法进行相似度优化。首先，将带有畸变的原始相似模型的所有可优化变量参数构造成1 个数组，作为初始个体，见式（12）。其次，通过对初始个体中的参数进行上下浮动构造搜索空间并在搜索空间中随机生成大量的转子模型，将随机生成的转子模型分组处理形成几个初始种群。再次，对初始种群中的1 维转子模型批量进行有限元分析得到每个转子对应的临界转速和模态振型，进一步计算适应度。执行遗传算法标准的选择、交叉和变异操作，获取新一代的种群。重复这些过程以获得总体相似质量更好的种群。最终选择最后一代种群中适应度（即相似质量）最好的个体。

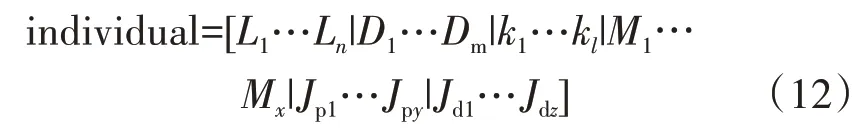
式中：n、m、l、x、y、z为各种可变参数数量。

采用实值遗传算法优化转子的算法结构流程如图1所示。

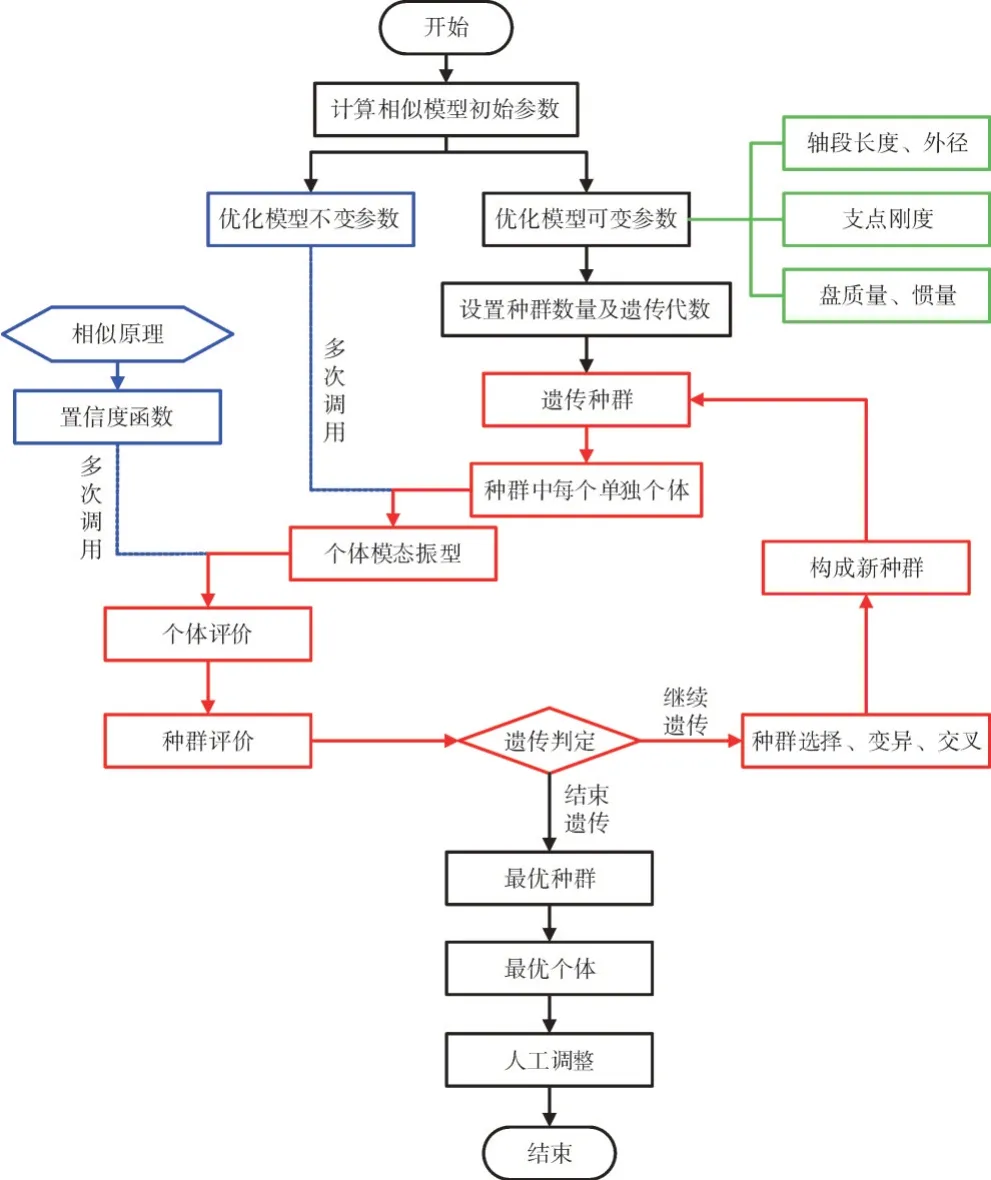
图1 遗传算法相似优化流程

在遗传算法中最关键的步骤是对个体的适应度评价，构造合适的适应度函数能够确保算法能够筛选掉不合适的转子模型留下更为相似的转子模型。

为了保证相似模型与原始模型具有相同的转子动力学特性，2 种模型的模态形状应高度相似。与单转子系统的类似工作不同，为了保证双转子系统的适当耦合，功率涡轮转子和气体发生器在任何时候都应该处于相同的状态，意味着双转子的临界速度应该成正比。因此，适应度函数应该至少是MAC（或MCO）和临界速度的组合。计算结果表明：在考虑多阶振型（大于4）的情况下，利用MCO建立适应度函数的效果不理想。原因是MCO包含了太多的阶次模态向量信息，缺乏重点，经常存在某1 阶模态的MAC较低而MCO较高的情况。因此，推荐MAC的适应度与临界速度的惩罚函数相结合，由不重要模态向重要模态依次进行单阶优化。

为衡量临界转速与目标临界转速的偏差值，设计临界转速罚函数

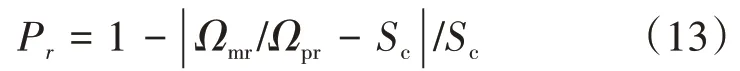
式中：Ωpr、Ωmr分别为是原型、模型转子的第r阶临界转速；Sc为设计目标中的临界转速相似比。

结合MAC值和临界转速罚函数的的适应度值为

为了提高优化算法的执行效率，本文采用了动态代沟（筛选比例）的筛选策略。在开始以较高的淘汰率来缩小搜索区域，然后以较低的淘汰率进行精细优化。本文设计的代沟函数为

式中：n为单个世代所有种群中个体（模型转子）的数量；Fitnr为这一代模型群中个体的最高适应度。

在本文中，交叉算子设置为0.7，变异算子设置为0.1，均保持不变。

3 原型转子和目标模型转子

原型涡轴发动机是双转子系统，2 个转子旋转方向相同，结构如图2 所示。转子系统有6 个轴承。动力涡轮转子是支撑在1、2、5、6 号轴承上的悬臂转子，燃气发生器是支撑在3、4 号轴承上的简支转子。轴承4～6安装在轴承共腔结构过渡段中。燃气发生器与动力涡轮通过轴承共腔结构耦合振动。

图2 原型发动机转子模型

轴承共腔结构安装在柔性的涡轮导向器上，动力涡轮转子和燃气发生器转子的振动耦合特性可以通过调整共腔结构参数进行调整。

由于试验转子的燃气发生器采用空心电机驱动，动力涡轮转子与燃气发生器无法保证相同的长度相似比如（图3）所示。为使空心电机有足够安装空间，动力涡轮转子和燃气发生器上应采用不同的目标相似度。

图3 相似目标模型

4 有限元建模和相似性设计

4.1 建模与相似性设计

由于后续的遗传算法优化步骤需要进行大量的转子动力学分析，因此用1 维有限元方法分析原型转子的动力学特性。将原型转子的3 维转子模型离散为具有79个节点的1维模型。其中，动力涡轮转子有38个节点，燃气发生器转子有36个节点，其余节点为轴承共腔结构模型。动力涡轮通过5、6 号轴承连接到共腔结构过渡段，燃气发生器通过4 号轴承与共腔结构过渡段连接。共腔结构过渡段可被视作支承在一弹性支承系统上，该支承系统由1 个径向弹性支承和1个角向弹性支承以及对应的阻尼器组成。

本文设计目标转速相似比设置为0.3，动力涡轮尺寸相似比设置为1.7。为方便比较模型转子和原型转子之间的差别，相似模型转子的1 维参数节点数与原型转子保持一致。相似工作转速覆盖经相似比换算后的原型转子的工作转速。

考虑到加工和材料性能，相似模型转子不能理想地与原型转子相似。因此，通过相似原理直接得到的转子模型需要经过可行化调整后才可加工。

本文相似比例模型的畸变主要来自以下几方面。首先，原型转子盘是不规则盘，在相似比例模型中被转换为同重心位置处的规则转子盘。 其次，由于受加工条件限制，将原型转子动力涡轮的空心轴改为普通轴。再次，弹性支承为防止失稳的刚度不能无限减小。此外，还有因材料属性限制和封严件等小结构差异造成的非人为畸变，将畸变设计于初始比例模型，构造出原始的畸变模型。

此时，畸变模型的模态振型和原型转子的模态振型产生了一定偏差，需要优化转子的振型和应变能参数才能达到相似要求，本文采用遗传算法进行优化。

首先将待优化参数形成1个数组，并根据参数类型给出上下界。 使用第2 章中提到的遗传算法方案对畸变模型进行优化，并对畸变模型转子与原型转子之间的振型置信度进行优化，如图4 所示。考虑前4种自激模态（前2 阶动力涡轮转子模态和前2 阶燃气发生器转子自激模态），优化前后模型转子的振型置信度至少增加了14%。其中动力涡轮转子第2 阶振型置信度值较低（93%）是因为该阶模态为动力涡轮转子弯曲模态，在工程设计中动力涡轮刚度畸变较大，给出的设计限制无法满足更高的振型相似度。

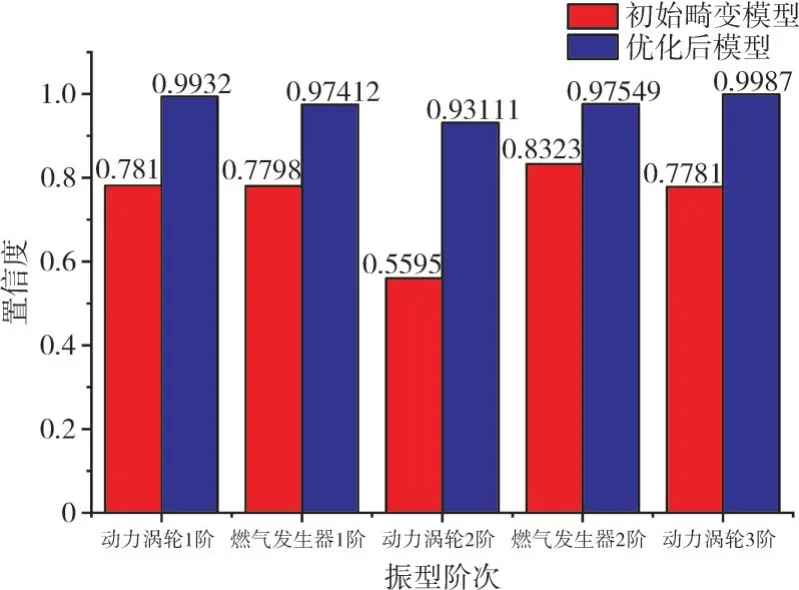
图4 振型优化效果

4.2 结果与误差分析

分析原型转子和模型转子的振型，各阶模态振型如图5所示。左列为原型转子振型，右列为模型转子振型。

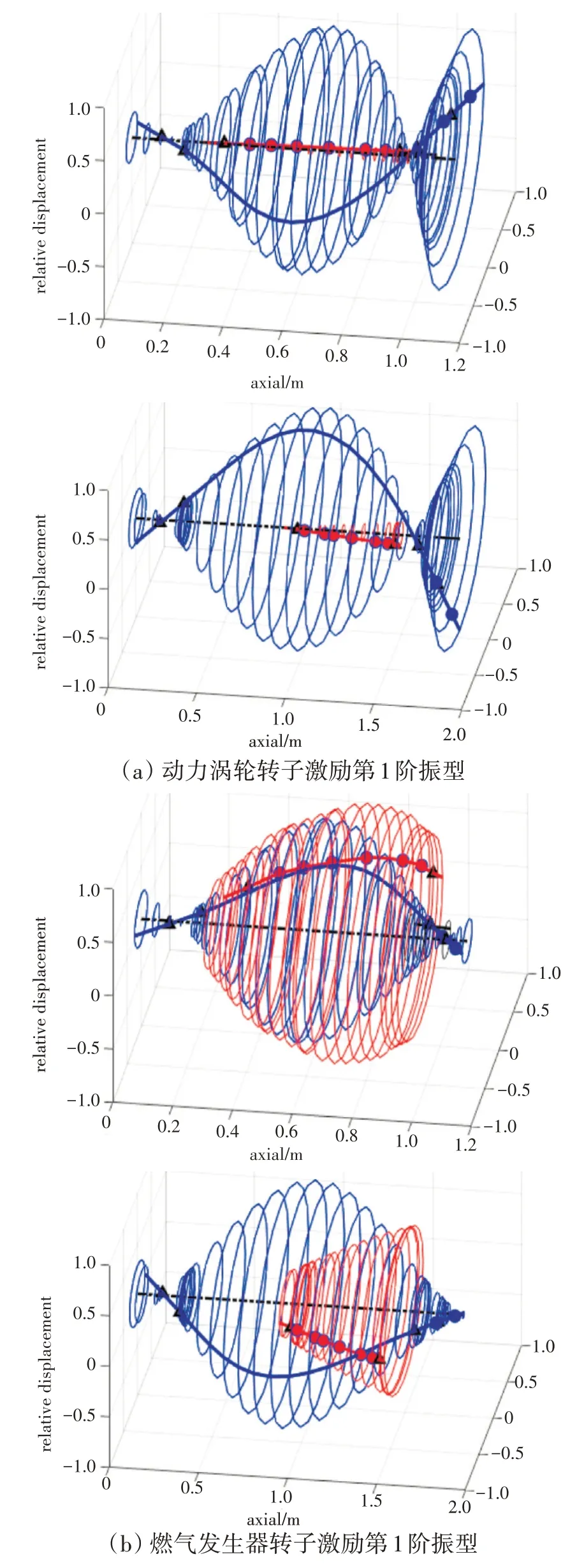
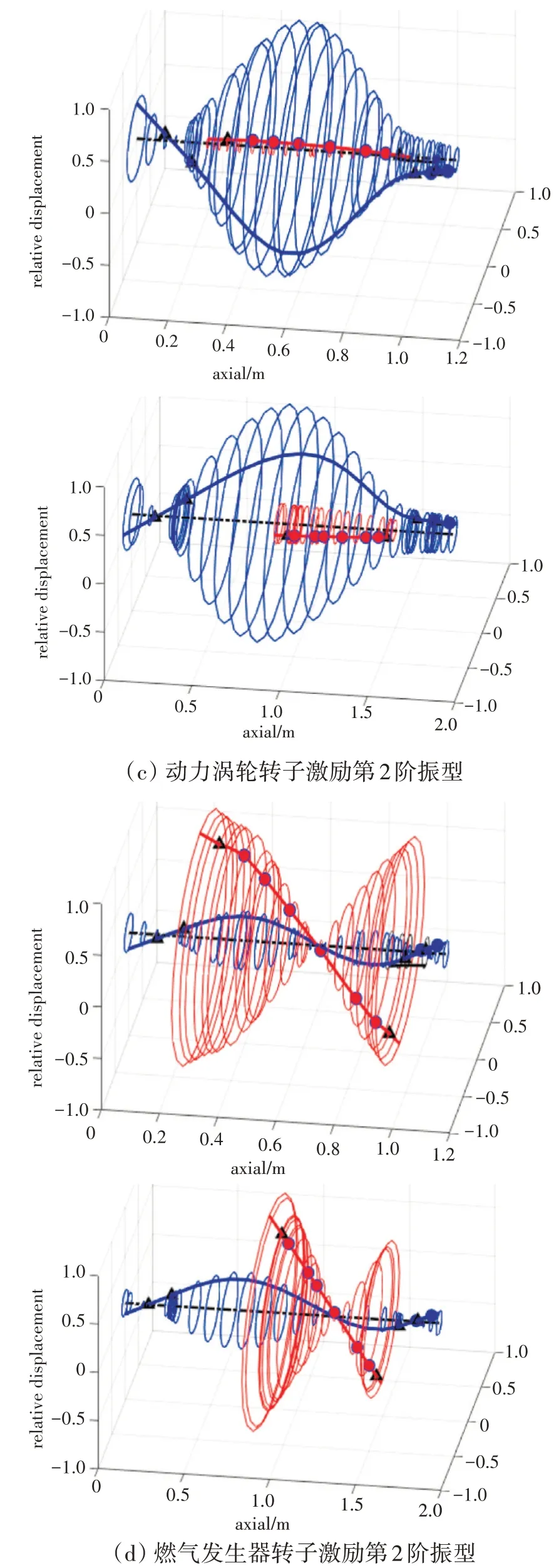
图5 计算振型对比

从图中可见，相似模型转子的动力涡轮转子振型与原型转子具有较高的一致性，而燃气发生器转子振型比原型转子更加平直，这是在加工时人工调整的。在设计中仍然保证了轴承共腔结构内的3 个轴承偏心率成比例，这意味着动力涡轮转子和燃气发生器转子之间的耦合正确性得到了保证。

原型转子和模型转子的临界转速见表1。从表中可见，相似模型转子的临界转速相似比得到了良好地控制。

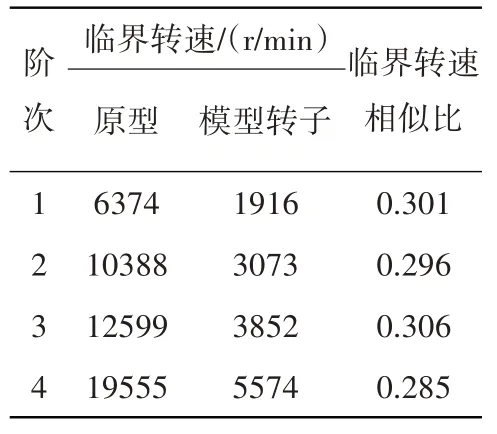
表1 原型转子和模型转子临界转速对比

在相同不平衡量作用下，相同结构的对转双转子不平衡响应较同转双转子更为显著[15]，这种响应差异主要来源于陀螺力矩的不同，相似转子的陀螺力矩也是相似的。因此，本文仅讨论动力涡轮转子和燃气发生器转子同转情形下的不平衡响应情况。模型转子和原型转子在动力涡轮2 个典型位置处的不平衡响应如图6~9所示。上方是原型的不平衡响应，下方是相似模型转子的不平衡响应。从图中可见，不平衡响应峰值出现的转速值成比例。响应峰值高度和宽度不同是因为2 种模型的不平衡量和阻尼并未设置在同一相似比上。

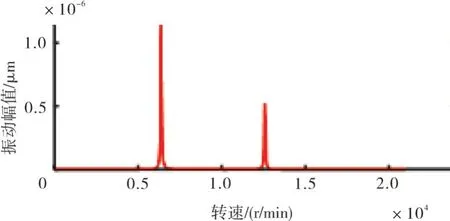
图6 原型转子动力涡轮轴中央同位置不平衡响应

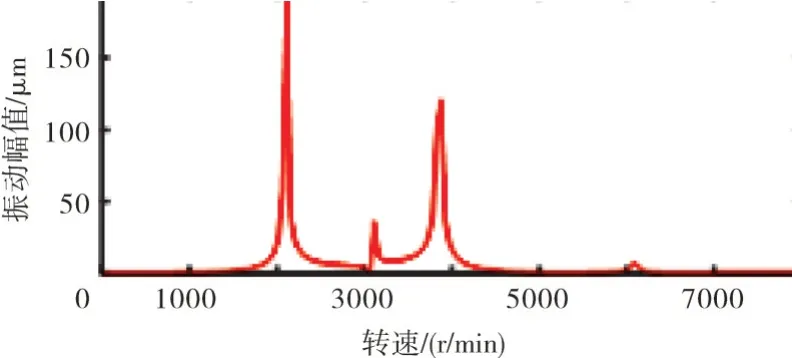
图7 相似模型动力涡轮轴中央同位置不平衡响应

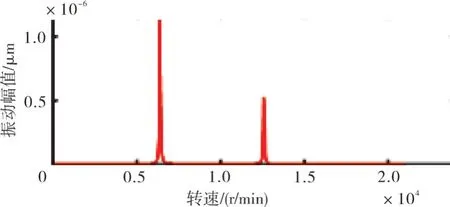
图8 原型转子动力涡轮第2级盘处不平衡响应

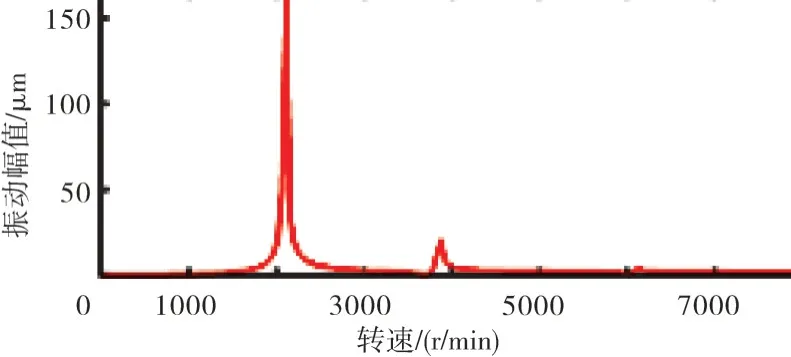
图9 相似模型动力涡轮第2级盘处不平衡响应

5 结论

本文以一种轴承共腔结构双转子涡轴发动机为研究对象，开发了1 套动力学相似设计和优化方法，并用该方法建立了与该型发动机动力学相似的双转子试验器模型。讨论了轴承共腔结构双转子系统在2 个转子具有不同相似比下的设计方法，通过保证挠度的方法让双转子正确耦合。

以有限元算法和多岛遗传算法为基础建立了轴承共腔结构双转子系统的相似设计方法，建立了基于临界转速和振型置信度的相似质量衡量指标函数即适应度函数。经轴承共腔结构发动机模型验证，采用该方法优化后双转子系统的振型置信度MAC可以达到0.8 以上，临界转速相似比具有较好的一致性。该方法理论上可以推广至其它转子系统的动力学相似工作中。