改进的WKNN算法研究*
2021-07-20徐锦修韩雨辰刘清华
徐锦修,仲 臣,韩雨辰,刘清华
(安徽理工大学 空间信息与测绘工程学院,安徽 淮南232001)
随着社会信息化、科技化,美国的GPS,中国的BDS等室外定位导航系统已经取得了显著进展,技术也比较成熟。研究表明,人们有超过80%的时间在室内活动,并且最近市场对大型室内环境特定的位置感知内容的兴趣有所增加,例如大型购物中心,博物馆,展览中心以及机场等大型公共场所,人们对室内定位技术产生了浓厚的兴趣,对于提供精确的室内位置信息将对生产生活产生重要的意义。在室内环境下,卫星信号是无法穿透墙体的,GNSS技术也没有办法在室内进行定位,由此看来,室内现在已经成为了卫星定位系统的盲区。因此,室内定位技术的研究和发展已经变得尤为重要。我国现阶段应用比较多的定位技术主要有蓝牙定位、惯性导航、WiFi定位、地磁定位等。蓝牙室内定位技术的原理是通过采集信号强度来定位。蓝牙具有存在体积小,低功耗并且容易部署的优点,但是又存在通信距离短,受噪声的干扰较大以及信号稳定性不好的限制[1]。惯性导航的定位原理是通过惯性传感器获取的定位目标的加速度,角速度等运动状态数据,推算出目标的运动轨迹[2]。其中,因为WiFi网布置简单,价格也比较低廉,并且广泛应用在室内环境中,现在已经成为一种普遍适用的定位方法。目前室内定位导航系统基本上是通过临近探测、指纹、多边定位或三角定位法来实现。
本文主要讲述的是目前国内外室内定位的现状,其次介绍了目前我国使用较为广泛的KNN、WKNN算法,并将其与改进的WKNN算法进行比较,其中,改进的WKNN算法也是本文的重点。
1 室内定位国内外现状
在文献[3]中,张媛等人分别对最小均方差估计算法,指纹估计算法及加权质心估计算法进行视距、非视距场景分析,并在此基础上建立了更高精度的测距模型,将基于UWB的指纹估计算法引入室内定位。在文献[4]中,陈良等人提出了一种优化人工神经网络的方法,即粒子群优化算法,用此算法来解决射频识别汽车室内定位在复杂环境下无法建立信号强度值和传播距离之间的映射模型问题。使用粒子群优化算法可以有效避免人工神经网络陷入局部最优等缺陷,建立一个准确的RSSI和标签位置的分类模型。在文献[5]中,单超颖等人针对神经网络参数不准确、室内环境复杂多变、无线信号的时变性以及支持向量机的定位性能不高等问题,提出了依据和声搜索算法对RBF神经网络进行优化的无线网络室内定位系统,可以有效提高室内定位的准确性。在文献[6]中,蔡金洋等人设计的基于扩展卡尔曼滤波的WiFi/PDR融合室内定位系统有效降低了室内定位的成本,提高了室内定位的精度,此方法的创新点在于对不易测量的噪声参数的自适应处理。在文献[7]中,徐德昌等人提出的基于萤火虫散发优化粒子滤波的行人航位推算融合地磁匹配的室内定位方法相较于传统的PDR算法,大大降低了计算量,更重要的是此方法有效提高了定位精度。
2 邻近算法介绍
2.1 KNN算法
K近邻算法是近邻算法的发展和延伸[8],为了改进NN算法中确定定位目标位置方法的缺陷,KNN算法利用公式(1)计算出定位目标与各个参考点之间的指纹相似度,并将其值按照升序排列。
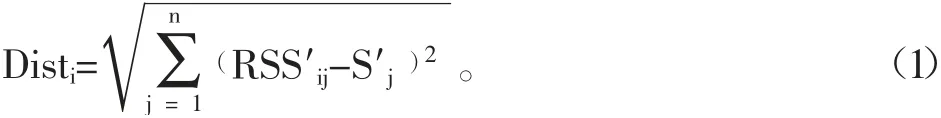
定位目标的K个最近邻参考点应选取前K(K≥2)个值对应的参考点,将这K个参考点所对应的坐标取平均值,进而估算出目标点的大约位置。
假设距离目标点最近的K个参考点的集合为{B1,B2,…,BK},这K个参考点对应的坐标分别为:
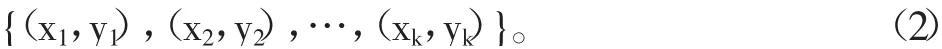
那么目标点的位置就可以根据公式(2)计算得到:

其中,(xi,yi)表示选取的K个近邻参考点中的第i个参考点的坐标。KNN算法相较于NN算法而言,它选用了更多的近邻参考点来确定目标点的位置,因而大大降低了定位的误差。通过使用该算法可以提高定位精度,降低室内定位技术功耗,而且不增加额外成本。尽管如此,目前KNN算法仍然面临着严峻的挑战[9]:
(1)空间歧义性:与当前位置相比,某些物理上遥远的位置可能具有相似的指纹或者相似的指纹距离,这可能会使KNN算法产生更大的误差。
(2)RSS不稳定性:运动的物体、周围的环境产生的电磁波不断变化,天线的方向性和射频干扰等,都会导致WiFi信号的大幅波动。因此在测试阶段采集到的某个位置的指纹可能与训练阶段收集到的指纹不匹配。
2.2 WKNN算法
WKNN算法对KNN算法进行了改进,在其基础上引入了权重的概念。由于WiFi的信号强度是随着距离增加而逐渐减小的,所以待测目标点与参考点之间的距离越大,参考点的信号波动就越强烈,对定位的作用就越小[10]。因此WKNN算法按照一定的规则对不同近邻参考点选取不同的权重来体现对定位作用的影响大小,近邻参考点与目标点的距离越近,那么它的权重就会越大,反之,则权重越小。离线阶段与在现阶段的定位如图1所示。
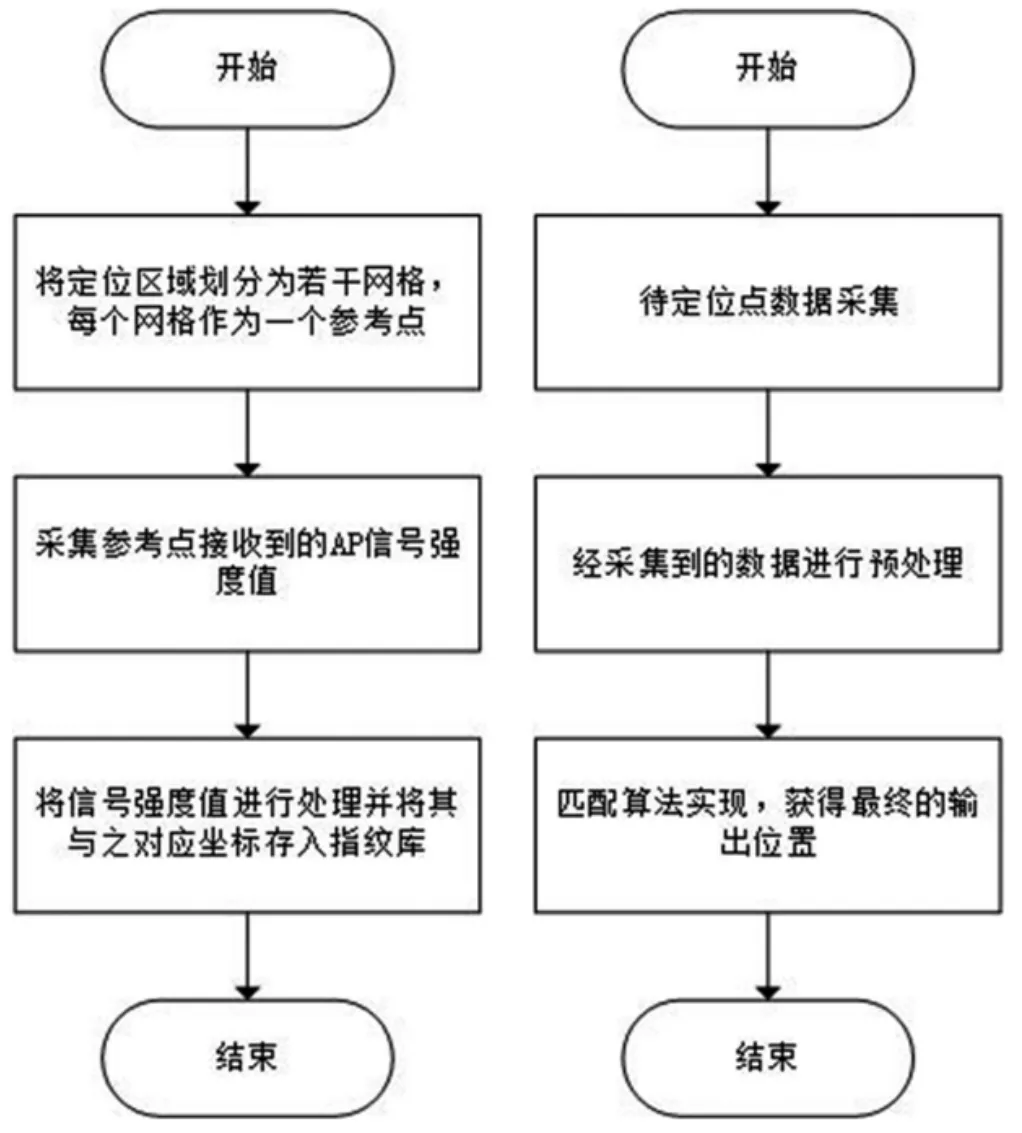
图1 位置指纹定位流程图
用WKNN算法进行定位,目标点的坐标可以根据公式(4)得到:
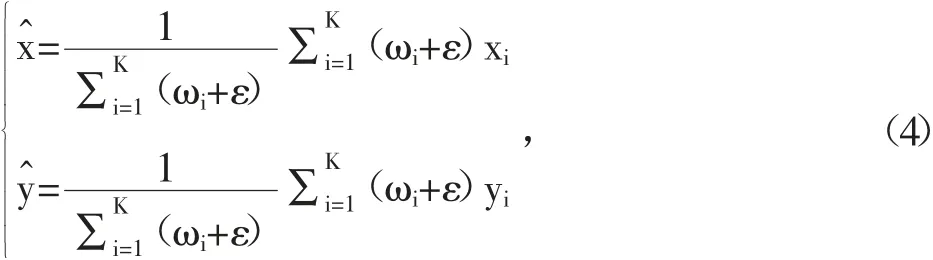
其中K表示的是最近邻参考点的个数;(x^,y^)表示的是定位目标的估计位置;ε是一个非零的数值较小的实数,它是用来避免出现ωi为0的现象,权重如公式(5)所示:

KNN算法和WKNN算法相较于NN算法在定位精度上均有所提升,但是选取的K值在多数情况下都是依靠经验判断的,不同的K值对试验的结果也会产生非常大的影响。而且KNN算法和WKNN算法在定位过程中计算量比较大,当在大面积区域进行定位时,定位结果显示会有很大延迟。
WKNN算法相较于KNN算法,其根据的K个最近邻参考点对定位的贡献程度,分配不同的权重,从而大大提高了定位精度。
3 改进的WKNN算法介绍
下面介绍的基于方差修正的WKNN算法可以减少上述的错误信号强度值对整体指纹距离的影响。用修正权重值di来表示每项实测值与存储值的差异量,大幅度修正信号强度值误差较大的,信号强度值误差较小的只需要进行小幅度的修正,具体的表达式见式(6):
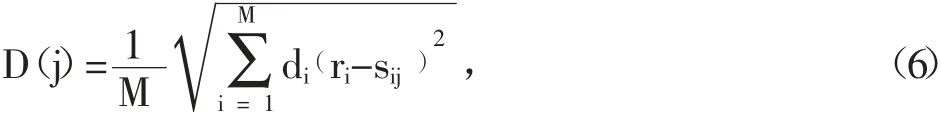
式中:D(j)-待测点相对于第j个离线参考点的位置;ri-定位阶段在待测点测得的第i个AP信号强度值;sij-离线阶段在第j个位置参考点测得并储存在指纹库里的第i个AP信号强度值。
由文献[12-13]可知,测得的某个AP信号强度值的均值Mean和方差Var存在着线性关系,如式(7)所示:

式中,将离线阶段该AP在全部参考位置点所测得的信号强度值,进行线性回归确定参数m和n的数值。
参考文献[12-13]可知,方差会随着信号强度的均值增大而减小,且该值的准确率也会随之提高。所以在参数m和n确定之后,可以将定位阶段中测得的每个AP信号强度值作为均值,也可以通过这个均值预估出所测得的信号强度的方差。最终结果会随着测量值的方差增大而减小,相应的测量值可信度也会随之降低。所以基本的修正权重可以用方差的倒数来表示。为了使得指纹距离D(j)中的权重值di之和为1,需要将权重值di进行标准化,公式参考式(8):

经过标准化之后通过指纹距离D(j)的大小筛选出K个近邻点。某一参考点的权重值是:该点指纹距离的倒数与K个近邻点指纹距离的倒数之和作比值,得到的结果即为该参考点的权重值,即
最后,将所求得的K个近邻点的坐标加权平均作为最终的定位结果。
4 实验与结论
将安徽理工大学义苑四号楼研究生公寓B区一层作为此次实验区域,该定位区域面积约为70m×20m的室内空间,公寓内有隔墙、桌椅以及走动的人员等干扰因素。此楼层设置20个采用TP-Link TL-WR840N型号热点的AP信号点。
首先把每个房间作为一个参考点,在每个参考点采集WiFi信号强度值,将每个信号强度值与对应坐标存入位置指纹数据库;其次在20个信号点中随机选取12个点作为测试点,记录每个点的实际坐标与各测试点的信号强度值;再采用KNN算法、WKNN算法以及基于方差修正的WKNN算法进行定位实验,将3种算法的定位误差取平均值进行比较,根据采集到的数据得到KNN、WKNN以及改进的WKNN算法对平均定位误差的影响,如图2所示。
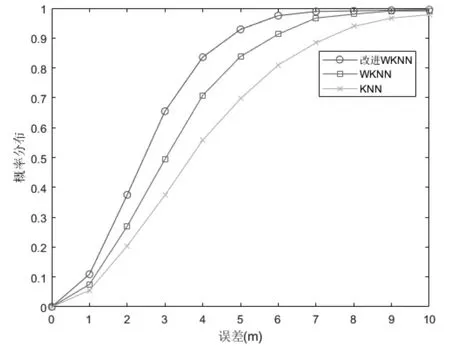
图2 定位误差对比
通过图2的对比数据可以得到3种算法的平均误差,结果如表1所示:
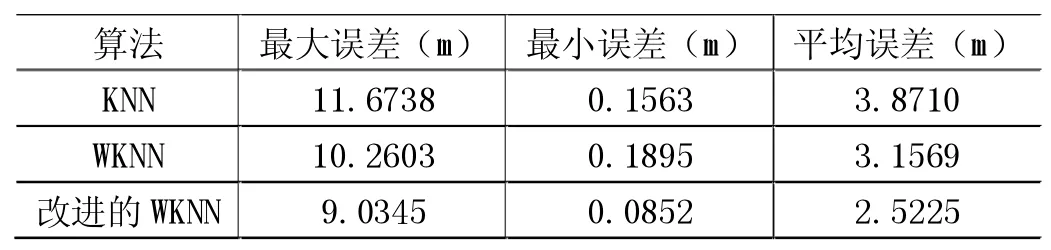
表1 3种算法的平均定位误差比较
通过图2可以看出,改进的WKNN算法的误差在7m左右基本没有太大变化,WKNN算法的误差9m以后没有明显变化,而KNN算法10m以前误差仍然比较明显。再结合表1,WKNN算法比KNN算法提升了18.48%,而改进的WKNN算法比WKNN算法提升了20.10%。对比图2和表1,改进的WKNN算法的平均误差明显得到了改善,因此改进的WKNN算法有效提高了定位精度。
5 结束语
当今社会互联网与通信技术不断提高,仅在室外进行定位已经满足不了人们日常的生活需求,因此室内定位技术由此出现并得到了迅速发展,并且室内定位技术极大提高了人们生活的便利性。本文主要讲解了KNN、WKNN算法的原理,分析了目前此方法存在的不足之处,并提出了改进的WKNN算法来弥补它们的不足之处,通过实验表明,改进的WKNN算法的平均定位误差比KNN和WKNN明显改善,因此改进的WKNN算法提高了定位精度。美中不足的是改进的WKNN算法的花费比较大,之后的研究要着重注意成本的问题。
