基于椭圆逼近算法的低通IIR滤波器设计与实现
2021-07-20李晴晴汤振华姜艳娜
李晴晴, 汤振华, 姜艳娜, 蒋 洁
(上海无线电设备研究所,上海201109)
0 引言
视线角速率是制导控制系统的一个关键指标。受系统内部噪声和复杂作战环境等因素的影响,导引头输出的视线角速率信号往往掺杂着许多高频噪声,不利于制导控制系统的平稳运行[1]。同时,由于制导系统实时性要求较高,因此需要设计一个快速响应的低通滤波器将高频噪声滤除。
经典的滤波器有无限脉冲响应(infinite impulse response,IIR)滤波器和有限脉冲响应(finite impulse response,FIR)滤波器[2-3]。IIR滤波器的输出不仅取决于当前和过去的输入信号,也取决于过去的输出信号。IIR滤波器传递函数的零点和极点位置可调,而FIR滤波器传递函数的极点固定在原点,只能通过改变零点位置来改变滤波器性能。因此为了实现较好的频率选择性,FIR滤波器相对于IIR滤波器,需要采用较高的阶数。针对相同的滤波器设计指标,IIR滤波器的阶数可能仅为FIR滤波器的1/5~1/10,因此更能够满足对视线角速率实时滤波的要求。
人们经过对滤波器的长期研究,已经形成了许多简单有效的逼近算法和精确的设计公式。目前常用的IIR滤波器有巴特沃斯(Butterworth)、切比雪夫(Chebyshew)、椭圆(elliptic)滤波器等。其中巴特沃斯和切比雪夫滤波器均可以通过限制椭圆滤波器的某些参数而得到。椭圆滤波器具有通带和阻带等波纹幅频响应的特性,它以通带和阻带的起伏为代价换取了更为陡峭的过渡带。对于给定的阶数和波纹要求,椭圆滤波器能得到较其他滤波器更窄的过渡带宽,可以获得对理想滤波器幅频响应的最好逼近,是一种性价比很高的滤波器[4]。故本文采用椭圆逼近算法设计低通IIR滤波器。
1 低通IIR滤波器设计原理
L阶低通IIR滤波器设计的本质是利用前L个输入x(n-L)~x(n-1)和当前输入x(n),以及前L个输出y(n-L)~y(n-1),通过加权求和获得当前输出y(n)。其设计原理可用差分方程表示为[5]
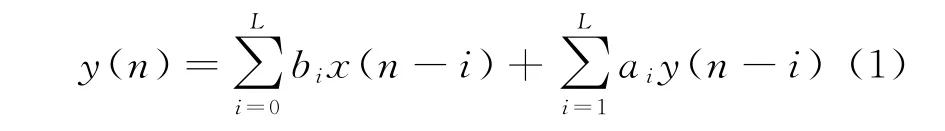
式中:bi和ai为差分方程待定系数。
将低通IIR滤波器差分公式进行Z变换,可得
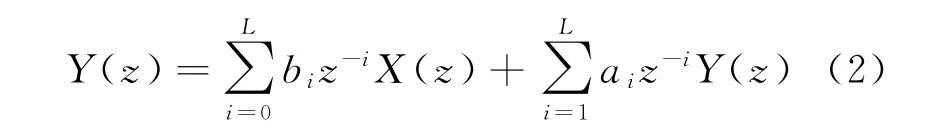
式中:Y(z)和X(z)分别为y(n)和x(n)的Z变换。
于是得到IIR滤波器的系统函数H(z),表达式为
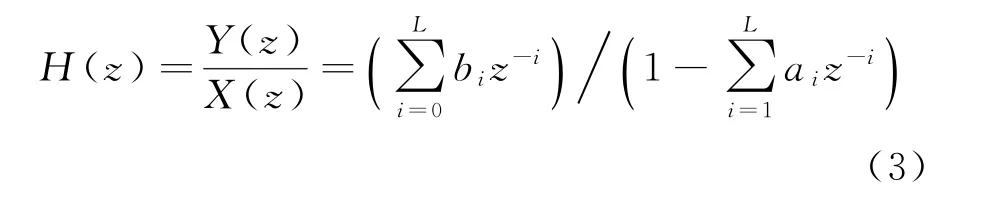
将式(3)进行图形化描述,可得到低通IIR滤波器的原理框图,如图1所示。
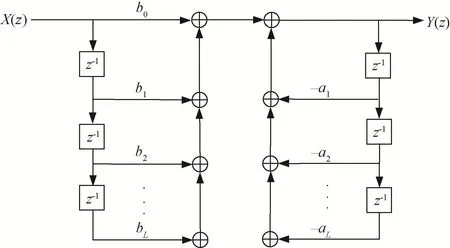
图1 低通IIR滤波器的原理框图
IIR滤波器系统函数H(z)在单位圆内的极点处出现峰值,在零点处出现谷值。因此IIR滤波器的设计就是要确定H(z)的系数bi和ai,以计算得到H(z)的零点和极点,使滤波器性能指标满足要求。IIR滤波器设计一般有三种方法:采用零极点位置累试法设计数字滤波器;借助模拟滤波器的理论设计数字滤波器;用优化技术设计数字滤波器。第一种方法的算法简单,设计粗略;第二种方法便捷高效,能较快得到理想的滤波器;第三种方法的设计步骤十分繁琐。因此,本文采用第二种方法设计低通IIR数字滤波器。具体可分为六个步骤:
a)采集多组输入信号,分析输入信号的幅频特性,总结得到设计要求;
b)确定一组滤波器的性能指标,包括采样率、通带截止频率fc、阻带截止频率fs、通带最大衰减Ap和阻带最大衰减As等,其中采样率应大于等于两倍通带截止频率fc,通带截止频率fc为输出幅值较输入幅值下降-3 dB时对应的频率;
c)根据滤波器的性能指标,采用椭圆逼近原理设计模拟滤波器的系统函数H(s)和阶数N;
d)进行仿真试验,验证模拟滤波器的滤波效果;
e)重复步骤c)和d),根据仿真结果适当调整模拟滤波器的参数,使模拟滤波器尽可能地逼近理想特性;
f)采用冲激响应不变法或双线性变换法,将满足要求的模拟滤波器的系统函数H(s)变换成数字滤波器的系统函数H(z)。
冲激响应不变法首先将H(s)进行拉普拉斯逆变换得到单位冲激响应h(t),对h(t)进行采样得到h(n),再对h(n)进行Z变换得到H(z)。由于数字滤波器的冲击响应是对模拟滤波器冲激响应的采样,因此该方法获得的滤波器时域逼近特性较好。
2 低通IIR滤波器设计仿真
为验证低通IIR滤波器设计方法的可行性,基于Matlab平台进行设计仿真验证[6]。设输入信号包含频率为10 Hz和100 Hz的正弦波以及高斯白噪声,输入信号的时域及频域特征分别如图2和图3所示。
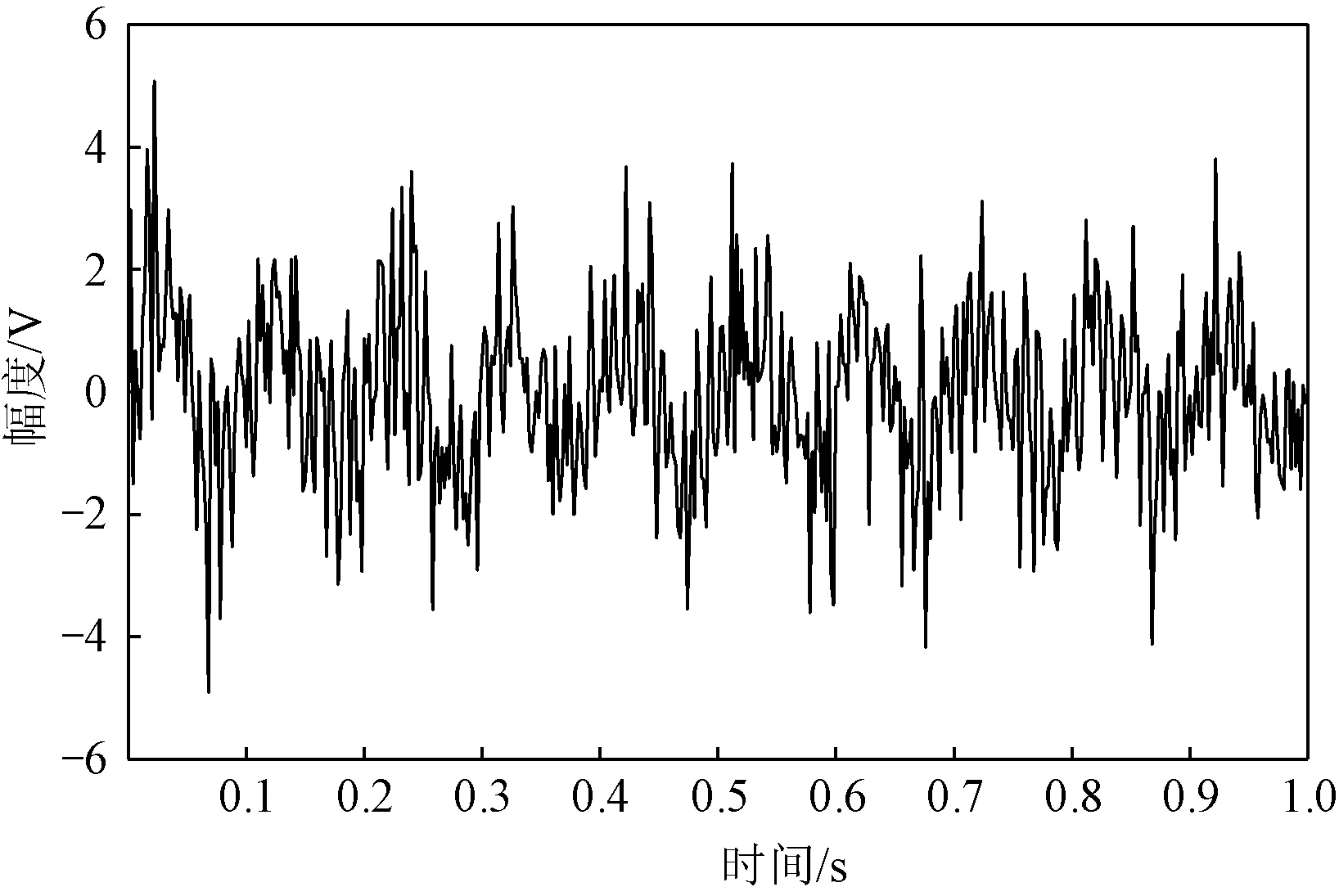
图2 输入信号时域图
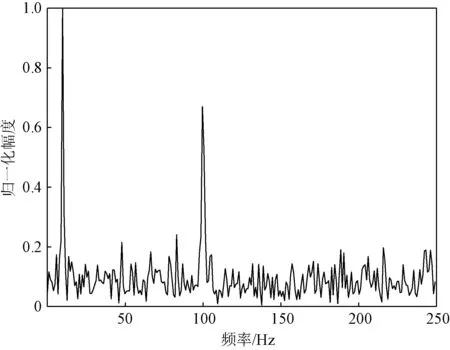
图3 输入信号频域图
为了滤除频率为100 Hz的信号分量,初步设定了一组滤波器参数[7]:采样频率1 000 Hz,通带截止频率20 Hz,阻带截止频率100 Hz,通带最大衰减0.05 d B,阻带最小衰减60 d B。
椭圆滤波器最小阶数N的计算公式为
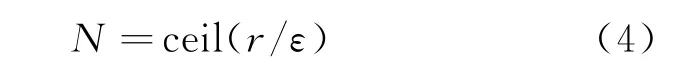
其中
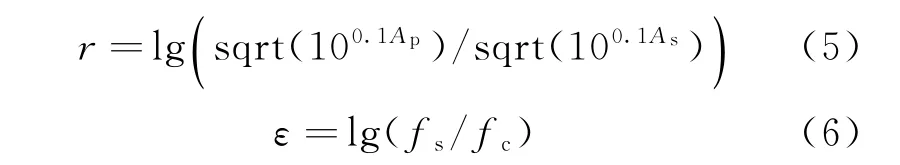
式中:ceil(·)为向上取整函数;sqrt(·)为开方函数。
通过计算得到椭圆滤波器最小阶数为6阶。结合IIR滤波器数学模型,根据式(1),采用双线性变换法可求解出IIR滤波器的系数,见表1。
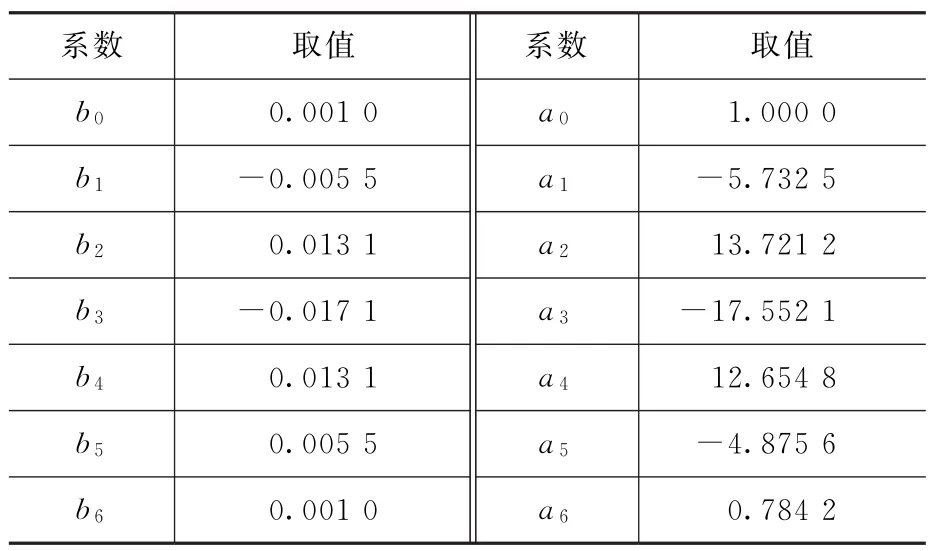
表1 IIR滤波器的系数
最终得到的椭圆IIR低通滤波器幅频响应如图4所示。
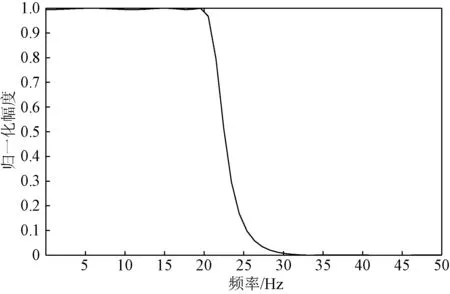
图4 椭圆低通IIR滤波器幅频响应曲线
采用上述IIR滤波器对输入信号进行滤波。输入信号与滤波后信号的时域与频域对比分别如图5和图6所示。
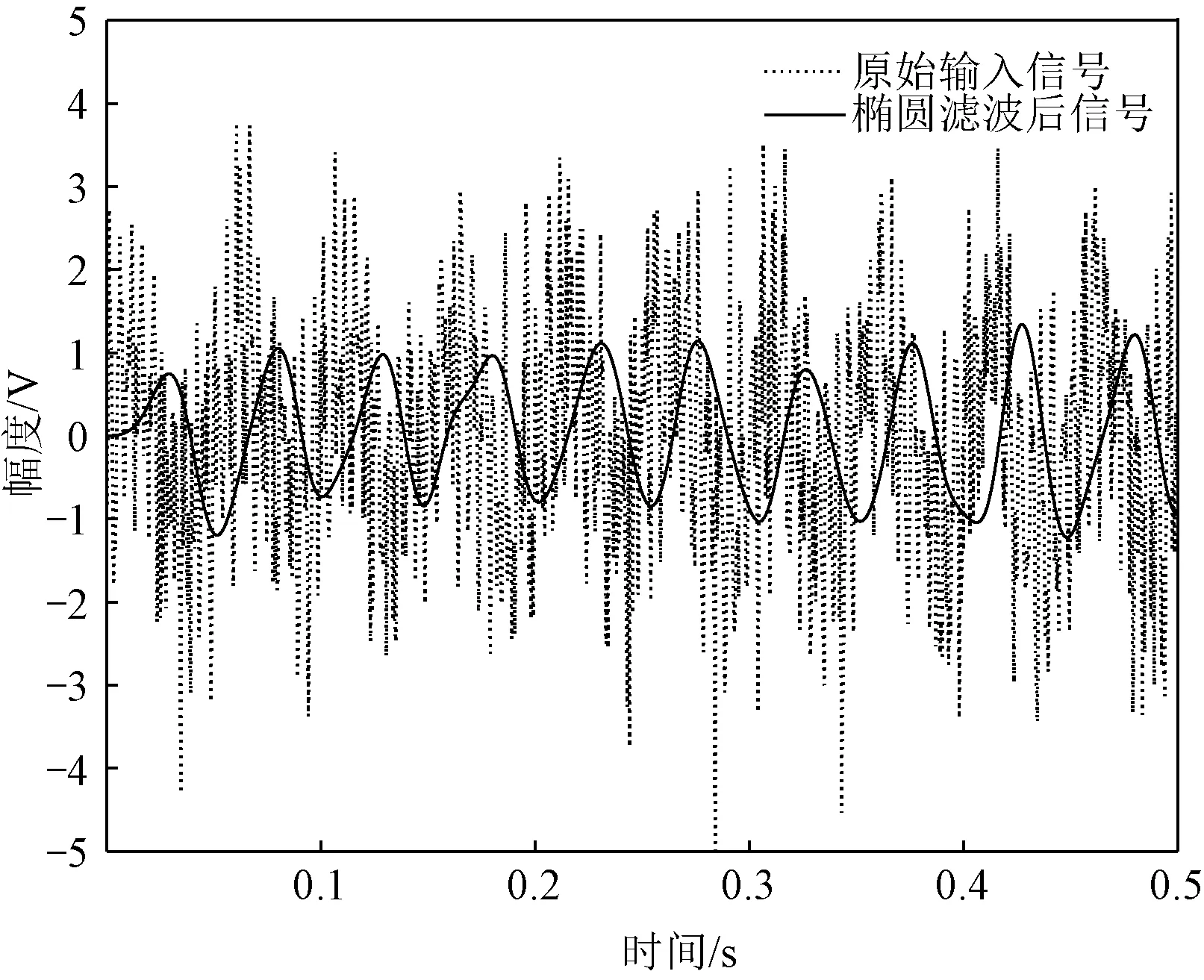
图5 输入信号与滤波后信号对比
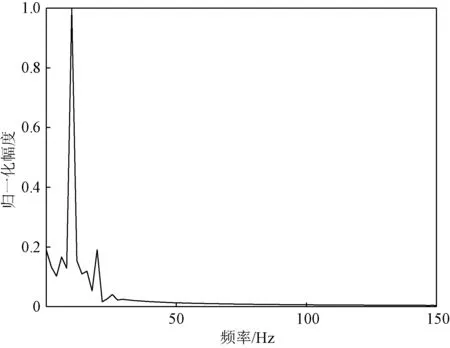
图6 椭圆IIR低通滤波器输出信号频谱图
从图5中可以看出,IIR滤波后的信号与原始输入信号相比存在一定的延时,延迟时间即为滤波器阶数与数据采样间隔的乘积,反映出椭圆IIR滤波器具有相位非线性。
从图6中可以看出,经过椭圆IIR低通滤波器后,输出信号中仅剩下10 Hz的低频分量,100 Hz的高频分量被滤除,实现了设计需求。
图7为相同参数下,6阶巴特沃斯IIR低通滤波器、切比雪夫IIR低通滤波器、椭圆IIR低通滤波器的幅频响应曲线。
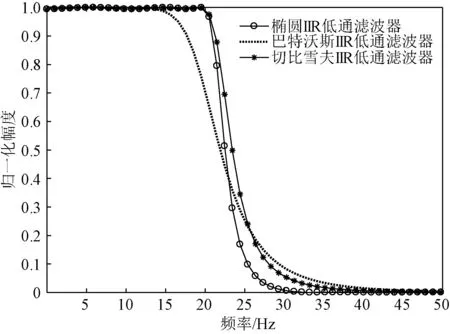
图7 6阶低通滤波器幅频响应曲线
从图7中可以看出,椭圆IIR低通滤波器的带外衰减速度最快,具有更好的频率选择性;切比雪夫IIR低通滤波器的衰减速度介于椭圆滤波器和巴特沃斯滤波器之间,且和椭圆IIR滤波器一样,在通带范围内具有波动起伏;巴特沃斯IIR低通滤波器虽然通带、阻带均无波动,但衰减速度最慢。综上分析,本设计中选用椭圆IIR低通滤波器。
图8为10阶巴特沃斯IIR低通滤波器、切比雪夫IIR低通滤波器、椭圆IIR低通滤波器的幅频响应曲线。
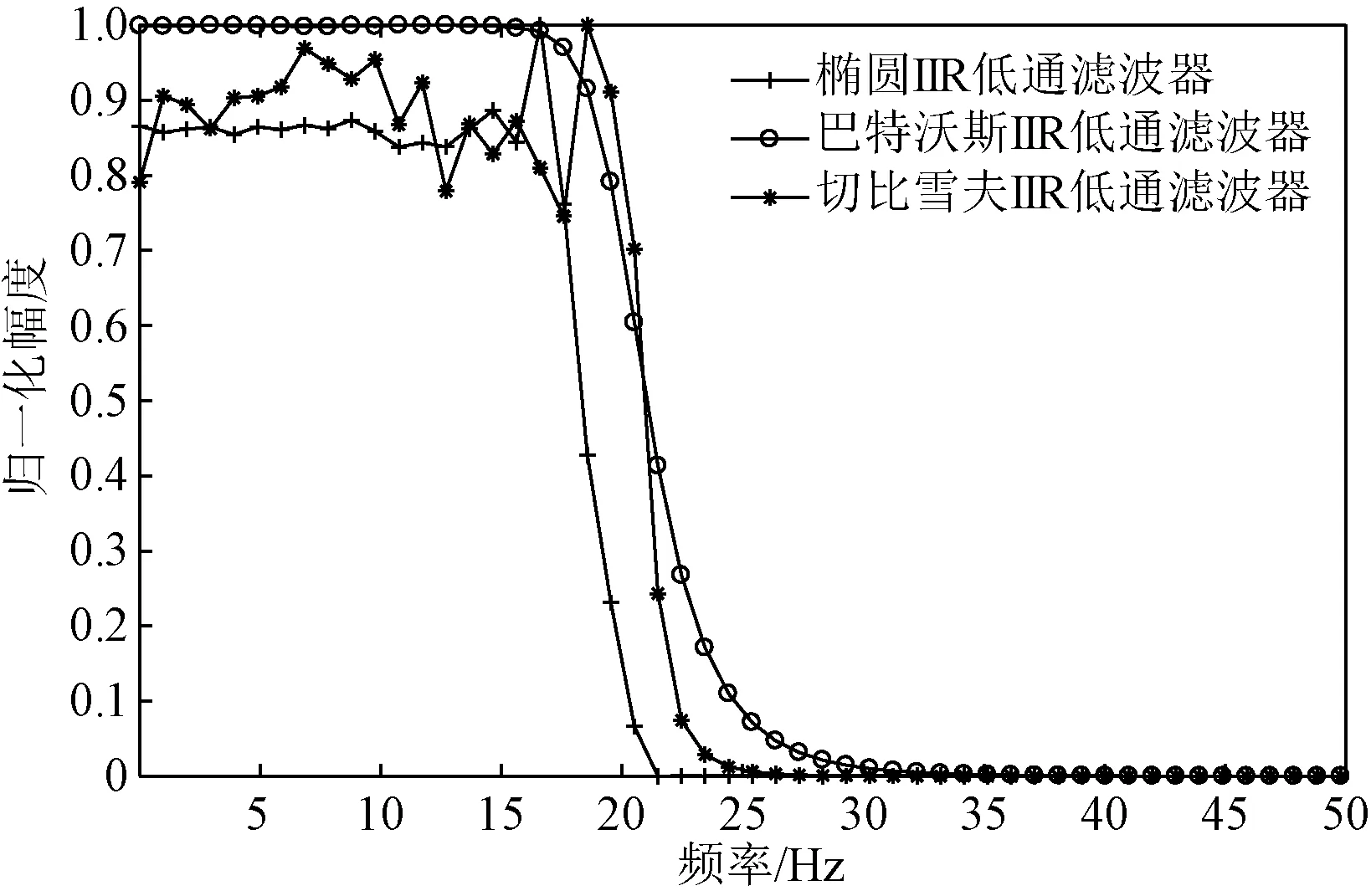
图8 10阶低通滤波器幅频响应曲线
对比图7和图8的仿真曲线,可知,随着阶数变高,椭圆IIR滤波器和切比雪夫IIR低通滤波器在通带内的波动幅度明显增大,输出幅度衰减也更严重。因此本设计中选用6阶滤波器。
3 实验验证
为进一步验证椭圆IIR低通滤波器设计方法的有效性,将该IIR低通滤波器移植到某制导控制平台上,实时采集不同环境下的视线角速率数据,当目标分别处于机动性较高、较低和静止三种状态时,观察该滤波器对输出视线角速率的滤波效果。
设定目标分别以10(°)/s和0.5(°)/s的角速率进行匀速往返运动以及处于静止状态,采集三组不同的实测数据,分别进行IIR低通滤波。三种状态滤波前后的视线角速率曲线如图9所示。
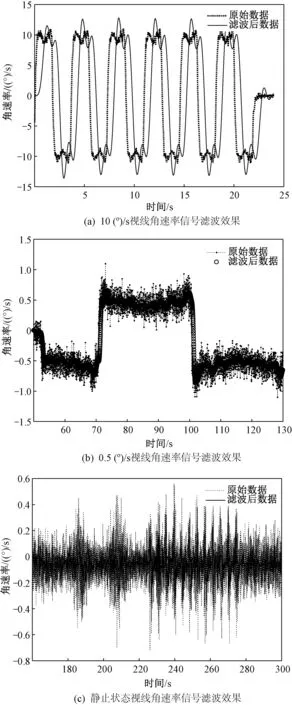
图9 某制导控制平台实验验证结果
为了更直观地分析滤波效果,计算不同目标状态下滤波后视线角速率方差相对于滤波前减小的百分比,得到三种不同目标状态滤波后视线角速率方差分别减小了14.84%、40.01%和48.80%。
根据上述实测数据的仿真结果以及数据统计结果可以看出,目标机动性能越小,IIR低通滤波器的滤波效果越好,尤其当目标静止时,视线角速率信号中的高频噪声经过滤波后幅度可以降低将近一半,能够有效地保证制导控制系统的可靠性和稳定性。
4 结论
选用椭圆逼近算法设计IIR低通滤波器,对导引头输出的视线角速率信号进行滤波。仿真结果表明,该滤波器在目标机动性较小的情况下,滤波性能较好,可以满足设计要求。
