紊流模型预测街道峡谷流场能力的定量指标评价

2021-07-20谢海英王晓晓曾天林

能源研究与信息 2021年2期

谢海英，王晓晓，杨怡，曾天林

（上海理工大学环境与建筑学院，上海 200093）

利用数值模拟法研究城市街区尺度的气流及交通污染物扩散问题时，选取合适的紊流模型是关键。雷诺时均模型将紊流中所有尺度的涡对时均流动的影响建模处理，LES (large eddy simulation)和DES(detached eddy simulation)模型则可直接模拟流动中的大涡而仅对小涡建模，因此，它们比雷诺时均模型更具有普适性。但LES和DES模型的计算成本远高于雷诺时均模型的，同时，由于模型本身的不完善性，它们的模拟结果有时也并不总是好于雷诺时均模型的，在需要快速给出流动情况时，雷诺时均模型仍然是工程上更受欢迎的选择。

然而，由于雷诺时均模型的普适性相对较差，其预测能力会随研究问题的不同而变化，因此，在模拟街区尺度的气流问题时，需比较各紊流模型的预测能力。已有研究大多根据数值模拟结果与试验数据的吻合程度对模型预测能力给出定性判断而缺少定量依据。因此，本文拟选用定量指标，采用定性与定量相结合的方法来比较各种紊流模型的预测能力，从而为优选紊流模型提供更合理的评价策略。

1 计算模型

本文利用Fluent软件，按水槽试验数值模拟高宽比为1∶1的城市街道峡谷（简称街谷）内的时均速度和脉动强度。图1为计算域设置及水槽试验测点布置。该试验中共有8个建筑物模型。建筑物高（H）、宽（W）和街宽（W）相同，均为0.10 m，建筑物长为0.30 m，水槽进口来流速度U为0.12 m·s。坐标轴x、y和z向速度分别为u、v和w。计算域进口距离第1个建筑5H，出口距离最后一个建筑15H，顶部距离池底4H。水槽试验的流场测点位于x向第4、5个建筑模型之间，且在y向的对称面上，其具体位置见图1(b)。测点所在的3条竖直线段依次命名为LL、 LM和LR，2条水平线段分别为LH和LT，共有近100个测点。

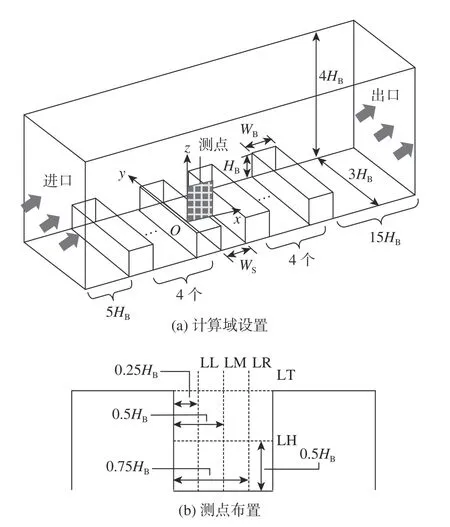
图1 计算域设置及水槽试验测点布置Fig.1 Computational domain and the layout of the test points in the water channel

计算域进口采用水槽试验的来流条件，出口采用出流条件，其余墙面为固壁边界，计算域顶部设为对称边界。利用商用软件ICEM生成结构网格，对壁面附近进行网格加密。经网格独立解验证，本文选用的网格数量约为 2.26 × 10。模拟的控制方程为连续性方程、Navier−Stokes方程和紊流模型方程。紊流模型分别选用标准k−ε模型、realizable k−ε模型、RNG k−ε模型和SST k−ω模型，各方程具体形式可参见文献［7］。近壁处采用标准壁面函数法处理，方程离散选用二阶迎风格式，计算收敛的标准为残差达到1.0×10，且流场无变化。

2 模拟结果与分析

2.1 模拟结果的定性评价

图2、3分别为采用4种紊流模型得到的时均速度和脉动强度模拟值与试验值的比较，其中u′、w′分别为x、z向的脉动强度。模拟时假设流动为各向同性紊流，由模拟得到的湍动能计算得到脉动强度。

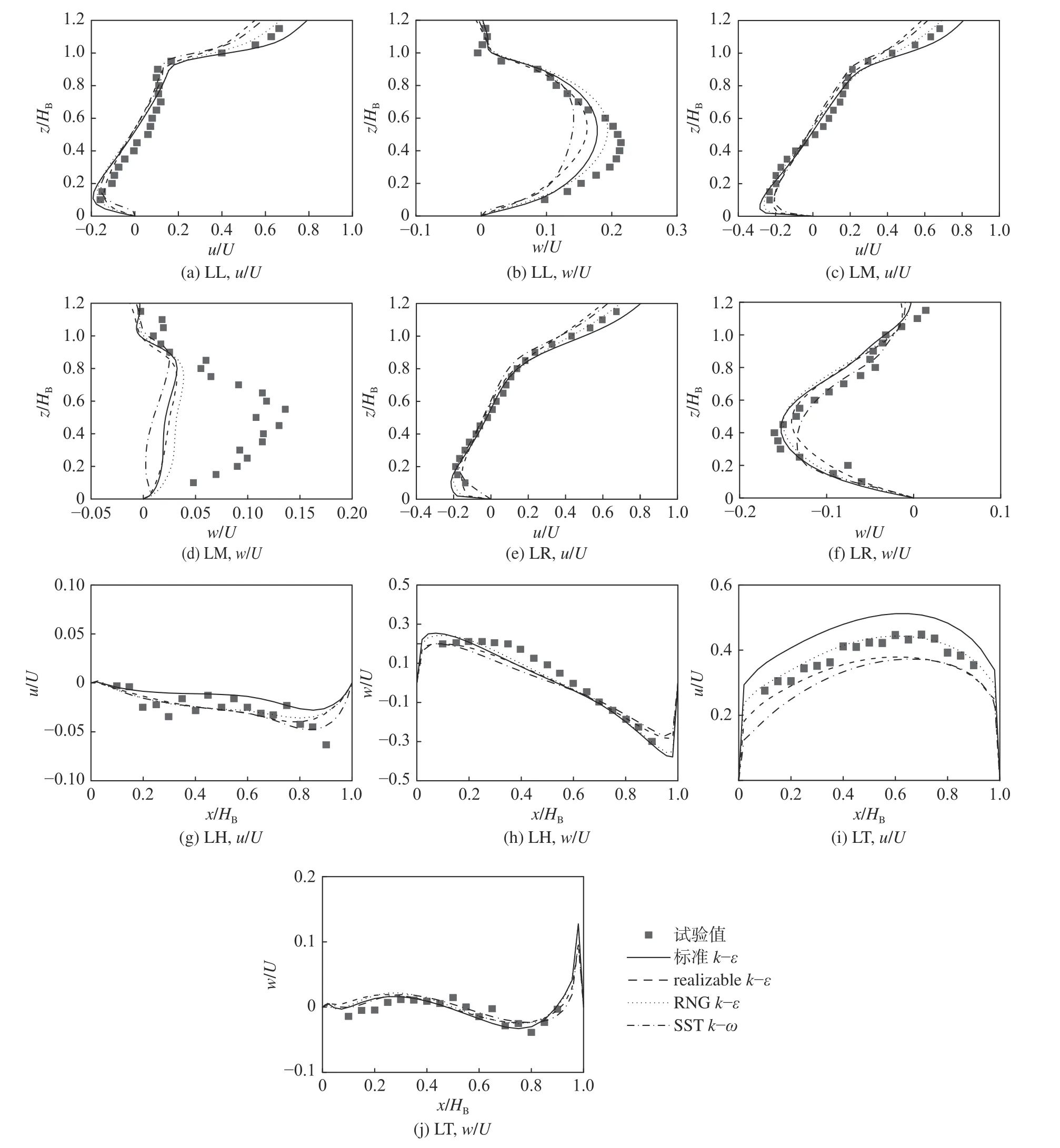
图2 时均速度模拟值与试验值的比较Fig.2 Comparison between the simulated time-averaged velocities and experimental values

由图2中可知，除了在LM处的w/U模拟值与试验值吻合情况不理想外，其余位置的时均速度模拟值与试验值吻合较好。由不同紊流模型得到的时均速度差别不大。在屋顶附近，标准k−ε模型的模拟值偏大，而realizable k−ε模型和SST k−ω模型的模拟值偏小，RNG k−ε 模型给出的模拟值相对较好。

由图3中可知，4种紊流模型的脉动强度模拟值在高出街谷顶部处偏大，街谷内的模拟值与试验值均吻合良好。这说明街谷内的紊流基本符合各向同性的假定，同时，各模型模拟值的差异也不显著。

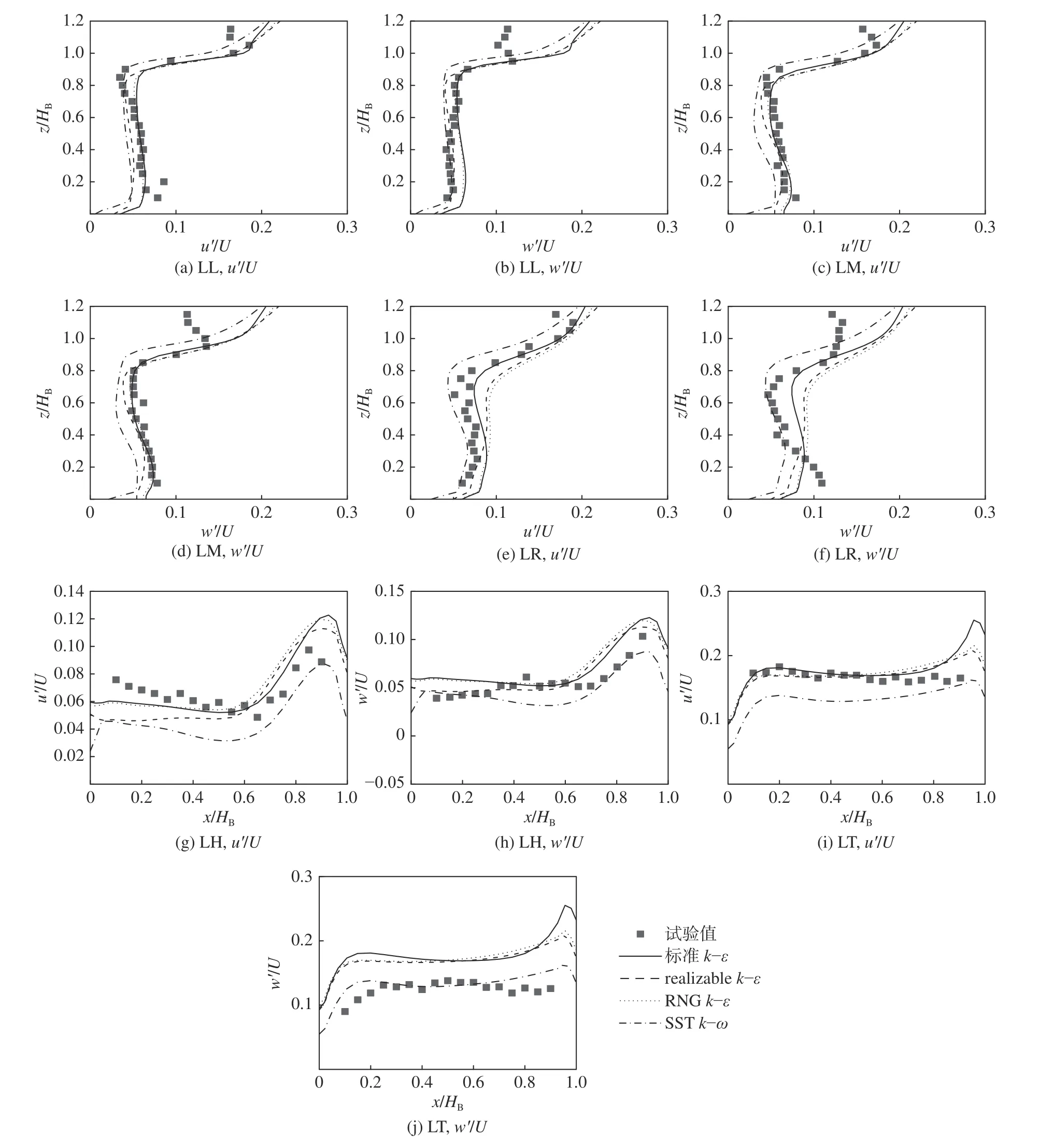
图3 脉动强度模拟值与试验值的比较Fig.3 Comparison between the simulated fluctuating velocities and experimental values

因此，根据时均速度和脉动强度模拟值与试验值的吻合情况，可定性判定RNG k−ε模型在大部分测点位置的预测结果较好，其余3种模型的预测能力差别不明显。

2.2 模拟结果的定量评价

为了定量评价不同紊流模型的模拟情况，本文参考文献［8–12］，定义了4个评价指标I、I、 I和I。

其中,

式中：a、 a分别为街谷内第 i 个测点处某变量的模拟值和试验值；N为总测点数； a和分别为某变量在所有N个测点上的平均模拟值和平均试验值；W为常数，值为0.05。

I反映了所有测点满足0.5 ≤ a/a≤2的情况，由于文献［6］未给出试验值的测量误差，当某些测点处的a接近0时，采用0.5 ≤ a/a≤ 2来衡量这些测点的预测情况不够合理，因此，取某个小值W，当∣a∣ ≤ W且∣a∣ ≤ W时，则n在该测点取1。为保证速度模拟值与试验值方向一致，还要求aa≥0。为描述方便，将上述情况简称为零值附近特殊处理法。本文也给出了不考虑零值附近特殊处理时的I（简称I）。参考I指标，本文还提出了I和I两个指标，即考察a满足0.8 ≤ a/a≤ 1.2的情况。显然，模型预测能力越好，I和I越接近1，I对模拟值与试验值的吻合质量要求更高，文献［8］中要求I＞0.5。

I和I均是统计a偏离a的程度量，模型预测越好，则I和I越接近0。I能从整体上考察a与a的偏离程度，但当a偏离a有正负且正负值大小相当时，需采用指标I，它能将所有a偏离a的程度累加而无论偏离的正负情况。一般要求−0.3＜I＜0.3，I＜4。

表1给出了4种紊流模型的6个定量指标结果。由表中可知，4种紊流模型均满足I＞0.50的要求。实际上，各模型时均速度的I＞0.80，紊流强度的I都接近或等于1，各模型的表现也无差异。由表1中还可看出，时均速度的I比I减小6%～10%，而脉动强度的指标值保持不变。

表1 4种紊流模型的定量评价指标
Tab.1 Quantitative evaluation indices for 4 turbulent models

指标 api标准k−ε realizable k−ε RNG k−ε SST k−ω IFAC2 u/U, w/U 0.82 0.81 0.83 0.82 u′/U, w′/U 1.0 1.0 1.0 0.99 IFAC2−NLV u/U, w/U 0.76 0.73 0.77 0.72 u′/U, w′/U 1.0 1.0 1.0 0.99 IFAC20%u/U, w/U 0.58 0.59 0.67 0.57 u′/U, w′/U 0.60 0.51 0.50 0.48 IFAC20%−NLV u/U, w/U 0.42 0.43 0.53 0.42 u′/U, w′/U 0.60 0.51 0.50 0.45 IFB u/U, w/U 0.014 0.38 0.16 0.45 u′/U, w′/U −0.15 −0.13 −0.18 0.14 INMSE u/U, w/U 0.30 0.48 0.19 0.62 u′/U, w′/U 0.080 0.094 0.095 0.094

然而，4种模型的I较I显著减小，时均速度和脉动强度的指标降幅分别为16%～25%和40%～50%。RNG k−ε模型在时均速度的I上表现得最好，其值为0.67，而紊流强度的I则是标准 k−ε模型的表现得最好，其值为0.60。各模型的表现有一定的差异，最好和最差的指标值之差约为10%，标准k−ε模型在时均速度和脉动强度上的I基本相同，另外3种模型的时均速度指标均略好于脉动强度指标。与I相比，时均速度的I减小约15%，脉动强度的I则保持不变。显然，I对模拟值与试验值的吻合度要求最高，只有RNG k−ε模型能满足该指标的时均速度和脉动强度均大于0.5的要求，而标准 k−ε模型对脉动强度的预测结果最好，SST k−ω模型则表现最差。

4种模型的I均满足要求，时均速度的I依然是RNG k−ε模型的表现最好，其次是标准 k−ε模型，SST k−ω模型的I相对较大。4种模型在脉动强度上的I上差别不大。

从表1中可知，SST k−ω模型和realizable k−ε模型的时均速度均不满足I＜0.3的要求，尽管两者脉动强度指标均表现较好。标准k−ε模型时均速度的I指标要好于RNG k−ε模型的，两者的时均速度和脉动强度的指标均满足I＜0.3的要求。

因此，综合以上6个指标的定量分析可知：RNG k−ε模型的综合表现最好，该模型的时均速度指标中I指标的表现次佳，其余5个指标的表现均为4种模型中的最佳；综合表现其次的是标准k−ε模型，该模型对紊流强度的预测结果表现最好，但时均速度的指标略逊于RNG k−ε模型；realizable k−ε模型表现一般，而SST k−ω模型的表现则相对较差。上述结论与文献［13–14］中的结论基本一致，而文献［11］在模拟建筑物绕流问题时选用了改良型的SST k−ω模型，这说明SST k−ω模型在模拟建筑绕流问题上的确有不足之处。