基于智能电网的电动汽车充放电分时电价及引导策略
2021-07-20蒋俊峰谭伦农纪棋彬
蒋俊峰,谭伦农,纪棋彬
(江苏大学 电气信息工程学院,镇江 212013)
随着全球经济持续发展,为缓解能源危机和环境污染问题,世界能源加快转型。目前,发电环节是能源消耗与碳排放最大的来源之一。因此,各国政府和企业通过采取转变发电方式等措施来降低碳排放。其中新能源发电前景广阔,以风能、光能为代表的清洁能源逐渐成为可持续发展的重要标志之一。根据相关权威机构预测,到2050年,世界范围内清洁能源占总能源的比例将过半。在将来的电力系统中,常规能源逐步被淘汰,高比例可再生能源成为时代的主流。高比例可再生能源发电接入电网将导致供求曲线的不稳定。与传统的汽油车和柴油车相比,具有绿色、环保、高效等优点的电动汽车逐渐成为市场上的宠儿,大有代替常规汽车的趋势。大规模电动汽车无序接入电网也将导致供求曲线不稳定。
然而,电动汽车的优势是可作为移动的储能装置经有序充放电能完美地消纳风能、太阳能等可再生能源,实现供求曲线的稳定。为引导电动汽车有序充放电来消纳新能源,实现供求曲线平衡,采用分时电价机制引导电动汽车用户有序充电。消费者在政府优惠政策和电力营销策略刺激下转向消费电动汽车。电动汽车充电站设置分时电价进一步引导消费者消费,并使消费者形成良好的充放电习惯。云存储技术和智能电网相辅相成。云存储技术包含分布式存储和计算功能,能实时收集信息、传输信息,响应用户的需求。
国内对于电动汽车充放电价格的研究虽有不少,但大都还处在理论阶段,尤其是结合可再生能源的相关研究更为匮乏。国外对电动汽车充放电价格的研究更为多样化,且已将相关理论运用于实践,并取得了不错的效果。国内学者可结合国情以此为鉴,充分吸收并探索出更有意义的成果。文献[4]中虽然考虑了需求响应,并以此为依据制定了动态价格,但是未进一步考虑可再生能源的应用,研究供给侧的变化。文献[5]中为了满足电动汽车充电站的需求,考虑了价格信息和用户的充电习惯,拟定了充电价格策略,但并未考虑到放电价格的制定及引导策略,没有充分发挥电动汽车充放电的潜能。文献[6]在文献[5]的基础上进一步加入了V2G(vehicle−to−grid)模式,并考虑了配电侧风光互动,协调控制其运行,但在价格引导方面还尚有欠缺。在文献[7–11]中利用多种价格机制来控制一天中电动汽车在日常居住地的充电模式。然而,在商业或者工作地带,用户并不能对电动汽车的充电进行实时控制,需要设定一定的充电量和充电期限。文献[12–13]中提出了基于需求侧响应的价格优化算法,然而在实际情况下,需实时响应用户的充放电请求。文献[14]中提出了一种在线VCG(Virkrey−Clarke−Groves)模式,然而用户需支付的费用是在充电后才能确定,所以用户在充电前并不知道充电价格,因此该模式并不能起到很好的价格引导作用。文献[15–18]中提出了多种电动汽车在线有序充电算法。这些文献主要致力于有序引导策略的研究,并未考虑到为充电站和用户提供价格优化。
本文应用云存储技术,实时响应用户的充放电请求,提高客户的满意度。在目前已有的研究基础上,考虑到高比例可再生能源和电动汽车接入电网带来的问题,充分发挥电动汽车的存储功能,并有效利用充电站设施,提出新型价格模型。通过对电动汽车进行有序引导,缩小供求曲线的差距,保持供求曲线的稳定。对所提出的模型进行优化和数据分析,以期验证该模型的有效性。
1 电动汽车充放电对供求曲线的影响
1.1 电动汽车能量
借助云存储技术和智能电网,可实现智能电网和电动汽车用户之间的信息互动。在此考虑高比例可再生能源和大规模电动汽车接入电网对源−荷端的影响。
假设在一个地区范围内有n辆电动汽车,m个电动汽车充电站,充电站内有p个充电桩。为便于仿真模拟,假设电池种类、特性相同,且电动汽车充电站中每个充电桩均具有双向传输电能的功能。
在此研究一天中电动汽车充放电价格。将一天24 h平均分成24个时间段,每个时间段Δt=1h 。 Δt可以按需求设置为更小的值。充放电电动汽车集合为
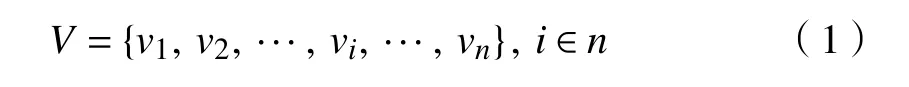
式中,v表示第i辆电动汽车。
电动汽车集合V包含两个部分:在t时刻只参与充电的电动汽车集合V,其数量为 n;只参与放电的电动汽车集合V, 其数量为n。因此有
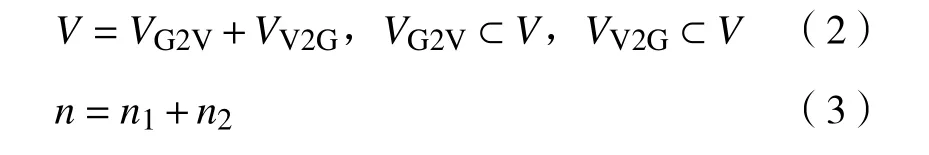
本文中考虑的是某个地区范围内的电动汽车充放电行为。这个地区所有的电能消耗由一个智能微电网(smart microgrid,SMG)提供。SMG基本能够满足所有电动汽车及生产、生活所需的电能。
在周期T中,电动汽车v充 放电量为 Q,有
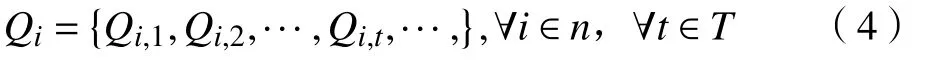
式中, Q为电动汽车 v在t时刻的交互电量。
电动汽车v在 t时刻的充电量表示为Q,其取决于t时刻的电池状态S和 充电目标量E。放电量表示为 Q,其取决于t时刻的电池状态S和 放电目标量 E,从而可以得到
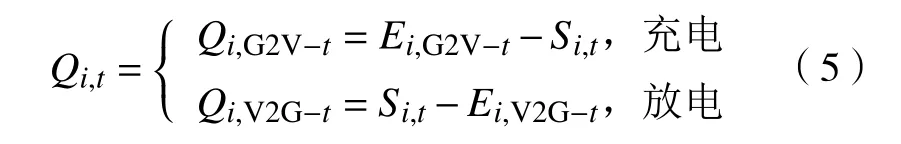
1.2 供求曲线
智能微电网采取常规能源和高比例可再生能源两种能源发电方式。微电网在t时刻供给量为 Q,需求量为 Q。为了表征供求曲线之间的差异,分别计算两者之间的差值 Q和比值Q,即
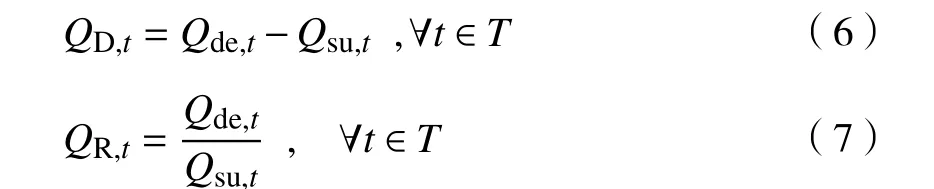
Q包括常规能源 Q、可再生能源Q和电动汽车放电量 Q的总和。另一方面,Q包括正常生产生活所需能量 Q和电动汽车充电量 Q的总和。因此有
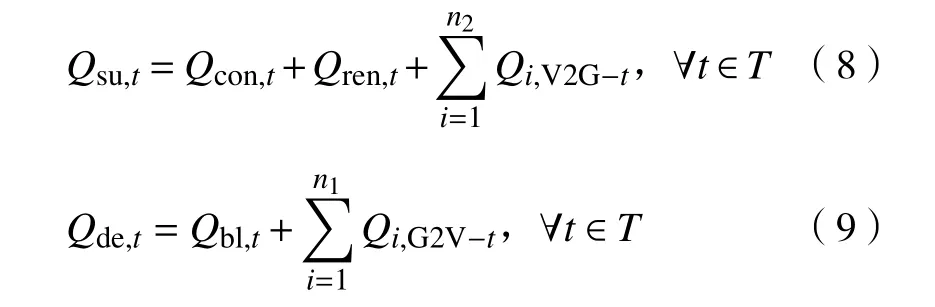
从式(6)~(9)中可得:可再生能源发电与电动汽车充放电直接影响供求曲线的稳定性,两者对供求曲线的稳定性可产生积极或消极影响。
2 分时充放电价格的制定
2.1 价格模型
云平台作为电动汽车和充电站之间沟通的桥梁,能够实时获得充电站的空闲情况并响应电动汽车的充放电请求。每辆电动汽车的相关信息V均存储在云端。
V包含用户姓名、用户密码、汽车序列号、电池类型、电池效率、电池状态和充电速度。根据充放电效率、充电速度和电池的电量状态等信息,可计算得到电动汽车的充放电时间。电动汽车在t时刻向云端发出充放电请求,包括充放电的时间范围和充放电的目标范围。然后经过云计算,将最合适的时间、价格发送给电动汽车,引导其充放电。
本文中考虑了两种价格优化模型:充电价格C和放电价格 C。基于预测的供求曲线,可以得到

式中:C为 从电网购电的成本;β为预先给定的常数。
从式(6)~(9)中可以进一步得到
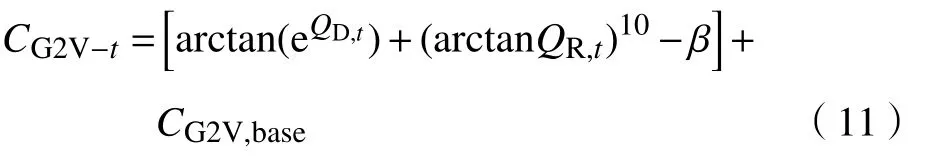
Q、 Q分别由式(6)、(7)给出。和式(10)类似,可以得到放电价格,即
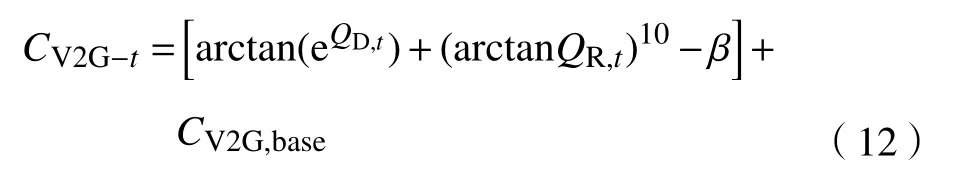
式中,C为向电网放电的基本费用。
从式(11)中可以得到:当需求量 Q不变或下降时,充电价格C随 着供给量 Q的增加而下降。相反,当供给量 Q不变或下降时,充电价格C随 着需求量 Q的增加而增加。
式(10)、(11)、(12)较精准地描述了电价特性,即电动汽车的充放电价格随着供求曲线的改变而实时变化。
2.2 优化价格模型
考虑到电动汽车充放电的影响,为了控制和维持供求曲线的稳定,需积极引导电动汽车有序充放电,减小 Q和 Q之间的供求差距。充电价格下降时引导更多的电动汽车充电,放电价格上升时引导更多的电动汽车放电。为了进一步通过价格引导来缓解充电站的空闲或忙碌问题,本文中在制定电动汽车充放电价格时考虑了充电站的空闲率。加入充电站的空闲率后的价格可表示为
当供求曲线稳定( Q 式中:j表示第j个充电桩;n、 n分别为充电站内用于充电、放电的充电桩个数; C、C分别为第j个充电桩的充电价格、放电价格。 目标函数为 约束条件为 式中:Q、 Q分别为电动汽车充电能量的最小值和最大值;Q、 Q分别为电动汽车放电能量的最小值和最大值;E、 E分别为充电目标量的最小值和最大值;分别为放电目标量的最小值和最大值;C、 C分别为充电价格的最小值和最大值;S为电池的荷电状态。 为了使模型求解简便,假设电动汽车在快充情形下充放电,充放电功率在各个时刻保持不变。考虑到可再生能源发电的随机性和短时间内可调度的电动汽车充放电容量的有限性,假设发电量和需求量之间的差异不会特别显著,使得可调度电动汽车的充放电容量满足供求稳定。 当供求曲线不稳定( Q>Q)时,有 目标函数为 约束条件为 无论是以上哪种情形,都需要解决双目标问题,变量为电动汽车的充放电量。因此,采用线性加权法将双目标函数转化为单目标函数。 式中: s、 s均 为权重系数,且 s+s=1; f、f分别为 f、 f的最小值。 为了使用户的利益和充电站的效益公平化、均衡化,在此取 s=s=0.5。在某些情况下,如果想提高某一方的利益,可适当提高其权重系数。对于线性优化模型求解,本文采用粒子群优化算法。 在此考虑两种场景,以便进行分析、比较,以验证所提出的模型是否能达到预期设想。第一种是常规模式,即只采用以上的定价方式,并不对其进行线性优化。第二种是采用所提出的优化价格模型。为了优化充放电价格并使供求曲线保持稳定,电动汽车用户、充电站、智能电网需实时保持通信来响应电动汽车的充放电请求。表1、2分别为算例中采用的相关仿真参数和电动汽车参数。 表1 仿真参数 电动汽车/辆充电站数量/个充电站中充电桩数量/个充电汽车数量与充电桩数量比值/%放电汽车数量与放电桩数量比值/%充电目标量/(kW·h)放电目标量/(kW·h)2 000 20 2 000 70 30 30~60 10~30
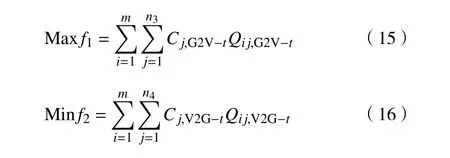
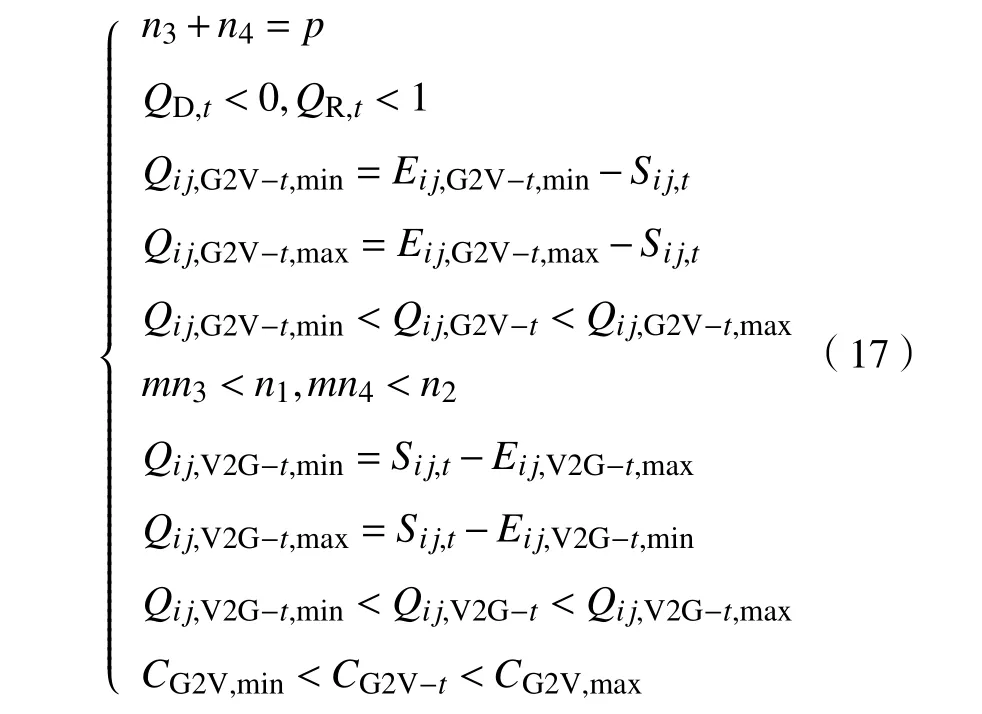
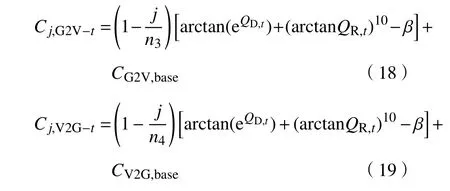
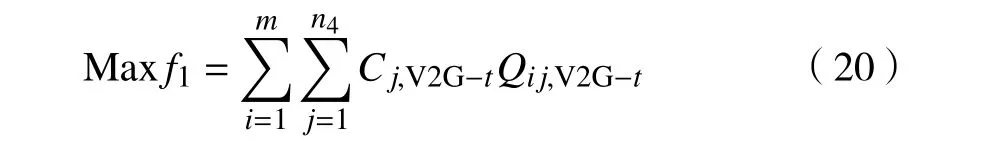
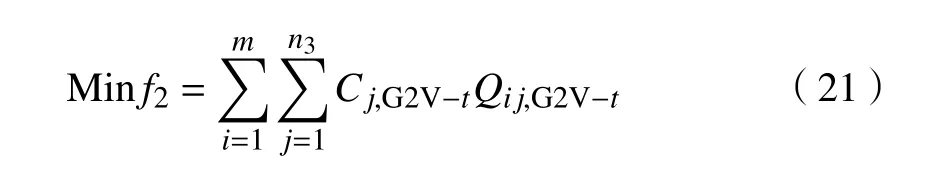
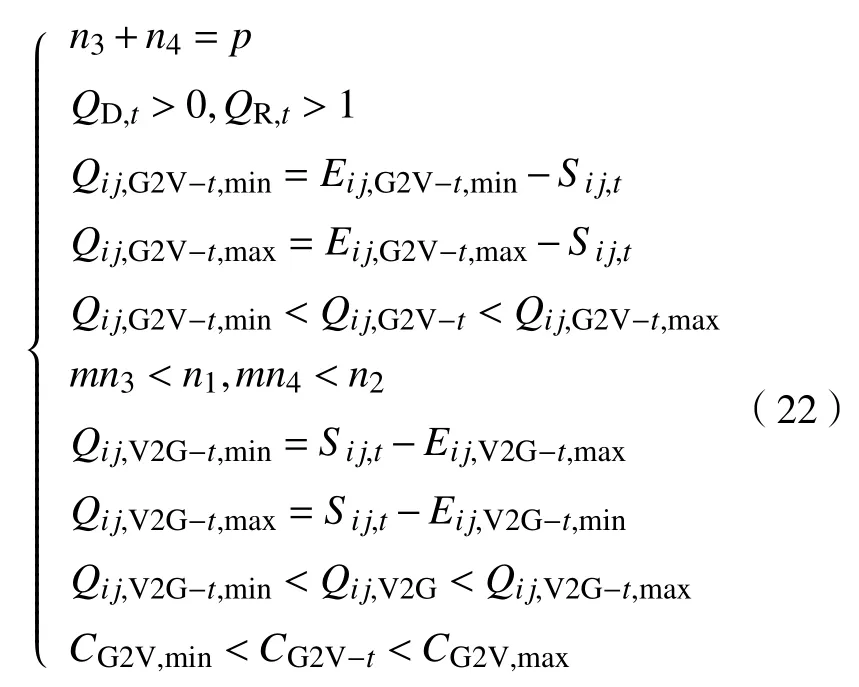
2.3 模型求解
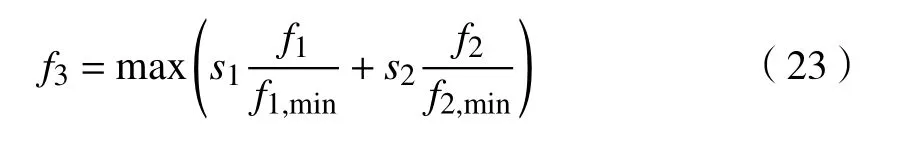
3 算例分析
3.1 参数设置
Tab.1 Simulation parameters
表2 电动汽车参数
Tab.2 Parameters of the electric vehicles (EVS)
电池储能容量/(kW·h)额定充放电功率P/kW充放电效率/%60 9.6 90.85
3.2 仿真分析
图1为电动汽车一天中各个时刻充放电量。从图中可以看到,一天中有两个高峰时期:早高峰(6:00~8:00)和晚高峰(17:00~20:00)。在高峰时期,电动汽车的数量取最大值2 000。图2为每辆电动汽车电池初始电量。为了使仿真结果更加真实、有效,在两种场景中均假设充电汽车数量大于放电汽车数量。
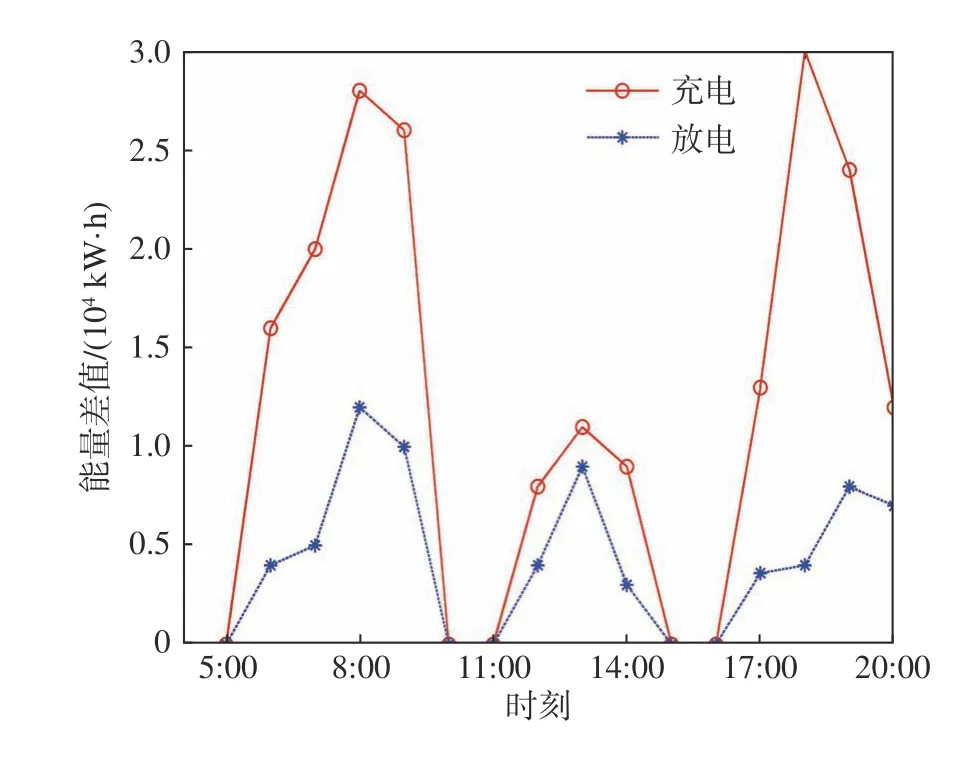
图1 电动汽车一天中各个时刻充放电量Fig.1 Charging and discharging energy of EVS in one day
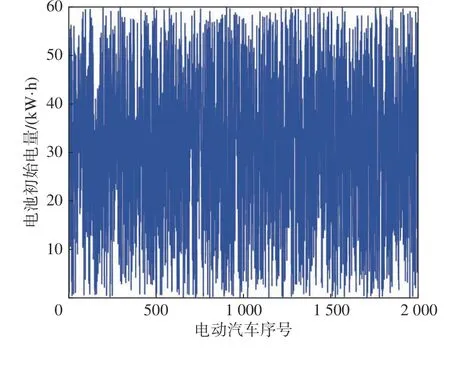
图2 电动汽车电池初始电量Fig.2 Initial energy of EVS battery
假设供求曲线不稳定,例如供小于求,且电动汽车充放电随机接入。图3为常规模式下一天中充放电量差值。从图中可以看到,在负荷高峰时期,能量供求差值显著增加。在常规模式下某充电桩的电动汽车动态充放电价格如图4所示。由图中可以看出,供求曲线不稳定时,充电价格较高,尤其是在高峰时期。
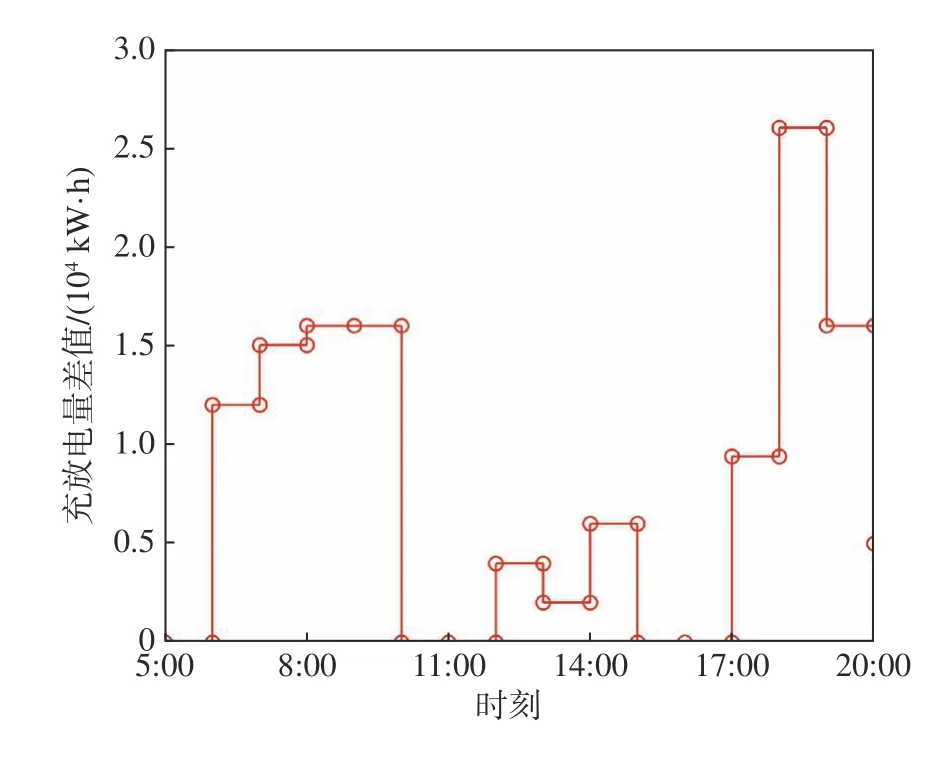
图3 一天中电动汽车充放电量差值Fig.3 Energy difference between charging and discharging of EVS in one day
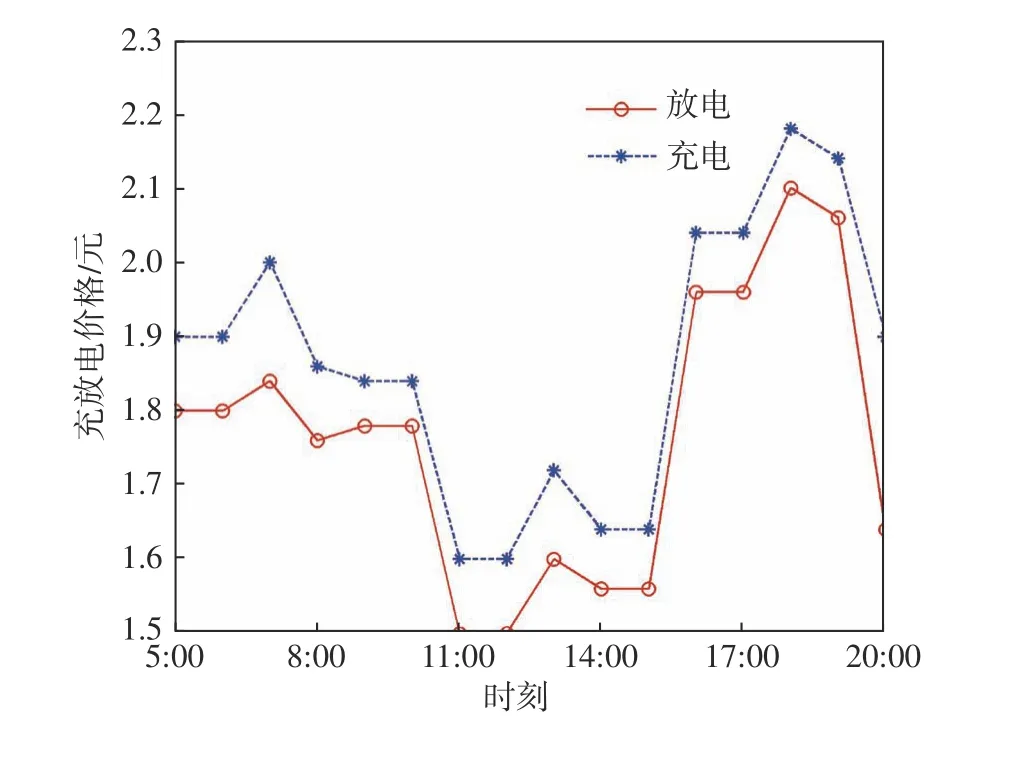
图4 常规模式下电动汽车动态充放电价格Fig.4 Electricity price of EVS charging and discharging in the normal mode
能量比值 Q与充电价格的关系如图5所示。当供等于求时,能量比值为1,此时电价固定。随着能量比值的增大,电价增长。由图5中可以看出,可用价格信息来代替供求信息。
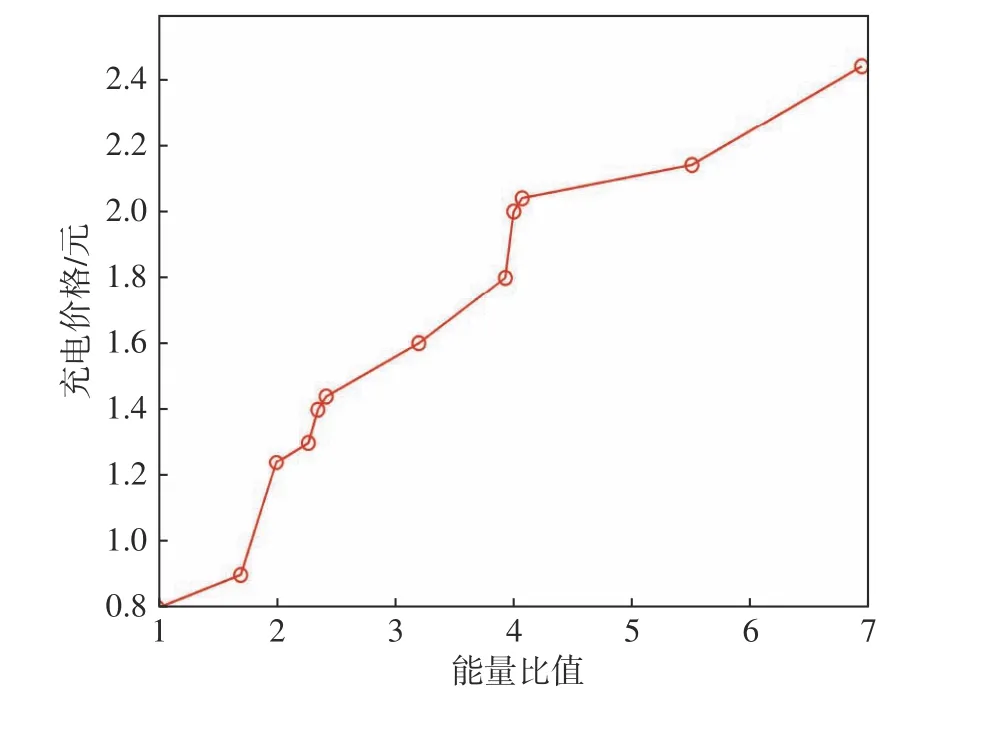
图5 能量比值与充电价格的关系Fig.5 Relationship between the energy ratio and charging price
常规模式下和采用优化价格模型优化后电动汽车放电价格的对比如图6所示。从图中可以看到:早高峰时期,放电价格从1.24~1.78元上升到1.80~1.90元;晚高峰时期,放电价格从0.76~0.84元上升到1.90~2.12元。充电价格的下降在供小于求的情形下具有重要意义,表明供求曲线趋于稳定。
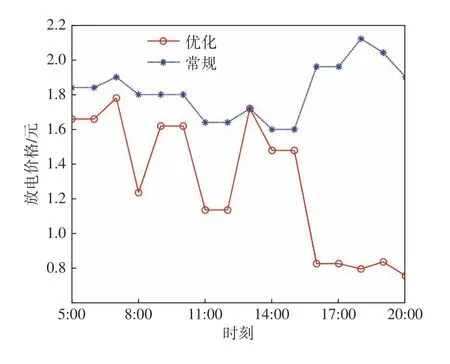
图6 常规模式下和优化后的放电价格对比Fig.6 Comparison of discharging price between the normal mode and the optimization one
在常规模式下电动汽车无序充放电,导致供求曲线差异更大。经价格优化后充电价格下降,有序充电使供求曲线相对稳定。常规模式下和优化后的能量比值和能量差值如图7所示。从图7(a)中可以看到,在18:00,常规模式下能量比值达到最大值7.00,优化后下降到2.32。与常规模式下相比,图7(b)中优化后供求能量差值的初始值为负值,此时供求关系变得稳定。从图7中可以得出,本文所提出的优化价格模型能够有效地稳定供求曲线。
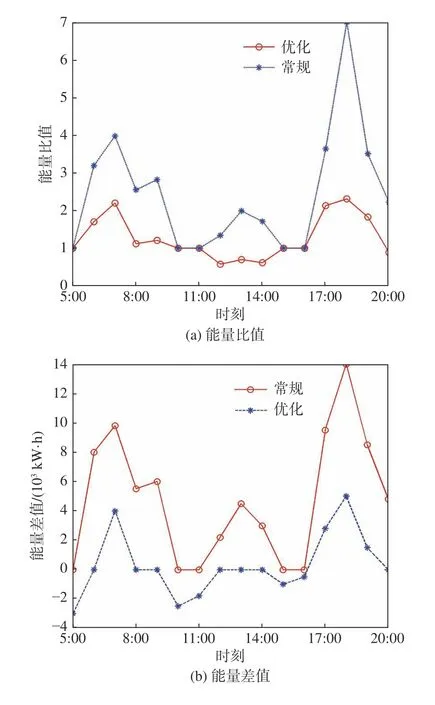
图7 常规模式下和优化后的供求能量比值、能量差值Fig.7 Energy ratio and energy difference based on supply and demand curve in the normal mode and after the optimization
两种场景下电动汽车在各个时刻充电量对比如图8所示。从图中可以得到:与常规模式相比,优化后电动汽车的充电量有所下降,尤其是在高峰时期,8:00时充电量从14 500 kW·h下降到7 000 kW·h,18:00时充电量从15 000 kW·h下降到8 000 kW·h。对于风电功率的消纳效果虽不是很明显,但与常规模式下相比,优化后电动汽车充电站从电网购电量大大减少,减少了电动汽车充电站的运营成本。
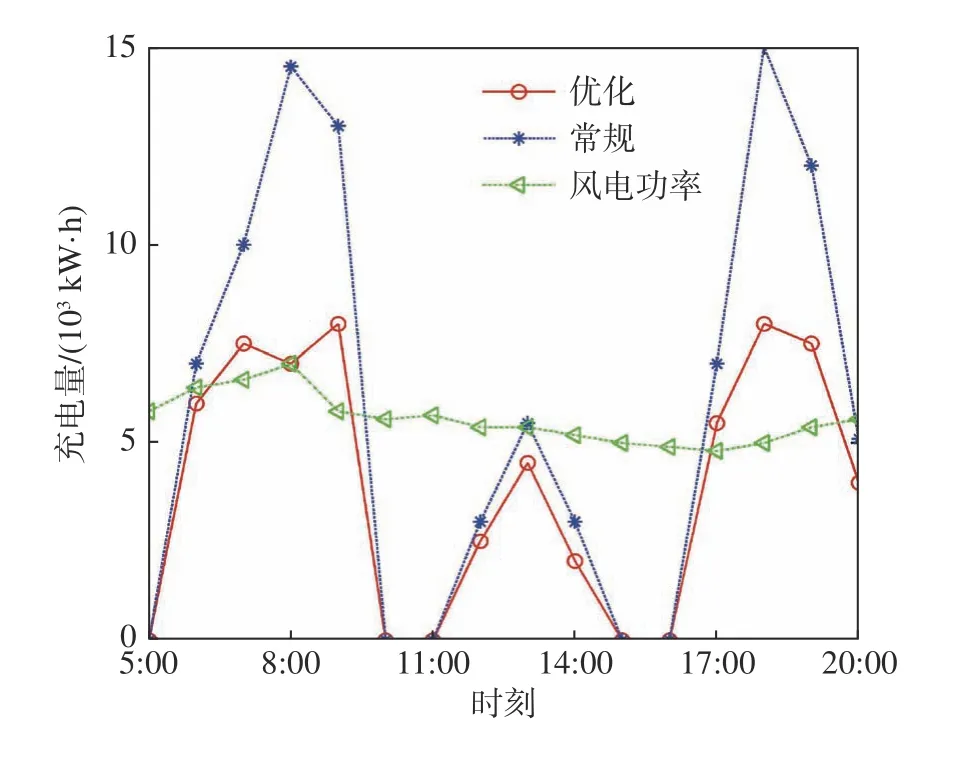
图8 常规模式下和优化后的充电量对比Fig.8 Comparison of charging energy between the normal mode and the optimization one
常规模式下和优化后晚高峰时期供求变化如图9所示。从图中可以得到,与常规模式下相比,优化后供求曲线相对稳定。由此可以看出,实施优化价格模型后,供求曲线得到了较大的改善,从而验证了该模型的有效性和合理性。
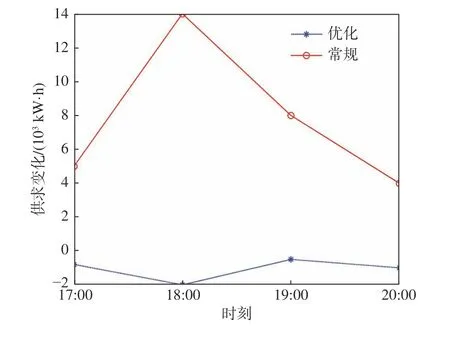
图9 常规模式下和优化后晚高峰时期供求变化Fig.9 Supply-demand changes in the evening rush hour between the normal mode and the optimization one
4 结 论
本文提出了电动汽车的充放电价格模型,以期引导电动汽车在智能电网中有序充放电。根据供求曲线实时响应电动汽车用户充放电请求。将电动汽车充放电价格模型归结为多目标线性规划问题,利用粒子群算法求解,达到维持供求曲线稳定的效果,并在高峰时期有序安排电动汽车充放电以平衡供求两者之间的关系。当充放电价格满足智能电网和电动汽车用户的成本要求时,利用分时电价响应用户充放电请求。仿真结果表明,基于智能电网技术可实现实时响应充放电需求,能有效减少供求曲线的差值,保持供求曲线的稳定性。
