关注微专题复习 促进学生深度学习
2021-07-19黄志平
黄志平


摘 要:深度学习是一种批判性的、高质量的、理解性的学习方式,能有效促进学生思维水平的发展.在各章节阶段复习和初三总复习中可充分利用数学微专题“准、细、深”等特点,设计形式多样的微专题.现以设计“2019年福建中考第24题微专题复习”为例,谈谈如何设计微专题,进行精准、简约的教学,促使学生能把一类问题想深、想透,形成自己的批判性思维和个性思维,达到实现深度学习的目标.
关键词:复习;微专题;深度学习
初中阶段深度学习的根本目的是促进学生思维水平的发展,指在老师创设的自由探索的空间,围绕某个学习主题展开自主探究、合作交流、展示质疑等活动,是一种主动的、批判性的、创造性的学习方式.通过深度学习,学生能深刻理解数学知识,领悟数学本质,获取知识背后蕴藏的丰富思维价值.作为数学教师,深度教学不是指单纯把知识教深、教难,而是指对教材钻研深透,能有效引导学生把主要精力放在知识重难点上,促进学生理解学科本质,领悟数学思想.作为学生,深度学习是种“理解性”学习,是一种能真正启动思维,让自己在学习中进行深度思考,理解每个知识的来龙去脉的学习方式.通过把自己的学习感悟有机融入到原有的认知结构中,从而达到提高思维能力,提升思维品质和发展高阶思维的目标.
为了促进学生深度学习,在各章节阶段复习和初三总复习中有必要对学过的知识重新建构、重新融合、重新完善,给学生创造深度学习的时间和空间,为实现学习能力再提升创造契机.而数学微专题复习具有“因微而准、因微而细、因微而深”等特点,能起到“以小见大”,促进学生对知识理解深刻、感悟透彻.因此,数学微专题复习是促进学生深度学生的有效途径.在初三总复习中,各种形式的测试贯穿于一轮、二轮教学中.教师如果能设计基于试卷讲评拓展的微专题复习,不仅能帮助学生探求错因、查找缺漏、彻底纠错,而且能帮助学生提高思维水平,实现深度学习.
1 2019年福建中考第24题微专题复习概述
在初三复习期间选取了2019年福建中考第24题给学生做作业: 如图1,四边形ABCD内接于☉O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF,CF.
(1)求证:∠BAC=2∠CAD;
(2)若AF=10,BC=4,求tan∠BAD的值.
思路突破:(1)根据圆周角性质和已知条件AC⊥BD得到∠CAD=∠CBD=90°-∠ACB,再根据等腰三角形性质得到∠ABC=∠ACB,所以∠BAC =180°-2∠ACB=2(90°-∠ACB),即∠BAC=2∠CAD;
(2)易证得∠CFB=∠CBF=∠BAC,由等腰三角形的判定可得BC=CF=4,即可证得AC垂直平分BF,所以AB=AF=10.分别在RtΔAEB和RtΔBEC中,利用勾股定理BE2=AB2-AE2=BC2-CE2求得AE=6,CE=4,BE=8,再利用ΔADE∽ΔBCE可得DE=3,AD=3.接着过点D作DH⊥AB于点H,然后根据ΔABD面积公式求得DH=,进而求得AH=,最后利用锐角三角函数定义求解tan∠BAD.
此题主要考查圆的有关性质、锐角三角函数和等腰三角形的判定与性质等基础知识;考查了几何直观、运算能力与推理能力;考查了函数与方程思想、化归与转化思想,学生的答题错误率很高.笔者进行了思考,发现学生对圆的有关性质和三角函数的求解掌握不够扎实,特设计了一节“三角函数与圆微专题”复习课.本微专题通过“以退为进,以小见大,以学生的最近发展区”巧妙设置微专题.最大限度降低学习难度,深度挖掘学生学习中可能遇到的问题,以问代教,让学生的认知逐步深入,进行深度学习,达到发展学生核心素养的目标.
2 教学过程设计
环节一 课前练习,奠定基础
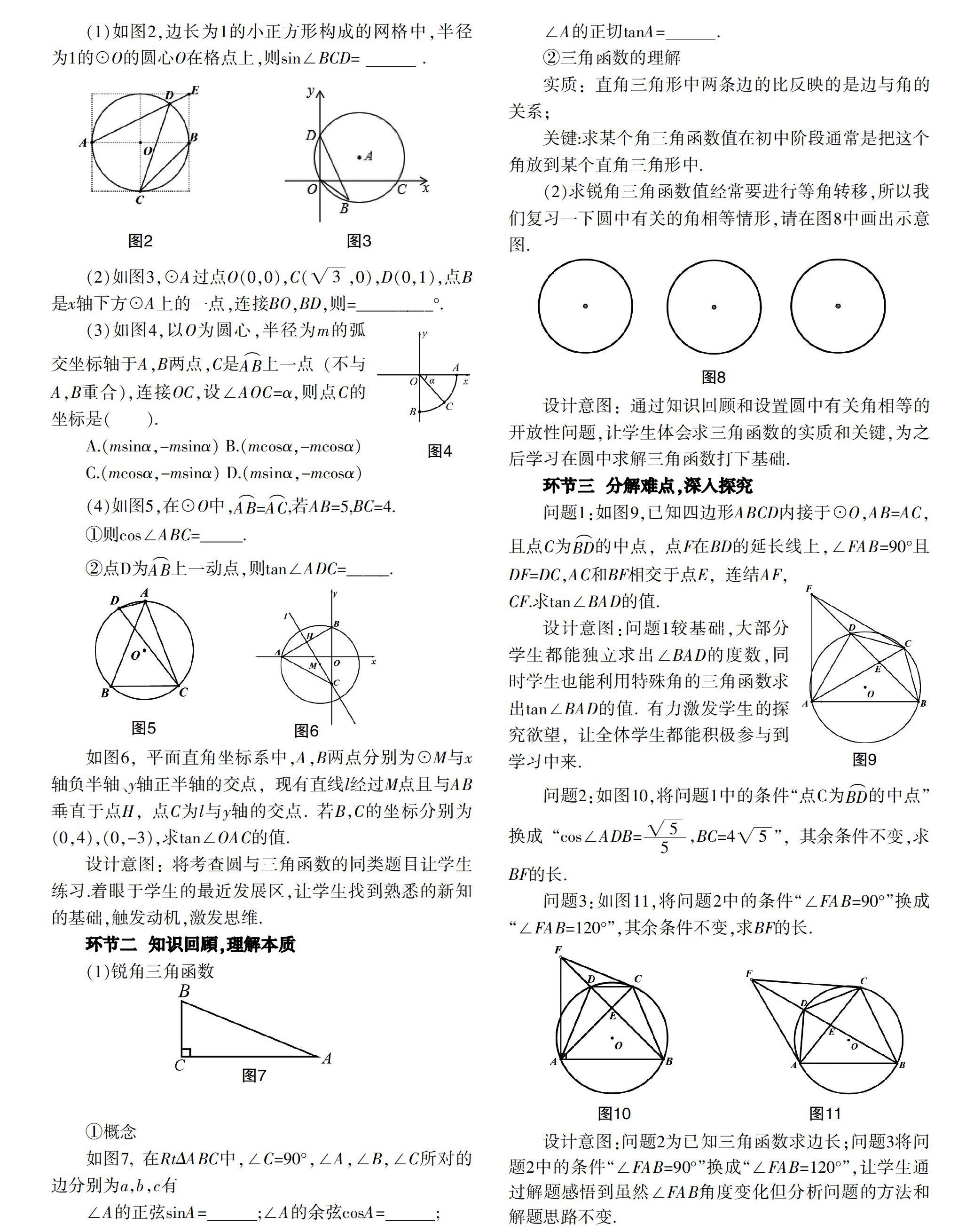
(1)如图2,边长为1的小正方形构成的网格中,半径为1的☉O的圆心O在格点上,则sin∠BCD= .
(2)如图3,☉A过点O(0,0),C(,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则=_________°.
(3)如图4,以O为圆心,半径为m的弧交坐标轴于A,B两点,C是[⌒][AB]上一点(不与A,B重合),连接OC,設∠AOC=α,则点C的坐标是().
A.(msinα,-msinα) B.(mcosα,-mcosα)
C.(mcosα,-msinα) D.(msinα,-mcosα)
(4)如图5,在☉O中,[⌒][AB=AC][⌒],若AB=5,BC=4.
①则cos∠ABC=_____.
②点D为[⌒][AB]上一动点,则tan∠ADC=_____.
如图6,平面直角坐标系中,A,B两点分别为☉M与x轴负半轴、y轴正半轴的交点,现有直线l经过M点且与AB垂直于点H,点C为l与y轴的交点.若B,C的坐标分别为(0,4),(0,-3),求tan∠OAC的值.
设计意图:将考查圆与三角函数的同类题目让学生练习.着眼于学生的最近发展区,让学生找到熟悉的新知的基础,触发动机,激发思维.
环节二 知识回頋,理解本质
(1)锐角三角函数
①概念
如图7,在RtΔABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c有
∠A的正弦sinA= ;∠A的余弦cosA= ;
∠A的正切tanA= .
②三角函数的理解
实质:直角三角形中两条边的比反映的是边与角的关系;
关键:求某个角三角函数值在初中阶段通常是把这个角放到某个直角三角形中.
(2)求锐角三角函数值经常要进行等角转移,所以我们复习一下圆中有关的角相等情形,请在图8中画出示意图.
设计意图:通过知识回顾和设置圆中有关角相等的开放性问题,让学生体会求三角函数的实质和关键,为之后学习在圆中求解三角函数打下基础.
环节三 分解难点,深入探究
问题1:如图9,已知四边形ABCD内接于☉O,AB=AC,且点C为[⌒][BD]的中点,点F在BD的延长线上,∠FAB=90°且DF=DC,AC和BF相交于点E,连结AF,CF.求tan∠BAD的值.
设计意图:问题1较基础,大部分学生都能独立求出∠BAD的度数,同时学生也能利用特殊角的三角函数求出tan∠BAD的值.有力激发学生的探究欲望,让全体学生都能积极参与到学习中来.
问题2:如图10,将问题1中的条件“点C为[⌒][BD]的中点”换成“cos∠ADB=,BC=4”,其余条件不变,求BF的长.
问题3:如图11,将问题2中的条件“∠FAB=90°”换成“∠FAB=120°”,其余条件不变,求BF的长.
设计意图:问题2为已知三角函数求边长;问题3将问题2中的条件“∠FAB=90°”换成“∠FAB=120°”,让学生通过解题感悟到虽然∠FAB角度变化但分析问题的方法和解题思路不变.
环节四 数学运用,链接中考
问题4:如图12,四边形ABCD内接于☉O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连结AF,CF.若AF=10,BC=4,求tan∠BAD的值.(2019年福建中考第24题有删减)
问题5:如图13,将问题4中的条件“若AF=10,BC=4”删去,其余条件不变,请判断直线CF是否与☉O相切?若相切,请说明理由.
设计意图:问题4为2019年福建中考第24题第(2)步,可看作把问题2中的条件“∠FAB=90°”转变成“AC⊥BD”然后利用已知条件求∠BAD的正切值.问题5通过深度挖掘本试题隐藏的结论设置开放性问题,让学生先判断直线与圆的位置关系再进行证明,有效发展学生思维能力.通过让学生观察、操作、猜想、验证等活动促进学生进行深度思考,发展高阶思维.
环节五 拓展应用,升华思维
拓展提高1:如图14,将问题4中的条件“若AF=10,BC=4”换成“∠CAB=30°, AF=10,点M是AB上动点”,其余条件不变.求CM+AM的最小值.
拓展提高2:如图15,将拓展提高1中的条件“∠CAB=30°”换成“∠CAB=15°”,其余条件不变.求CM+AM的最小值.
拓展提高3:如图16,四边形ABCD内接于☉O,AB= AC,点F在BD的延长线上,∠FAB=90°且DF=DC,AC和BF相交于点E,连结AF. 若cos∠ADB=,BC=4.现将线段BC绕着点B按逆时针旋转到BC',旋转角为α(0°<α<∠ABC),连结FC',AC'.求FC+AC'的最小值.
设计意图:拓展提高1 是改变2019中考24题条件,让学生在探究“线段CM+AM”最小值问题过程中,不断提升解形如“线段a+kb(其中0 环节六 自我评价,反思内化 分享复习的乐趣,通过今天的复习,你学习了哪些知识?掌握了哪些方法?积累了哪些经验? 设计意图:让学生分别从知识、方法和学习经验进行反思、总结,从而把所学的感悟和体验内化为自己的知识结构,逐渐形成良好的数学思维品质与关键能力. 3 教学思考 在各阶段教学中,可设置微专题复习来改变复习中出现的“知识简单回顾”“重复强化训练”和“专题复习入口大”等效率低下的复习状况.在微专题复习的学习中,让学生真正深入到问题的探究中,在掌握和熟练运用知识的同时,深刻理解学科本质,提升解决问题的能力,是促进学生深度学习的的一条有效途径. 3.1 微专题复习要聚焦核心知识,促进学生深度感悟 微专题复习具有“目标准、小见大、专见强”等特点,能让教师从教学的核心知识和知识系统考虑设置微专题.只有聚焦数学核心知识,准确把握学科教学关键点,教学中才能紧紧围绕教学目标开展精准的教学.只有有效突破教学重难点,扬长避短,才能提高学生思维能力,发展高阶思维,从而让学生实现有深度的学习.在平时教学中教师要关注每个年级、每个章节和每节课的主体内容和学科本质.在初三总复习时,可针对性突破重点、关键点、疑点、易错点和混淆点开展微专题复习.其中重点和关键点可从数学模型、重要方法和典型题型方面进行建构;疑点、易错点和混淆点可从即时困惑和常见错误等方面建构.通过微专题复习,能让学生对核心知识进行思路探索,优化解题方案,修正解题过程.通过教师的引领,学生对解题过程进行提炼、反思、提出独创性的见解,进行高质量学习,从而促进学生对核心知识的内化和感悟. 3.2 微专题复习要关注学习过程,帮助学生深度参与 微专题复习具有“切口小、主题强、角度新”等特点,能为学生学习提供很好的学习资源.在进行微专题设计时要关注知识的形成过程,让学生在学习过程中亲身經历完整的学习过程“情境—问题—假设—推理—验证—运用—反思”,让学生在深度参与中实现知识与能力的双提高.在本案例中能设置低起点、缓梯度的试题,为全体学生创设独立思考、自主探索、合作交流和展示讲解等活动,让学生都能深度参与到学习中来.在课堂学习中,学生不断积累解决各种问题的活动经验,在解决问题中不断体验到成功的愉悦,在提升思维品质的同时也锻炼了自己的意志.让学生在微专题的学习过程中形成自己独特的必备品格与关键能力,有效提升核心素养. 3.3 微专题复习要设计探究问题,引导学生深度思考 微专题复习具有“深刻性、系统性、拓展性”等特点,能为学生提供探究问题的空间.一方面,深度学习是学生的自我求知欲望强烈,对所学习内容进行准确的、深刻的学习,是提升学生思维水平的重要途径.另一方面,深度学习能有效促进学生进行深度思考,进行批判性学习,通过微专题复习将学习体会、感悟和经验内化为自己的思维体验,有效提高学生思维能力,达到发展学生核心素养的目标.基于微专题的作用,教师要深入挖掘教学素材,围绕主题设计探究问题,力求入木三分.在本案例中,选择省内中考试题,进行多维解析,设计易错点、难点微专题,引导学生深度思考.在设计问题时要考虑“退”的原则,退到问题的最原始状态设计探究性问题进行变式教学,然后逐步拓展延伸到原题、问题的核心.这样可以把一个个知识点串“珠”成“链”,让学生在各个问题的不断探索中获得学习能力,在知识的拓展中不断提升思维能力,达到发展学生高阶思维的目标. 深度学习是一种主体性、深刻性、高质量的学习,是一种直指学科本质、理解性和批判性的学习.而微专题复习话题集中、针对性强,具有“微”和“专”等特点,适用于各个阶段的复习.教师可根据各阶段的教学目标,精心设置微专题复习.通过创设灵动的课堂,唤醒学生的求知欲望,让他们经历知识的发现与建构过程,达到“会一题,得一法,懂一片”,促进学生对知识理解深刻、感悟透彻,达到深度学习的目标.
