基于岩体劣化顺层灰岩岸坡滑移-弯曲失稳机理和评价*

2021-07-19闫国强黄波林代贞伟

工程地质学报 2021年3期

闫国强黄波林王勋代贞伟张鹏秦臻

(①中国地质大学(武汉)工程学院，武汉 430074，中国)(②防灾减灾湖北省重点实验室，三峡大学，宜昌 443002，中国)(③重庆市地质矿产勘查开发局107地质队，重庆 401120，中国)(④中国地质调查局武汉地质调查中心，武汉 430205，中国)

0 引言

由于三峡工程冬蓄夏洪的水位调控，形成了高程145～175m之间的水位劣化带。在库水位升、降循环中，变幅带岩体处于一种水力化学反复交替状态，这种多场耦合作用对岸坡坡脚来说是一种“劣化损伤”作用(Hale， 2003)，促使劣化带岸坡坡脚处岩体力学参数趋弱、层间分离(Ford et al.，2007；黄波林等， 2019；殷跃平等， 2020)，这进一步加速了岸坡变形破坏演化与岩体劣化进程(张倬元等， 2009)。在三峡库区巫峡段广泛分布有“中倾-陡倾”顺层灰岩岸坡(余姝等， 2019)，顺层岸坡本身作为极易诱发大型致命滑坡的结构类型(殷跃平， 2005； Hungr et al.，2014)，叠加岸坡坡脚的持续劣化、软化效应，极易发生“滑移-弯曲”失稳破坏(刘云鹏， 2017；黄波林等， 2020)，对三峡库区黄金水道航运及当地人民生命财产构成极大威胁。

库区顺层岩质岸坡失稳规模巨大，滑移变形速度往往较快，其变形失稳主控区为坡脚阻滑段及岩层面(冯君， 2002；殷跃平， 2005)。顺层岸坡最典型的两种破坏模式为：滑移-拉裂与滑移-弯曲(张倬元等， 2009)。特别是“滑移-弯曲”模式形成机制较为复杂，破坏具有隐蔽性和突发性，对顺层岩质岸坡“滑移-弯曲”失稳研究具有重要意义(汤明高等， 2016)。1963年10月9日震惊世界的瓦伊昂滑坡即为典型的顺层“滑移-弯曲”破坏，方量高达2.6×108m3，滑速为20～30m·s-1(Müller， 1987a；肖诗荣等， 2010)。不少学者(Moregenstern， 1963； Voight et al.，1992； Semenza et al.，2000; Sitar et al.，2005; Paronuzzi et al.，2013)对瓦伊昂滑坡的启动及快速滑移机制作出努力探索，其中前缘坡脚阻滑段以及滑移面受库水作用软化、力学参数急剧衰减导致岸坡溃屈失稳并快速滑移成为多数学者共识(Hendron et al.，1985； Müller， 1987b； Rinaldo et al.，2005)。我国同样不乏滑移-弯曲岩质岸坡破坏实例，且多演化为大型滑坡，如雅砻江二滩水电站霸王山古滑坡(张倬元等， 2009)、雅砻江锦屏一级水电站近坝库岸边坡、三峡库区木鱼包滑坡(邓茂林等， 2019)、黄河李家峡水电站坝前2#边坡(聂德新等， 1997)等；对“滑移-弯曲”类滑坡不少学者推导过解析解并进行物理模型试验验证：如孙广忠等(2011)基于压杆稳定理论推导得临界坡长；李树森等(1995)基于多层板梁理论求得临界挠曲段近似解；刘钧(1997)将顺层岸坡视为简支梁并采用能量法得到临界挠曲段平衡方程；刘小丽等(2002)、冯君等(2010)采用四边简支弹塑性板模型，根据能量法推导出临界挠曲段高阶平衡方程；蒋良潍等(2006)采用等厚弹性板梁模型，从理论上求解出挠曲线的适定三阶微分方程；汤明高等(2016)采用物理模型、数值模拟和理论计算相结合的方法，提出了顺层斜坡产生滑移-弯曲变形的地质力学条件、临溃状态判别与早期识别标志； Lo et al.，(2017)采用物理模型研究顺层滑坡发生滑移-溃屈的前提条件和变形失稳特征。

综上所述，无论是基于压杆(梁)稳定理论(李树森等， 1995；刘钧， 1997；蒋良潍等， 2006；孙广忠等， 2011；汤明高等， 2016)或者是弹塑性板模型(冯君， 2005；刘小丽等， 2002；冯君等， 2010)推导出的临界挠曲段与临界应力，其稳定性评价较少考虑岸坡坡脚处的劣化损伤特性，在边界条件不变的情况下，计算出的稳定状态不变，这与巫峡段顺层灰岩岸坡动态劣化实际不符(黄波林等， 2019， 2020)。随着库水周期性水力化学作用，即使是相同的边界约束，由于岸坡坡脚抗弯刚度等力学指标的衰减劣化，岸坡整体稳定性较之前呈快速下降趋势(闫国强等， 2020)。因此对于岩体劣化特征明显的巫峡段顺层灰岩岸坡“滑移-弯曲”评价，亟待引入一种考虑岩体劣化效应的顺层岸坡概化模型及计算方法。本文结合巫峡青石段顺层灰岩岸坡劣化特征，建立考虑坡脚劣化效应的顺层“滑移-弯曲”力学模型。根据弹塑性受压板理论，引入岩体GSI(t)劣化函数(殷跃平等， 2020)，利用能量法推导出临界挠曲段高阶平衡方程。与现有若干方法相比，本文推导方法可对受损伤劣化的顺层滑移-弯曲岸坡进行评估，具有更广泛的应用性和适用性，最后针对该类型的岸坡结构提出了相应的防治建议。

1 巫峡段顺层岸坡宏观劣化破坏特征

2008～2020年间对三峡库区巫峡段岩溶岸坡进行了长期跟踪调查。调查区两岸总长为43.5km，其中顺层岸坡总长为20.68km，占比48%。最初岸坡岩体劣化宏观现象在龚家坊附近(龚家坊—独龙一带)发现(马昊等， 2020)，尔后多样化的岩体劣化现象在许多岩溶岸坡中被发现。特别是青石村—抱龙河口段两岸顺层灰岩岸坡劣化现象极为显著(黄波林等， 2019， 2020；闫国强等， 2020)，此处两岸劣化带顺层岸坡长达9.29km，占巫峡顺层岸坡总长45%，且岩层倾角大部分处于40°～45°及以上，属于典型的“中倾-陡倾”顺层岸坡，极易产生顺层“滑移-弯曲”失稳(图1、图2)。

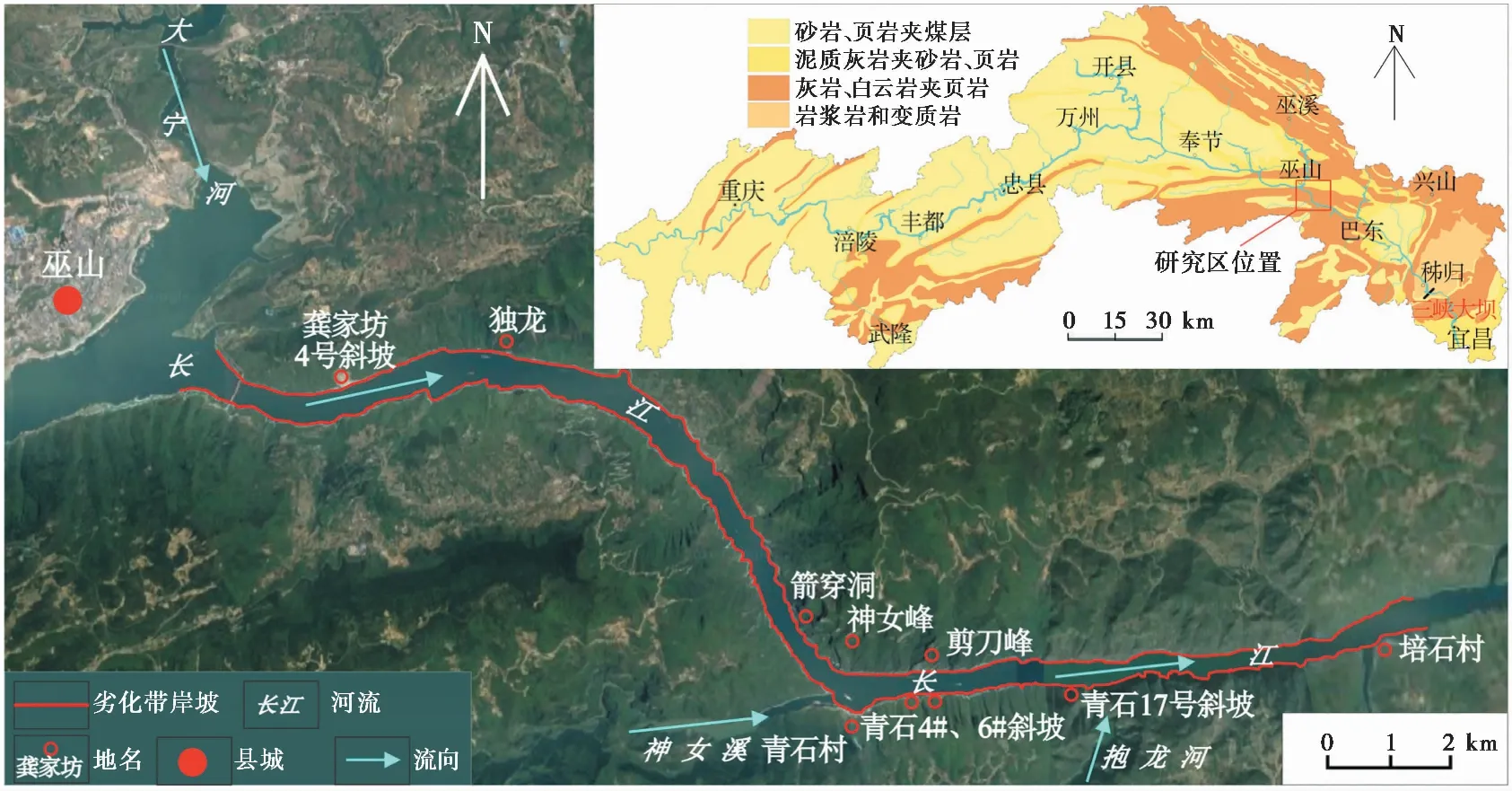
图1 三峡库区岩性分布图及巫峡段岩体劣化重点调查区图

图2 青石村—抱龙河口段顺层灰岩岸坡“滑移-弯曲”劣化破坏现象

岸坡岩体在长时间物理化学作用下，岩体强度逐渐劣化，会促使已有节理裂隙进一步加宽变深，岩层面趋于分离(黄波林等， 2019；闫国强等， 2020；殷跃平等， 2020)。青石村至抱龙河口段右岸顺层斜坡由于30m劣化带长期的水岩劣化作用，导致岸坡“趾部”一定程度的软化，岩层面趋于脱空，在后部上覆山体压力作用下，形成了大范围的“滑移-弯曲”挠曲带(图2a)。挠曲带处岩体应力集中，叠加物理化学劣化作用极易破碎，往往是“滑移-弯曲”类岸坡的潜在“剪出口”。“滑移-弯曲”类岸坡后部岩体可以简化为一个主动传力区，前缘挠曲段可视为被动挤压挠曲带(图2b)。根据前期调查研究(黄波林等， 2019， 2020；殷跃平等， 2020)，岩体劣化主要沿坡脚岩体与岩层结构面进行，前缘坡脚阻滑段受劣化损伤趋于“软化”，岩体抗弯刚度减小。这加剧了岸坡前缘挠曲段变形，同时由于岩体结构面的进一步碎裂、劣化，促进了坡脚劣化带处潜在“剪出口”日趋贯通，最终将导致岸坡整体滑移-弯曲、溃屈失稳。

2 考虑岩体劣化效应的计算模型

2.1 地质模型建立

一般而言，滑移-弯曲失稳型顺层边坡岩板的挠度要远小于其厚度(图2b)，同时顺层岩板弯曲时引起的弯曲应力比板的中曲面应力大。因岩板抗拉能力较弱，岩板在弹塑性翘曲时，其应力、应变部分超过材料的弹性阶段而进入塑性范围，故可取弹塑性薄板小挠度理论进行计算(冯君等， 2010)。

根据上述假设，建立地质力学模型如图3。设顺层岩板沿x轴向总长AC为L，y轴向长b，弯曲段AB长为lcr，则滑移段BC长为L-lcr，岩板等厚为h，建立坐标系如图3所示。根据相关研究将A端简化为铰支座，B端简化为辊轴支座是偏安全的(刘钧， 1997)。对于多层板可假定各层挠曲线函数相同且均质等厚(李树森等， 1995)，这样顺层岩质边坡的稳定问题可简化为四边简支薄板的翘曲模型。对四边简支的矩形薄板， 4个支点处的挠度与弯矩等于0，则有边界条件为：

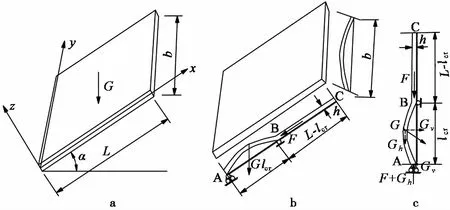
图3 “滑移-弯曲”边坡地质力学模型

(1)

纳维把挠度ω表示为如下的双重三角级数(徐芝纶， 2002)：

(2)

式中：m为板屈曲时沿x方向的半波数；n为沿y方向的半波数。根据薄板稳定理论及相关实验结果可知，当板沿y向只有一个半波时，板的临界屈曲应力最小，即n=1(张耀春等， 2011)；结合工程实际调查，m取1。则式(2)可简化为：

(3)

式中：f为板挠度的最大值。滑移段BC对弯曲段AB的下滑推力记为F，这是使弯曲段AB产生挠曲的原因之一。假设主滑面层间结构面黏聚力为C，摩擦角为Φ，则推力F为：

F=(L-lcr)b[γh(sinα-cosαtanΦ)-C]

=(L-lcr)bT

(4)

式中：T=γh(sinα-cosαtanΦ)-C(当T≥0才可能出现弯曲失稳)；γ为岩板的重度；α为岩层倾角。在三峡库区实际岸坡中，由于岩层结构面及岩体力学参数受库水位多场耦合劣化损伤，呈现动态下降趋势。根据前期研究将岩体参数通过广义Hoek-Brown中GSI(t)函数建立与时间t的关系(殷跃平等， 2020)，也即岩体强度指标tanΦ、C、E为GSI的泛函：

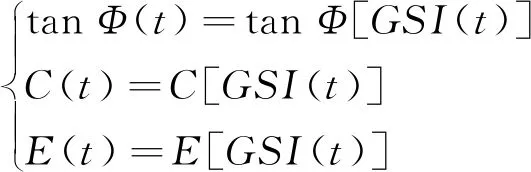
(5)

结合文献(殷跃平等， 2020)以及广义H-B准则(Hoek et al.，1997； Hoek et al.，2002；韩凤山， 2004； Hoek et al.，2019)，GSI与M-C准则在适用范围内可进行等价互换，其相关公式如式(6)：

(6)

式中：σ3n=σ3max/σci，σ3max是对应实际岸坡应力环境围压σ3的最大值；Ei为完整岩石的变形模量。σci为无侧限单轴抗压强度，mi为完整岩石的材料常数。A、B为根据现场跨孔声波测试所得的主滑面实测拟合参数。e为自然对数，mb(t)、s(t)、a(t)为与GSI相关的参数，可根据现场跨孔声波测试数据与Hoek-Brown准则推导可得(Hoek et al.，2019；殷跃平等， 2020)。将式(5)、式(6)代入式(4)中可得下滑推力F(0)(库区岸坡后缘岩体不考虑劣化，仅坡脚处劣化损伤，故后缘F将t=0代入)：

F(0)=(L-lcr)b[γh(sinα-cosαtanΦ(0))-

C(0)]=(L-lcr)bT(0)

(7)

2.2 基本公式推导

在薄板小挠度弯曲问题中，εz、γzx、γzy可忽略不计，利用能量法对顺层边坡滑移弯曲失稳问题进行近似分析。能量法实质是指：在平衡状态下，外力对系统所做的功等于系统内部应变能的增加，即：

δU=δW

(8)

由能量法可知，板的应变能U求解如下：

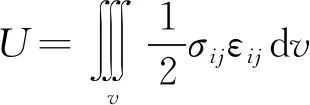
(9)

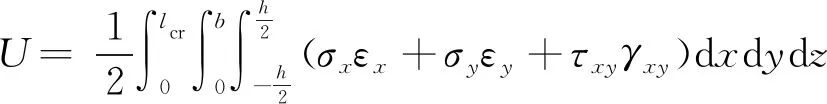
(10)

根据薄板小挠度屈曲理论，只取挠度ω(x，y)作为基本函数求出主要应变分量与主要应力分量如下：

应变分量：

(11)

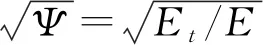
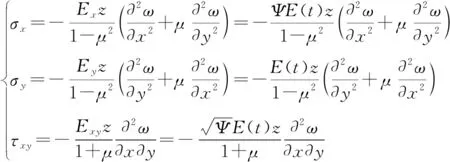
(12)

将上述应变分量、应力分量代入式(10)中整理化简有：

(13)

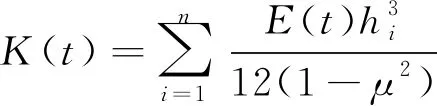
(14)

由能量法原理知外力做功为：

(15)

(16)

式中：σx，σy，τxy均为板中平面(z=0)的外力。其中正应力以压为正，剪应力以板的中面相邻两边夹角增大时为正。在不考虑其他外部力的作用下，仅考虑由坡体自重产生的变形做功。则由力学模型可知岩板仅受下滑力F和自重G作用，其他力σy=0，τxy=0。根据弹性理论z方向的重力分量远小于其他3个应力分量可以忽略。则σx的表达式为：

(17)

将式(3)、式(17)代入到式(16)化简可得：

(18)

此处板无初始变形，板中增加的弹性势能即为板因弯曲变形而产生的全部内能如式(14)。F和G的分量作功为外力功如式(18)。将式(14)和式(18)代入到式(8)有：

(19)

将K(t)值代入上式整理可得：

(20)

σcr=σT

(21)

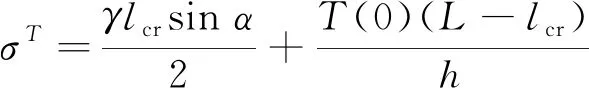
(22)

将边坡的物理力学几何参数代入式(22)，通过求解方程即可得岩板临界挠曲段lcr，进而确定边坡滑移段长度L-lcr。本文计算模型将岩体劣化概念t引入，对物理力学参数E(t)进行动态折减。岩体实时动态劣化最终体现在岸坡临界挠曲段lcr与稳定状态的衰减上。即使边界条件不变，由于趾部弯曲段lcr等效抗弯刚度K(t)逐渐减小而减小。如不考虑岩层塑性以及岩体劣化的影响(即E不变且Ψ=Et/E=1)，则刘小丽等(2002)基于弹性板法推导的平衡方程可视为本文推导式(22)的特定解，可见本文推导公式考虑了岩体动态劣化，将劣化时间t引入，其应用范围更广。

3 考虑岩体劣化效应的顺层滑移-弯曲实例

表1 本文方法与不同典型方法对比

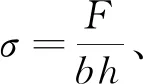
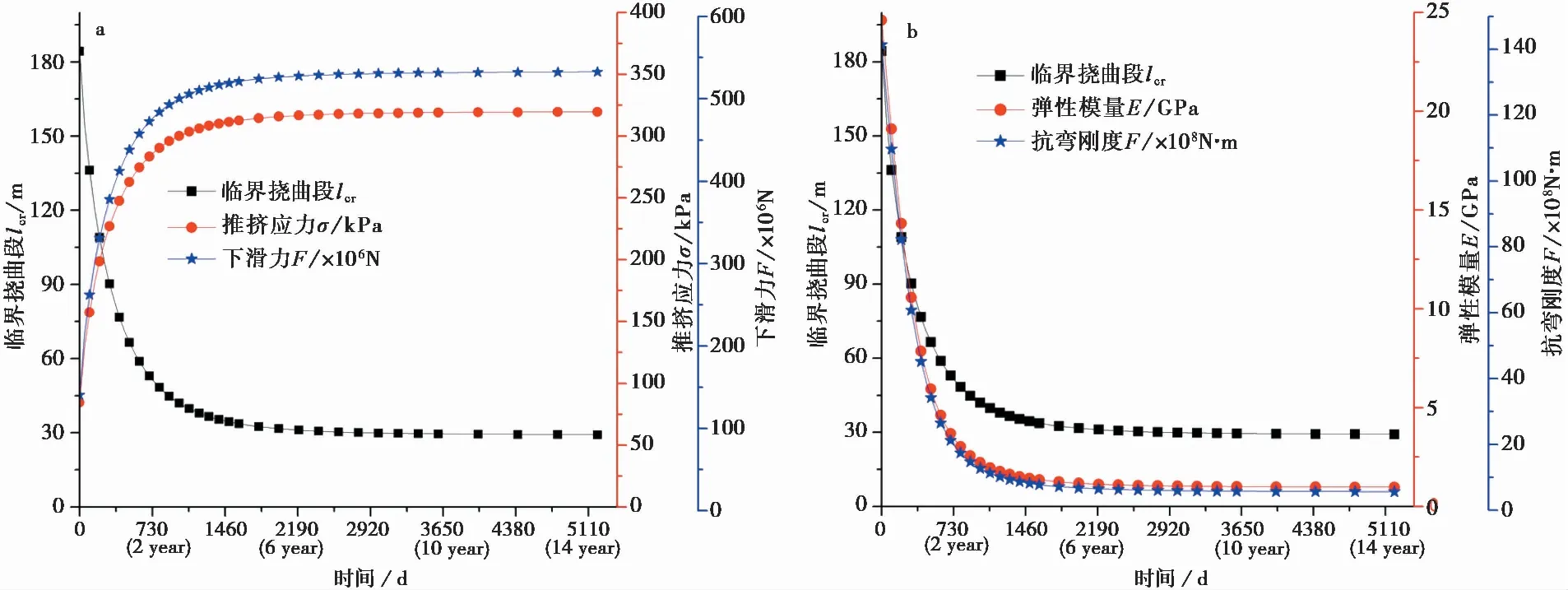
图4 随劣化时间t临界挠曲段与各参数变化对比

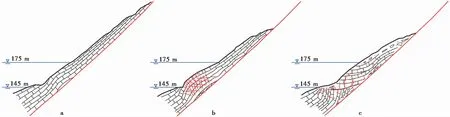
图5 滑移-弯曲型滑坡演化过程(据张倬元等(2009)修改)

4 讨论

为了探讨岩层倾角α以及岩层板厚hi对临界挠曲段lcr的影响，取劣化时间t=3600d(约为10year的劣化)对应参数进行计算，设定不同岩层倾角α(取α=10°、20°、30°、35°、40°、43°、45°、50°、60°、70°、80°、90°)以及岩层厚度hi(取hi=0.2m、0.3m、0.4m、0.5m、0.6m、0.7m、0.8m、0.9m、1m、1.1m、1.2m、1.3m、1.4m)进行探讨对比，其他参数同上述文中案例，具体计算结果见图6。

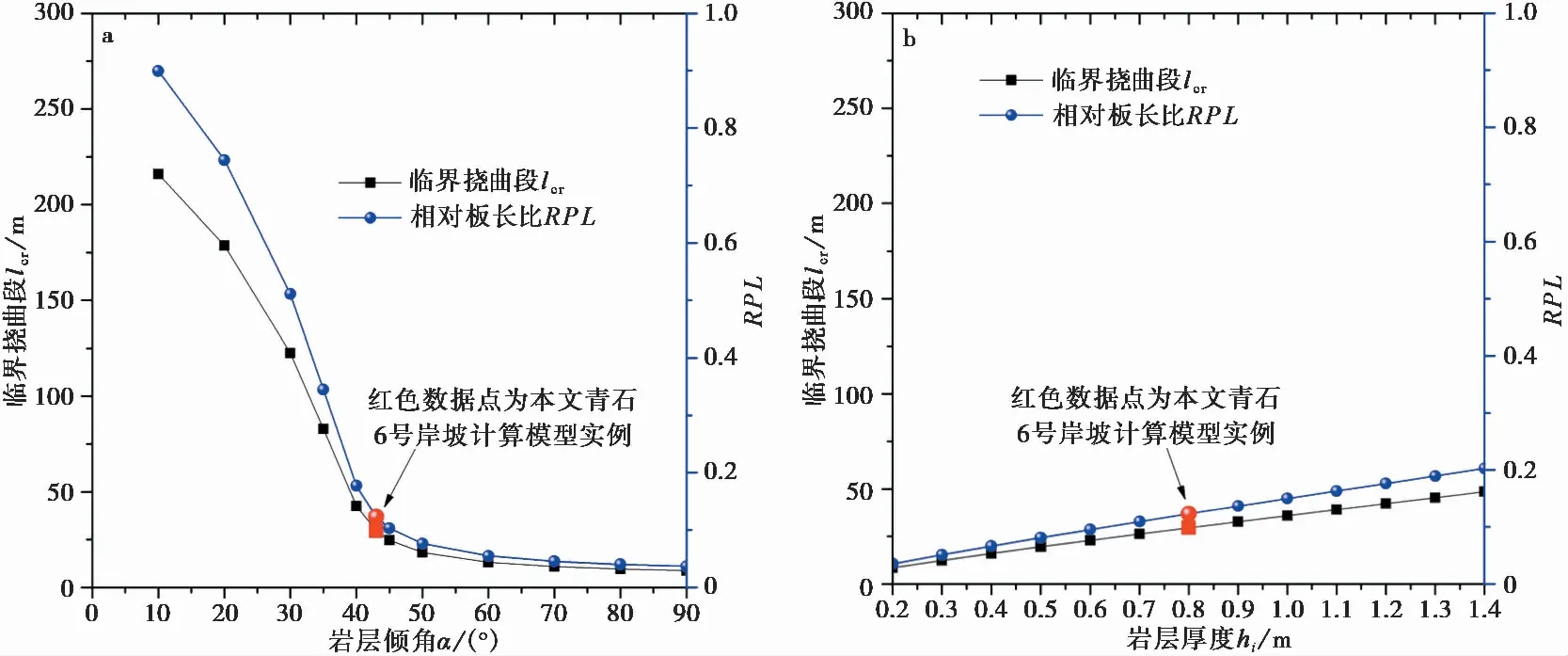
图6 岩层倾角α与厚度hi对临界挠曲段lcr及相对板长比RPL的影响(t=3600d)

由图6可知随着岩层倾角α增大，临界挠曲段长度lcr与相对板长比RPL呈近似指数形式的快速降低；随着岩层厚度hi增大，临界挠曲段长度lcr与相对板长比RPL呈近似线性缓慢变大趋势；且对比两者，岩层倾角α对临界挠曲段长度lcr与相对板长比RPL的影响明显大于岩层厚度hi的影响，即岩层倾角α对岸坡稳定性影响的敏感性远大于岩层厚度hi，这一发现与孙广忠等(2011)、刘云鹏(2017)研究一致。分析认为：在其他参数恒定的情况下，随着岩层倾角变陡，岩板自重产生的沿岩层面向下重力分量快速增大，而垂直于岩板的法向分量却迅速减小，两方面因素促使下滑力F快速增大，不利于岸坡稳定。随着岩层厚度hi增大，岩板的多层板等效抗弯刚度K明显增大，有利于岸坡的整体稳定。且由图6a可知岸坡临界挠曲段lcr快速下降角α在40°～60°，可作为三峡库区青石-抱龙段顺向岸坡是否容易滑移-弯曲失稳的一个地质判据。当α=0°时模型变为水平简支梁模型，不会发生滑移-弯曲破坏且不适用于本文计算模型。对于图6b则没有明显的转折点，随层厚hi增大整体主要呈近似线性变化情况。

对于此类顺层“滑移-弯曲”失稳岸坡的防治，需结合上述岩体劣化失稳演化进程中两大促发因素：针对岸坡趾部软化进行挠曲段的加固、后缘滑移段下滑力传递力链的阻断。特别是“关键区段”的加固，避免挠曲段向上扩展演化，对整个岸坡的稳定状态至关重要。同时若仅仅进行挠曲段加固，由于后缘滑移段下滑挤压推力的存在，容易造成弯曲段“上移”，因此需间隔一定距离对后部滑移段下滑力链进行截断。综上建议对趾部岸坡劣化带区域可采用“喷浆+挂网+锚索(杆)”加固，同时对后部滑移段建议采用间隔一定距离“锚索(杆)”或“格构拱圈”加固阻断力链传递的综合治理方式。