基于多元函数极值理论巧证几个三元不等式
2021-07-19范铭灿
范铭灿
(惠州学院 数学与统计学院,广东 惠州 516007)
三元不等式证明是中学数学竞赛中的常见题型,其证明方法通常需要使用均值不等式、Cauchy-Schwarz不等式、Schur不等式、Hölder不等式和Jensen不等式等[1], 甚至是这些方法的综合运用, 是一类高难度的数学题目.目前关于利用多元函数极值理论证明三元不等式的研究较少[2-5], 这可能是因为大多数情况下多元函数极值点的验证较为复杂. 本文基于几道典型例题,说明如何结合若干不等式技巧以及多元函数极值理论证明三元不等式, 从而拓展三元不等式的证明思路.
1 变量代换法
例题 1证明:对所有正实数a,b,c,有
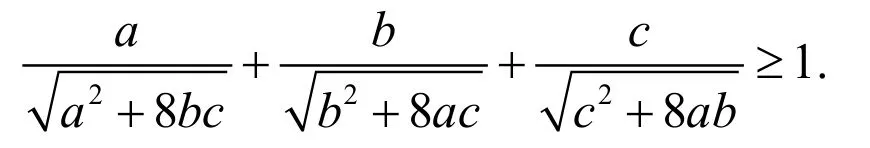
这道题目是第42届IMO试题.如果直接对不等式左式的多元函数(a,b,c看成自变量)求极值,会发现其驻点求解非常繁琐,并且无法验证驻点是否为极值点(Hessian矩阵奇异). 为了解决这一问题,本文利用变量代换的方式将不等式转化为二元函数极值问题.
证明令则构造二元函数如下:
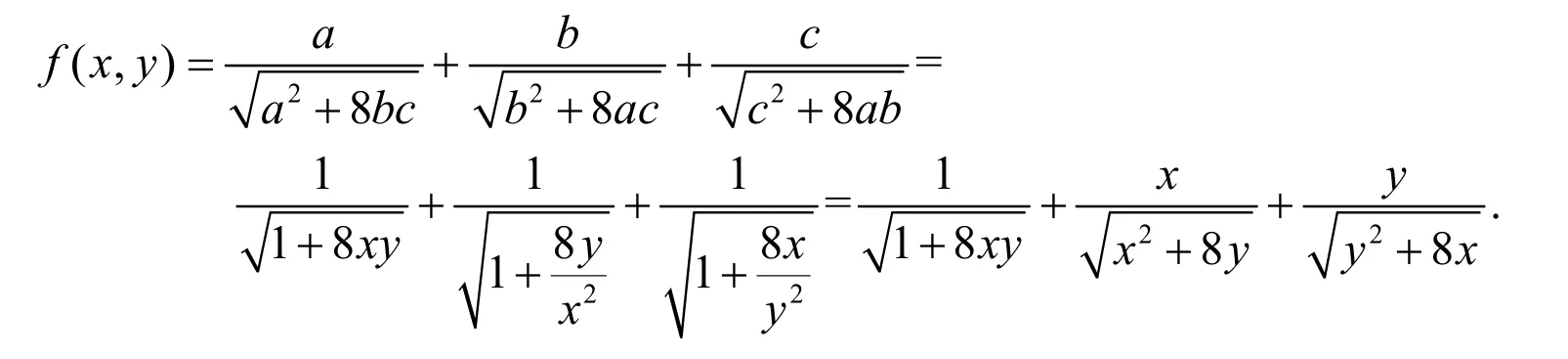
为了求出函数f(x,y)的驻点,令
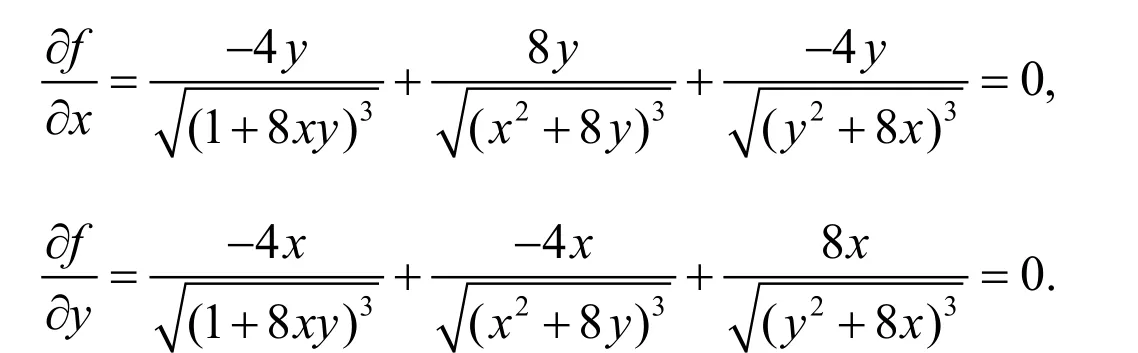
为了验证驻点是否极值点,算出函数f(x,y)的二阶偏导数如下:
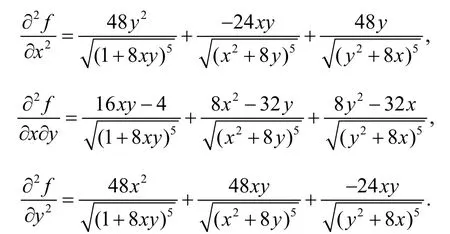
代入(x,y)=(1,1),得到Hessian矩阵,其为正定矩阵,这说明(1,1)为极小值点,极小值为f(1,1)=1.类似可证明(7,1)为非极值点,(1,7)为极小值点,且极小值为对比2个极小值可以得到f(x,y)≥f(1,1)=1. 证毕.
2 不等式放缩法
例题2证明:当0≤a,b,c≤1时,函数
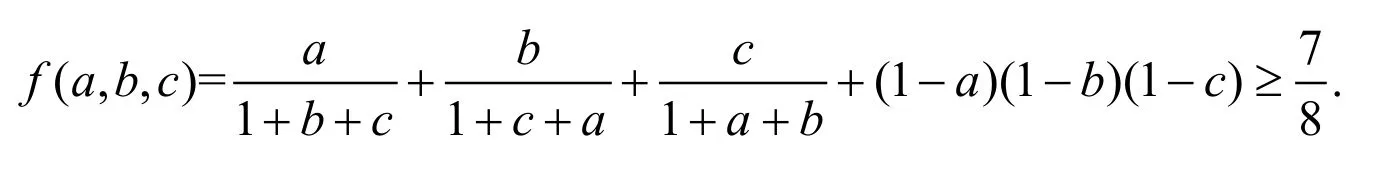
这道题目改编自一道美国数学竞赛题,具有一定难度. 文献[6-7]针对该问题分别给出了不同的证明方法. 本文利用不等式放缩法结合多元函数极值理论,给出一个较为简便的证明.
证明如果直接将a,b,c直接看成变量,对函数f(a,b,c)求极值,会发现求解驻点非常困难.为此,首先将函数做放缩如下:

其中用到了算数-调和平均值不等式,等号当且仅当a=b=c时成立.
令 1-a=x,1-b=y,1-c=z,构造一个新的函数如下:

令

由式(1)、(2)、(3)易得x=y=z(同时也说明a=b=c).将此等式代入式(1),可得于是,函数g(x,y,z)的驻点为(x,y,z)=(1,1,1),或者
由于函数g(x,y,z)在[0,1]×[0,1]×[0,1]上必有最小值,则将函数值与其他端点的函数值作大小比较,从而得到函数g(x,y,z)的最小值为因此,函数f(a,b,c)的最小值为证毕.
3 拉格朗日乘数法
例题3证明:若x,y,z为非负实数,且满足等式x+y+z=1,则
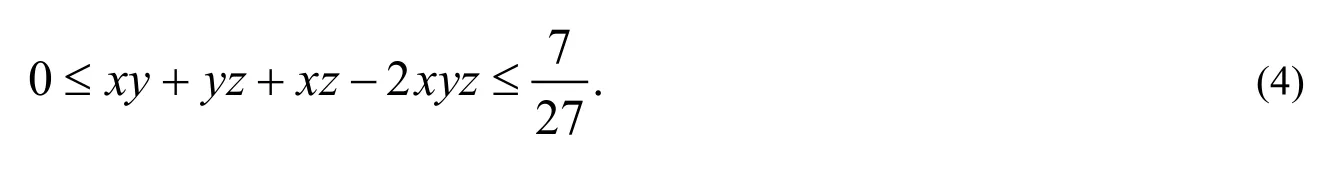
这道题目是第25届IMO试题,本文利用多元函数的条件极值理论进行证明.
证明引入拉格朗日乘数λ,构造辅助函数g(x,y,z)如下:

下面只需证明函数g有最小值0和最大值即可.
首先求函数g(x,y,z)的驻点.令
由式(5)、(6)可得(x-y)(1-2z )=0.由式(6)、(7)可得(y-z)(1-2x)=0. 结合式(8),可求得函数g的驻点为其对应的函数值分别为由于连续函数g在[0,1]×[0,1]×[0,1]上必有最大和最小值,并注意到端点(1,0,0),(0,1,0),(0,0,1)的函数值均为0,可以直接得到式(4).证毕.
4 参数代换法
例题4证明:若,,a b c为任意实数,则
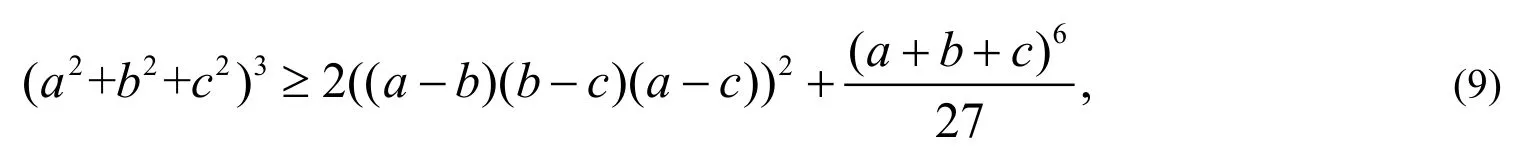
并说明等号何时成立.
这道题目来源于文献[8],是加拿大数学学会创办的数学难题期刊《Crux Mathematicorum》上的题目, 尚未有解答. 本文利用参数代换法并结合多元函数极值理论进行证明.
证明首先作变量替换,令a -b =x,b -c =y,a +b +c =z,则a-c=x+y,且
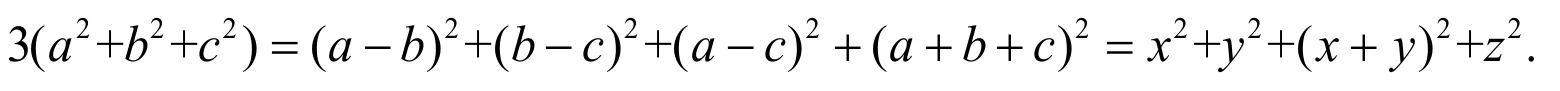
于是,证明式(9)等价于要证明如下不等式成立:
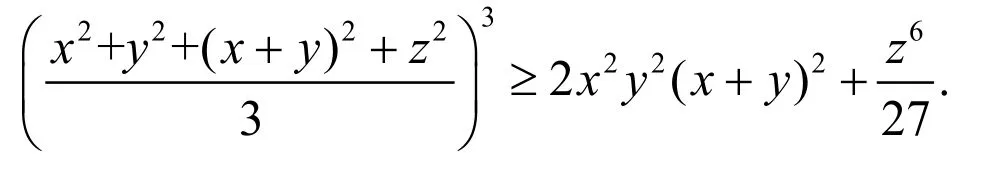
即证明
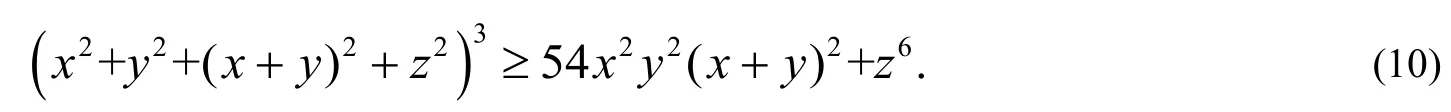
显然,当x =y=0时等号成立.当xy=0时,不等式也显然成立.下面只需考虑xy≠0的情形.不妨设a>b>c,即x>0,y>0. 其他情形可类似证明.
直接利用极值理论证明不等式(10)会非常困难,原因是Hessian矩阵为半正定矩阵,无法判断驻点是否为极值点. 这里采取引入参数的方法,进一步利用条件极值理论给出证明.
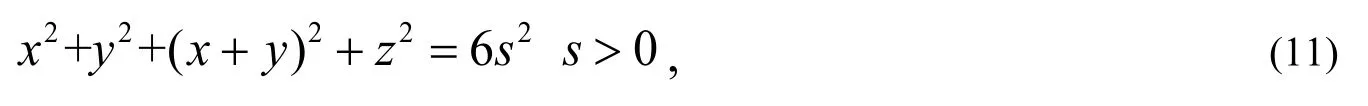
时取得极大值216s6即可,其中s表示一个未知的正参数.
引入拉格朗日乘数λ,构造函数如下:
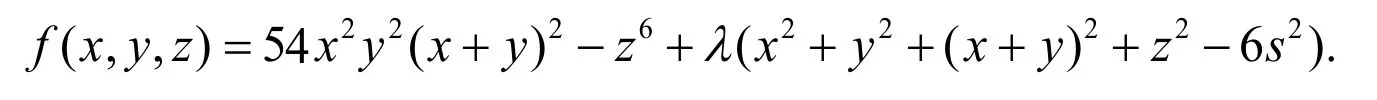
令
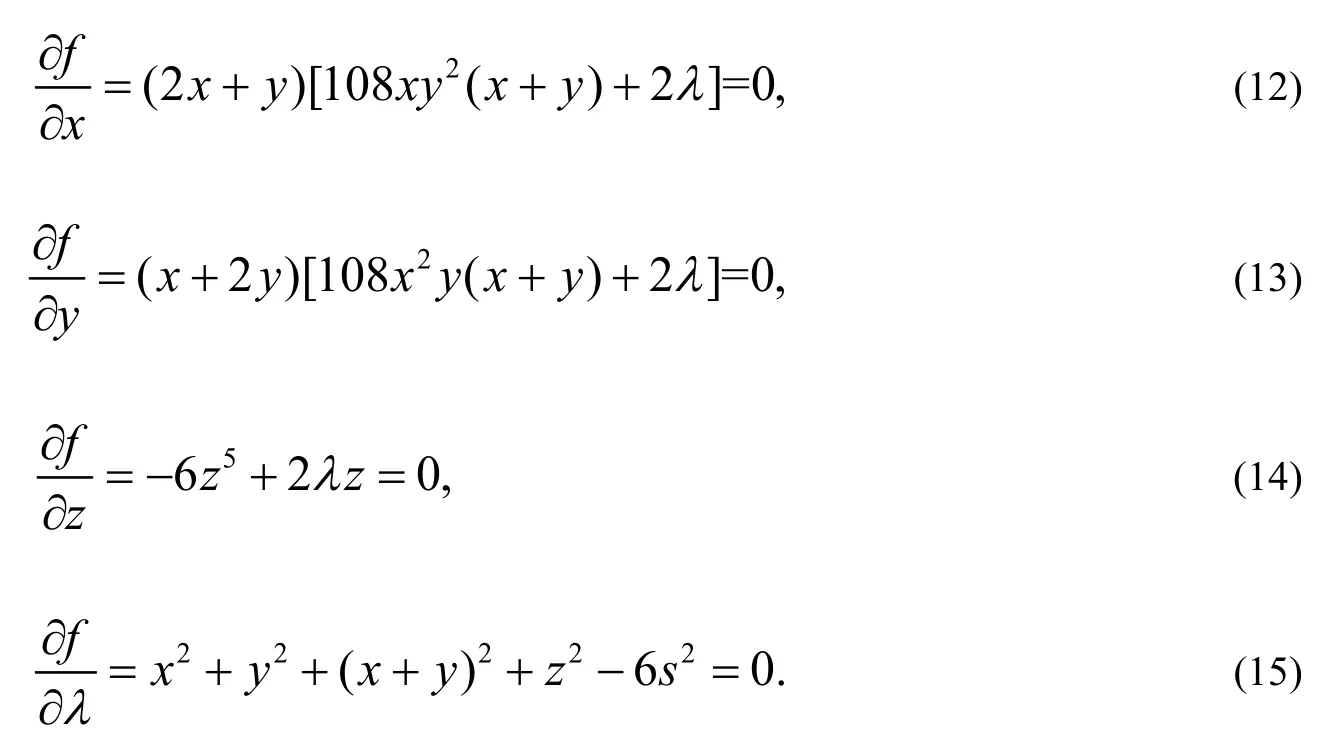
进一步,基于驻点x,y=且0,z=以及式(9)中a,b,c的轮换对称性,得到式(9)等号成立的全部条件为a=b=c,或者a+c=2b=0,或者a+b=2c=0,或者b+c=2a=0.
5 结论
本文基于多元函数极值理论, 介绍了三元不等式的几种证明方法. 可以发现: 在证明复杂的三元不等式过程中往往不能通过直接构造多元函数, 进一步求解其极值来证得, 而是需要一些辅助手段和技巧构造合适的多元函数, 其主要目的就是使得该函数的极值求解会更容易. 另外, 相比于其他不等式放缩方法, 利用极值理论证明不等式可以很方便地得到不等式等号成立的条件.
