基于刚柔耦合环模型轮胎均匀性建模与分析

危银涛，刘 哲，2，魏 胜，蔡志兴，路 波

（1.清华大学 车辆与运载学院，汽车安全与节能国家重点试验室，北京 100084；2.慕尼黑工业大学 机械工程系，车辆系统声学研究所，慕尼黑 85748；3.山东玲珑轮胎股份有限公司，山东 招远 265400）

轮胎在汽车动力学及噪声、振动与声振粗糙度（NVH）分析中占有重要地位。随着人们对车辆行驶速度、安全性、舒适性、操控性能要求的提高，对轮胎动力学响应进行精细化分析也提出了更高要求[1]。轮胎动力学不仅影响整车动力学响应，同时也在防抱死刹车系统（ABS）、车身电子稳定系统（ESP）等汽车电控系统中扮演重要角色。因此，建立一个准确并可快速计算的轮胎动力学模型不仅可以为传统整车NVH分析过程提供理论基础，同时也可以更好地推进轮胎及底盘技术的电动化和智能化。

在汽车及轮胎动力学分析中，通常会将轮胎假设为理想的结构。事实上，考虑到轮胎生产所需的多种制造材料的组合以及复杂的工艺流程，轮胎在制造过程中会不可避免地产生结构以及材料分布的缺陷，例如径向尺寸偏差、质量分布不均衡、胎侧刚度不均匀以及带束层偏歪等[2]。这些非理想的因素，即轮胎的均匀性参数会导致轮胎在稳态滚动状态下依然可能引起轴力变化，并通过不同的车辆子系统和车身结构传递给驾乘人员。这部分由轮胎均匀性引发的振动可能是方向盘抖动、车身振动和部分车内噪声产生的根本原因。而这些异常振动往往会影响车辆的平顺性和驾驶质量，并对车内人员造成干扰。因此讨论轮胎均匀性参数所产生的影响具有理论意义和广泛的应用价值。

如何提高轮胎均匀性一直是国内外轮胎企业关注的核心问题。从20世纪70年代开始一些轮胎厂就开展了相关研究。1974年邓禄普轮胎公司研究了一批轮胎的一次谐波随速度的变化规律，重点讨论了纵向力与径向力随速度变化的相位和幅值关系[3]。1989年费尔斯通轮胎公司利用概率统计的方法对轮胎的一次谐波分布和均匀性参数进行了分析，并对轮胎均匀性的分布曲线进行预测，包括均值和标准差[4]。1990年，普利司通公司并购费尔斯通轮胎公司后，进一步研究了车轮角速度与均匀性参数导致的轴力波动之间的关系[5]。1993年，现代汽车公司也研究了由于轮胎质量分布不均衡导致的方向盘抖动问题[6]。固特异公司利用高速均匀性试验机对轮胎径向力和切向力的一阶谐波进行了测试[7]。2001年国内的上海轮胎橡胶（集团）股份有限公司采用有限元分析方法对轮胎几何形状和材料缺陷引起的径向力变化进行了预测[8]。2005年，韩泰轮胎公司发表了一系列关于轮胎均匀性研究的论文[9-11]，其考虑了质量不平衡、刚度和几何不均匀等因素，并分析了轮胎共振对轴力幅值的影响，进而利用试验数据进行了验证，最后利用FTire模型进行了仿真数据的对比，同时讨论分析了轮胎几何不均匀造成方向盘抖动的传递机理。但是大多数轮胎企业的研究是基于大量轮胎样本和测试数据进行统计分析，这种分析方法不仅成本高，而且很难实现由均匀性测试分析到轮胎结构优化、生产工艺流程控制以及轮胎动态响应性能的改进。

因此，很多学者都建立了相应的理论物理模型，用以描述轮胎均匀性参数的影响。T.D.Gillespie[12]最初基于大量试验数据，利用简化的弹簧-质量系统来解释轮胎-车轮系统的均匀性对重型卡车驾驶质量的影响。但是由于这种物理模型对轮胎结构采用了过于简化的假设，因而并不能对轮胎均匀性参数进行很好的描述。基于刚性环的假设，D.S.Stutts等[13-14]解释了随着速度的提高，轴头纵向力的增大速度快于垂向力的现象，并在此基础上，进一步研究了胎侧附加的集中刚度对径向力波动的影响。D.S.Stutts等[13]同样采用了刚性环模型，对带束层质量分布不均及偏心、胎面胶厚度变化进行了分析，并与FTire模型的仿真结果进行了对比。B.L.Dillinger等[15]在D.S.Stutts等工作的基础上，结合胎侧胶的粘弹性模型[16]及纵向力松弛模型[17]，分析了不同速度下质量不均匀、刚度不均匀以及径向尺寸偏差对切向力和径向力的影响。M.G.Pottinger[18]总结了质量不均匀对轮胎-轮辋系统的传递特性的影响，并提出了由于组件安装不均匀导致轴力响应的改进方法。虽然轮胎均匀性对轮胎结构设计及整车动力学分析都有重要的影响，但是由于轮胎结构、材料的复杂性，过去大多数研究都集中在使用刚性环模型对轮胎的均匀性进行分析。由于刚性环的变形限制，只能采用非常简化的模型对均匀性参数进行描述，例如采用一个整体偏心量或采用简单的函数描述几何偏差等。这种模型本身的局限性使得现有物理模型只能对各类不均匀参数进行简单的定性讨论，或者通过大量试验数据进行统计分析。

因此，本工作的目的是建立一个实现分析径向尺寸偏差引起的轮胎动力学响应的理论模型，用以分析轮胎均匀性参数对轴头力的影响以及力的传递机制。在轮胎环模型[19-20]的基础上，本研究建立了刚柔耦合环模型，利用柔性环模型讨论分析了轮胎与路面之间的接触机理，从而在模型中引入均匀性参数，利用刚性环模型对轮胎的动力学响应进行描述，并建立柔性环与刚性环的耦合关系，得到完整的轮胎动力学响应的算法及计算流程；进而给出了模型参数的辨识方法以及基于低速均匀性试验数据的参数优化方法；最后利用提出的轮胎均匀性分析模型，对径向尺寸偏差导致的轴头径向力波动进行了时域和频域分析，并与试验数据进行对比和分析，显示了仿真结果与实测结果良好的一致性，从而验证了提出的理论模型与仿真算法的有效性及准确性。

1 轮胎刚柔耦合环模型

长期以来如何对轮胎进行物理建模，简洁而不失准确性地描述其物理特性都是汽车动力学分析中的关键问题。自20世纪60年代起，将充气轮胎简化为环模型的方法得到了广泛应用。环模型在保留对轮胎基本结构描述的同时，保证了简洁的数学求解方法。为了分析车轮平面内由于均匀性参数导致的动态响应，将轮胎等效为二维环模型[19-20]。以往关于轮胎环模型的研究可分为刚性环模型和柔性环模型两类。刚性环模型自由度少、计算速度快，但是对轮胎-路面接触的描述存在缺陷，需要通过建立等效路面的方法实现接触力的计算。柔性环模型对轮胎物理特性的描述更接近实际结构，并且仿真可实现的频率范围可以达到120 Hz，但是模型复杂程度较高。

为了实现对轮胎均匀性参数的分析，要求模型具有能够描述轮胎结构及材料属性的能力。因此提出轮胎刚柔耦合环模型，首先利用柔性环模型对轮胎的变形及接触特性进行理论建模，得到轮胎稳态变形及接触力的计算方法；同时利用刚性环模型对轮胎的整体运动及动态响应进行描述；最终建立这两种环模型之间的耦合关系，给出完整的刚柔耦合环模型的理论表达与计算流程，为实现轮胎均匀性参数分析奠定理论基础。

1.1 二维柔性环模型

二维柔性环模型主要由3部分组成：轮胎的带束层结构及胎体部分等效为一个二维可变形的圆环，它可以在车轮平面内产生弯曲变形；胎侧部分及充气效应假设为一个有阻尼的弹性基础，空气对轮胎内表面施加均匀的压力分布，并采用径向和周向分布弹簧（弹性系数分别为ku，kv）模拟弹性基础的弹性特性，在模型中引入径向和周向阻尼系数（cu，cv）来描述胎侧的阻尼效应；轮辋假设为刚体。将轮胎转化为弹性基础上的二维可变形环的方法如图1所示。

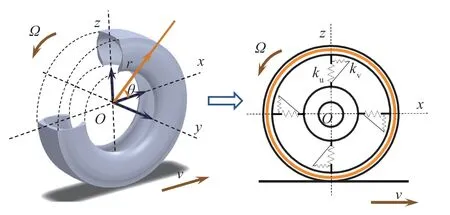
图1 轮胎二维环模型形成示意

考虑到轮胎的高速滚动，需要建立合适的坐标系来描述轮胎变形，车轮中心选为坐标系原点。环上任一点的坐标在非旋转坐标系中可以用极坐标系（r，θ）来表示，或者在旋转坐标系（r，φ）中进行描述。环上任一点的位移由径向位移（u）和周向位移（v）表示，它们也是环中面上的位移的函数。文献[21]中给出了用中面切向位移（vb）表示的环的运动方程。假设胎体和带束层被等效为一个周向不可伸长的环，中面上任一点的径向位移ub和vb满足下式：

将环的切向位移用模态展开，得到

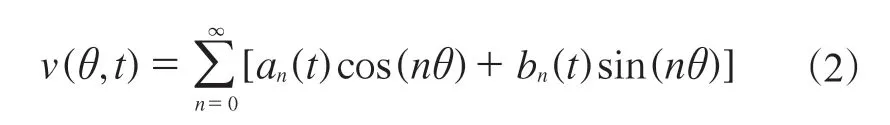
式中，t为时间，n为态展开的阶次。

在广义坐标[an（t），bn（t）]下，运动方程可简化为线性二阶微分方程组：

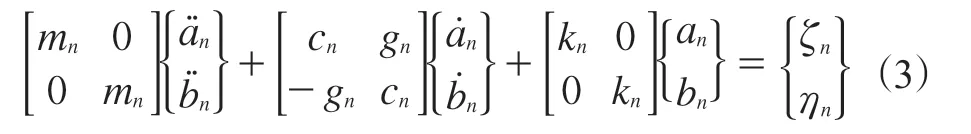
式中，ζn和ηn分别为与径向和切向集中力以及力矩对应的广义力。矩阵元素表示如下：

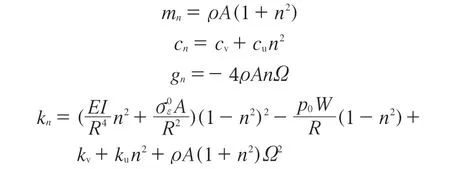
式中，ρ为环的密度；A为环的截面积；Ω为轮胎的旋转速度；E为环的等效弹性模量；I为环的截面惯性矩；R为平均半径；为环中由胎压p0和旋转效应导致的初始应力；W为带束层宽度，即环的等效宽度。

在非旋转坐标系下，当φ0处施加一组径向和切向集中力以及力矩（qu，qv，qβ），可采用待定系数法求得胎体的稳态响应：

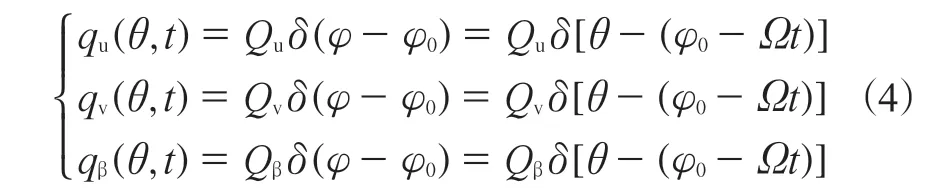
式中，Qu，Qv及Qβ表示作用在胎体上的一组径向、切向集中力及力矩的幅值。

对环进行离散化，通过对各点响应进行叠加即得到柔性环的整体位移。径向位移和切向位移的表达式为

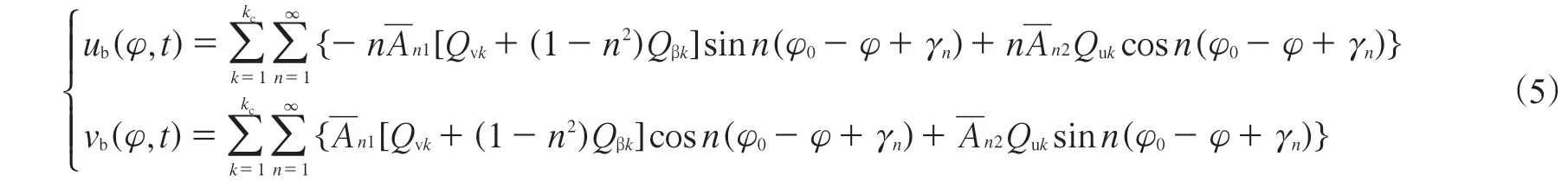
式中系数表示如下：

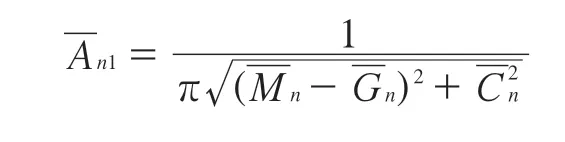
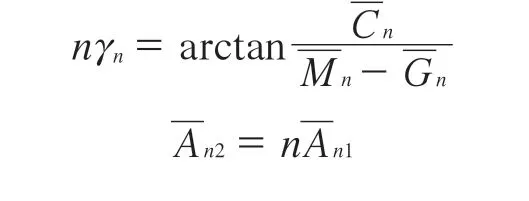
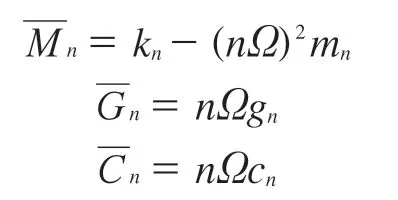
式（5）可使用矩阵形式表达：

式中，U为胎体的位移矩阵，T为柔度矩阵，Q为广义力矩阵。

给定作用在胎体上的广义力（qu，qv，qβ）后，胎体中面位移（ub，vb）可由式（5）计算得到，进而求得柔性环中任一点的位移。

1.2 接触力

由于胎体与路面没有直接接触，因此胎体实际产生的变形是未知的，故不能直接利用式（5）计算胎体位移。当胎面与地面接触时，胎体与胎面胶的位移应满足几何相容性条件[12]。在确定的垂向位移（下沉量）下，胎体截面转角（β）表示为

柔性环与路面接触后的曲率变化可由变形前后的法线偏角（α）来表示，并且法线偏角同时会影响胎面胶的切向变形。在给定的下沉量下，胎面胶的法向和切向变形（us，vs）及在任意坐标φ处的α可由下式表示：

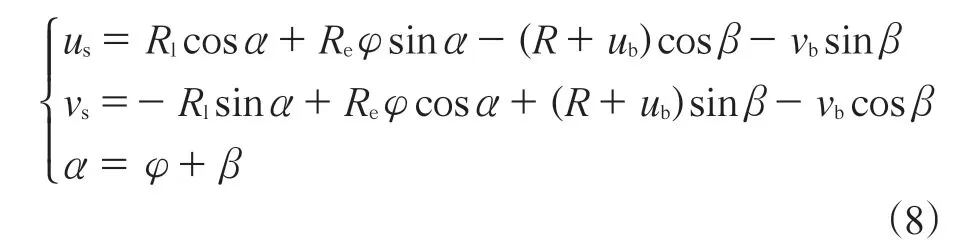
式中，Rl为轮胎的动力半径，即路面到轮胎轴头的高度；Re为轮胎的有效滚动半径。

计算得到胎面位移后，作用在胎面上的法向力（Fns）和切向力（Fts）可由下式给出：

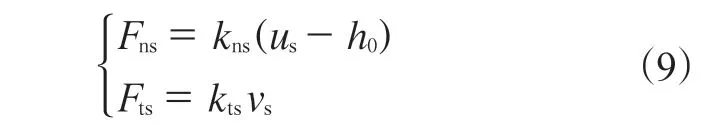
式中，kns和kts分别为单位长度胎面胶的法向刚度和切向刚度，h0为胎面胶变形前的厚度。

利用坐标变换方式，可以得到作用在胎体上的广义力以及接触区域内的法向压力（σ）和剪切力（τ）。

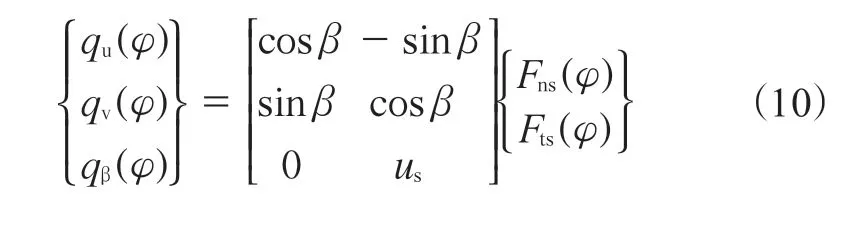
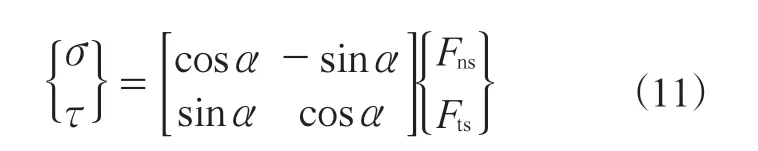
采用胎体小变形假设，将式（8）和（9）代入式（10）并转化为矩阵形式，胎体变形的线性化方程可表示为

式中：F为与胎面胶变形相关的广义力矩阵，其中参数与U无关；H为与胎体位移相关的系数矩阵，其中包含胎面胶刚度系数与胎体位移的耦合项。

得到下沉量后，便可采用逐次迭代的方法得到精确的接触力，并将其作为刚性环模型的激励输入，从而计算轮胎的瞬态响应。

1.3 刚性环模型

如果完整地建立一个考虑轮胎弹性变形和旋转效应的动力学模型，会使描述运动的偏微分方程过于复杂而难以求解。因此，当轮胎在车轮平面内的振动频率在100 Hz以内，即在轮胎的一阶模态范围内时，轮胎的胎体及带束层保持为刚性环，做整体运动，从而可以近似描述轮胎的瞬态响应。

刚性环包括胎面、带束层、胎体以及部分胎侧。刚性环与轮辋之间由三自由度（纵向、垂向、周向旋转）弹簧连接，并考虑胎侧的阻尼效应，如图2所示。

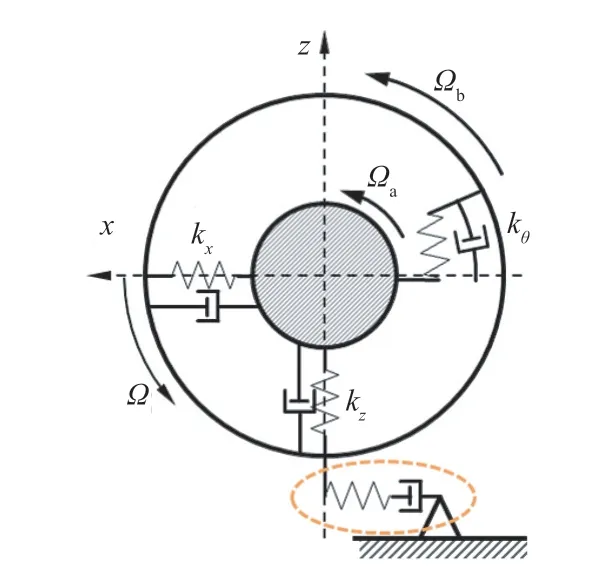
图2 刚性环模型示意

考虑刚性环平面内的3个自由度（xb，zb，θb）以及轮辋平面内的3个自由度（xa，za，θa），当车轮速度恒定时，轮辋纵向自由度（xa）可以由车辆速度确定。

平面内刚性环及轮辋的运动方程为

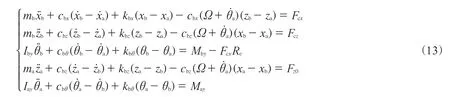
式中，ma和mb分别为轮辋和刚性环的质量，kbx和cbx分别为胎侧纵向等效刚度及阻尼系数，kbz和cbz分别为胎侧垂向等效刚度及阻尼系数，kbθ和cbθ分别为胎侧周向等效刚度及阻尼系数，Fcx和Fcz分别为轮胎的纵向和垂向接触力，Iay和Iby分别为轮辋和刚性环的转动惯量，Fz0为轮胎的垂向负荷，May和Mby分别为轮辋和刚性环绕y轴的转矩。

刚性环的模型参数可以通过一阶模态试验或Cleat试验结果进行辨识。然而，模态试验得到的固有频率相对Cleat试验结果偏高[22]。产生差异的原因之一是两种试验采用的边界条件不同，即模态试验无负荷，而Cleat试验中不可避免地引入了滚动负荷的影响。另一种可能的解释是胎面胶在滚动过程中与路面发生接触从而出现动态硬化效应，而这在模态试验中不会发生。同时柔性环和刚性环两组不同的刚度参数也反映出轮胎动静刚度的差异。

1.4 刚柔耦合环模型

由于刚性环模型在轮胎-路面接触机理的表达上存在理论缺陷，因此希望构建柔性环和刚性环之间的耦合关系，提出刚柔耦合环模型用以描述轮胎的动态响应。该模型中柔性环模型用于计算轮胎的稳态变形与接触力，而轮胎的动态响应由刚性环计算，如图3所示。

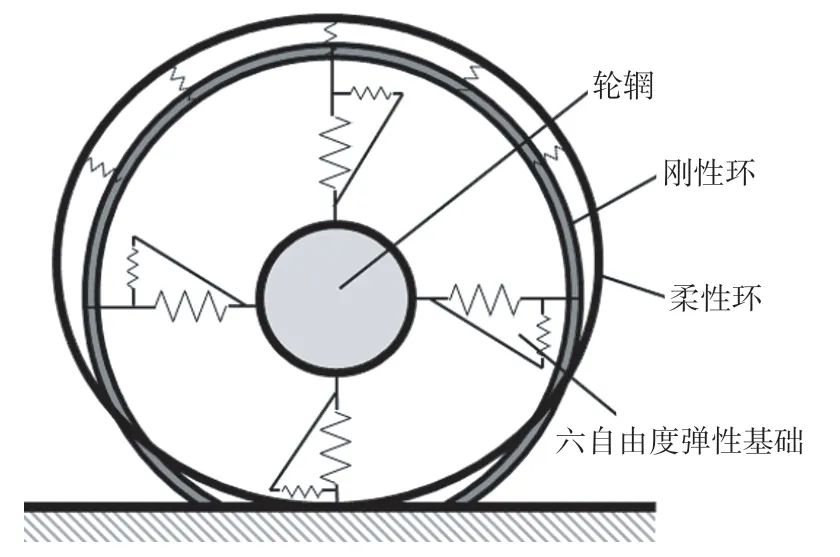
图3 刚柔耦合环模型示意

将刚性环方程与柔性环方程进行联立整合，从而得到完整的计算模型。将柔性环计算得到的接触力作为刚性环的激励，然后冻结瞬时环的位置，计算刚性环的整体位移和下一时间步的接触力，直至完成所有时间步的迭代。刚柔耦合环模型仿真流程如图4所示。

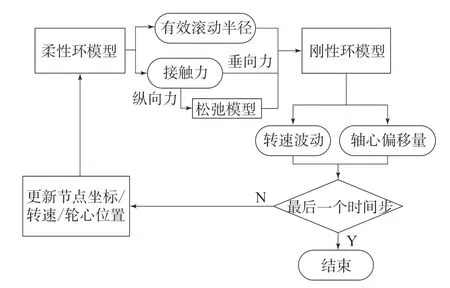
图4 刚柔耦合环模型仿真流程

1.5 不均匀性参数

结构和几何上的不均匀性会直接影响接触力分布，进而影响轮胎的动力学响应[23-24]。在柔性环模型中对几何尺寸偏差进行描述，并对其导致的接触力分布进行计算。由于几何不均匀在系统中产生了附加的广义力，会传递到刚性环模型中，进而影响轮胎的动力学响应。本研究考虑了轮胎制造过程中可能产生的几何不均匀性因素，即中心径向几何尺寸偏差（Radial Run-out of the Centerpoint，RROC），在后面仿真结果部分将讨论其对轴头径向力波动（Radial Force Variation，RFV）的具体影响。

2 模型参数辨识

为了验证提出的刚柔耦合环模型，选取了某品牌205/55R16子午线轮胎进行均匀性建模仿真及验证。刚柔耦合环模型的参数可分为结构几何参数和物理参数，其中一部分工程设计参数为：环等效宽度 0.172 m，环等效厚度 0.018 m，有效密度 1.6 Mg·m-3，平均半径 0.32 m，充气压力 0.21 MPa。这些参数也可以从有限元模型中获得。

由于轮胎结构简化为环模型，因此模型中物理参数的确定为仿真过程中的一个关键问题。物理参数可分为柔性环模型参数及刚性环模型参数两部分。在利用柔性环模型计算稳态响应时，使用模态叠加法求得胎体的稳态变形，进而利用胎面胶与胎体之间的几何协调关系求得接触力。在进行参数辨识时，采用轮胎模态试验所得到的各阶径向固有频率及一阶周向转动固有频率进行初步参数辨识。这部分工作在文献[20]中进行了推导和试验验证。对于刚性环模型中需要辨识的参数，利用模态试验得到的一阶固有频率，对等效刚度和阻尼系数进行辨识。

此外，针对目标轮胎，本研究采用遗传算法，选取一组RROC及对应的RFV试验数据对模型参数进行优化。基于模态试验辨识得到的参数作为初始输入，利用遗传算法逐次迭代优化模型参数，使仿真得到的RFV与试验数据的误差最小化。优化后的柔性环模型物理参数为：面内弯曲刚度1.69N·m-2，胎侧径向等效刚度 7.17×105N·m-2，胎侧周向等效刚度 1.73×105N·m-2，胎侧径向阻尼 226.89 N·s·m-2，胎侧周向阻尼 206.67 N·s·m-2，胎面胶初始等效厚度 0.015 6 m，胎面胶法向刚度 4.01×105N·m-1，胎面胶切向刚度 4.16×105N·m-1；刚性环模型参数为：刚性环等效质量 6.90 kg，弹簧纵向等效刚度 1.84×106N·m-1，弹簧垂向等效刚度 0.90×105N·m-1，弹簧周向等效刚度 3.23×103N·rad-1，纵向阻尼系数4.51×102N·s·m-1，垂向阻尼系数 1.32×103N·s·m-1，周向阻尼系数 19.36 N·s·rad-1。用于辨识的RROC数据及使用优化模型参数计算得到的RFV仿真结果如图5所示。

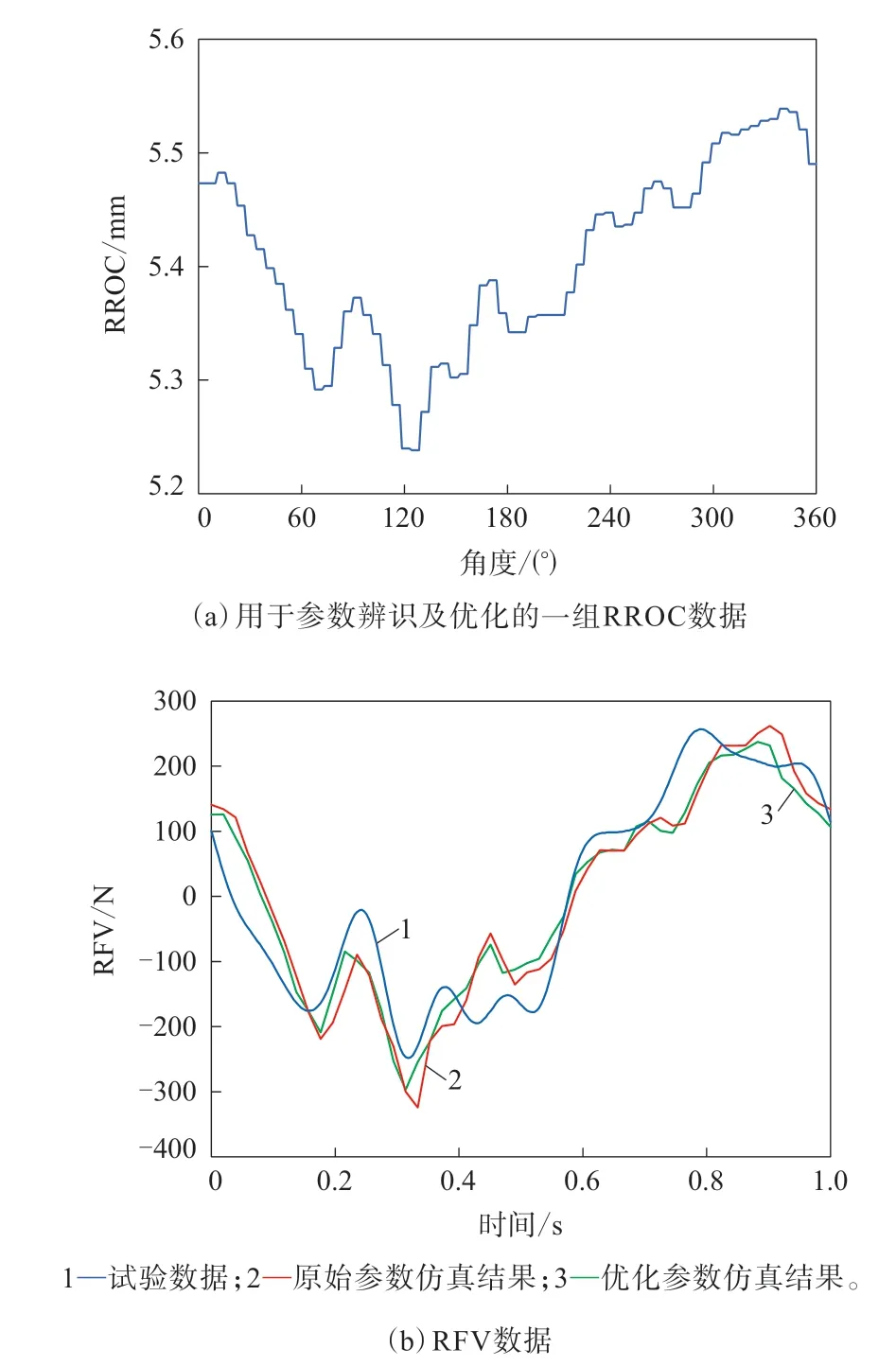
图5 利用遗传算法优化模型参数前后仿真结果与试验数据的对比

3 仿真结果及试验验证

基于上述刚柔耦合环模型及优化后模型参数，对目标轮胎在几何不均匀影响下的动态响应进行计算，从而分析和预测中心径向几何尺寸偏差对径向力波动的影响。

3.1 接地印痕内压力分布

在建立刚柔耦合环模型过程中，接触力是将柔性环和刚性环模型耦合在一起的关键，因此接触模型能否合理地表征轮胎-路面接触机理成为整个理论模型的核心。利用柔性环的稳态接触算法，对不同负荷下轮胎的接触力分布进行计算，以验证算法的合理性。

不考虑几何不均匀性并且假设路面为理想平面，不同垂向负荷下轮胎接地印痕内压力分布计算结果如图6所示。

从图6可以看出，柔性环模型可以很好地描述轮胎在不同负荷下的压力分布。在较小垂向负荷下，轮胎的接触压力呈抛物线分布；当垂向负荷逐渐增大时，接地印痕区中心部分有发生屈曲的趋势，导致垂向接触压力呈马鞍形分布。这说明柔性环模型可以很好地体现轮胎稳态接触时的物理特征，同时也验证了柔性环模型作为稳态变形及轮胎-路面接触模型的理论依据和合理性。

图6 不同垂向负荷下轮胎的接触力分布

3.2 考虑RROC的接触力波动

轮胎的几何不均匀主要导致接触力的变化。模型中假设胎面胶厚度变化是产生RROC的原因，这可以提高计算效率。为了将试验数据与柔性环的网格对应，需要对原始数据进行插值处理，进而在接触模型中引入其影响。一组轮胎外表面RROC的原始测试数据及插值后的曲线如图7（a）所示。为了模拟低速均匀性试验机的测试工况，固定轴头高度，转速设置为60 r·min-1。利用柔性环模型计算RROC对稳态垂向接触力的影响，结果如图7（b）所示。

对比RROC测试数据及其对应的垂向接触力波动，可以看出虽然RROC的幅值波动仅为0.3 mm，但是稳态垂向接触力波动达到了79 N。这说明轮胎的均匀性参数在平顺性及动力学仿真中是一个需要考虑的重要因素。图7（b）可以体现出轮胎对RROC的垂向滤波特性，滤波作用包括弹性材料和几何结构（接地印痕长度）的影响。

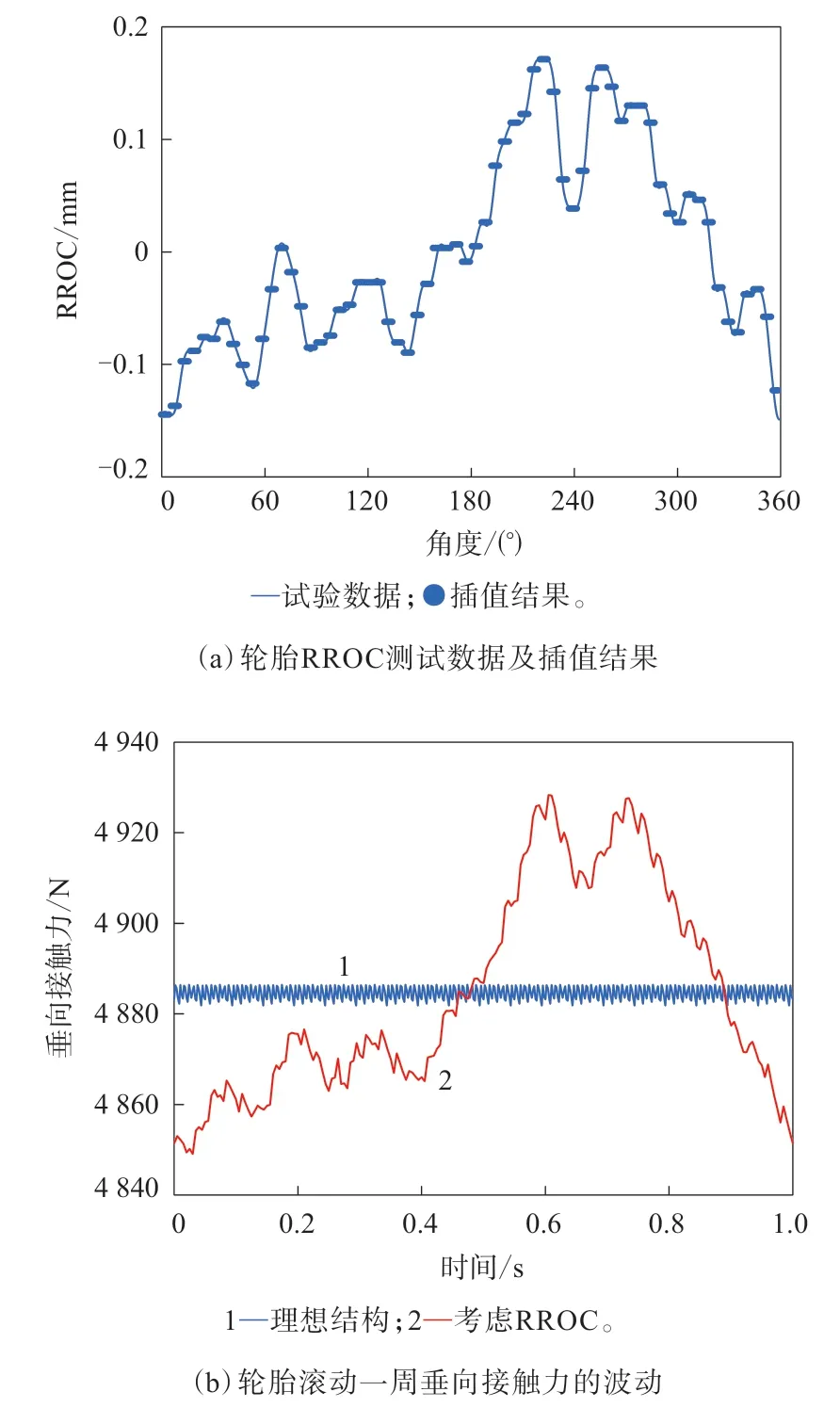
图7 由轮胎外表面中心点RROC引起的轮胎稳态垂向接触力波动

3.3 RROC导致的轴头RFV

利用刚柔耦合环模型，将RROC作为模型均匀性参数输入，低速均匀性试验机上实测得到的RFV与仿真结果的对比如图8所示，数据采集时间为1 s，即对应轮胎滚动一周。

图8 由RROC导致的RFV变化结果

从图8可以看出，在低速时，RROC是影响轴头RFV的主要因素。从仿真结果与试验数据的对比可以发现，刚柔耦合环模型可以很好地描述RFV的幅值及峰值位置，但是仿真结果仍存在一些误差。其中一个原因是本研究建立的刚柔耦合环模型仅考虑面内特性，因此无法考虑轮胎宽度方向上的尺寸不均匀，例如胎肩部位的尺寸波动和锥度效应等，而其仍会对RFV产生影响。另一个导致仿真误差的原因是模型中未考虑刚度不均匀所产生的影响，包括轮胎各部分结构搭接时产生的接头部位刚度分布不均及胎侧刚度分布不均等影响。

3.4 仿真结果的频域分析及验证

前面给出了RFV的时域分析结果，下面对RFV进行频域分析。由于试验台架的限制，测试数据进行了12阶滤波，因此在对仿真数据进行频域分析时，利用8阶低通Butterworth滤波器进行滤波，截止频率为12 Hz。图7给出的RROC对应的RFV的单边幅值谱的试验和仿真结果如图9所示，RFV的功率谱的试验和仿真结果如图10所示。

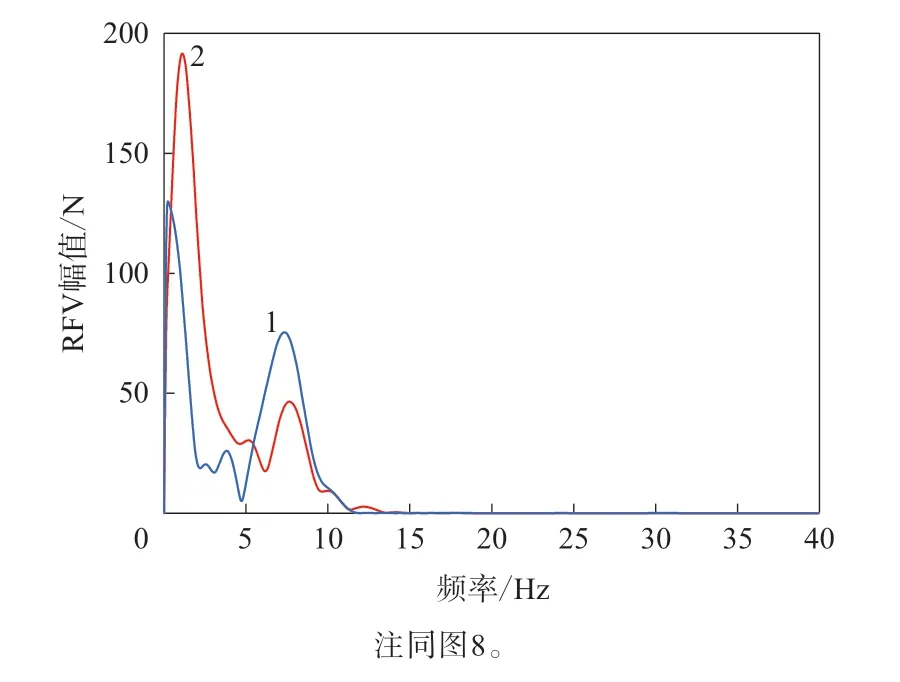
图9 RFV的单边幅值谱的试验和仿真结果

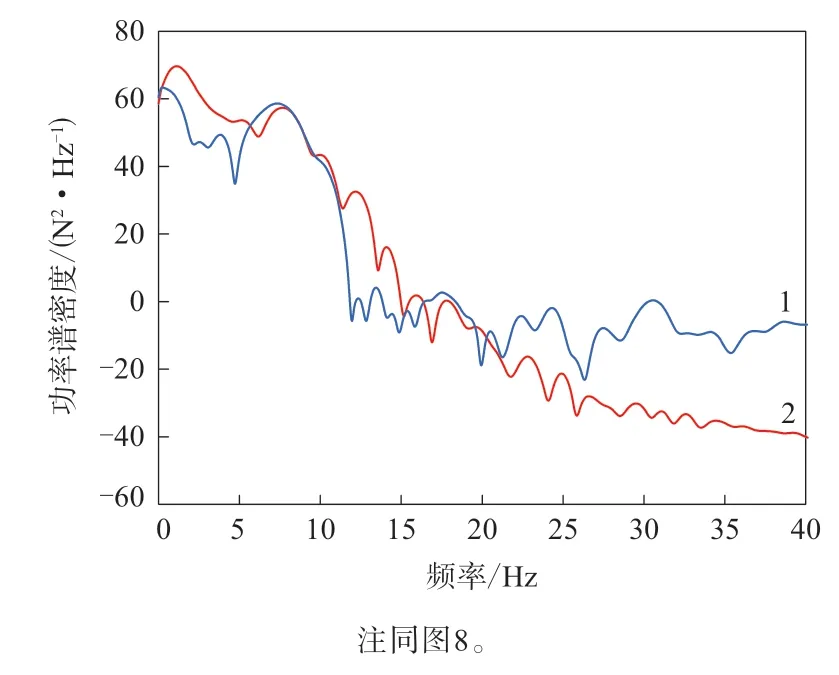
图10 RFV的功率谱的试验和仿真结果

从图9和10可以看出，本研究建立的仿真模型可以很好地反映出低速时由RROC导致的轴头径向力波动的频率信息。仿真结果能够准确预测单边幅值谱和功率谱的峰值位置，并且较为准确地预测各阶频率分量的大小。这说明基于刚柔耦合环模型预测由RROC导致的轴头径向力波动的方法具有较高的精度和可靠性。

4 结论

本研究建立了基于刚柔耦合环模型的完整轮胎均匀性理论模型，推导了柔性环模型的理论公式，得到了给定垂向负荷下柔性环的接触力分布算法，通过胎面胶厚度变化描述了轮胎RROC的影响，并通过引入刚性环和柔性环之间的耦合关系，建立了完整的刚柔耦合环模型仿真算法；进而给出了模型参数的辨识方法以及利用一组RROC及其对应RFV测试数据的参数优化算法，得到了模型参数的辨识结果；最后利用完整的模型参数进行低速均匀性仿真分析，并与台架试验数据进行时域和频域分析对比，验证了仿真结果与试验数据之间很好的一致性，进而证实了本研究建立的刚柔耦合环模型的准确性及可靠性。

本研究建立的轮胎刚柔耦合环模型不仅可以有效地建立轮胎结构、材料以及物理参数与轮胎均匀性之间的关系，同时也可以更普遍地应用于整车平顺性及动力学分析中。

对于低速时的RFV，其频率信息集中在低频段，轮胎表现出的特性类似于轮胎低速通过不平路面时的包容特性。在本研究中，这种对轴头力的扰动不再来源于不平路面，而是来自于轮胎结构本身的尺寸偏差，低速时并不会激发轮胎的一阶模态，即轮胎的整体运动。这也说明，仅利用低速下的均匀性数据无法实现对轮胎高速均匀性的预测，并且在高速时，质量不均匀的影响更加显著。因此，在对轮胎进行完整的均匀性分析时，需要在不同速度下进行测试。

致谢：本研究第二作者感谢中国留学基金委员会（CSC）的支持。