基于时间序列季节分类模型的轨道交通客流短期预测

唐继强，钟鑫伟，刘 健，李天瑞

(1.重庆市轨道交通(集团)有限公司，重庆 401120；2.重庆理工大学 计算机科学与工程学院，重庆 400054；3.西南交通大学 信息科学与技术学院，四川 成都 611756)

0 引 言

以轻轨和地铁为代表的轨道交通已经成为大城市重要交通方式；轨道客流预测对于轨道建设、交通运营和日常出行至关重要[1]。在城市交通资源日趋紧张、人们出行交通压力越来越大的情况下，轨道交通对优化土地资源利用、缓解城市交通拥堵提供了有效解决途径，成为城市交通现代化发展的重要手段。轨道交通具有准时、方便、快捷等特点，成为人们日常出行的首选。然而，随着城市规模增加、社会节奏加快、社会活动频繁，轨道交通也面临巨大挑战。如今的城市轨道交通呈现出总体客流暴增、客流分布不均衡等新特点，使得轨道交通运营和服务、人们出行时刻和线路选择变得越来越困难。为了提高运营效率、提升服务水平、引导人们舒适出行，需要准确预测客流，以便构建有效的应对策略。

客流预测是通过对历史客流数据分析和建模，对将来某时间段的客流进行估计，可划分为长期预测和短期预测。客流长期预测是通过分析城市土地资源利用、交通调查、人口出行统计等方式估计交通出行OD矩阵，典型的客流长期预测方法为四阶段法。四阶段法是将客流预测划分为交通生成、交通分布、交通方式划分和交通量分配这4个阶段。四阶段法主要用于交通规划和建设，主要预测城市区间长期的交通流量，对轨道交通运营和人们日常出行帮助不大。城市轨道交通是一种封闭交通，通过自动检售票系统(AFC)检票进出车站，并记录每次出行的时间和站点。AFC系统提供了精确的客流历史记录，目前大多数轨道交通预测均利用AFC数据进行客流预测。轨道交通预测关注的是以小时、天或周为单位的短期预测。短期预测可发现轨道交通出行模式和客流分布，对于优化车辆调度、引导人们出行具有重要意义。

轨道交通客流短期预测方法主要有线性预测方法、非线性预测方法和组合预测方法。轨道交通客流短期预测研究的核心是通过对AFC检票数据分析获得数据特征，建立数学模型对客流进行预测。线性预测方法是通过拟合线性客流预测模型，对客流进行预测，典型的线性预测方法包括时间序列分析方法、回归分析方法等；非线性预测方法是基于轨道交通客流的非线性特征，通过拟合非线性客流模型，对客流进行预测，典型的非线性方法包括人工神经网络预测方法、卡尔曼滤波方法、支持向量机方法等。一般而言，线性预测方法算法结构较简单，处理速度较快，但预测精度相对较低；非线性预测方法算法结构较复杂，预测精度相对较高，但处理速度较慢。为充分利用线性和非线性预测方法优点，学界提出了组合预测方法。组合预测方法是通过多种预测模型组合进行预测，典型的预测方法包括时间序列+人工神经网络、时间序列+小波分析、时间序列+支持向量机等方法。组合方法一般使用线性方法进行初步预测，再使用非线性预测方法改进预测方差，最终以获得预测速度和预测精度平衡。

上述方法中，时间序列客流预测是一种以统计理论为基础的线性预测方法[2]，该方法严谨、处理速度快、改进空间大，广泛用于轨道交通客流预测。滑动平均方法(MA)是最简单的时间预测方法，孟品超等[3]采用滑动平均法对轨道交通短期客流进行实时预测，发现该方法处理速度快。自回归滑动平均方法(ARMA)是时间序列的代表性方法，卢志义等[4]采用该方法对轨道交通短期客流进行了预测。自回归差分滑动平均方法(ARIMA)可处理不稳定的时间序列，李明敏等[5]对比了时间序列的滑动平均、ARIMA等方法，发现ARIMA模型预测效果最好。杨静等[6]在时间序列数据预处理阶段进行了改进，通过分析时间序列变点，找出分布较一致的时间序列进行预测。段金肖等[7]采用广义自回归条件异方差方法(GARCH)对轨道客流方差和波动性进行了研究，发现GARCH法不能有效提升预测精度，但是可减小预测置信区间。何九冉等[8]采用ARIMA-RBF组合法预测了短期客流，其主要工作是采用ARIMA法作基本预测，采用RBF神经网络对ARIMA法预测残差进行二次预测和改进。此外，李得伟等[9]采用ARIMA+小波神经网络组合方法对轨道交通的短期客流进行了预测。

通过对AFC检票时间序列数据分析，发现天气和气温等因素对客流不存在统计上的显著影响，但上下班、周末和节假日等社会活动对客流有显著影响。王夏秋等[10]针对AFC检票数据时间序列周期性特点，建立了以月为时间跨度的季节指数，对时间序列进行季节指数调整后，采用ARIMA法进行预测，显示出该方法良好的数据适应性。蔡昌俊等[11]、赵鹏等[12]、B.M.WILLIAMS等[13]、S.V.KUMAR等[14]分别采用ARIMA乘法季节模型对短期客流进行了预测，发现该方法具有很高的精度和良好的适应性。白丽[15]在ARIMA乘法季节模型基础上，针对节假日非常规客流，对客流建立虚拟变量，采用ARIMA和多元线性回归组合法进行了短期客流预测，其研究显示该法具有较强的适应性和较好的预测精度。

针对轨道交通客流周期性、季节性和社会活动随机性等特点，笔者提出采用时间序列季节分类模型进行短期客流预测。该预测方法在数据预处理阶段以天为时间单位，将AFC检票数据按照工作日、周末、节假日等进行分类，根据分类建立不同的ARIMA季节预测模板模型；在预测阶段，根据预测当天分类，选择对应预测模板进行客流预测。

1 时间序列乘法季节模型

时间序列乘法季节模型全称为乘法季节自回归差分滑动平均模型，其是在基本自回归差分滑动平均模型[16]基础上，引入乘法季节思想构建的时间序列模型[17]。

1.1 乘法季节自回归差分滑动平均模型

自回归差分滑动平均模型将数据模型表示为差分、自回归和滑动平均这3种成分[2]，乘法季节自回归差分滑动平均模型是在自回归差分滑动平均模型基础上，增加了拟合时间序列周期性相关关系的差分操作、自回归项和滑动平均项。该模型表示为ARIMA(p,d,q)(P,D,Q)s，如式(1)～(5)。

φ(B)Φ(B)(1-B)d(1-Bs)DYt=θ(B)Θ(B)et

(1)

φ(B)=1-φ1B-φ2B2-…-φpBp

(2)

θ(B)=1-θ1B-θ2B2-…-θqBq

(3)

Φ(B)=1-Φ1Bs-Φ2B2s-…-ΦPBPs

(4)

Θ(B)=1-Θ1Bs-Θ2B2s-…-ΘqBQs

(5)

式中：p、d、q分别为自回归阶数、差分阶数、滑动平均阶数；B为延迟算子；φ(B)、θ(B)分别为自回归项、滑动平均项的时间滞后；P、D、Q分别为拟合周期性关系的自回归项的阶数、差分操作阶数、滑动平均项的阶数；S为季节周期；Φ(B)、Θ(B)分别为自回归项、滑动平均项的季节性滞后。

1.2 建模过程

乘法季节自回归差分滑动平均模型建模过程如图1，该过程包含模型识别、参数估计和模型诊断这3个阶段。模型识别阶段采用平稳性检验和相关性检验识别模型系数，平稳性检验用于识别阶数d和D，相关性检验用于识别p、q、P和Q。识别模型系数后，在模型参数估计阶段采用回归分析方法，以确定线性组合参数φ(B)、Φ(B)、θ(B)和Θ(B)。模型诊断阶段对模型残差进行相关性检验，确定残差不存在相关性，若未通过检验则需回到模式识别阶段重新建模，通过残差相关性检验模型就可用于预测。

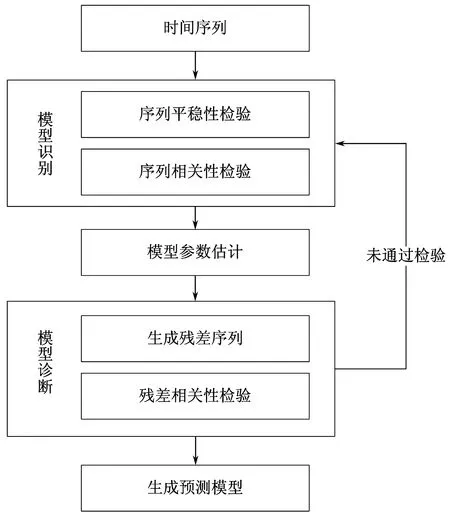
图1 乘法季节自回归差分滑动平均模型建模过程

2 时间序列模型改进

笔者以重庆轨道交通6号线茶园站(编号0601)在2018年9月共计30 d的AFC检票数据为例，建立时间序列季节分类模型，对该站点2018年10月的客流进行预测。

2.1 轨道交通客流特征分析

为了对轨道交通客流特征有更加直观认识，笔者选择该站点2018年9月共计30 d的AFC检票数据进行分析。轨道运营时间为06:00—23:15。设置数据统计时间间隔为15 min，每天分别生成69个进站数据和出站数据，30 d共计2 070个进站数据和出站数据。图2分别为该站点进站和出站的客流时间序列。

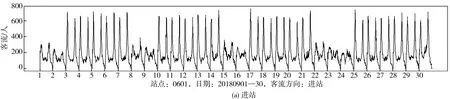
图2 茶园站点进出站客流季节性特征

从图2可看出：进站与出站的客流模式基本一致，具有较突出的季节特征：① 进出站客流都表现出以“天”为时间单位的周期性；② 进出站每个周期的客流都表现出早晚高峰；③ 9月1、2、8、9、22、23、24日这几天进出站客流波形呈现出较小的早晚高峰，其他日期进出站客流波形呈现出较大的早晚高峰；④ 出站较进站平峰客流有较大波动性。

从时间上看，9月1、2、8、9、22、23日为周末，9月24日为中秋节，而其他时间为工作日。这些季节性特征不仅仅是该站点的独有特征，对其他站点客流数据分析也具有相似特征。

2.2 时间序列季节分类模型

针对轨道客流特征和模式，笔者提出使用工作日、周末、节假日等日历模板分别建立分类预测模型。日历模板包括：星期一、星期二、星期三、星期四、星期五、星期六、星期天、元旦节、春节、清明节、劳动节、端午节、中秋节、国庆节等。对于有多天的节日，可细分为节日第1、2、3天等；对于周末调休，将该日调整为对应的工作日；对于智博会、大型展览等重大社会事件，可建立对应的分类。表1为2018年9月的日历模板。图3为时间序列季节特征分类预测模型建立过程。

表1 2018年9月季节模板

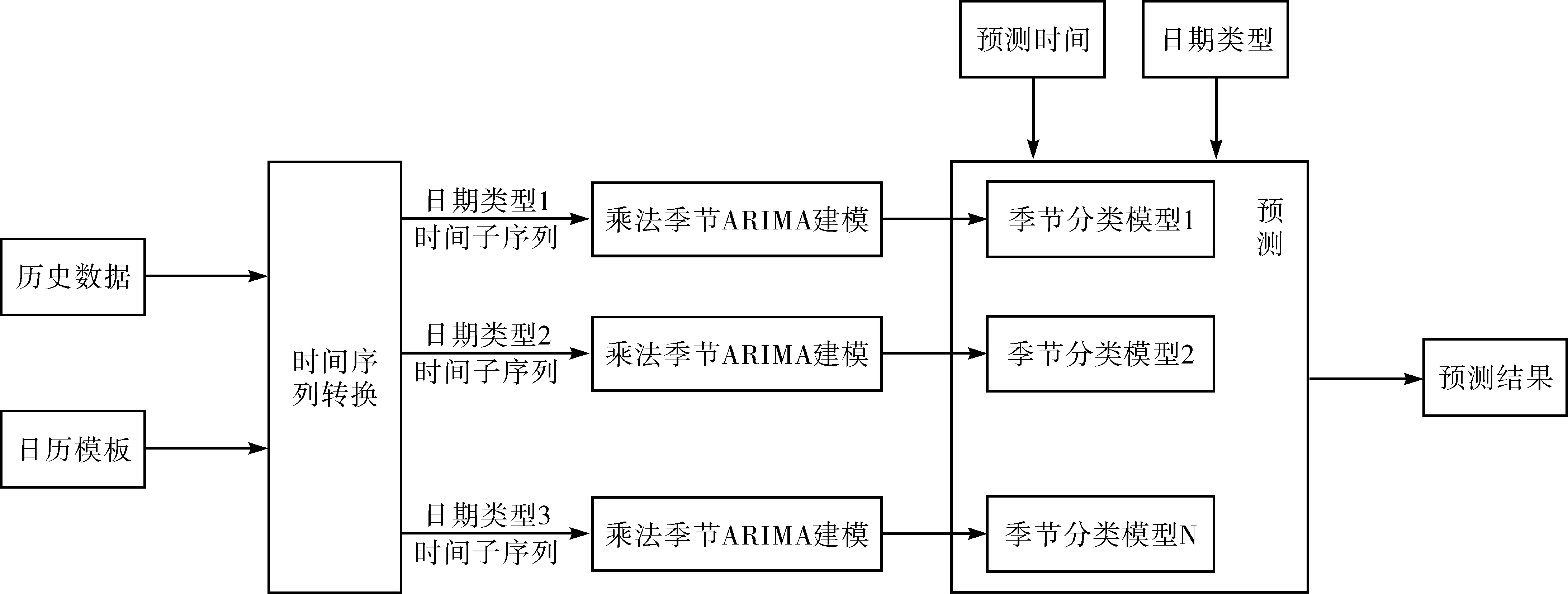
图3 时间序列的季节特征分类预测模型

3 季节分类建模实例

3.1 子序列季节分类模型建模

以星期五日期类型为例，具体说明模型识别和参数估计过程。星期五类型包含9月7、14、21、28、30日共5个周期数据，如图4。

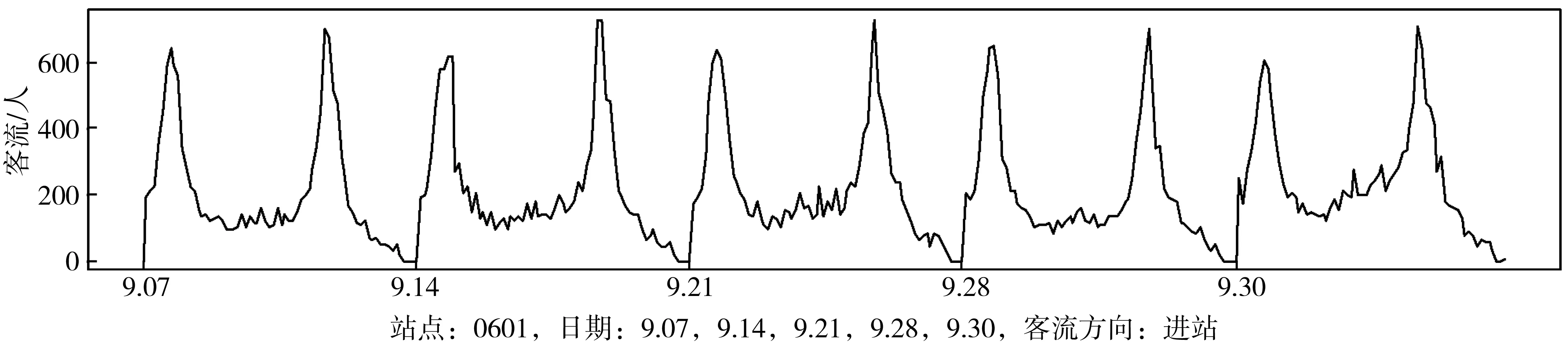
图4 2018年9月星期五日期类型进站子时间序列

检验时间序列平稳性，以推断序列的差分阶数d、季节差分阶数D。笔者采用Kass法进行检验，测试函数是R语言库的ndiffs函数，对星期五日期类型的时间序列进行循环检查，直到原始序列和季节调整序列均平稳，最后确定差分系数d=1、D=1。对星期五日期类型序列进行d=1、D=1的差分计算，其结果如图5。

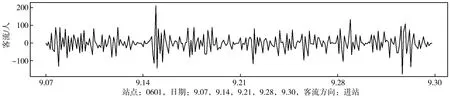
图5 2018年9月星期五日期类型进站差分序列(d=1、D=1)

检验时间序列相关性，以识别序列的自回归阶数p、移动平均阶数q、季节回归阶数P和季节移动平均阶数Q。笔者选择AIC作为模型选择标准。识别模型阶数的过程为：通过acf自相关函数确定移动平均阶数，pacf偏自相关函数确定自回归阶数，eacf扩展自相关函数确定自回归和移动平均项的阶数。在实际搜索建模过程中，R语言库的auto.arima函数有助于提供初步选择[18]，该函数给出模型ARIMA(2,1,2)(0,1,0)69，其AIC=2 760.72。绘制该序列的acf自相关函数，如图6(a)。图6(a)中：1～2阶滞后和69～70阶滞后相关性显著，故可考虑模型ARIMA(0,1,2)(0,1,1)69，其AIC=2 690.58。绘制该序列的pacf偏自相关函数，如图6(b)。图6(b)中：1～5阶滞后和69阶滞后偏自相关性显著，故可考虑ARIMA(5,1,0)(1,1,0)69，其AIC=2 710.37。通过计算eacf扩展自相关矩阵，发现非季节部分选择p=2、q=5，季节部分选择P=1、Q=1较好，获得备选模型ARIMA(2,1,5)(1,1,1)69，其AIC=2687.34。根据AIC准则，预测模型ARIMA(0,1,2)(0,1,1)69和ARIMA(2,1,5)(1,1,1)69的AIC较小，但从模型简洁性和计算性能等方面考虑，更倾向于选择模型为ARIMA(0,1,2)(0,1,1)69。

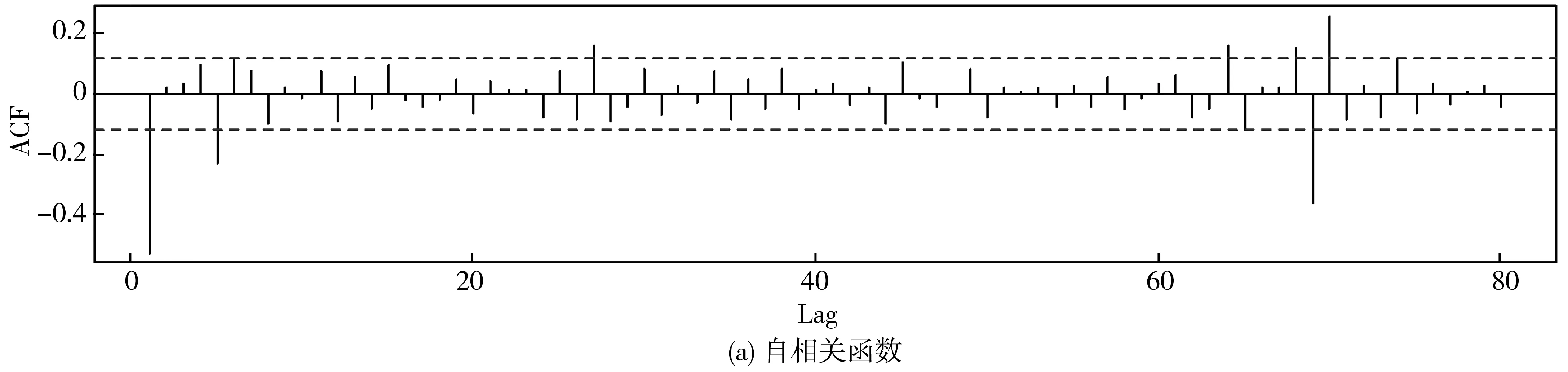
图6 2018年9月星期五日期类型进站差分平稳序列的自相关函数和偏自相关函数

对识别模型的自回归参数φ(B)、Φ(B)和移动平均参数θ(B)、Θ(B)进行估计。模型ARIMA(0,1,2)(0,1,1)69的线性回归参数的极大似然估计如表2。通过代入估计参数，建立该模型的表达，如式(7)。计算该模型理论自相关函数，如图7。

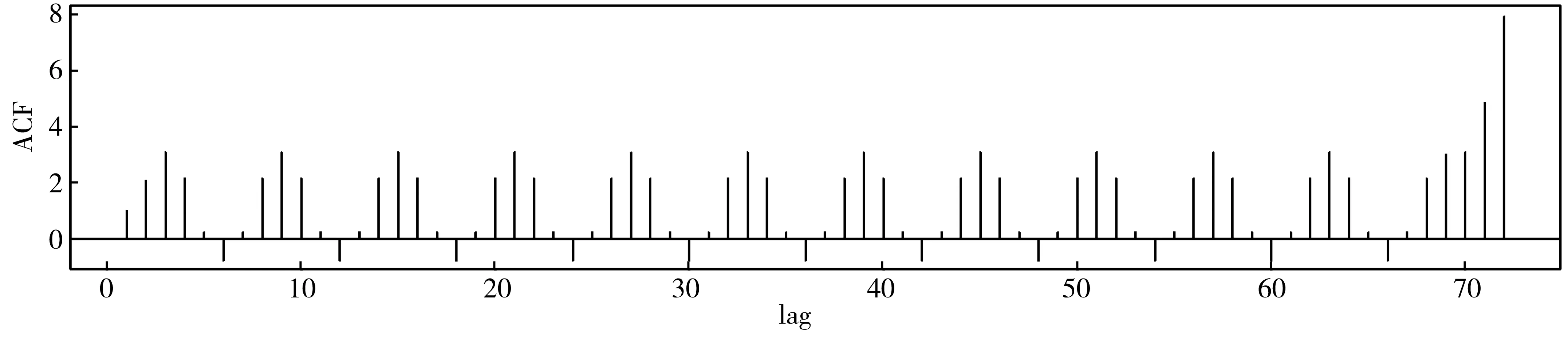
图7 模型ARIMA(0, 1, 2)(0, 1, 1)69自相关函数

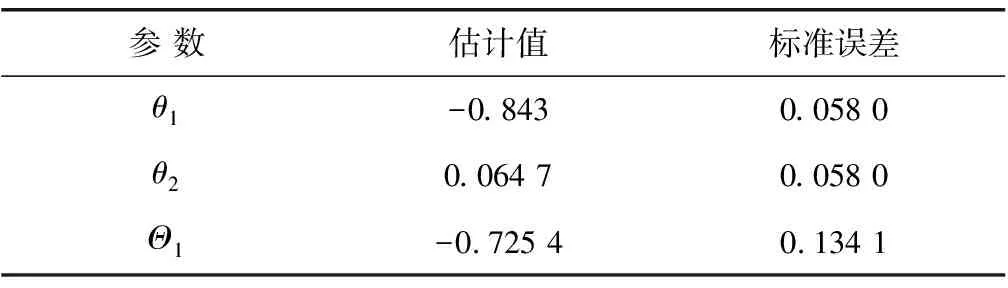
表2 模型ARIMA(0, 1, 2)(0, 1, 1)69的参数估计

Yt=Yt-1+Yt-69+Yt-70+et+0.843et-1-0.0647et-2+0.725 4et-69+0.611 5et-70-0.046 9et-71

(7)

通过残差分析对模型进行诊断。图8为ARIMA(0,1,2)(0,1,1)69模型的残差图。模型残差已是随机噪声，由于9月30日为国庆调休，故残差波动性较大。采用Box-Ljung检验对残差进行检验，设置滞后为138(周期的2倍)，得到pvalue=0.853 5，表明该模型已捕获时间序列的依赖关系。使用以上方法对该站点其他日期类型建立特征模板模型，如表3。

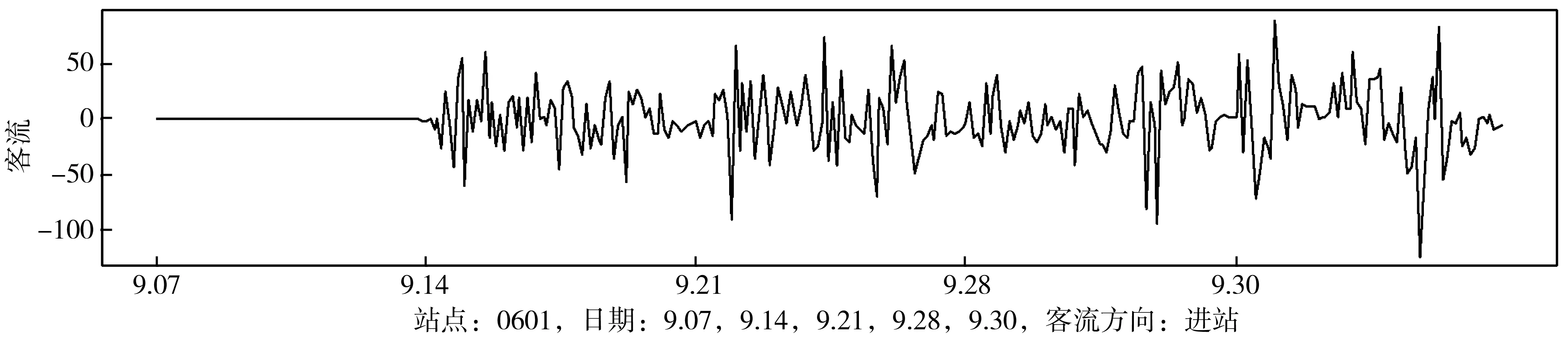
图8 模型ARIMA(0,1,2)(0,1,1)69残差

表3 2018年9月茶园站的时间序列季节特征模型

3.2 模型应用性分析

笔者设计了3组实验对2018年10月第2周的客流进行预测，以此来说明季节分类模型有效性。

3.2.1 实验1

采用星期五模型预测10月12日的客流，预测值与实际值对比情况如图9(a)，客流预测残差如图9(b)。图9(a)中：星期五模型预测值紧密贴合实际值；图9(b)中：预测残差围绕均值(大约等于0)上下波动，该残差图平均绝对误差为26，亦即每15 min的客流预测，平均存在26人误差。由图12也可看出：最大误差为每天开始的两个数据，故在对数据预处理过程中，忽略序列的前后2个数据点，对建模和预测更为有利。星期五模型较好地预测了星期五的客流。

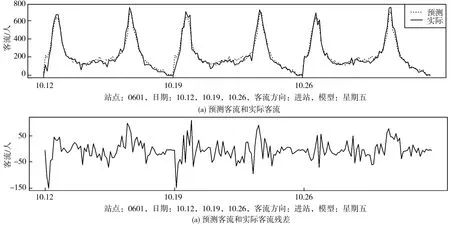
图9 2018年10月茶园站星期五日期类型的预测客流与实际客流及残差

3.2.2 实验2

采用星期六模型预测10月12日的客流，预测值与实际值对比情况如图10(a)，客流预测残差如图10(b)。在图10(a)中：预测值曲线很好地体现出了星期六数据特征，但无法贴合实际数据曲线；在图10(b)中，预测残差存在诸多高峰，星期六模型无法拟合这些特征，该残差图的平均绝对误差为74。星期六模型虽拟合了星期六的平坦曲线季节特征，但无法有效预测星期五客流。

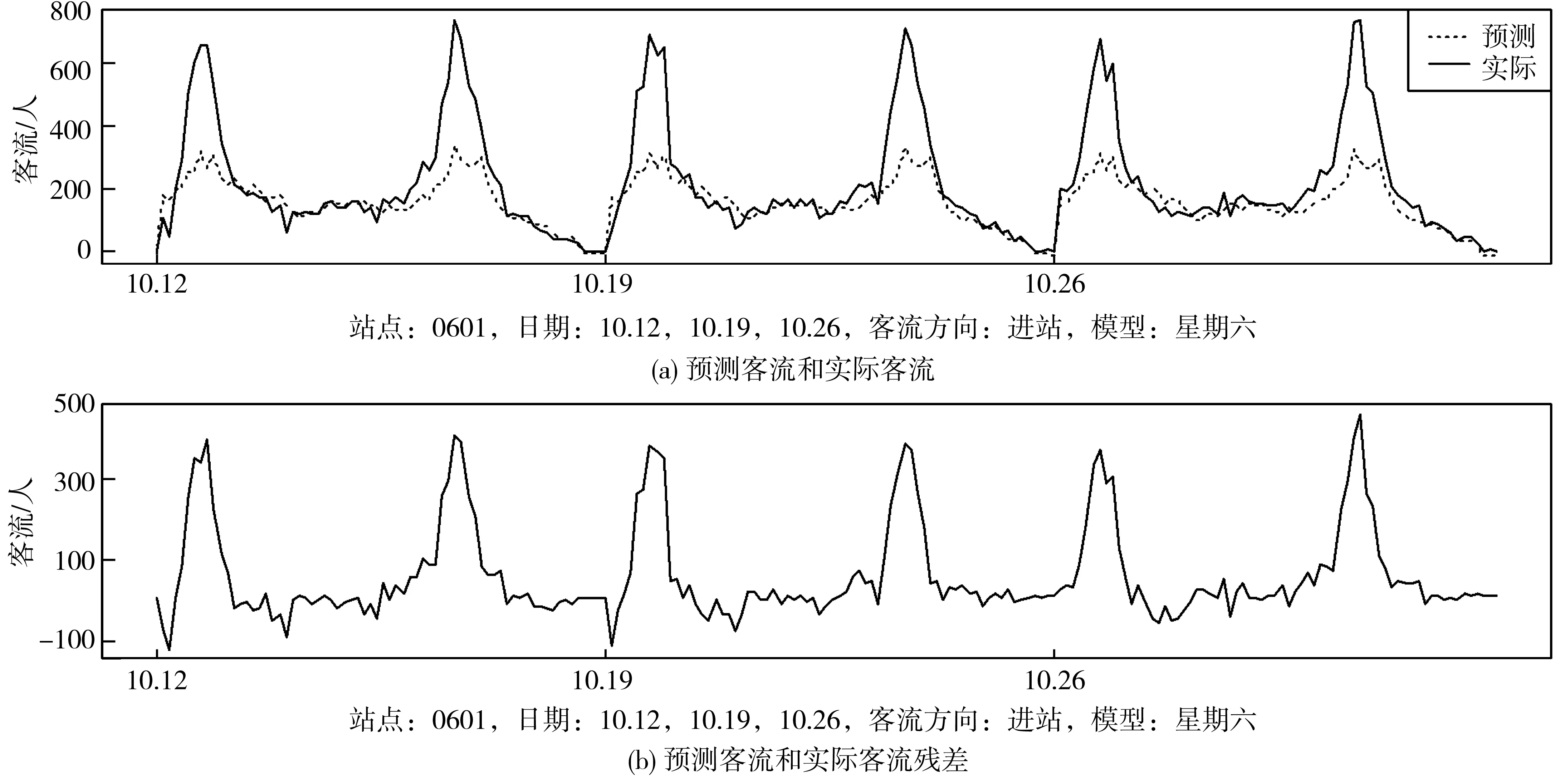
图10 2018年10月茶园站星期六日期类型的预测客流与实际客流及残差

实验1、2表明：星期五模型能很好预测星期五客流，而星期六模型无法有效预测星期五客流。进一步检查其他模型对星期五的预测情况发现：星期一至星期五模型能有效预测10月12日客流，而星期六和星期天模型无法有效预测10月12日客流。回顾图2，星期一至星期五曲线基本属于同一种季节性特征，而星期六和星期天曲线属于另一种季节特征。故星期一至星期五模型能较好预测星期一至星期五客流，星期六和星期天模型能较好预测星期六和星期天模型。根据两组实验，在预测要求不高情况下，可划分为周日和周末两个特征模板，以减少模型数量。

3.2.3 实验3

实验3是采用连续通用模型和上述季节分类模型预测10月8—14日客流。图11显示了两种预测方式的平均绝对误差。连续性通用乘法季节自回归差分滑动平均模型的建立方法为：采用9月1日—10月7日真实数据建立10月8日连续预测模型；采用9月1日—10月8日真实数据建立10月9日连续预测模型；以此类推，为10月8—14日每天建立一个连续预测模型。季节分类预测方法为：采用星期一模型预测10月8日(星期一)客流，采用星期二模型预测10月9日(星期二)客流；以此类推，最终预测10月8—14日每天客流。图11中：方块点划线和圆点划线分别表示每天连续预测和季节分类模型的平均绝对误差。

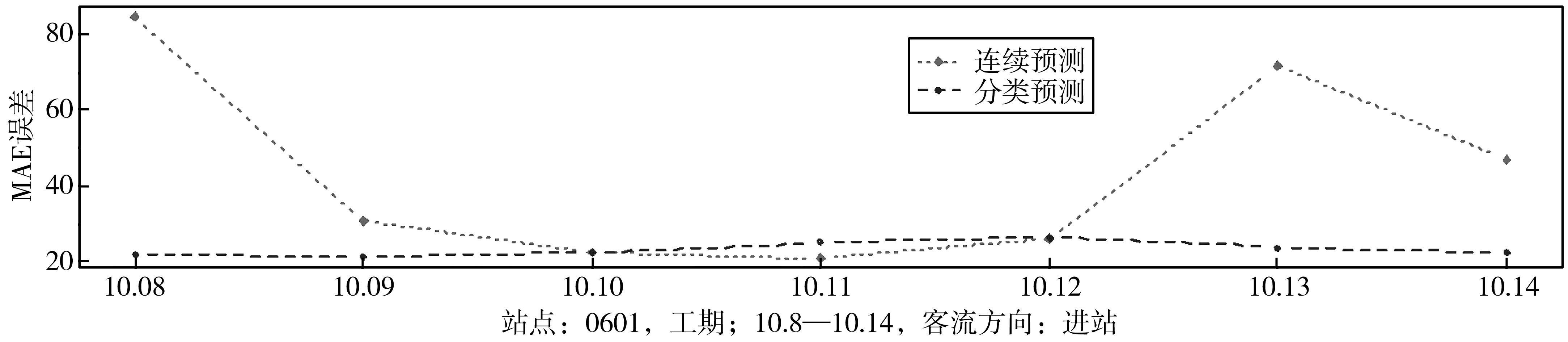
图11 2018年10月第二周分类预测与连续预测平均绝对误差对比

从图11可看出：连续预测平均绝对误差波动显著，在10月8—9日(星期一、二)和10月13—14日(星期六、星期天)波动达最大值，而季节分类模型平均绝对误差较低且无波动。回顾图2，星期一至星期五曲线基本属于同一种季节性特征，而星期六和星期天曲线属于另一种季节特征，在季节特征交界处，连续客流预测以最近特征推断将来特征，导致了巨大的误差和误差波动；而季节分类模型不存在特征过渡，也就不会产生误差波动。

连续预测和季节分类模型在10月10—12日误差对比不显著，连续预测有可能比季节分类模型预测更好。出现这种情况主要原因为：10月8—12日基本属于同一种季节性特征，连续预测恰好利用了10月8—9日的相似客流，对10月10—12日客流进行了合理推断。基于这一特点，季节分类模型可利用当天采集的客流数据建立更加精准的客流模型来推断未来部分时间客流。例如：假设10月12日已经获得当天06:00—11:00点的24个数据，可将9月星期五数据和这24个数据构成星期五子序列，实时重构星期五季节分类模型，通过实时模型来预测10月12日接下来时间段客流。

4 结 论

针对轨道交通客流强烈的季节性特征，笔者提出基于时间序列季节分类模型的短期客流预测方法。将预测时间以天为单位建立日历模板，采用乘法季节自回归差分滑动平均方法建立各个模板的季节分类模型，根据预测时间匹配的季节模型进行短期客流预测。

以重庆轨道交通6号线2018年9月的完整客流数据为例，建立了日历模板和季节分类模型，并对2018年10月第2周客流进行了预测。笔者设计了3组实验，在第1、2组实验中，星期五模型预测星期五客流误差为26人，而星期六模型预测星期五客流误差为74人，表明预测算法和数据特征对客流预测都有较大影响，而数据特征影响更为明显；在第3组实验中，连续预测误差为21～84人，季节分类模型误差为21～24人，表明季节性分类模型能有效预测客流，误差较小，避免了误差波动性问题。