基于可靠锚节点和粒子群优化的DV⁃Hop 算法
2021-07-18李同锋杜秀娟
李同锋,杜秀娟,谢 平,杨 帆
(青海师范大学 计算机学院,青海 西宁 810000)
0 引言
无线传感器定位算法通常分为基于测距算法(Range⁃based Algorithm)和无需测距算法(Range⁃free Algorithm)两类[1⁃3]。无需测距算法DV⁃Hop 因其实现成本低、算法简单等优点得到了广泛应用,是当今研究的热点之一[4]。近年来,国内外诸多学者[5⁃9]针对DV⁃Hop算法的不足之处进行了改进,效果明显。本文针对DV⁃Hop 算法的不足之处进行了改进,仿真结果表明效果明显。
1 DV⁃Hop 算法原理及误差分析
DV⁃Hop 算法定位过程包括以下阶段[9⁃10]。
1.1 泛 洪
锚节点首先向邻居节点广播包含自身位置、ID 号和跳数值为0 的信息,邻居节点第一次收到该信息后,保留该信息,并将跳数加1 发送到它的邻居节点。对于收到同一个锚节点发来的信息,以最小原则更新本地跳数值。该阶段完成后,监测区域中所有节点都已知道锚节点的位置坐标及到锚节点的最小跳数。
1.2 计算锚节点平均跳距
每一个锚节点通过式(1)计算自身的平均跳距。

式中:(xi,yi)表示锚节点i的坐标;hopsij为锚节点i和j之间的最小跳数。计算完成后向网络广播它们的HopSize。
1.3 计算未知节点坐标
未知节点采用距离本身最近的锚节点的平均跳距作为自己的平均跳距。未知节点k到锚节点i的估算距离记为dik:

式中:HopSizei代表距离k节点最近的锚节点平均跳距;hopik为锚节点i到未知节点k的最小跳数。根据式(2)和基本定位法进行定位,用方程组表示为:
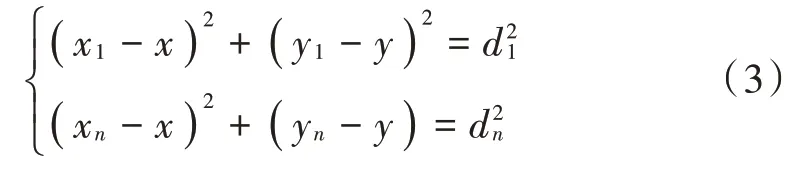
把式(3)写成AX=B的形式,A,B和X的具体值如下:

解之可得:
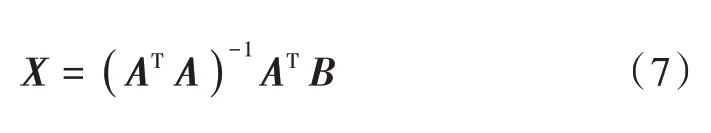
1.4 误差分析
1)曲线代直线和通信范围内节点跳数均视为1 跳。在传统DV⁃Hop 算法中,锚节点的平均跳距是根据锚节点之间的实际距离与两者之间跳数的比值求得,监测区域中的锚节点是随机分布的,路径不可能都是直线,锚节点之间的跳数越多,计算得到的平均跳距误差越大。
在计算跳数时,通信范围内的跳数均视为1 跳。锚节点B和C都在锚节点A的通信范围内,传统DV⁃Hop算法都按照1 跳距离计算A与B,A与C之间的跳数。但实际上锚节点B和C到锚节点A的跳数存在误差,如图1所示。
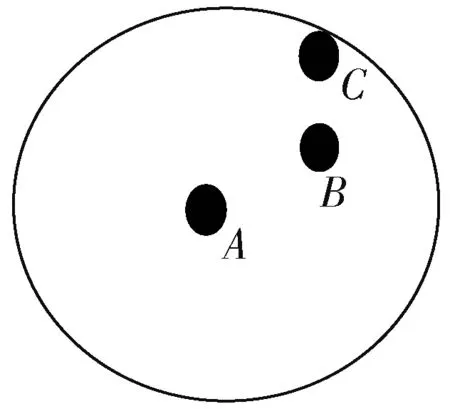
图1 一跳距离示意图
2)未知节点仅仅采用单一锚节点的平均跳距。在传统DV⁃Hop 算法里,未知节点采用距离自身最近的锚节点的跳距作为平均跳距,求得两者之间的距离,但是监测区域里的节点是随机分布的,距离未知节点最近的锚节点不能反映其他锚节点的分布情况。
2 改进的DV⁃Hop 算法
2.1 可信锚节点选择和跳数修正
针对1.4 节1)中误差的原因,在计算锚节点平均跳距时选用可信度较高的锚节点,即选用共线度较高的锚节点。

式中:δ为理想平均跳距;dij为锚节点之间的实际距离;R为节点的通信半径。锚节点计算自身平均跳数,如大于δ,则认为在该路径上锚节点之间的共线度较低,即可信度较低,如用来参与计算锚节点的平均跳距,会引起较大误差,故删除该锚节点。
采用文献[11]中的方法对跳数进行修正,分别引入最优跳数值(hij)、实际偏差值(εij)和跳数因子(fij)修正跳数,具体定义如下:

修正后,锚节点间的跳数计算公式为:

因此,求解锚节点的平均跳距改为:
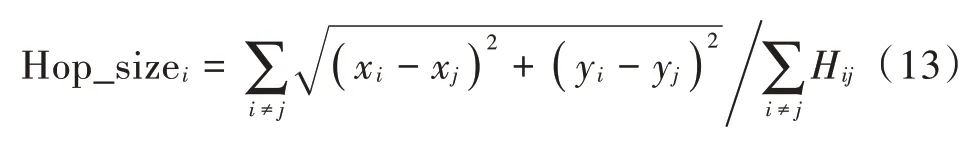
2.2 未知节点平均跳距的修正
针对1.4 节2)中存在的问题,区别于传统DV⁃Hop算法,采用满足定位条件的锚节点的平均跳距误差为权重,综合求得未知节点的平均跳距。

式中errorij为锚节点i和锚节点j之间的距离误差。平均距离误差为:
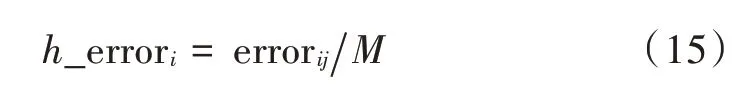
式中:h_errori为锚节点i的平均距离误差;M为锚节点i周围锚节点的数目。
锚节点i的权重为:

结合式(16),未知节点k的平均跳距为:

2.3 采用粒子群算法优化未知节点位置
2.3.1 粒子群算法原理
粒子群优化算法[11⁃13]是一种基于群体智能理论的模拟技术,其基本原理是:每个粒子视为可行解空间中的一个解,粒子具有初始位置和初始速度,粒子自由运动,通过式(18)和式(19)不断更新自身速度和位置,直到迭代次数大于最大迭代次数或满足一定误差范围,算法停止,从而得到最优解。

式中:Vij(t+1)为粒子的速度,i为粒子个数,j为维数;ω为惯性权重;t为迭代次数;c1和c2分别表示自身学习能力和全局学习能力;γ1和γ2为[0,1]之间的随机数。
2.3.2 算法实现步骤
1)初始化粒子速度、位置和数目,算法在初始阶段,粒子的初始位置就是全局最优位置。
2)计算每个粒子的适应度函数:

3)粒子与适应度函数作比较,并通过式(18)和式(19)更新自身速度和位置。
4)当达到最大迭代次数后,算法结束。
3 实验结果与分析
采用Matlab R2015b 仿真平台对本文改进的算法进行仿真,并与传统DV⁃Hop 算法和DV⁃Hop+PSO 算法进行对比。实验环境设置如下:仿真区域大小为100 m×100 m,随机放置100 个传感节点,其中锚节点的比例为8%,传感节点的通信半径为R=30 m。采用节点平均定位误差errorave作为本次算法结果的评价标准。

网络节点随机分布如图2 所示,其中网络节点总数为100,锚节点数为8。
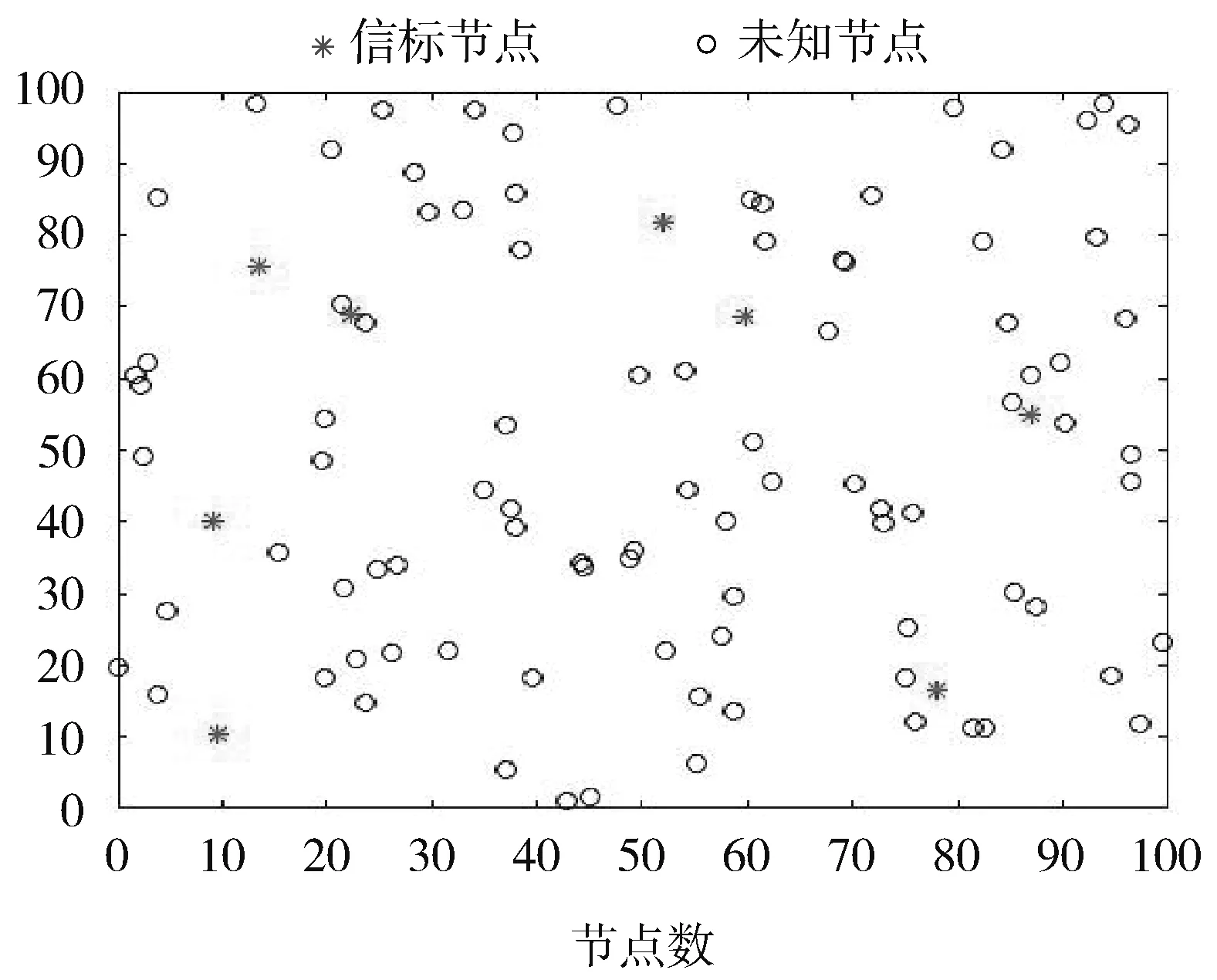
图2 网络节点随机分布图
图3 表示锚节点数为8,节点传输半径为30 m 时,本文改进的DV⁃Hop 算法、传统DV⁃Hop 算法和DV⁃Hop+PSO 算法的节点定位误差,从图3 中仿真结果看出,本文改进的算法定位误差相对较低。

图3 仿真结果对比
1)不同锚节点数对定位的影响
图4 表示锚节点数对节点平均定位误差的影响,设置节点总数为100,节点传输半径为30 m,锚节点数依次取10,15,20,25,30 时对平均定位误差的影响。从仿真结果图中可以看出,随着锚节点数量的增加,节点的平均定位误差在减小,定位精度在提高,说明增加锚节点数量,能够提高定位精度,也揭示了该算法依赖锚节点进行定位的本质。

图4 锚节点数对定位的影响
2)不同通信半径对定位的影响
图5 表示在节点总数为100,锚节点数为10 时,通信半径大小对节点定位的影响。从仿真结果看出,随着节点通信半径的增加,平均定位误差在逐步减少,定位精度在提高。说明通信半径影响着节点之间的跳数,如果通信半径设置的过小,导致很多节点之间无法通信,进而无法完成定位工作;反之,则导致定位误差增大。

图5 通信半径对定位的影响
4 结语
针对传统DV⁃Hop 算法的不足,本文提出了一种改进的DV⁃Hop 算法,通过仿真结果看出,改进的算法在定位精度上优于传统DV⁃Hop 算法和DV⁃Hop+PSO 算法。但在网络开销、PSO优化上还存在不足,这也是后期研究的方向。
