基于蝙蝠优化器的三维无线传感器网络节能覆盖增强策略*

庄海燕

(铁道警察学院图像与网络侦查系，河南 郑州450002)

众所周知，在物联网(IoT)中，计算机能够在没有人类交互的情况下，自动访问对象和环境的相关数据信息。其中，无线传感器网络(WSNs)则是实现物联网传感器节点感知的关键推动因素，为物联网带来更加丰富的感知和驱动能力[1]。作为物联网的关键场景之一，无线传感器网络会根据目标的有效覆盖效果执行任务[2]。目前，无线传感器网络在战术监视、地震监测、辅助导航、污染监测等领域得到广泛应用，并因其在物联网中的关键作用而逐渐成为物联网研究的热点之一[3]。

对目标的有效监测是三维无线传感器网络任务执行的基础[4]。其中，确保目标区域能够被传感器节点有效覆盖是提高三维无线传感器网络监控质量和网络可靠性的关键[5－6]。但是三维无线传感器网络布局受环境影响较大，尤其在恶劣、偏远的地区，由于人为干预较少，使得网络无法对传感器节点的电池进行充电或更换，从而降低三维无线传感器网络寿命，导致无法持续、可靠的完成目标任务[7－8]。因此研究如何提高三维无线传感器网络节点的有效能耗，可以有效延长传感器网络寿命，从而提高三维无线传感器网络监控覆盖率。通常，在三维无线传感器网络的重新部署中，会产生大量的传感器节点移动和信号传输出，使得三维无线传感器网络产生大量的能量消耗，导致网络监控质量和网络可靠性不佳[9]。因此如何减少三维无线传感器网络的移动总能量消耗和平衡节点剩余能量是当前三维无线传感器网络重新部署策略中亟待解决的关键问题[10]。

针对上述问题，国内外众多专家学者开展了大量研究。文献[11]提出了一种基于协同进化粒子群算法的无线传感器网络节能优化覆盖算法，通过优化无线传感器网络覆盖率、剩余能量和冗余程度，构建粒子群优化模型，运用遗传算法交叉变异算子提高算法寻优能力，延长了网络生命周期，并获得良好的覆盖率。文献[12]提出了一种基于遗传PSO的无线传感网络覆盖优化算法，通过运用具有自适应交叉变异因子的遗传算法搜索解空间，增强PSO粒子群全局搜索能力和搜索范围，强化算法寻优能力，从而提高节点的覆盖率。但上述研究成果在无线传感器网络随机部署移动节点时，存在节点分布不均匀的问题，从而导致网络覆盖率较低。文献[13]提出一种基于节点调度和路由协议优化算法，通过选择冗余睡眠节点来替换死节点延长网络寿命，并通过优化汇聚节点周围传感器的数据通信方式，构建不均匀的群集以平衡能量负载，从而减少冗余传感器节点的数量，并提高数据传输的能量效率。文献[14]提出了一种基于博弈论的节点功率控制算法，运用剩余能量、发射功率等要素构建功能函数，并将剩余能量作为下一跳节点，运用功率博弈算法不断调整修正，从而控制节点传输功率，降低网络节点传输能耗。文献[15]提出了一种改进的Bkd-Tree启发式节能群集算法，通过集群策略处理与数据流量相关的节能问题，可在最小化能量、延迟和抖动的情况下提高网络节点吞吐量，从而有效降低能耗10%以上，使无线传感器网络具有更佳的性能。但上述研究中，无线传感器网络覆盖存在收敛速度慢、易早熟等问题，且网络覆盖率较低、部署成本高。

针对上述研究存在的相关问题，本文提出了一种基于蝙蝠优化器的三维无线传感器网络节能覆盖增强策略。首先，通过截角八面体将覆盖增强和能量优化问题转化为将节点移动到截角八面体的任务分配问题；运用蝙蝠优化器实现无线传感器网络的最小化总能耗和平衡剩余能量的多目标优化。最后，通仿真对比分析验证所提策略的有效性与可靠性。

1 问题阐述

通常，三维监控区域由包含K个网格的三维空间表示。其中，每个传感器在三维空间中都有一个球形范围，球心代表传感器节点，半径代表节点感应范围。对于具有K个网格的三维空间Ω，当满足条件d i，j≤K时，S i可以检测到G j。其中，S i是第i个具有坐标(x si，y s i，z s i)的传感器节点，G j是坐标为(x g j，y gj，z gj)的第j个网格的质心，R为传感器节点的感知半径，d i，j为S i与G j之间的欧式距离。

由于三维无线传感器网络覆盖控制的主要研究内容是利用最少的节点来增强网络覆盖效果，因此假设传感器节点能够获取其位置信息，所有传感器节点具有相同的感知半径，且暂时忽略由于环境的复杂性导致的声通道路径损耗、端间延迟和数据包丢失率。如果最终达到完全覆盖效果，则将该策略定义为最有效的覆盖增强策略，如图1所示为截角八面体的切割过程。

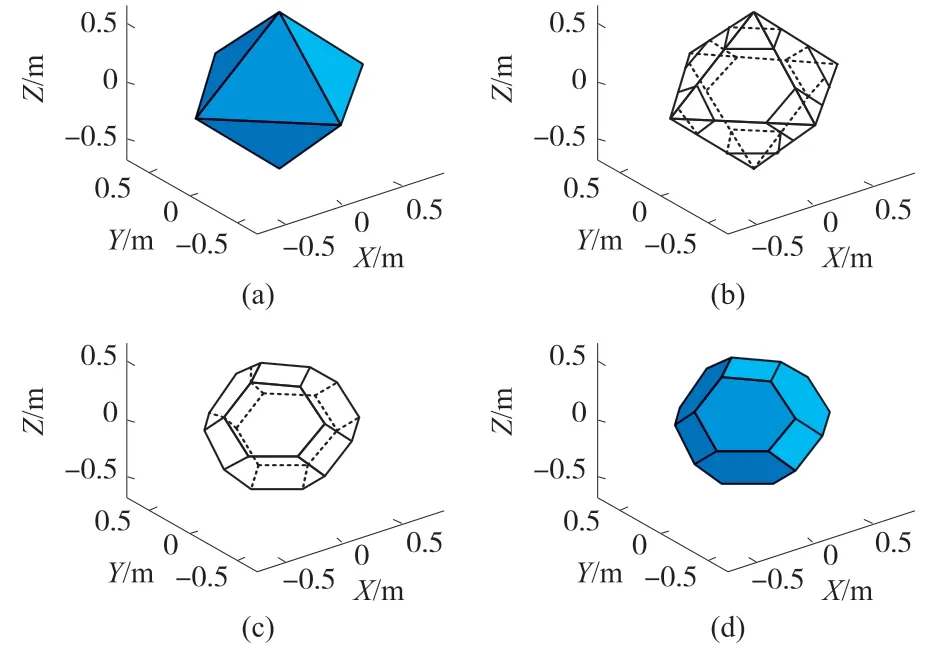
图1 截角八面体切割过程

如图2所示，为截角八面体的堆叠间隔图，其中的箭头表示传感器节点的感知半径，即为截角八面体的外接球体半径。根据图1所示切割过程的几何关系，其堆叠间隔是长度的两倍。

图2 截角八面体的堆叠间隔

因此，可根据位置关系将用于无缝堆叠Ω的所有截角八面体分为两类。其中，假设Ω的长、宽、高分别为L1、L2和L3，并令δ＝4 5R/5为堆叠间隔，质心分别为(0，0，0)和(2 5R/5，2 5R/5，2 5R/5)，可将第一类截角八面体的质心坐标表示为式(1)所示:

因此，无缝地堆叠Ω所需的最小截角八面体数可以通过式(3)计算:

其堆叠效果如图3所示，使用外球面半径为R的截角八面体无缝地堆叠Ω后，将节点移动到截角八面体的质心，可最大程度地提高最终覆盖率，并使节点数量最小化。但是要提高节点覆盖率仍需要解决以下三方面问题。

图3 堆叠效应

①移动能耗模型

剩余能量E i，j的数学表达如式(4)所示:

式中:E o i为S i的初始能量；e为S i移动1ft时的能量消耗；d i，j为S i与G j之间的欧几里德距离。其中，节点剩余能量的均匀性如式(5)所示:

式中:N为节点数；E i，j为移动到G j后S i的剩余能量。通常，无线传感器网络的生命周期由最先衰亡的节点生命周期表示，因此重新部署过程中，能量优化的关键是降低网络总移动能耗，平衡节点的剩余能量。

②能量消耗优化

将重新部署问题转换为任务分配问题，当其满足式(3)中所述条件时，该任务将N个节点移到N个截断的八面体质心。

如图4所示，为任务分配的二分图模型。其中，d i，j为二分图边缘的权重，其距离矩阵如式(6)所示:

图4 任务分配问题的二分图模型

问题的目标函数如式(7)所示:

式中:f1和f2是考虑了总移动距离和分移动距离的均匀性适应度函数；w1和w2分别是适应度函数f1和f2的权重。其中，f1和f2的数学表达如式(8)所示:

其约束条件定义如式(9)所示:

2 基于蝙蝠优化器的节能覆盖算法

2.1 蝙蝠优化器

自然界中，蝙蝠会根据自身的口味、饥饿程度、猎物的血量以及狩猎的风险分析目标。然后，根据兴趣程度选择目标猎物并参加捕食竞争，这种现象被称为蝙蝠的利己行为。

受蝙蝠利己行为和利他行为的启发，本文提出了一种蝙蝠优化器(VBO)，以最大化所有蝙蝠的收益。最终，将VBO用于优化重新部署期间节点的能耗。其中，VBO的构建步骤如下:

步骤1:找到每个蝙蝠的最佳猎物

首先，初始化各蝙蝠对猎物的兴趣值、风险值和蝙蝠的基因值。将第i个蝙蝠和第j个猎物视为b i和p j，并将b i在p j中的兴趣值、b i的基因值以及在第t次迭代中的狩猎风险值视为

计算每个蝙蝠捕获每个猎物的收益，b i在第t次迭代中捕获p j时的收益计算如式(10)所示:

将第t次迭代中b i的最佳猎物定义如式(11)所示:

步骤2:捕食比赛

在所有蝙蝠都拥有不再冲突的最佳猎物前，掠夺性竞争不会消失，所有蝙蝠的利益也无法最大化。在发生捕食冲突的情况下，在第t次迭代中被多个蝙蝠抢劫的猎物表示为中抢劫猎物所涉及的蝙蝠表示为集合然后遍历中的所有猎物和相应的蝙蝠，更新兴趣矩阵并返回步骤1。

步骤3:回送

至此，整个蝙蝠种群的利益已实现最大化，蝙蝠开始吸收血液。定义每个蝙蝠吸收的血液量如式(13)所示:

式中:τ1和τ2分别是衡量饥饿差异和b i与b j间遗传相似程度的阈值。若多个蝙蝠满足回送条件，那么b j的适应性值最大，则可以将b j定义为b i的最佳输血目标，其适合度值如式(14)所示:

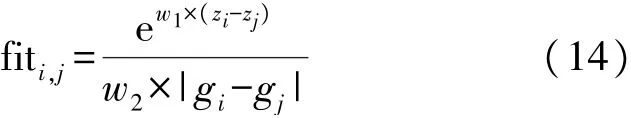
式中:w1和w2分别是饥饿差异的权重以及b i和b j之间的遗传相似程度。一旦没有蝙蝠需要输血，回送过程立即结束，此时各蝙蝠抽取的血量可得到有效平衡。

2.2 使用VBO优化节点的能耗

本文将节点移动到截角八面体质心的任务分配问题视为蝙蝠的狩猎问题，并用VBO解决多目标优化，该问题可最大程度地减少总能耗，并平衡节点的剩余能量，其过程如下:

步骤1:找到每个传感器节点的最佳目标

鉴于VBO步骤2用于最大化整个蝙蝠种群的利益与重新部署过程中传感器总能耗的最小化相反。因此，从传感器节点到截角八面体的相对距离被认为是蝙蝠捕猎时的最优距离。为确定传感器节点的最佳移动目标，可以通过式(15)确定第t次迭代中S i的最佳移动目标。

移动任务矩阵的数学表达如式(11)所示:

步骤2:竞争

当节点选择最佳移动目标时，等效于蝙蝠狩猎的相互冲突，节点目标的竞争过程与VBO的步骤2相似。在发生冲突的情况下，将冲突的目标视为感兴趣目标，将冲突的传感器视为活动的传感器，表示为集合然后遍历所有感兴趣的目标和相应的传感器，以更新利益矩阵并返回步骤1。

步骤3:交换移动任务

假设所有传感器节点都按照步骤2之后的移动任务立即移动，则每个传感器节点的移动距离将存在显著差异，等效于掠夺性竞争结束后每个蝙蝠吸收的血液量不同，将导致某些传感器节点的移动难以实现。

竞争后，所有传感器节点开始寻找其他节点交换任务，并根据任务交换定理交换节点S i和S m的移动任务。

任务交换条件:对于节点S i及其移动目标G i，以及节点S m及其移动目标G n，任务交换条件如式(18)所示:

等效于判断蝙蝠间的遗传相似度和饥饿度的差异是否满足式(13)中所述的回送条件。

任务交换定理:如果节点S i和S m满足任务交换条件，则可通过任务交换平衡它们的移动距离，其数学表达如式(19)所示:

任务交换定理:根据任务交换定理，如果有K个满足任务交换条件的节点，即可得到K个方案。如果S m的适应性值最大，则将S m定义为S i的最佳可交换节点，并通过式(19)交换S i和S m的任务。节点S m的适应度值如式(20)所示:

式中:μ1和μ2分别是交换移动任务后S i和S m移动距离之和和移动距离之差的权重。当没有传感器节点满足任务交换定理时，即认为交换任务过程结束。

3 实验结果与分析

3.1 参数设置

为了验证本文算法的性能，在相同实验条件下将本文算法与三维虚拟力算法(3DVFA)、虚拟力导向粒子群优化算法(VFPSO)、匈牙利算法(HA)进行对比试验。其中，VBO的主要参数如表1所示。

表1 VBO的仿真参数

3.2 仿真比较

如图5所示为VBO设置的传感器节点的初始位置。如图6所示为四种算法的传感器节点的最终位置和最终覆盖效果对比图。由图6可知，VBO和HA在最终覆盖效果和传感器节点的移动距离方面优于3DVFA和VFPSO算法。

图5 四种算法节点的初始位置

图6 比较四种算法的移动和最终覆盖效果

图7 所示为四种算法的运动轨迹，由图7可知，VBO和HA的移动轨迹比3DVFA和VFPSO短，且HA算法中移动距离较长的节点移动任务已在VBO中进行了优化。

图7 比较四种算法的运动轨迹的三视图

如图8所示，为四种算法的覆盖率比较结果。由图8(a)可知，HA和VBO的最终覆盖率均达到100%，而VFPSO和3DVFA仅达到96.42%和98.07%。假设四种算法的最终覆盖范围不同，因此图8(b)中比较了四种算法都达到95%覆盖率时的总能耗。由图可知，3DVFA和VFPSO的总能耗分别为9.1123×104J和5.5642×104J，比VBO算法少253.86%和116.08%。但是当达到完全覆盖范围时，VBO消耗了4.1231×104J的能量，比HA低6.76%，牺牲了将总能耗降至最低的性能。由此可知，在剩余能量的均匀性和最大能耗节点能耗方面，VBO的表现明显优于其他算法。

图8 四种算法的覆盖率比较

如图9所示，为四种算法每个节点的能耗。由图可知，在同时考虑总能耗和节点能耗均匀性的情况下VBO表现性能最佳，3DFVA表现最差，VFPSO略优于3DVFA，HA明显优于3DVFA和VFPSO。与HA相比，VBO最大能耗节点的能耗和均匀性都得到了有效降低，这是由于在步骤3中交换了长短移动距离节点任务，而3DVFA和VFPSO仅将最终覆盖范围作为优化的目标，忽略了能耗的优化，从而导致了性能差异。

图9 四种算法每个节点的能耗比较

如图10所示，为四种最大能量消耗节点的能量消耗和剩余能量的均匀性比较结果。图10(a)为四种算法的最大能耗节点的能耗比较结果，由图可知，四种算法的最大能耗节点在运动20、24、32和51轮后达到最佳位置，其能耗分别为340.67 J，405.59 J，545.40 J，以及891.84 J，表明在该性能指标上，VBO的效果均优于其他三种算法，分别为61.80%、37.54%和16.01%。如图10(b)所示，3DVFA，HA，VFPSO和VBO运动后的剩余能量均匀度为173.28 J，107.99 J，81.42 J和69.43 J，表明3DVFA，HA和VFPSO的性能表现分别比VBO低59.93%、35.71%和14.72%。

图10 最大能量消耗节点的能量消耗和剩余能量均匀性比较结果

为评估VBO的性能，在传感器节点的不同初始位置使用2.5 GHz频率和8 GB内存的计算机进行多次独立仿真，以提高相同条件下实验结果的可靠性。如图11所示为3DVFA、VFPSO、HA和VBO在200个独立实验中最终覆盖范围的性能比较结果。由图可知，3DVFA的性能最差，其上下浮动约为95%，VFPSO的最终覆盖率平均值约为97.5%，略高于3DVFA。而HA和VBO的性能相同，且每个实验的最终覆盖率均可达到100%。

图11 200个独立实验下四种算法的最终覆盖率

如图12所示，为通过200个独立实验比较下的四种算法的能耗对比结果。其中，图12(a)为通过200个实验完成四种算法移动任务后的总能量消耗对比。由图可知，其中3DVFA和VFPSO算法分别在9.5×104J和8.5×104J附近波动，而VBO的平均值接近6.8×104J，比HA略低，但明显优于3DVFA和VFPSO算法结果。图12(b)和图12(c)分别为通过200个独立实验显示的四种算法的最大能耗节点能耗和剩余能量均匀性性能比较结果，由图可知VBO的性能明显优于其他三种算法。

图12 200个独立实验比较四种算法的能耗

将200次实验下四种算法的性能差异平均化，得到表2与图13中所示结果。由表2和图13可知，与其他算法相比，VBO策略可将节点的剩余能量的平衡效果分别提高32.03%、43.44%和30.53%，最大能耗节点能耗降低了16.06%、39.78%和29.55%。同时，与3DVFA和VFPSO相比，VBO算法可将节点的总能耗降低30.04%和22.79%。此外，在最终覆盖率和时间消耗方面，所提VBO算法也具有良好表现。由此，经上述对比分析论证可知，所提VBO算法具有良好的可靠性与准确性。

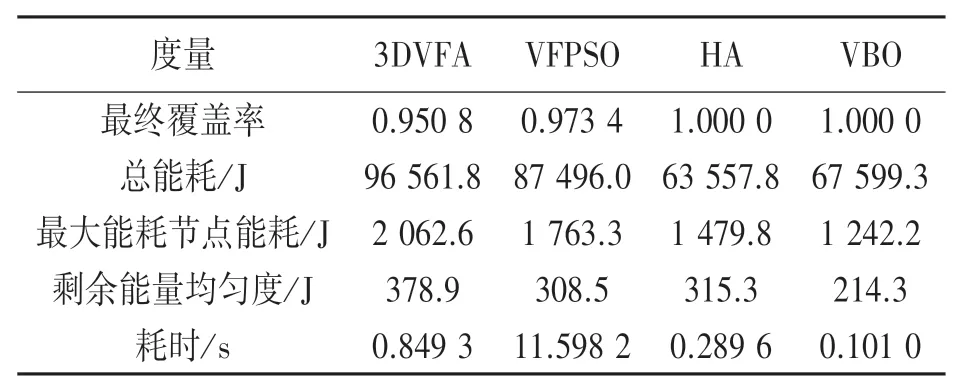
表2 200次实验下平均结果的性能比较

图13 200次实验的平均结果的性能比较

4 结论

针对复杂和恶劣环境下，三维无线传感器网络传感器节点电池充电和恢复受阻的问题，提出了一种基于蝙蝠优化器的三维无线传感器网络节能覆盖增强策略，并通过仿真对比实验得出以下结论:①提出了一种基于蝙蝠优化器的能量优化算法，将网络节点覆盖增强和能量优化的问题转化为将节点移动到截角八面体形心的任务分配问题，简化了计算方式，提高了计算精度。②与传统的3DVFA、VFPSO、HA策略相比，所提基于VBO的策略能使节点剩余能量的均匀性分别提高30.53%、43.44%和32.03%，且在总能量消耗、最终覆盖率和时间消耗等方面均优于对比策略，表现出优良的可靠性与准确性。③本文研究尚缺乏对传感器节点相同感知半径约束的考虑，因此在后续研究中，将针对传感器节点相同感知半径约束开展进一步研究。