热式气体质量流量计动态响应的优化*

刘家旭，徐 英，张 涛*，王念榕

(1.天津大学电气自动化与信息工程学院，天津300072；2.天津市过程检测与控制重点实验室，天津300072；

(3.中国石油规划总院，北京100083)

热式气体质量流量计在测量过程中，其动态响应时间过长的现象一直存在，并且在实际生产中也存在。热式流量计响应时间过长本质是流量传感器的热电阻响应时间过长导致的[1－4]。很多的工业场合需要对流量进行实时连续测量，但被测流量值可能不断发生变化，此时，准确实时的测量其流量需要缩短热式响应时间，方可实现快速测量。

1 热式气体质量流量计的基本原理

热式流量测量技术最早起源于20世纪60年代热线式传感器的应用，其作为流量测量技术的一个重要分支，是一种基于热传递原理的直接式质量流量测量方法[5－6]，利用流动中的气体与热源之间的热量交换关系直接测量气体的质量流量。热线式传感器电阻直径通常只有几十微米，其热响应速度较快，不存在响应速度慢的问题，但为了在工业应用有更好的可靠性，使传感器不易损坏，目前工业常用的热式流量计中传感器电阻直径为2 mm~3 mm，与热线式传感器相比，会出现响应时间长的问题。热式气体质量流量传感器的原理如图1所示。

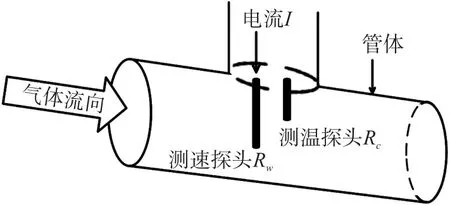
图1 热式气体质量流量传感器的原理图

热式气体质量流量传感器由两个探头组成[7－8]，分别称为速度探头R w和温度探头R c。速度探头通以电流，被加热到高于被测气体的温度；温度探头测量气体的温度。当气体流过两个探头，并且达到稳定状态后，探头与周围介质会达到一个动态平衡传热过程。根据牛顿冷却公式[9]，可以认为测速探头的加热电功率等于其表面对流换热的耗散热量，如式(1)所示，左侧是测速探头加热的电功率，右侧是对流换热量:

I为测速探头的供电电流，R w为速度探头的电阻值，h为测速探头对流表面换热系数，A为测速探头的外表面积，T w为测速探头的温度，T c为测温探头测量的流体温度。

式(1)中的传热系数h与很多因素相关[10]，通常由努塞尔数Nu与其构建相关的联系，Nu定义式为:

式中:λ为气体的导热系数，d是特征尺寸(本研究中d取测速探头直径)。

可以将对流换热过程视为气体横掠单管的换热过程，换热壁面上的流动边界层与热边界层都无法充分发展，所以目前大多数研究从实验角度分析气体横掠单管的对流换热规律。在众多的经验公式中[11－12]，Hilpert提出的气体横掠单管的经验公式应用比较广泛[13]，如式(3)所示，

式中:C与n在本次研究中的取值由具体实验数据拟合得出，参数m根据文献[4]的经验值取1/3。Re称为雷诺数，是表征气体流动情况的无量纲准则数，其定义为:

式中:ρ为气体的密度，v为气体的流速，μ为气体的动力粘度。

式(3)中的Pr称为普朗特数，是反映气体物性参数变化的无量纲准则数，其定义为:

式中:C p为气体的定压比热容。

联立式(1)至式(5)可得到测速探头所测的质量流量G:

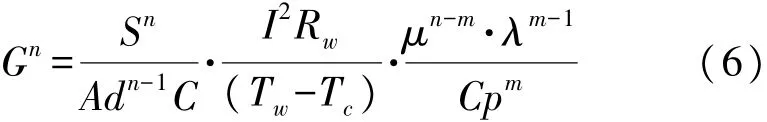
式中:等式左边为气体的质量流量，定义为:

式中:S为测量管道的横截面积。等式右边分为三个部分，

常值系数:

功率温差比:

物性参数:

2 响应时间数学模型

在工业现场的热式测量过程中发现，流量发生变化的过程中，热式测量信号会出现滞后现象，如图2所示。

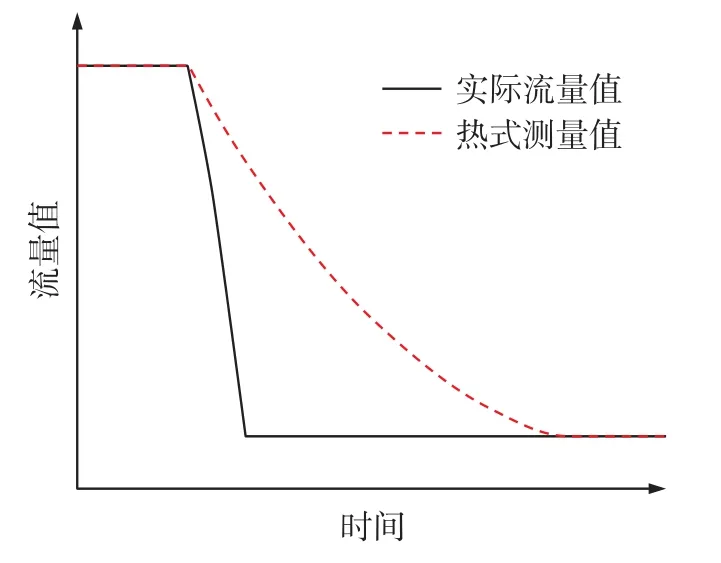
图2 热式测量信号滞后被测流量值

为了深入研究热式测量过程中响应时间的原因与影响因素，从传热学机理出发，构建了热式响应时间的数学模型。

根据传热学原理，温度变化的过程需要一定时间，称为响应时间，响应时间产生的主要原因为被测流量的变化会导致探头的对流换热量发生变化，根据热传导原理，测速探头测量的温度会产生滞后。

测速探头温度滞后的时间是探头内部热传导的时间，根据传热学中热传导原理如式(11)所示[10]。

式中:ρ′、c分别为测速探头的密度与比热容，T w表示温度，t代表时间，Φv表示广义的热源，代表单位体积单位时间内产生的热量。

探头的广义的热源存在两个，一个热源为供电电流加热，这里称为内热源，可以表示为:

式中:Φv1为内热源，代表其单位体积单位时间内产生的热量，V表示探头发热部分的体积。

另一个热源为流体流过探头时对流换热量，称为外热源，可以表示为:

式中:Φv2为外热源，代表其单位体积单位时间内产生的热量。由于外热源对探头实际作用是冷却的，因此外热源Φv2是负热源。

所以广义的热源Φv可以视为外热源与内热源的叠加，如式(14)所示。

在稳定测量过程中，探头周围的温度达到热平衡，无温度的阶跃变化，可以认为Φv1＋Φv2＝0，结合式(12)与式(13)可以得到热式原理中的牛顿冷却公式，如式(1)所示。

但是，在流速变化的过程中，测速探头对流换热的热平衡因为流量变化而被破坏，并且还未达到新的热平衡，热式流量测量的响应产生滞后的时间就是之前的热平衡被破坏到新的热平衡形成的过程。

这个过程中，Φv1内热源不变，Φv2发生变化，所以式(11)的等式不成立，且如果该过程是流速增大的过程，则外热源Φv2数值增大，由于Φv1不变，Φv1<Φv2，如果该过程是流速减小的过程，外热源Φv2数值减小，由于Φv1不变，Φv1>Φv2，所以从流速改变，到热平衡达到稳定之前，探头的导热过程由式(11)表示，联立式(11)与式(12)、式(13)、式(14)可得，

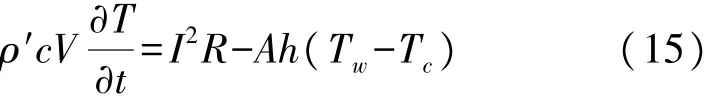
引入初始条件t＝0，也就是流量开始变化的时刻，此时刻的测速探头温度为T0，对式(15)的微分方程求解为:

从式(16)中，可以得出热平衡形成过程中，测速探头的温度T w与T0、T c、供电电流I、换热系数h等多个因素有关，而热平衡的响应时间的影响因素为测速探头的物理参数，如测速探头的密度ρ′、测速探头的比热容c、测速探头发热部分的体积V，除探头自身的参数外，换热系数h也是影响响应时间的重要因素。

记测速探头的温度最终稳定为T1，通过式(16)将时间t取正无穷即可，可得到，

在式(16)中，可以看出温度随时间的滞后为指数形式，当指数部分为－1的t值，记为时间常数τ:

将式(18)的时间常数τ代入式(16)，可得在τ时刻的测速探头的温度Tτ:

可以得到e－1≈0.368，所以时间常数τ可以理解为，温度T0过渡到T1的过程中，已经过渡了T1＋0.368*(T0－T1)的过程需要的时间，也就是从温度T0过渡到温度[T0－0.632*(T0－T1)]所需要的时间，如图3所示。

图3 时间常数τ的意义

结合热式原理计算中的式(2)~式(5)，可推导出换热系数h的关系式，换热系数h可表示为:

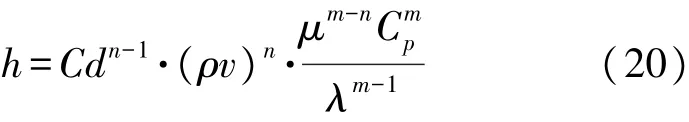
由式(20)可以看出，换热系数h与三个因素有关系，分别为常值Cd n－1、质量流速相关量(ρv)n、物性相关的参数

将式(20)代入到τ的表达式(18)中，可以得到:

时间常数τ与三部分因素有关，分别为探头的材料与体积相关的参数、质量流速的倒数物性相关的参数

如图2所示，在热式流量计响应过程中，流量计外部的流速已经为最终流量计稳定后的流速，即为式(21)中的流速v，因此热式时间常数τ大小仅与最终的流速有关，与流速变化以前的流速无关，且流速v越大，时间常数τ越小；流速v越小，时间常数τ越大。从这也可看出中低流速的响应时间较长，在中低流速范围减小响应时间更有意义。

3 利用时间常数τ提前预测质量流量

由式(22)可知，对于同一流体，时间常数τ与质量流速倒数的n次幂成正比，此质量流速为待预测的质量流速，所以也与质量流量成正比，这里用G1表示待预测的质量流量，由式(22)可求出G1的具体表达式，如式(22)所示。

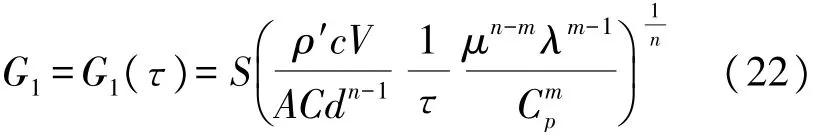
因此只需求出时间常数τ即可通过式(24)预测出质量流量G1。由于被预测的质量流量G1是确定值，时间常数τ是唯一确定的，式(23)有唯一解。

由图3可知，时间常数τ是在过渡的过程，探头温度由T0过渡到[T0－0.632(T0－T1)]的时间。探头温度与探头所测量的质量流量一一对应，所以时间常数τ为G0过渡到G0－0.632(G0－G1)的时间，将τ时刻的质量流量计算值记为f(τ)，所以可得:

联立式(23)、式(24)可得:

式(25)等号右边C m与n为与过度过程无关的参数，且这些参数可以在求G1的时候拟合确定。

在工业现场热式流量计应用中，待测流量发生变化后，变化过程的流量可由热式流量计测量，即通过式(6)计算得出质量流量G。

因此，可以通过迭代的方式求解式(25)中的τ。首先通过热式测量可以知道流量变化前的流量G0，由于时间常数最小可能值是2 s，因此设定其初始值τ＝2 s，接着根据τ通过式(25)计算出f(τ)，同时通过热式测量得到该时刻的质量流量，记τ时刻测量得到的流量测量值为G(τ)，将f(τ)与G(τ)进行比较，如果二者一致，则说明此时的τ即为时间常数。如果不一致，将τ＝τ＋0.5 s，再进行计算比较，直至找到时间常数τ为止，详细的迭代过程中如图4所示。

图4 预测流量G1迭代求解流程图

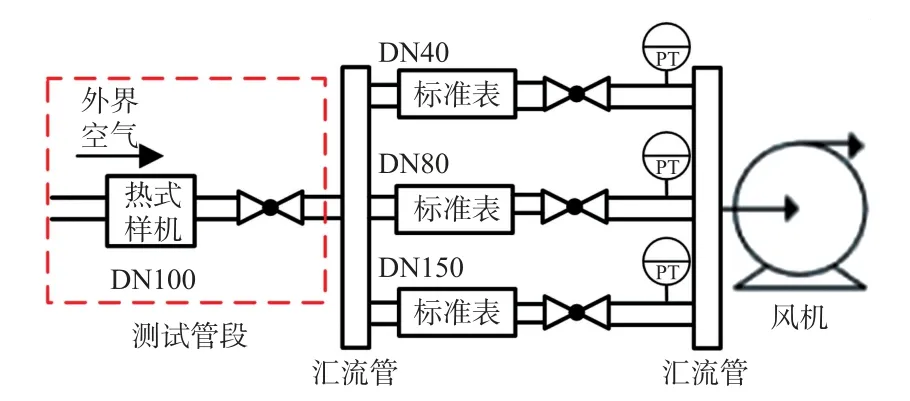
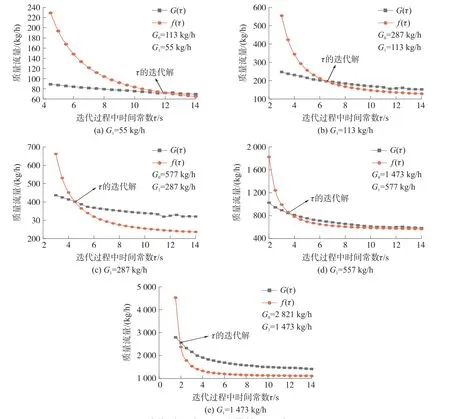
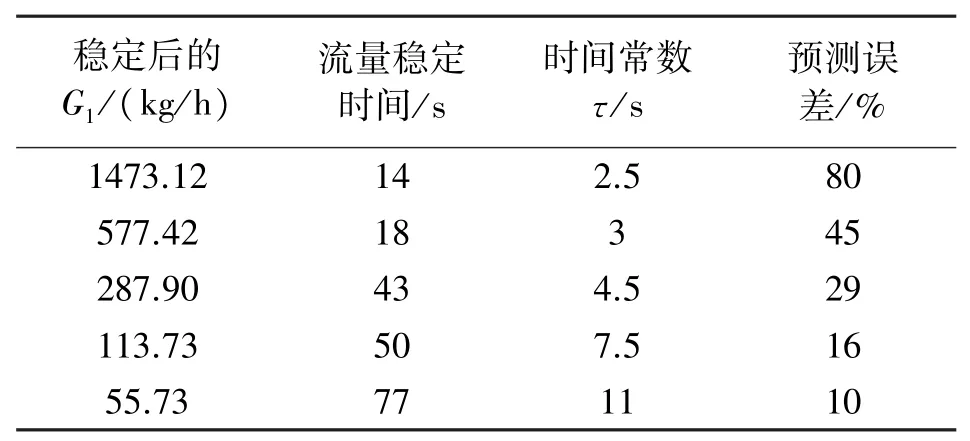
由于热式流量计硬件电路采样频率的限制，所以设定每次τ递增0.5 s，根据式(25)可知，时间常数τ越小，f(τ)越大，所以考虑到实际的流量情况，初始值τ＝2s较为合理，既不会错过τ而导致无解，也能提高计算效率，同时f(τ)由高到低递减，迭代一开始τ较小的时候，f(τ)>G(τ)，所以判定依据为f(τ)

通过迭代求解出时间常数τ的值，进而通过式(22)预测出待预测的质量流量G1，从而解决了热式气体质量流量计响应速度慢的难题，提高了响应速度。

4 实验验证分析

实验所用装置是在天津大学流量实验室的常压气体装置进行的。实验装置采用微负压法，通过调节风机的频率来调节气体流量。标准表由多路并联的涡轮流量计组成，精度为0.5%，口径分别为40 mm、80 mm、150 mm。实验测试管径为DN100，实验的工况条件选取常温常压，测量介质为空气。实验装置原理如图5所示。

图5 实验装置原理图

实验的流量点如表1中所示。通过对实验数据的分析来进一步验证上一节中的提前预测稳定后的流量来减少响应时间的方法。按照上一节的方法，首先分析实验数据，以图6为例，从图中可提取到流量稳定的时间，进而根据式(24)，结合图中起始流量G0＝110 kg/h与稳定后流量G1＝55 kg/h，在图中提取出时间常数τ。提取后的稳定时间与时间常数τ如表1所示。

图6 G1＝55 kg/h时的动态响应过程

表1 不同流量点的稳定时间与时间常数τ

在时间常数τ时刻即可预测出流量稳定时的质量流量G1，相比于流量稳定时间较为提前，尤其在中低流速响应时间减少更明显，如在G1＝55 kg/h的流量下，从原本稳定时间77 s减少到11 s，提升了测量效率。

通过式(22)可知，在物性参数不变的情况下，时间常数τ与质量流速的n次方的倒数成正比，如图6所示。可以得出实验中的时间常数τ与待预测质量流量G1确实存在式(21)的关系，进一步验证了上一节中提出的数学模型。

通过图7分析，可以得出时间常数τ与质量流速v的关系，如式(26)所示:

图7 时间常数τ与1/(ρv)n的关系

按照流程图4，进行时间常数τ的迭代，通过(26)即可得出f(τ)的表达式，通过热式流量计的测量可得到G(τ)，也就是如图6的数据。然后计算P＝f(τ)/G(τ)，不同流量点下的f(τ)与G(τ)如图8所示。

图8 迭代过程中不同流量的f(τ)与G(τ)

从图8中可看出，不同流量点对应的时间常数τ，即f(τ)与G(τ)曲线相交处对应的时间为该流量处的时间常数τ。

求出时间常数τ之后，根据式(26)即可求出预测的质量流量。通过实验数据的分析，验证了上一小节预测流量G1方法的可行性，同时减小了响应时间，使得热式气体质量流量计的响应速度得到了提升，如图9所示，阴影部分为加入预测后比未加入预测提高的效果。

图9 加入预测方法的示意图

通过提前预测稳定后质量流量G1的方法来减小热式流量计的响应时间，一定程度上提高了热式流量计的响应速度，但是，流量变化的前几秒流量变化十分迅速且由于实验过程中的数据采集每0.5 s采集一个数据，所以最终以此方法得到的时间常数τ的误差为±0.5 s。

根据表2分析，当时间常数τ的误差0.5 s时，预测流量值G1的预测误差随着G1的流量的增大而增大，而且气体的流速越大，响应时间τ越小；气体的流速越小，响应时间τ越大。

表2 不同流量下预测的误差

热式测量的流量较大时，热式气体质量流量计的响应速度较快，尤其质量流量大于580 kg/h时，达到稳定的时间在20 s以内，但是预测的误差却高达45%以上，如果采用此方法进行预测，由于流量变化急剧，这种情况下响应时间τ为0.5 s对预测结果误差较大，但由于该流量下本身响应速度较快，所以利用该方法预测流量的意义不大；热式测量的流量较小时，尤其质量流量小于300 kg/h时流量时，响应速度慢，达到稳定的时间需要40 s以上，预测的误差在30%一下，尤其在100 kg/h一下的流量预测，预测误差在16%以内。

因此综合考虑，在中低流速的测量中，利用此方法对其流量进行预测，能够大大减少响应时间，能够将响应时间缩短80%~90%，虽然会因此增大10%~30%的误差，但是大大缩短了响应时间，提前预测到流量值还是很有意义的。

5 总结

本文研究了热式气体质量流量计在测量过程中，实际的流量发生变化且还未达到稳定过程中的热式传感器探头附近的传热机理，构建了相应的数学模型，通过模型中相关物理量可知导致热式气体质量流量计测量过程中动态响应时间过长的因素，并通过实验得出了响应时间τ与稳定后质量流量G1的规律。提出了将传热理论及时间常数τ定义推导的f(τ)与由热式传感器实时测量的G(τ)进行迭代的方法，在时间常数τ时刻提前预测出稳态时的质量流量G1，缩短了响应时间。运用该方法将预测流量G1和实测流量G的切换，在流量发生变化时采用预测流量G1，在流量稳定时采用实测流量G，很好的解决了热式动态响应测量的滞后问题。

但是该方法缩短响应时间的同时，预测的稳态时的质量流量与实际的流量存在一定的偏差，并且实验数据表明稳态时的质量流量越大，偏差就越大，所以此方法适用于响应时间较长的中低流速，效果尤为明显，能够将响应时间缩短了80%~90%。由于高流速本身的响应时间较短，如果仍采用此方法针对高流速减小响应时间，缩短的时间有限，实际意义不大，且与中低流速相比较，预测的误差较大。