基于Dijkstra 算法的输电线路人工巡检优化方法
2021-07-16姚红芳马蔡国张俊婷许金彤
秦 奋,姚红芳,马蔡国,张俊婷,倪 涛,许金彤
(国网浙江省电力有限公司杭州供电公司,杭州 310009)
0 引言
输电线路是电力系统的重要组成部分,其安全运行是系统整体稳定的重要保障。输电线路及其附属设备暴露在野外,其运行方式必定会受到环境因素、人为因素和设备自身因素等的影响,线路巡检已经成为必不可少的运维任务。随着经济建设对电力需求的日益增长,线路巡检成本越来越高。
目前,国内输电线路巡检方式主要有人工巡检、无人机巡检和车辆巡检等[1-3]。在车辆巡检和无人机巡检应用中存在很多人工智能算法优化巡检路径[4-5],其中包括粒子群算法、遗传算法和蚁群算法等智能算法,利用智能算法在无人机和车辆巡检中可以科学合理地对巡检路径进行规划,提高巡检效率。但由于输电线路环境的复杂性,很多情况无法采用汽车巡检和无人机巡检,必须依靠人工。传统人工输电线巡检路径规划大多由有经验的巡检员制定巡检路径,这种依靠经验的方式存在很强的主观性,缺乏科学性和客观评价体系,因此存在着人力的浪费和塔杆、线缆井等设备巡检不到位的情况[6-8]。对输电线路人工巡检路径进行优化,可以有效提升巡检效率,并能输出有效数据以建立客观评价体系,避免设备巡检不到位或被多次巡检,以节省人力资源和费用,因此具有重要意义[9-10]。
Dijkstra(狄克斯特拉)算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,它是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题[11-13]。Dijkstra 算法的主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止[14-15]。目前,该算法在农业、化工和网络等领域得到了广泛的研究和应用。但在输电线路巡检领域,基于Dijkstra 算法的路径规划方法的研究还很少。与遗传算法等智能算法相比,Dijkstra 算法计算简单、运行时间短,在全局信息已知、静态规划中,采用Dijkstra算法更加方便快捷。
因此,本文采用Dijkstra 算法研究输电线路人工巡检路径的优化方法,通过规划最短巡检路径,从而提高巡检效率。
1 基于Dijkstra 算法的路径规划方法
1.1 Dijkstra 算法基本原理
Dijkstra 算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
假设V 是所有路径中包含顶点的集合。将V分成2 组,第一组为已求出最短路径的顶点集合,记为S;第二组为其余未确定最短路径的顶点集合,记为U。初始状态时,S 中只有一个源点,以后每求得一条最短路径,就将其加入到集合S 中,直到全部顶点都加入到S 中为止。在加入的过程中,总保持从源点v 到S 中各顶点的最短路径不大于从源点v 到U 中任何顶点的最短路径。Dijkstra 算法的一般步骤如下:
(1)初始时,S 只包含起点s;U 包含除s 外的其他顶点,且U 中顶点的距离为起点s 到该顶点的距离。U 中顶点v 的距离为(s,v)的长度,若s和v 不相邻,则v 的距离为∞。
(2)从U 中选出距离最短的顶点k,并将顶点k 加入到S 中;同时,从U 中移除顶点k。
(3)更新U 中各个顶点到起点s 的距离。
(4)重复(2)和(3),直到遍历所有顶点。
1.2 基于Dijkstra 算法的路径规划
根据Dijkstra 算法的基本策略,人工巡检路径规划的方法流程如图1 所示。

图1 基于Dijkstra 算法的人工巡检流程
首先,提取线路上设备的唯一名称和GIS(地理信息系统)坐标信息。由于线路上设备的命名规则按照国家电网统一规则(线路名称+设备编号),因此每个设备的名称是唯一的,并将这些信息作为该节点信息保存。按照预先设定好的GIS 信息精度要求,对系统中的所有节点GIS 信息的经度和纬度数据进行比较。将符合精度要求的、经度和纬度数据认为是一致的GIS 信息进行合并,只保留GIS 信息一致的节点编号较小的节点信息,并将一个或多个GIS 信息一致、节点编号较大的节点信息从系统列表中删除。
其次,根据各个节点之间的GIS 坐标信息或已知路径来计算各节点之间的路径长度,并保存在路径向量列表中。路径向量列表包含以下数据:起始节点编号,终点节点编号,路径长度(向量),路径属性。由于线路巡检包含地上(塔杆)和地下(线缆井),在计算路径规划之前将地上(塔杆)和地下(线缆井)做为限制条件对线路属性进行分类拆分。则一条完整的线路中,可以有3 种情况:只由地上(塔杆)的路径属性组成一条完整的线路;只由地下(线缆井)的路径属性组成一条完整的线路;由1 段或多段地上(塔杆)的路径属性和1 段或多段地下(线缆井)的路径属性共同组成一条完整的线路。
最后,采用Dijkstra 最短路径算法来对输电线路中的所有路径向量列表进行巡检路径规划。对于以节点表示的线路列表中的每一个节点进行检测,按照节点编号从小到大的顺序进行排列的每个节点都通过其2 个节点之间的路径向量进行连接。如果该线路上的所有节点都被检测到了,说明该条线路已完成巡检,则此时的路径即为最优路径。
2 输电线路人工巡检路径优化
2.1 Dijkstra 路径规划仿真
本文将Dijkstra 算法在仿真巡检节点上进行了验证,仿真的巡检路线节点包含A,B,C,D,E,F 共6 个节点,各节点之间的距离如图2 所示。
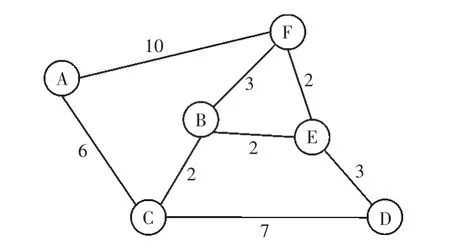
图2 路线节点示意
根据第1 节的Dijkstra 路径规划方法,规划的最短路径如图3 所示,路径距离总和为16 km。相比于其他路径,例如D-E-B-C-A-F 的总路径距离为23 km 或D-C-A-F-B-E 的总路径距离为28 km 等,基于Dijkstra 算法规划的路径距离得到了大幅缩减。

图3 规划的最短路径
2.2 输电线路巡检路径优化
为验证基于Dijkstra 算法的路径规划方法的有效性,对4 条输电线路进行了巡检路径优化。表1 列出了以4 条线路为例,按照国家电网统一规则命名的设备表格。

表1 设备名称
提取该设备的线路名称及该设备在该线路内的设备编号、GIS 坐标信息,将这些信息作为该节点信息进行保存。还是以表1 中4 条线路的设备信息为例,节点信息表格记录如表2 所示。

表2 节点信息表格记录
对符合精度要求、经度和纬度数据认为是一致的GIS 信息进行合并。合并后的信息如表3 所示。显然,在实际生成的优化巡检路径中,即使其设备在表1 中都属于同一条线路,地上(塔杆)/地下(线缆井)也是2 条毫不相关的路径。因此对表3 中只以地上(塔杆)的数据为例,建立地上(塔杆)路径向量列表,见表4。表4 中的数据为2 个节点之间巡检所需的时间。

表3 节点信息表格记录
为直观地表示,将表4 中的数据用图形化的方式进行表达,如图4 所示。
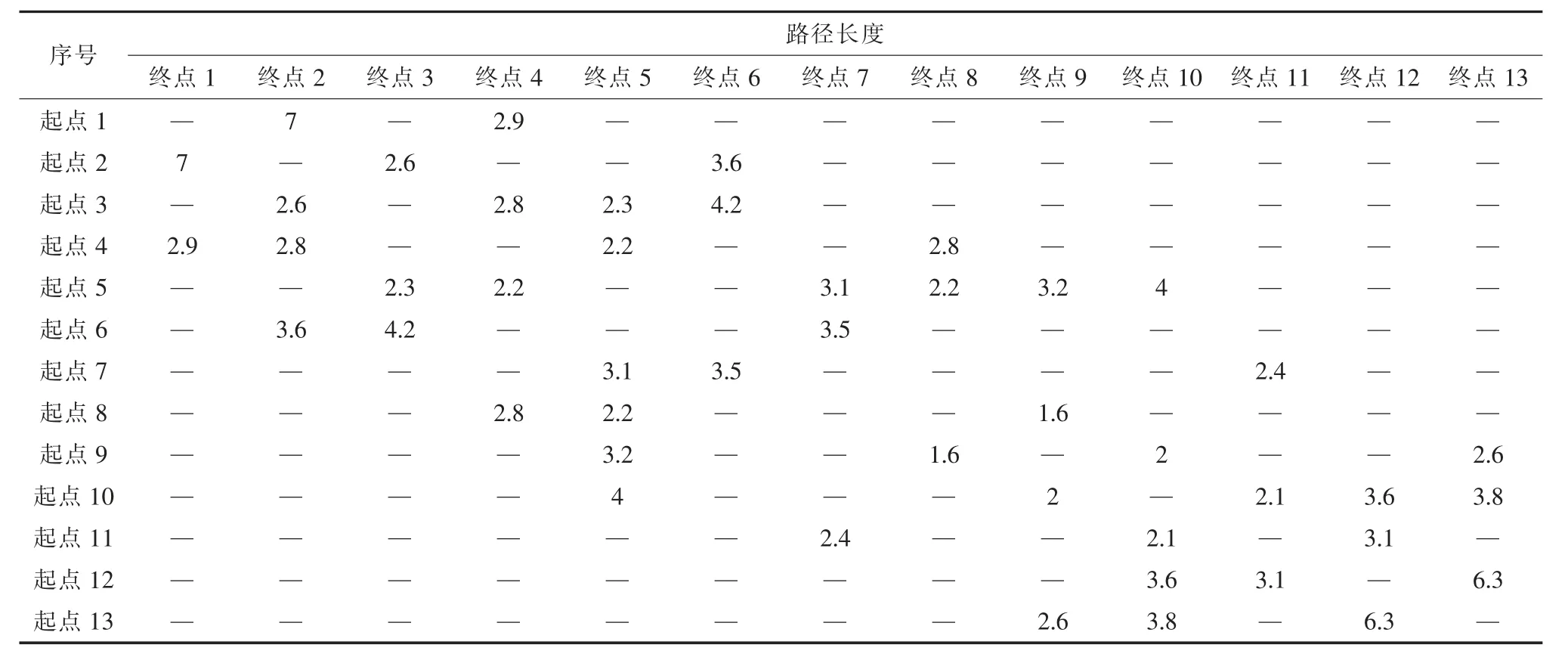
表4 地上路径向量列表 min

图4 地上初始巡检路径示意
根据Dijkstra 路径规划方法,将最优路径的结果用图形化的方式进行直观表达,如图5 所示。根据该规划路径,巡检完13 个塔杆所需的时间为33.6 min。而在常规巡检路线中,路线1-2-6-3-4-8-5-7-11-10-9-13-12 所需的巡检时间为41.1 min,路线1-4-8-9-13-10-5-3-2-6-7-11-12 所需的巡检时间为35.2 min。加上巡检人员的返程路径,Dijkstra 路径规划的总巡检时间为43.5 min,而常规路径的总巡检时间分别为53.8 min 和47.9 min。可见,Dijkstra 路径规划方法缩减了人工巡检时间,提高了巡检效率。
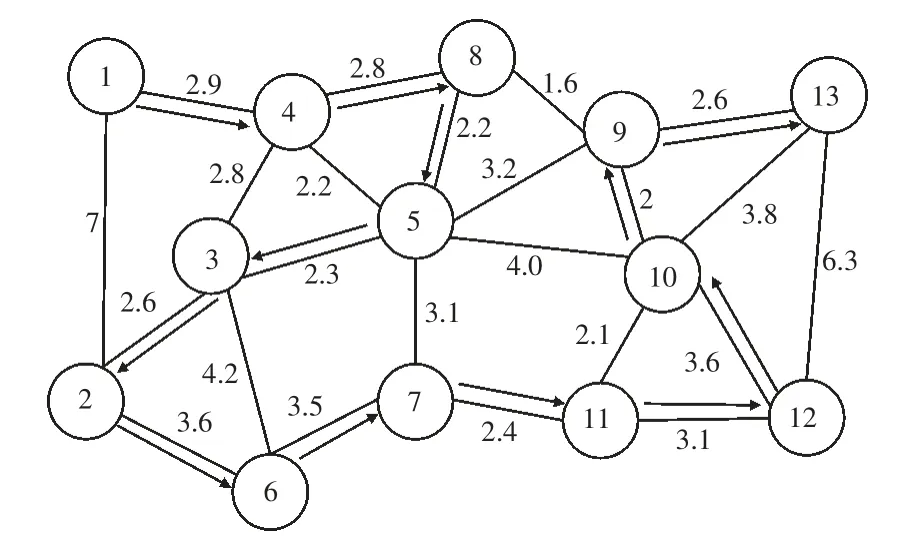
图5 地上最优巡检路径示意
此外,若设备信息或线路信息有变动,如增加、删除、修改GIS 信息和修改名称等,这些变动都会对节点信息或路径向量信息产生影响,因此需要重新计算。对此,可对巡检优化方法的系统设置定时计算周期,如果在设定的周期内发生上述信息的改变,则到了指定时间系统即开始重新计算优化路径;如果在设定的周期内未发生上述信息改变,则到了指定时间系统不做更新计算。
3 结语
本文采用Dijkstra 算法对4 条输电线路人工巡检路径进行了优化,算法考虑了巡检员巡检路径长度最小化和巡检线路属性的因素,科学制定巡检路径,巡检时间由常规的53.8 min 和47.9 min 缩短至43.5 min。该方法既适用于电力供电部门输电线路人工巡检的路径优化,也适用于配电线路人工巡检的路径优化。
