基于蒙特卡洛的配电网光伏消纳能力评估
2021-07-16张源渊贾俊青
郭 杉,张源渊,贾俊青,杨 洋
(1.内蒙古电力科学研究院,呼和浩特 010020;2.呼和浩特供电局,呼和浩特 010020)
0 引言
近年来,分布式光伏(以下简称“光伏”)因其环境友好、能够长期免维护运行的特性,成为中低压配电网中最常见的新能源发电形式。光伏并网,一定程度上可以缓解电网的供电压力,促进负荷的就地消纳,有效降低电压衰减及有功网损,但近年来,光伏并网呈现出单点容量逐渐增大、接入地区由城市电网转向农村电网的趋势,为配电网的安全稳定及经济运行带来了新的挑战。一旦接入位置及容量配置不合理,当系统轻载时,原有潮流流向改变,可引发并网局部过电压问题。故在光伏系统设计阶段,应评估配电系统消纳能力,进而确定光伏的最佳接入位置及容量[1-5]。另外还应充分发挥光伏自身的电压控制能力[6-11],在尽可能保障光伏的有功功率最大化的同时,将其对电网的影响降至最低。国内外关于光伏消纳及最优配置已展开了大量研究,根据原理差异可分为以下2 类[12-15]。
基于智能算法的方法。此类方法通常包含2个阶段。首先基于电压灵敏度、网损灵敏度等指标,确定光伏接入位置;随后以电压质量、有功网损为优化指标建立目标函数,通过遗传算法、粒子群优化等人工智能算法求解目标函数,确定接入容量。但此类方法通常只能得到局部最优解,而非全局最优[4]。另外,针对不同的场景,每次均需执行潮流计算,耗时较长。
基于随机场景的方法。该类方法通过改变负荷、光伏位置及容量创建大量随机场景[5],计算各场景的光伏消纳评价指标。文献[6]假设光伏出力及负荷状态独立,通过二者状态概率的卷积建立光伏发电-负荷混合概率模型,以节点电压、节点渗透率、支路传输电流、系统渗透率约束,实现光伏发电的选址和定容。当仿真场景足够多时,可全面掌握光伏消纳水平。此类方法面临的问题在于,随着配电系统规模扩大,需模拟的场景亦随之增多,将导致运算开销大幅提高,所以该类方法不适用于大规模配电系统。
本文首先分析光伏接入后对配电系统电压稳定性的影响,然后提出一种基于敏感度的电压估算方法,从而避免因场景改变而导致的大量潮流计算,利用蒙特卡洛模型确定配电系统的光伏消纳能力,考虑到运行条件的改变仍可能引起局部过电压,故提出一种有功-无功协同的并网点电压控制算法。最后通过Python 程序语言实现上述算法,并利用IEEE 33 模型对上述方法加以测试,试验结果验证了本文算法的有效性。
1 光伏接入对配电系统电压稳定性影响分析
基于二端配电模型,推导配电系统节点电压稳定判据,在此基础上分析光伏接入对电压稳定性的影响。
图1 中,节点i 为线路送端,节点j 为线路受端,节点i,j 的电压向量分别为Ui∠δi和Uj∠δj,节点j 功率为Pj+jQj,线路阻抗为Ri+jXi,可表示为:


图1 两节点配电系统
将式(3)带入式(1)有:

处理后有:

依据式(5)两边实部、虚部分别相等,将其处理为以受端节点电压幅值平方为变量的一元二次方程:

2 基于蒙特卡洛的光伏容量消纳方法
2.1 光伏消纳评价指标
本文以电压合格率、有功网损率(以下简称“网损率”)及容载比作为评估配电系统光伏消纳能力的指标。配电系统综合电压合格率是电压合格节点数与配电系统总节点数之比,该指标反映配电系统电压整体达标率。网损率为系统有功网损与系统总有功负荷之比。需要说明系统总有功为各节点有功负荷之和,不包含光伏的有功出力。容载比为配电系统负荷与系统极限容量之比。考虑到各条线路容载比不同,取全部线路中最大容载比作为系统容载比。
2.2 基于电压敏感度的节点电压估算方法
本节将给出一种基于电压敏感度的节点电压估算方法,通过该方法,可避免因多场景导致的大量潮流计算。首先推导电压敏感度计算公式,潮流平衡方程的极坐标形式为:

等式两边乘以雅可比的逆矩阵后有:

忽略光伏接入对相角的影响,只考虑电压幅值的改变,有:


根据公式可知,对于m 个节点(假设包含1个平衡节点,无PV 节点)的配电系统,首先执行牛顿-拉夫逊潮流算法,得到收敛后的平衡方程,即式(7),对其雅可比矩阵求逆。为2(m-1)阶方阵,从逆矩阵中提取子阵,得到各节点的电压敏感度,再利用式(10)即可估算各节点的电压增量。参考文献[11],可得到基于网损灵敏度的有功网损计算方法。
2.3 基于蒙特卡洛的光伏消纳方法评估
蒙特卡洛是一种概率统计方法,其思路为通过改变光伏接入位置及容量创建多个场景,计算各场景光伏消纳指标,按区间统计各类指标出现的频率,根据频率阈值确定安全接入容量。不参与调压的接入容量评估方法。
步骤1:输入线路基本参数、拓扑结构、负荷数据、单点光伏最大允许容量G,每个节点至少包含高峰、低谷及平均负荷数据。
步骤2:利用2.2 节方法计算节点电压及网损灵敏度因子。
步骤3:输入场景总数N,电压合格率、网损率及容载比限值及各指标允许越限频率阈值。
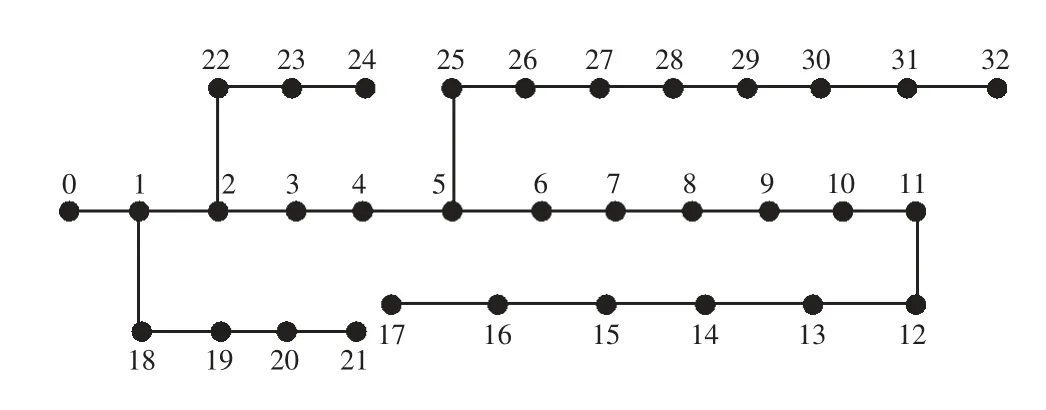
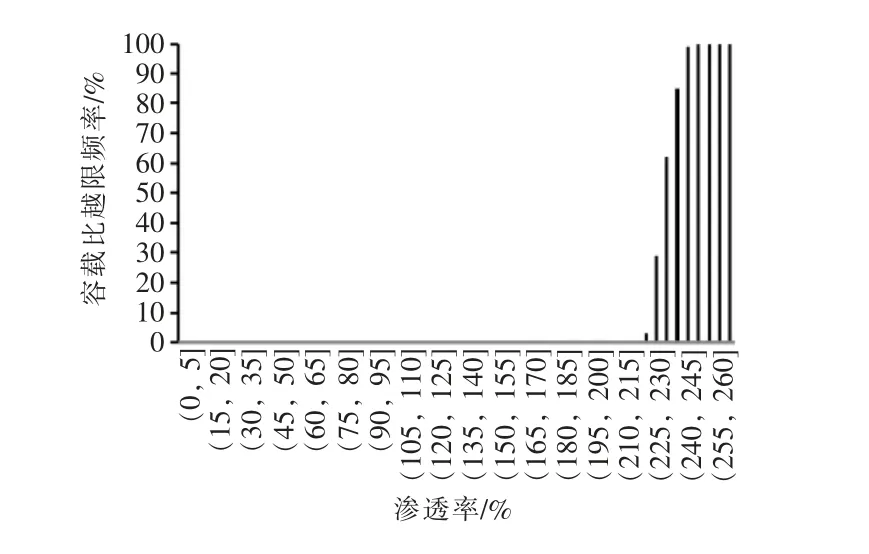
步骤4:利用步骤1 中参数,创建配电系统网架,从全部m 个节点中,随机选出k 个光伏接入结点,k 步骤5:若n 考虑到光伏参与调压后可提升系统消纳能力,故对上述方法加以改进,在步骤4 计算电压合格率后,若电压合格率越限,则光伏运行V-Q控制,由于无功功率的注入,原有电压估算方法不再适用,故执行潮流计算,重新计算评价指标。 本节从光伏控制模式入手,分析各模式的功率特性及模式间切换的触发条件,提出有功-无功协同电压控制方法。根据有功功率控制方法的差异,逆变器参与调压的控制方式可分为P-Q 解耦控制及P-Q 协同控制两类。解耦控制时有功及无功分别运行MPPT(最大功率点跟踪)及V-Q 模式。该模式下有功功率及无功功率控制解耦,逆变器根据直流侧I-V 特性曲线估算最大有功功率,并控制逆变器追踪该有功功率值。而无功功率执行V-Q 控制模式,控制曲线如图2 所示。 图2 中,横轴为并网点电压Upcc,纵轴为逆变器无功功率Qpv,[Vmin,Vmax]为节点电压正常运行区间,该区间运行时与外部无需进行无功交换,当Upcc低于节点电压允许下限Vmin时,控制逆变器发出无功功率,抬升Upcc,Qpv与Upcc呈线性关系,当无功功率达到极限容量Qmax后V-Q 模式失效,无法进一步调整Upcc;与之类似,当Upcc大于Vmax,控制逆变器吸收无功功率,当吸收无功功率达到极限值Qmax后,V-Q 模式失效。 图2 逆变器V-Q 模式控制曲线 逆变器功率特性曲线如图3 所示,由于逆变器具有双向无功调节能力,故主要工作于一、二象限。目前主流低压逆变器额定容量Smax满足Smax=1.1Pmax,功率因数最低可达0.9,从图3 中可以看出,当cosθ=0.9,S=Smax,此时逆变器具有最大无功调节能力,Qmax=0.44Smax。而当P=Pmax时,Q=0.42Smax。需要明确,尽管逆变器理论无功调节能力超过额定容量的40%,但运行中还受功率因数及容量制约,只在实际容量接近额定时,方能接近最大无功功率。此时,若Upcc仍越上限时将进入P-Q 协同控制模式,届时应通过削减有功功率,实现电压控制。 图3 逆变器功率特性曲线 尽管通过2.3 节的方法,可以确定配电系统的安全消纳容量,但配电系统运行是动态过程,一旦运行条件改变,仍可能出现局部过电压。分析P-Q 协同工作模式特性,该模式的控制目标为在保证电压合格的前提下,尽可能使有功功率最大,而无功功率最小,从而兼顾安全性及经济性。因而本文将P-Q 协同控制转化为2 目标多约束的优化问题,目标函数如下: 式中:第一项为t 时刻各光伏归一化的有功功率;第二项可视为t 时刻光伏总有功功率。约束条件包括等式约束及不等式约束。等式约束为潮流平衡约束,不等式约束为电压及功率因数约束。分析约束条件,凡是潮流计算结果收敛均能满足等式约束,故将不等式约束转化为惩罚因子,从而将受限型目标函数转化为非受限型,即: 式中:UDG_max,UDG_min分别为所有光伏并网节点中t 时刻电压最大值和最小值;Umax,Umin分别为节点电压允许上、下限值。 本文利用粒子群优化算法求解目标函数。主要步骤如下。 步骤1:输入配电系统模型及目标函数。 步骤2:输入粒子群算法控制参数包括粒子数量N、迭代次数I、惯性权重、加速权重等。 步骤3:随机创建初始粒子,每个粒子是由所有光伏有功、无功构成的数组,其被视为目标函数的一个解,选出全局初始最优Pd和Pi,d每个粒子i 的个体最优解Pi,d。 步骤4:对每个粒子,通过式(12)计算各粒子速度,此后利用式(13)更新粒子位置,重新统计Pd和Pi,d,迭代次数n=n+1; 式中:w 惯性权重;φp,φg为加速权重;rp,rg为随机数。 步骤5:若n 考虑到粒子群优化算法存在一定的不确定性,结果通常会受迭代次数、粒子群规模等因素影响。在实际使用时,需要多次运行,方能确定算法的理想参数,最终得出近似最优解。 本节通过Python 程序语言实现上述相关算法,利用IEEE 33 配电模型,如图4 所示,进行仿真测试。 图4 IEEE 33 配电模型 首先同时在配电系统前、中、后段(节点3,11,20)各选取一个位置接入光伏,通过改变其容量,分析不同方案下电压分布,具体接入方案如表1 所示。得出电压分布曲线如图5 所示。 表1 光伏接入方案 根据图5,随着接入容量的增大,光伏将向上游负荷提供功率,出现逆向潮流,在光伏上游馈线出现电压上升,相对无光伏接入时,无论接入容量大小,均能够提升接入点电压. 图5 接入光伏后节点电压分布 根据图6,依次在节点2,5,15,20 接入容量为3 MW 的光伏。由图6 可以看出,相同容量的光伏接入主馈线不同位置时,其稳态电压分布存在较大的差异。当位置选取不当,如节点15,因接入点出现极大电压导致部分节点电压越上限。 图6 大容量光伏单点接入后电压分布 本节利用2.2 节的方法估算光伏接入后的节点电压,并与牛顿-拉夫逊潮流计算结果比较,限于篇幅只比对光伏接入点电压。首先求得4.1节负荷条件下配电系统的电压灵敏度矩阵,图4配电系统由1 个平衡节点和32 个P-Q 节点构成,无P-V 节点,故灵敏度矩阵为32×32 方阵。在节点3,16,20 接入1 MW 光伏后,节点16 的电压增量为: 表2 灵敏度电压估算法误差 观察表2,2 种方法灵敏度估算误差最大为0.51%,在可接受的范围。 选取接入光伏位置为节点3,16,20 断面。针对低谷负荷,设置光伏不参与调压,场景数20 000 次,渗透率区间为5%,设置配电系统允许的最低电压合格率、网损率、最高容载比分别为90%,85%,65%。 利用蒙特卡洛法统计各区间出现电压及线损越限场景的频次,得出低谷负荷时电压及网损越限频率,如图7—9 所示。低谷负荷时,当光伏渗透率区间为[155%,160%]时,电压越限场景的频率高于10%,渗透率区间为[100%,105%]时,网损超标场景频率高于10%,渗透率区间为[225%,230%]时,容载比超标场景频率高于10%。综合3类指标,得出低谷时,配电系统允许的最大渗透率为105%。配电系统低谷总有功负荷为1.857 MW,得出最大安全接入容量为1.95 MW。同理,可确定高峰条件下安全接入容量。 图7 电压越限频谱 图8 网损越限频谱 图9 容载比越限频谱 在时间序列上,测试第3.2 节给出的P-Q 协同控制算法,时序间隔为小时。保持与4.3 节光伏接入断面一致,分别在3 个节点光伏最大容量均为3 MW,给定MPPT 曲线,运行P-Q 协同控算法,得出各光伏的有功、无功控制曲线如图10所示。 图10 各光伏的功率控制曲线 从图10 中可以看出,运行P-Q 协同控制可将并网点电压控制于合理区间。同时在光伏MPPT 有功功率较大时,实际有功功率均有不同程度消减,节点16 削减率最高,超过50%,弃光情况较为严重,间接说明评估配电系统光伏消纳能力的必要性。 本文首先推导了节点电压稳定裕度因子,根据该因子可知,光伏的接入将在一定程度提升并网点的电压支撑能力。与以往基于蒙特卡洛光伏消纳评估方法相比,本文作出以下改进:引入了基于电压敏感度及网损敏感度的电压、网损估算方法,同时给出电压敏感度的数值计算方法,有效降低计算开销;提出光伏参与调压的评估方法。针对运行中的过电压,提出基于有功-无功协同的电压控制方法,尽可能保证光伏有功最大化、无功最小化,该方法将电压控制转化为求解目标函数最优解的问题,并通过粒子群优化求解该问题。该方法的不足之处在于通过粒子群优化通常只能求得局部最优,同时耗时较长,因此,研究快速、稳定的并网点电压控制方法将是今后工作的重点。3 基于有功-无功协同的并网点电压控制方法
3.1 逆变器工作模式及调压能力分析


3.2 有功-无功协同电压控制



4 仿真测试
4.1 过电压仿真



4.2 电压敏感度误差计算


4.3 蒙特卡洛模拟

4.4 P-Q 控制算法测试


5 结语
