基于自适应遗传量子粒子群算法的配电网故障定位
2021-07-16杨洪杰张尚德赵梦琪
宫 宇,张 莲,2,杨洪杰,李 涛,贾 浩,张尚德,赵梦琪
(1.重庆理工大学 电气与电子工程学院,重庆 400054;2.重庆市能源互联网工程技术研究中心,重庆 400054)
0 引言
随着配电网的不断发展壮大,对配电网的故障定位提出了更高的要求。因此亟需一种同时具有高准确性和快速性的故障定位新方法[1]。
目前,配电网故障定位主要存在以下问题:配电网规模不断扩大,其结构及网络的潮流变得更加复杂;由于收集故障电流信息的FTU(馈线终端单元)受自然环境或电磁等因素的影响,可能会导致其获取的信息发生缺失或畸变;现阶段的配电网规模很大,其对应的故障信息维度较高,导致求解过程的计算量过大。因此以PSO(粒子群算法)为首的人工智能算法成为配电网故障定位的主流方法,其主要包括遗传算法、人工蚁群算法、PSO、免疫算法等。如文献[2]提出了一种基于图论知识的改进矩阵算法来进行配电网故障定位,该算法虽然可对单重和多重故障定位,但是当存在故障信息畸变时不能准确判断故障位置。文献[3]将迁移学习和深度卷积神经网络相结合来进行故障定位,此方法虽然不易受过渡电阻、故障类型、噪声等因素影响,但仍需要大量数据来训练神经元。文献[4-6]利用遗传算法解决配电网故障定位问题,能够取得全局最优值,但准确度不高;文献[7-8]分别利用人工蚁群算法和蝙蝠算法来进行配电网故障定位,但对畸变信息的容错率低;文献[9-10]利用免疫算法和粒子群算法进行故障诊断,但当存在故障信息缺失时,不能准确判断故障区段的问题。
PSO 是一种利用记忆与反馈机制实现快速有效搜索的群体智能优化方法,优点在于计算速度快,在解决大规模数学优化问题上有一定的优势[11]。相对于其他智能算法,PSO 具有参数设置比较简单、易于实现、搜索速度快、收敛性好等优势。但是,PSO 在针对有多个局部极值点的函数时,容易发生陷入局部最优的现象,从而导致早熟,寻找不到最优的点[12]。
针对标准PSO 的缺陷,本文提出了QPSO(量子粒子群算法)并对其进行改进,引入GA(遗传算法)的变异及交叉操作,进一步提升算法的全局寻优和局部寻优能力,以克服PSO 的缺点,实现配电网快速而准确的故障定位。
1 AGA-QPSO 的原理
1.1 自适应遗传算法
GA 是由霍兰德教授以基因的自然选择和遗传变异为理论依据,在20 世纪70 年代提出的全局性概率型搜索优化模型[13]。传统的GA 里,交叉概率Pc、变异概率Pm均是一个固定的常数,这对它的寻优性能有很大的影响。因此,本文提出了依据个体适应度值而进行自适应地调整交叉概率、变异概率的AGA(自适应遗传算法),提升其寻优性能。改进后的交叉概率、变异概率如下:
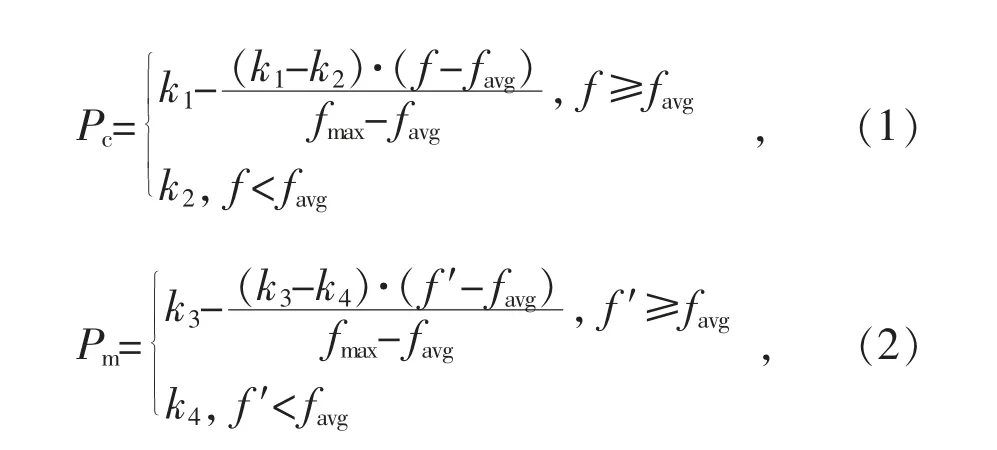
式中:fmax代表种群中最大适应度函数值;favg代表每代种群的平均适应度函数值;f 代表进行交叉操作的2 个个体的适应度值中较大的值;f′代表进行变异操作的个体的适应度函数值;k1=0.9,k2=0.6,k3=0.1,k4=0.01。
1.2 量子粒子群算法
QPSO 作为近年来发展很好的一种智能算法,是由学者Sun 等人于2004 年提出的[14]。其基本原理是在PSO 的基础上通过量子测不准原理来描述各个粒子的运动状态[15]。PSO 通过位置和速度来表达粒子的状态;QPSO 则是利用波函数y(x,t)来表示粒子的状态[16]。波函数是粒子在某处出现的概率分布,表示的是对测量结果的一种估计[17]。QPSO 的运动方程为:

式中:x(t+1)表示粒子当前所在的位置;r 为[0,1]之间的随机数;x(t)为上一时刻粒子的位置;Pi为第i 个粒子的个体最优位置;Gi为第i 个粒子的群体最优位置;φ 表示CE(扩张—收缩因子),其值的大小对粒子的收敛速度有很大的影响,一般情况下,φ<1.781;mbest表示粒子平均最优位置;N 表示粒子群中的粒子数量;α 和u 则分别为[0,1]之间表示均匀分布以及随机分布的常数。
为了更好的提升QPSO 的收敛性,对CE 因子进行了改进,使φ 的取值能够随着迭代次数而线性地减小,使算法在搜索的末期能够进行更好的局部搜索,更加准确地找到最优解[18]。改进后的φ 可表示为:

式中:φmax,φmin分别表示CE 因子的最大值与最小值,通常取值在0.5~2.0 之间;Tmax,t 分别表示最大迭代次数和当前迭代次数。
同时,为了使QPSO 能够解决离散问题,将其进行二进制编码,并改进其粒子平均最优位置的取值,来更好地解决离散化的问题[19]。改进后的公式如下:

式中:avg 表示位置的平均值;pbestj表示最优位置的第j 列的取值;sizepop 表示粒子群种群数量;相应地,mbestj表示的是粒子平均最优位置的第j 列的取值。
1.3 AGA-QPSO
本文根据AGA 及QPSO 的特点,在QPSO 的迭代过程中,通过引入AGA 中能够根据适应度值动态调整变异概率和交叉概率的变异和交叉操作,提出AGA-QPSO。该算法对QPSO 的全局最优位置和最优个体的速度执行变异操作,接着再对执行变异操作之前与变异后粒子的分量进行随机地交叉,这样就得到了新的种群。再进行变异与交叉操作后,种群得到了进化,提升了算法的收敛速度。
2 AGA-QPSO 的故障定位模型及算法流程
当配电网发生故障时,网络中的FTU 就可以检测到故障电流信息,再将故障电流信息上传至SCADA(数据采集与监视控制系统),SCADA中心里的故障定位系统再根据故障电流信息来判定故障区段,最终实现故障的定位[20]。
2.1 故障电流编码
本文采用二进制编码将故障电流信息转化为故障向量。定义故障电流Ij为:

2.2 开关函数的构造
开关函数是根据开关节点处监测到的故障过电流信息和线路区段本身的状态之间的关系而构造的函数,其能够使优化算法更好的利用和分析开关节点处的过电流信息,进而判断出故障节点的位置[21]。
简单配电网如图1 所示。

图1 简单配电网网络
图1 中,G 表示电源模块,1—4 为开关节点,(1)—(4)为各个开关节点的相对应的馈线区段。
本文采用如下的开关函数:

式中:Lj为馈线区段的状态;+表示或运算;M 表示与开关节点下游相关联的所有的区段的集合。
2.3 评价函数的构造
在配电网进行故障定位时,评价函数即为适应度函数,当配电网的系统中馈线区段发生故障时,评价函数由配电网的FTU 根据上传到主站的故障电流信息与构建的开关函数期望值的差值表示[22]。利用评价函数,可以在线路故障信息与开关电流信息之间构成一定的联系,从而确定在进行算法优化求解故障区段时解的优劣程度[23]。本文根据“最小集”的原理来构造评价函数,如式(11)所示:

式中:F(SB)为评价函数值,其值越小,表示准确度越高,因此取极小值;SB表示网络中各个设备的状态值,若设备存在故障则取值为1,若设备正常则取值为0;Ij表示第j 个开关节点上的过电流信息;表示各个开关节点的开关函数的期望状态值;N 表示网络中开关总数;θ 表示权重系数,取值范围为0~1,本文取θ=0.5[24];SB(j)表示各个馈线区段的状态值。
2.4 算法流程
本文算法中的维数代表了网络中区段的数量;粒子的位置则代表评价函数的最优解,即网络中各个区段状态值。其中每个区段的取值为“0”或“1”,“0”表示区段为正常状态,而“1”则表示该区段发生了故障。当故障发生后,算法的具体步骤如下:
(1)构建开关函数与评价函数并对种群进行初始化。
(2)计算评价函数值并确定波函数状态。
(3)计算粒子的平均值和平均最优位置。
(4)计算变异概率并随机选取部分粒子进行变异。
(5)计算交叉概率并对变异后的粒子位置和速度分量执行随机地交叉操作。
(6)比较粒子当前位置和评价函数值并更新。
(7)判断是否达到最大迭代次数或收敛精度,若未达到则返回步骤(3);若达到则进行下一步。
(8)输出种群最优位置即评价函数最优解,从而判断出故障区段。
算法的流程如图2 所示。

图2 AGA-QPSO 的配电网故障定位流程
3 算例仿真
本文以图3 所示33 节点配电网进行仿真测试。其中G 为系统电源,1—33 为开关节点,(1)—(33)为各个开关节点对应的馈线区段。

图3 33 节点配电网网络
3.1 算例仿真分析
3.1.1 单重故障测试
假设在单个不同馈线区段发生故障,在故障信息完备的情况下进行测试。测试结果见表1。

表1 单重故障测试结果
由表1 可知,当单一的区段发生短路故障时,无论故障发生在任一区段,改进算法均能准确判断故障区段。
3.1.2 多重故障测试
假设在多个不同的馈线区段发生故障,在故障信息完备的情况下进行测试。测试结果如表2所示。

表2 多重故障测试结果
由表2 可知,当多个馈线区段同时发生短路故障时,改进算法仍然能够准确地定位故障位置。
3.1.3 信息缺失测试
在实际的配电网中,FTU 常常装设在室外,容易受到外界复杂环境的影响,致使FTU 上传信息出现缺失或漏报的情况。
假设在单个或多个不同的馈线区段发生故障,在故障电流信息缺失或漏报的情况下进行测试。测试结果如表3 所示。

表3 信息缺失测试结果
由表3 可知,无论是单一区段或者多个区段同时发生故障且存在不同程度的电流信息缺失时,本文所提的改进算法均能很好的诊断出发生故障的区段,具有较高的容错率。
3.2 算法对比分析
为了突出AGA-QPSO 在故障定位中的优势,本文在此将改进算法与AGA 以及IBPSO(带压缩因子和线性递减惯性权重的改进粒子群算法)在不同故障类型下的算法性能进行对比。
3.2.1 快速性对比分析
针对不同的故障类型,即故障信息完备时单一区段发生故障、多个区段发生故障以及存在故障信息漏报或缺失的单一区段发生故障、多个区段发生故障,来进行算法准确性、快速性的对比分析。AGA,IBPSO,AGA-QPSO 3 种算法的迭代曲线如图3 所示。
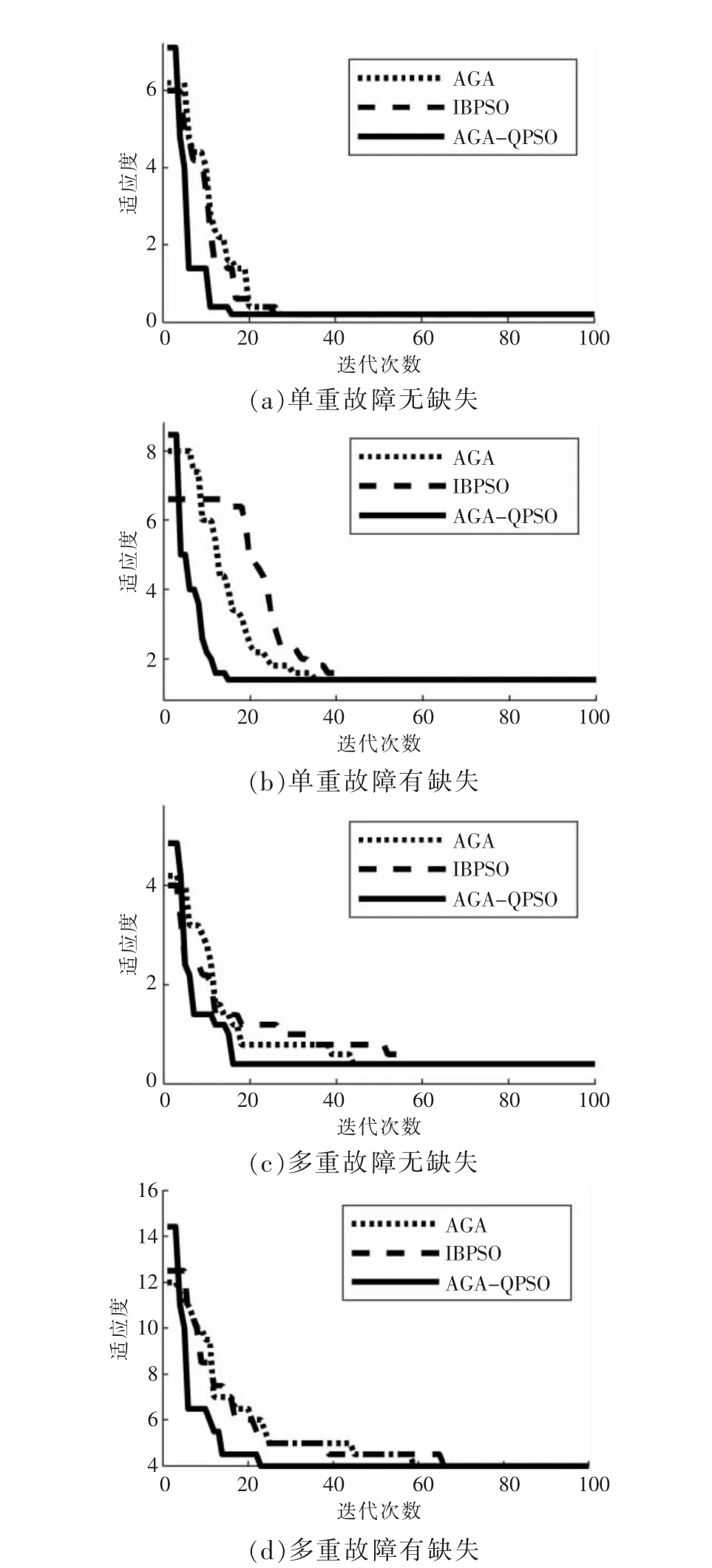
图4 不同故障类型的AGA,IBPSO,AGA-QPSO算法迭代曲线对比
预设区段(13)发生故障且无故障信息缺失,区段(13)发生故障且节点5,7,12 故障信息缺失,区段(14)和(27)发生故障且无故障信息缺失,区段(14)和(27)发生故障且节点4,8,11 故障信息缺失,分别对应图3(a)—图3(d)。由图3 可知,随着故障区段的增加以及故障信息缺失的出现,AGA 和IBPSO 迭代次数明显增加;而AGAQPSO 能够克服故障区段的增加以及故障信息缺失的出现所带来的影响,能够快速地定位故障位置,具有一定的容错性。
3.2.2 准确性对比分析
以图3 中4 种故障情况为算例,分别对3 种算法进行50 次仿真测试,进一步进行准确性对比,3 种算法的仿真结果如表4 所示。

表4 3 种算法准确率对比
通过表4 的准确率对比,可以看出,AGA 和IBPSO 对于多个区段发生故障且存在大量故障畸变的情况,准确率不高,对畸变故障信息容错性较差;AGA-QPSO 在多个区段发生故障时,有较高的定位准确率,且对于畸变的故障信息具有较高的容错性。
4 结语
本文利用AGA-QPSO 来进行配电网故障定位,通过仿真分析,验证了算法的可行性。在故障信息完备以及部分故障信息缺失情况下,对单重故障和多重故障进行了仿真测试,仿真结果表明混合算法能够准确地判断配电网故障区段。通过3 种算法的迭代次数和准确率对比,得出了本文改进算法收敛速度更快,准确度更高的优势,同时对于畸变信息具有更高的容错性。
但本文所提方法仍具有一定局限性,当节点增加或者分布式电源接入配电网后,配电网的结构和潮流会变得更加复杂。以及对于架空、电缆等混合网络,该方法不再适用,将在后续的过程进行进一步研究和改善,扩大其适用性。
