Mobius 函数在古典筛法上的应用

邓从政

（凯里学院，贵州凯里 556011）

0 引言

素数是数论中被研究最广泛的一类数，除在同余理论、整除理论、不定方程理论及指数和原根这些基础问题经常用到之外，在密码学和编码学上也有广泛地应用，如椭圆曲线密码、RSA 密码、圆锥曲线密码三大公钥密码体制的加密和解密都依赖于大素数［1］.长期以来找出一个大整数范围内的所有素数是数论中被研究最广泛的一个课题，其中素数的数量、素数的分布、素数表的构造都依赖于现存找到的素数，古典筛法可以找出不超出给定的一个正整数范围内的所有素数，而且十分有效，它是构造素数表的一个实用方法［2］.本文通过Mobius函数及其独特性质从理论上证明古典筛法的有效性，为寻找素数提供一个简洁而实用的算法.

1 古典筛法原理

1.1 算术基本定理

一个不等于1 的正整数不是合数就是素数，素数只有1 和它本身两个素因数，而合数除了这两个因数之外还有其他的真因数，那么怎样把任意一个整数进行因数分解呢?对此我们有下面的唯一分解定理即算术基本定理［3］.

定理1（算术基本定理）设整数a≥2，那么a一定可表为若干素数的乘积，即a=p1p2...ps，其中pj(1 ≤j≤s)是素数，且在不计次序的意义下上述表法是唯一的.

推理1设整数a≥2，那么a一定可表为若干素数的乘积，即其中pj(1 ≤j≤s)是素数，且在不计次序的意义下上述表法是唯一的.

根据上述算术基本定理，我们可以得到一个寻找素数的算法，即古典筛法，也叫Eratosthenes筛法.再由最小自然数原理取p=min{p1,p2,···,ps}，则，这就是一切筛法的原理.

推理2设整数a≥2，那么a一定可表为若干素数的乘积，即a=p1p2...ps，其中pj(1 ≤j≤s)是素数，则必有素数p|a且满足

特别地，我们取s=2，这就是古典筛法的原理.

推理3设整数a≥2，则必有素数p|a且满足

1.2 古典筛法的算法与应用

根据筛法原理，理论上我们可以找出任意大整数范围内的所有素数，从而找出所有的素数，古典筛法就是把大整数分段去倍来寻找素数的，比如我们要找出[1,n]范围内的素数，其算法如下：

（3）删除1和[1,n]范围内所有p的倍数ps≤n；

（4）删除以上倍数后剩余的数即为所求的素数.

案例用古典筛法找出不超过300的所有素数.

（2）找出[1,17]范围内的所有素数：2，3，5，7，11，13，17；

（3）删除1和[1,300]范围内所有2，3，5，7，11，13，17的倍数；

（4）删除以上倍数后剩余的数为：2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97，101，103，107，109，113，127，131，137，139，149，151，157，163，167，173，179，181，191，193，197，199，211，223227，229，233，239，241，251，257，263，269，271，277，281，283，293.

剩余的数即是[1,300]范围内所有素数，并可由此出发，可以筛出[1,3002]，[1,(3002)2]，…，[1,3002k]，更进一步可以利用这种筛法构造出素数表.那么当整数充分大时这张素数表上的素数有多少个，其分布是否有一定的规律呢?下面介绍一个著名的数论函数在古典筛法上的应用，并从理论上证明古典筛法的有效性和实用性.

2 Mobius函数及其独特性质

以符号π(x)表示不超过实数x的素数个数，以2=p1＜p2＜···＜ps表示所有不超过的素数，则有根据上述筛法我们可以把1 ≤n≤x的所有整数n中能被任一pi(1 ≤i≤s)整除的数除掉后，剩下的就是满足条件的全部素数p和1，所以剩下的数的个数为下面我们探讨能否用一个公式来表达这个式子.

在[1,x]上的正整数n能被d整除的数的个数为这样能被取定的素数pi(1 ≤i≤s)整除的数的个数是被2个取定的不同的整除的数的个数是被r个两两不同的整除的数的个数是如果设则显然有G≤T.

上式右边表示依次把区间[1,x]上的[x]个正整数中能被p1整除的个整数去掉，被p2整除的个整数去掉，一直到把被ps整除的个整数去掉后剩下的整数个数，显然那些在[1,x]上恰好只能被一个整除的整数也就是形式的数，在这个过程中无重复的每一个数被去掉了一次，而对那些在[1,x]上的恰好只能被r(2 ≤r≤s)个两两不同的整除的整数，即形如的数在这个过程中恰好每个数被重复的去掉了r次，所以上式成立.那么这个差值是什么呢?对给定的r，考察量它是表示对满足以下条件的在[1,x]上的正整数n的个数的某种有重复的计数：恰好被r个两两不同的整除的n恰好被计算了一次，恰好被t(r＜t≤)个两两不同的整除的n恰好被重复地计算了次.如果为了弥补G去掉了过多而加上V2，则需要考虑量

由此可得：

上述证明从略，详见文献［1］，若记Tr=[x]-Ur,1 ≤r≤s，则综上可得如下系列结论.

定理2在上述条件和符号下，我们有［3-4］：（i）Us是区间[1,x]上与p1p2...ps不既约的整数n的个数，即满足1 ≤n≤x,(n,p1p2...ps)＞1 的n的个数；（ii）Ts是区间[1,x]上与p1p2...ps既约的整数n的 个 数，即 满 足1 ≤n≤x,(n,p1p2...ps)=1 的n的 个 数；（iii），或事实上，这就是容斥原理对这个问题的精确阐述，同时更一般地推广了古典筛法，也就是广义筛法，即对给定的序列A及整数K，如何求出序列A中所有与K既约的整数个数，对此有如下结论［4］.

定理3设A是一个给定的有限整数序列，K是给定的正整数，设Ad表示A中被正整数d整除的所有整数组成的子序列，p1,p2,...,ps是K的所有的不同的素因数，以及表示序列Ad中的整数个数，那么序列A中所有与K既约的数的个数为

特别地，如果A是由1,2,···,[x]组成的序列，K=p1p2...ps,p1,p2,...,ps是不超过的全部素数，这时有

这个表达式要利用K的全部素因数，式子有些繁琐，下面我们引入Mobius 函数，它可以简化上面的公式，并且可以直接简单的证明上述广义筛法原理.

定义（Mobiu函数）设变数d取正整数，p1,p2,...,pr是两两不同的素数，μ(d)定义为

下面介绍Mobius函数一个最基本最重要最漂亮的性质［3，5］.

定理4设n是正整数，我们有，当n=1 时结论显然成立.设n=，由定理4可知

3 Mobius函数在古典筛法上的应用

根据Mobius函数的基本性质，我们可以很容易很简洁的证明古典筛法及广义筛法的正确性，下面我们来看看其在筛法上的妙用.

定理5（筛法原理）

证明

下面我们利用Mobius 函数的基本性质来给出π(x)的一个漂亮的上界估计，对此先证明如下一个引理.

引理6设x≥y≥2,φ(x,y)表示不超过x且其素因数都大于y的所有正整数的个数，那么有

定理6（上界定理）设x≥10.pn表示第n个素数，则一定存在正常数c使得

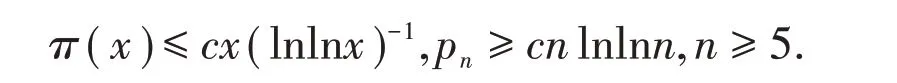
证明由定理6 可知，π(x)-π(y)=φ(x,y),2 ≤x≤y，从而有

现取y=lnx,则可得π(x)≤x(lnlnx)-1+lnx+2lnx≤x(lnlnx)-1+x0.7+lnx≤cx(lnlnx)-1.特别的，如果取x=pn,由上知道π(pn)=n,pn＞n，故可得出pn≥cnlnlnn,n≥5.

4 结束语

Mobius函数是一个重要的数论函数，它有许多极其独特的性质，可以给出欧拉函数的简洁证明，还给容斥原理提出了一个逻辑上清晰易懂的推理和阐述.本文应用其性质从理论上证明了广义筛法及古典筛法的正确性和有效性，为寻找素数和构造素数表提供一个简洁而实用的算法［7］，并给出了一个较精确的漂亮的上界估计，在理论上和实践中都具有极其重要的价值.