圆弧形模切刀折弯成形的工艺方法
2021-07-16胡志超王云超林荣川郑添义
胡志超,易 燕,王云超,林荣川,郑添义
(1.集美大学海洋装备与机械工程学院,福建 厦门 361021;2.集美大学计算机工程学院,福建 厦门 361021)
0 引言
模压加工是印刷、包装产品后期加工的重要工艺手段。模压工艺所使用的模切压痕版由模切刀或压痕刀(为叙述方便,下文简称为模切刀)压入木基刀模底板装刀缝组装而成。刀线图是模切刀在数控弯刀机上折弯成形的加工图,对于圆弧形模切刀刀线图,需先对其进行线性化工艺处理,以多段线拟合圆弧。圆弧等分的段数、等分线段长度以及相邻线段间的夹角(分别对应弯刀加工的折弯次数、进刀长度、折弯角度)对模切刀的加工精度、组装精度以及模切刀折弯加工的效率存在直接影响,并最终影响模切产品的质量。目前生产中采用调机试验方法,以一系列半径的90°包角圆弧为测试对象,先根据经验指定其折弯次数,再计算获得进刀长度及折弯角度,以组装成功作为折弯精度满足要求的判据,通过多次的折弯加工及组装测试,不断对进刀长度和折弯角度进行人为补偿以修正,最终获得指定折弯次数条件下的三参数值,并保存于数据库。实际模切刀折弯加工时,根据圆弧形模切刀加工半径及包角对数据库查询、插值确定上述三参数[1-2]。该经验数据工艺法存在以下不足:
1)理论计算的进刀长度和折弯角度存在圆整误差,当折弯次数较大时,圆整误差必将对模切刀精度产生较大影响;
2)测试人员凭经验取值,缺乏理论依据,不一定是权衡精度与加工效率后的最佳值;
3)试验重复次数多,耗时耗材。
鉴于此,本文通过对圆弧形模切刀进刀长度的理论分析,建立了进刀长度的理论计算公式,分析了折弯加工中弯刀机进刀系统和弯刀系统圆整误差的影响。在此基础上,针对大弧长、小弧长圆弧形模切刀的不同加工及组装特点,提出了选整长度圆整角度、选整角度圆整长度两种工艺方法。最后,基于AutoCAD 2010平台及其二次开发软件包ObjectARX 2010,开发了数控弯刀机CAD/CAM系统,通过圆弧折弯成形实验,验证了该工艺方法。
1 圆弧形模切刀折弯成形原理
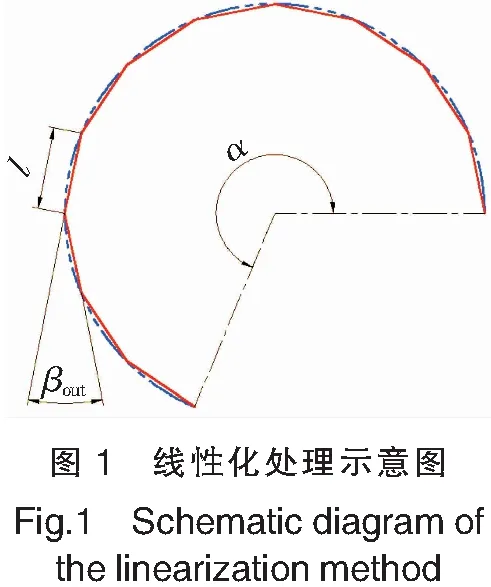
圆弧形模切刀线性化工艺处理示意图如图1所示。其中:双点划线为原模切刀刀线图,实线为线性化处理后对应的刀线图;α为包角;l为进刀长度(即等分线段长度);βout为实际折弯角。
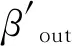
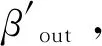
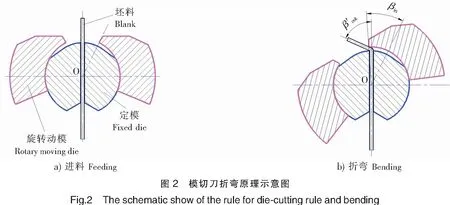
2 进刀长度的理论分析及计算
刀模底板一般采用木材为基材,圆弧形模切刀通过压力组装入底板装刀缝时,装刀缝具有一定的变形量。对于相同半径的圆弧形模切刀,n、l、βout取值不同,模切刀与装刀缝之间的组装位置关系也不相同。通过对模切刀与装刀缝之间不同组装状态的分析,本文提出了理想组装和极限组装两种特殊的组装状态,在此基础上进行进刀长度的理论分析及计算。
2.1 计算模型简化的约定
1)忽略木板由于温差变化等原因所产生的变形。
2)考虑刀片厚度尺寸较小(常用刀片厚度0.71 mm),将坯料展开,所在中性层简化至几何中心[4]。
3)折弯角圆弧半径理论计算是比较困难的,只能在折弯后测量获得,或在此基础上建立经验公式[5-6]。考虑到实际生产中折弯角圆弧测量的不便以及折弯角圆弧半径较小、圆弧包角较大,建模计算时忽略折弯圆角[7]。值得说明的是,折弯角圆弧的简化只对进刀长度的理论计算值产生微量影响,不会产生模切刀加工时进刀长度误差。
4)进刀长度l所对应的模切刀直线段长度较短,通常在2 mm以内,通过压力装入刀模底板装刀缝时,可认为各直线段模切刀不产生弯曲变形。
2.2 理想组装状态下最大进刀长度分析及计算
本文所指理想组装状态,指模切刀组装入底板装刀缝后,模切刀几何中心线内切于变形前的刀模底板装刀缝圆弧中心线(对应刀线图)。
理想组装条件下允许的最大进刀长度的示意图如图3所示。其中,剖面线区域表示厚度为t的模切刀,剖面区域中心的点划线为模切刀几何中心线;点划线圆弧表示变形前的刀模底板装刀缝几何中心;两实线圆弧表示通过给定组装压力将模切刀装入刀模底板,装刀缝变形后的内外轮廓线;双点划线圆弧表示在给定组装压力下装刀缝产生最大变形量时外轮廓线对应的极限位置。在理想组装条件下取最大进刀长度时,装刀缝的内轮廓线对应给定组装压力下内轮廓最大变形量的极限位置。Δ值对应给定组装压力下装刀缝产生最大变形后的宽度值,该Δ值由经验或试验测量确定。
由图3可计算出理想组装条件下最大进刀长度:
(1)
2.3 极限组装状态下最大进刀长度分析及计算
本文所指极限组装状态为:模切刀组装入底板刀缝后,在给定组装压力条件下装刀缝产生最大变形量的组装关系。
如图4所示,极限组装状态下的最大进刀长度为lmax,其余各符号及图线意义与图3相同。与图3不同之处在于,模切刀组装入装刀缝后,装刀缝达到最大变形量。
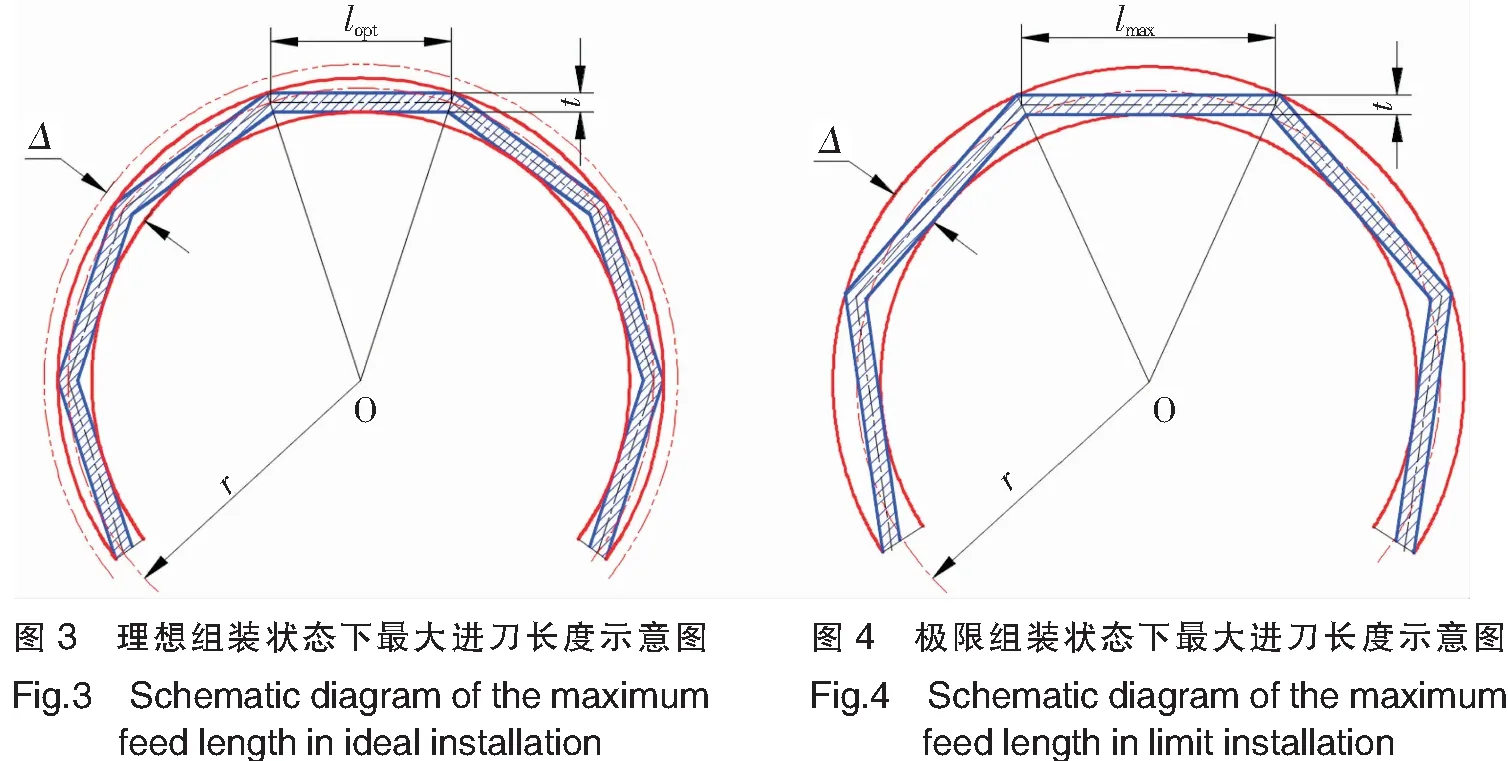
由图4可计算出极限组装条件下最大进刀长度:
lmax=(2r+t-Δ)tan[arccos(2(r+t)-Δ/2r+Δ)]。
(2)
3 圆弧形模切刀加工误差分析及工艺处理方法
3.1 模切刀的加工误差分析
模切刀的数控加工误差有编程误差、进刀及弯刀系统误差、进刀及弯刀对零误差等。其中,后两者由弯刀机中各机械零部件加工、装配及参数设置等因素产生,模切刀的加工工艺方法与之无直接关系。编程误差由逼近误差、圆整误差组成。逼近误差是指圆弧线性化处理后的线性长度与原圆弧长度之间的误差;圆整误差是指数控系统在对进刀长度和折弯角的理论计算值进行数据处理时,四舍五入圆整为整数倍的脉冲当量值而产生的误差[8-9]。圆弧形模切刀的不同工艺处理方法,所产生的逼近误差和圆整误差也不相同。
由式(1)、式(2)计算得到的最大进刀长度为约束上限,可为逼近误差达到组装精度要求提供理论依据和保证。
目前在圆弧形模切刀线性化工艺处理方法中,所获得的l及βout理论计算值一般含多位小数,甚至为无理数,在圆整数据处理过程中,两者都因四舍五入产生误差。设进刀脉冲当量为δfm,弯刀脉冲当量为δbm, 则单次进刀的最大圆整误差为δfm/2,单次弯刀的最大圆整误差为δbm/2[10]。圆弧形模切刀通过n-1次折弯成形后,总的进刀圆整误差和弯刀圆整误差分别为nδfm/2、(n-1)δbm/2。可见,当段数n值较大时,进刀圆整误差及弯刀圆整误差也较大,势必对模切刀的加工质量及其组装产生影响,导致调机测试次数增加。
3.2 圆弧形模切刀的工艺处理方法
不同弧长的圆弧形模切刀组装及加工特点分析如下:
1)对于大弧长圆弧形模切刀,由于其弹性变形量大,变形容易,所以压入刀模底板装刀缝时,允许存在较大的折弯角误差;
2)对于小弧长圆弧形模切刀,由于其弹性变形量小,变形困难,所以压入装刀缝时,允许存在的折弯角误差较小;
3)圆弧形模切刀折弯加工所产生的长度误差与单次进刀误差以及进刀次数直接相关,属于单次进刀误差的累积,小弧长圆弧形模切刀进刀次数少,长度误差小;大弧长圆弧形模切刀进刀次数多,则长度误差大。
根据以上特点分析,以长度最大允许误差为判据,将圆弧形模切刀划分为大弧长、小弧长两种类型,对两种类型模切刀设计不同的线性化工艺处理方法。对于大弧长圆弧形模切刀,采用选整长度圆整角度的工艺处理方法;对于小弧长圆弧形模切刀,采用选整角度圆整长度的工艺处理方法。具体分析及处理过程如下。
1)根据圆弧半径r、刀片厚度t、底板装刀缝最大变形量后的宽度值Δ,计算理想组装条件下最大进刀长度lopt、极限组装条件下最大进刀长度lmax;根据模压产品的形状精度等级要求不同,选用lopt或lmax值作为进刀长度最大参考值。
2)以进刀脉冲当量δfm为基本单位,对lopt或lmax进行取整,获得脉冲当量整数倍的参考进刀长度:
lref=[floor(lopt/δfm)-m]×δfm;
(3)
或
lref=[floor(lmax/δfm)-k]×δfm。
(4)
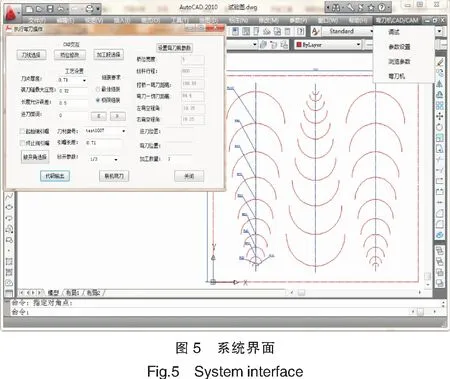
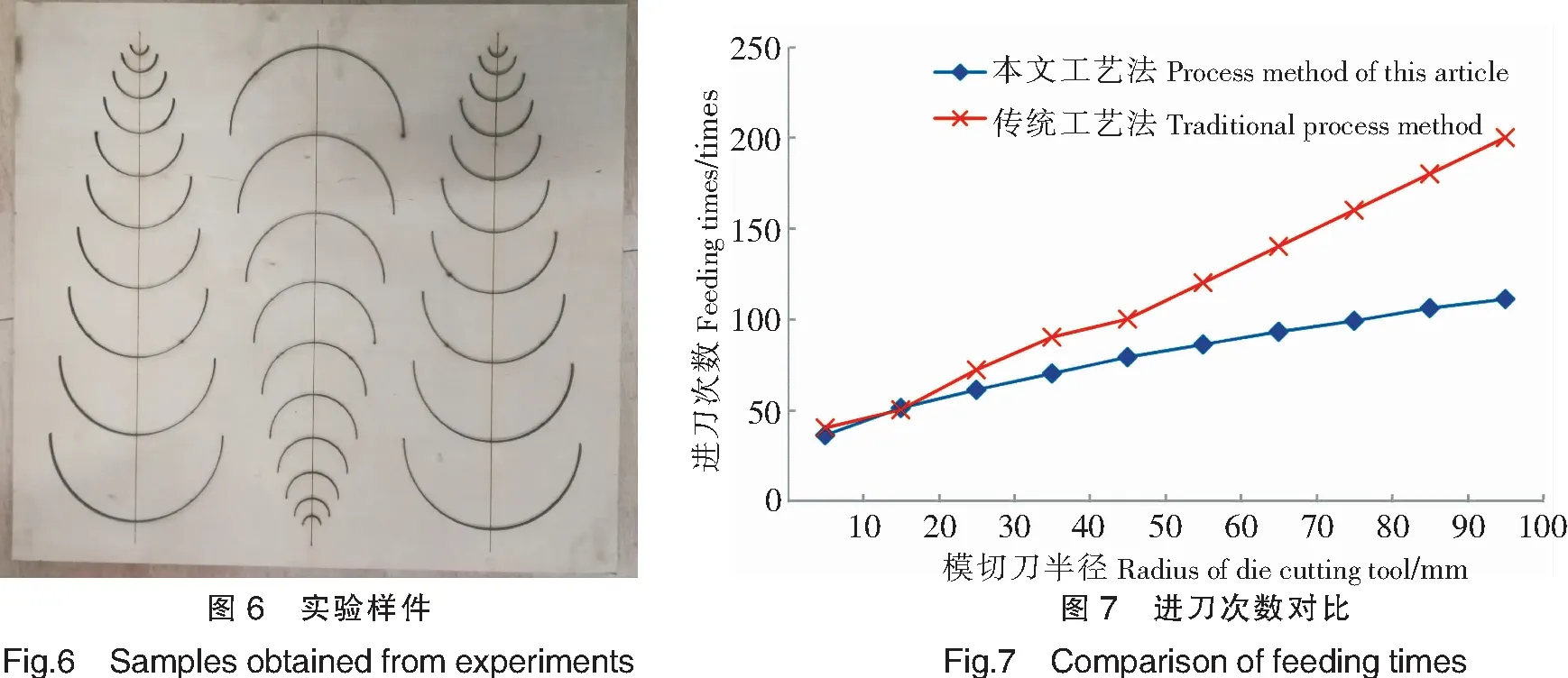
其中:floor表示取不大于该值的最大整数(下同);m、k为不小于0的整数,且m 3)根据圆弧半径r、圆弧包角α及参考进刀长度lref,计算进刀次数: n=ceil[α/(2arcsin(lref/2r))]。 (5) 其中,ceil表示取不小于该值的最大整数(下同)。 4)根据单次进刀最大圆整误差δfm/2,由式(5)可得该圆弧形模切刀的最大进刀长度圆整误差: δlr=ceil[α/(2arcsin(lref/2r))]×(δfm/2)。 (6) 根据模切刀实际加工及组装过程中的长度误差要求,设置长度允许最大误差为δlmax,长度加工误差为δl,考虑逼近误差由极限长度及底板装刀缝变形所容纳,取δlr=δl/10[11]。当δl>δlmax,即δlr>δlmax/10时,定义该圆弧形模切刀为大弧长圆弧形模切刀;当δlr≤δlmax/10时,定义该圆弧形模切刀为小弧长圆弧形模切刀。大弧长圆弧模切刀的长度误差超差,需减小或消除其长度圆整误差。 5)对于大弧长圆弧形模切刀,取进刀长度为lref,即先设置进刀长度为取整后的参考长度,则前n-1次进刀长度ln-1=lref,前n-2次弯刀的折弯角βout_n-2=2arcsin(lref/2r);第n-1次弯刀的折弯角βout_n-1=α-(n-2)βout_n-1,第n次进刀长度ln=2rsin(βout_n-1/2)。整段圆弧形模切刀由l定距等分,前n-1次无圆整误差,第n次进刀长度ln≤lref,最多存在一次进刀圆整误差δfm/2,整段圆弧形模切刀基本消除圆整误差,极大减少了长度加工误差。由折弯角βout_n-2、βout_n-1及“折弯角-驱动角关系表”查询或插值计算获得加工所需弯刀驱动角βin_n-2、βin_n-1,并由数控程序对其圆整。单次弯刀驱动角产生δbm/2的最大圆整误差,整段圆弧产生(n-1)×δbm/2的驱动角圆整误差,由此而产生相应的折弯角误差。虽然该折弯角误差较大(因n-1表示的折弯次数值较大),但可以利用大弧长圆弧形模切刀组装时的大弹性变形来弥补。 6)对于小弧长圆弧形模切刀,先取计算折弯角βcal_out=α/n,再由βcal_out及“折弯角-驱动角关系表”查询或插值计算获得弯刀驱动角βcal_in。以弯刀脉冲当量δbm为基本单位,取整获得加工所需弯刀驱动角βin=floor(βcal_in/δbm)δbm,再采用文献[3]的方法,由βin获得实际折弯角βout,最后计算出实际的进刀次数n=ceil(α/βout)、前n-1次进刀长度ln-1=2rsin(βout/2)、第n次进刀长度ln=2rsin(α-(n-1)βout/2)。βin为计算后的取整值,无折弯驱动角圆整误差,能满足小弧长圆弧形模切刀折弯角的组装要求;l由数控程序进行圆整,单次进刀产生δfm/2的最大进刀长度圆整误差,整段圆弧形模切刀产生n×(δfm/2)的长度圆整误差。因小弧长圆弧形模切刀进给次数n较小,能满足长度加工误差要求。 本工艺算法实现过程如下。 Step1:初始化模切刀片厚度t、装刀缝最大变形量后宽度Δ,读取CAD图中圆弧模切刀半径r。 Step2:根据模压产品的形状精度等级高低不同,选用式(1)、式(3)或者式(2)、式(4)计算并取整参考进给长度lref。 Step3:根据式(5)计算进刀次数n;根据单次进刀最大圆整误差为δfm/2及式(6)计算最大进刀长度圆整误差δlr。 Step4:设置长度允许最大误差δlmax,判断δlr是否大于δlmax/10,若是,按大弧长圆弧形模切刀处理,执行步骤5,若否,按小弧长圆弧形模切刀处理,执行步骤7。 Step5:取前n-1次进刀长度ln-1=lref,前n-2次弯刀的折弯角βout_n-2=2arcsin(lref/2r)。取第n-1次弯刀的折弯角βout_n-1=α-(n-2)βout_n-1,第n次进刀长度ln=2rsin(βout_n-1/2)。 Step6:根据βout_n-2、βout_n-1及“折弯角-驱动角关系表”获得驱动角βin_n-2、βin_n-1,输出大弧长圆弧形模切刀工艺参数n、ln-1、ln、βin_n-2、βin_n-1,工艺算法结束。 Step7:由βcal_out=α/n及“折弯角-驱动角关系表”获得弯刀驱动角βcal_in,根据弯刀脉冲当量δbm取整弯刀驱动角βin=floor(βcal_in/δbm)δbm,再根据“折弯角-驱动角关系表”获得实际折弯角βout。取实际的进刀次数n=ceil(α/βout)、前n-1次进刀长度ln-1=2rsin(βout/2)、第n次进刀长度ln=2rsin((α-(n-1)βout)/2)。 Step8:输出小弧长圆弧形模切刀工艺参数n、ln-1、ln、βin,工艺算法结束。 以上述工艺方法为基础,基于AutoCAD 2010平台及其二次开发软件包ObjectARX 2010,开发了数控弯刀机CAD/CAM系统[12-13],系统主要界面如图 5所示。 通过所开发菜单“弯刀机CAD/CAM”子菜单“弯刀机”调出“执行弯刀操作”无模式对话框,设置刀片厚度0.71 mm、装刀缝最大压宽0.73 mm、长度允许误差0.5 mm等工艺处理参数,其中进刀及弯刀脉冲当量由系统程序读入。实验选用半径10~100 mm范围内10个半圆模切刀为测试对象,以极限组装状态下(选用“极限组装”作为组装要求)的最大极限尺寸(“进刀微调”值取0)为进刀长度,进行了三组折弯实验,并完成了测试模切版的组装,组装一次性成功,达到了模切加工的生产要求,组装后的模切版如图6所示。 传统经验数据工艺法与本文用工艺法折弯成形的进刀次数比较如图7所示。从图7可知,本文工艺法的进刀次数减少明显,且模切刀半径越大,减少越显著,平均折弯加工效率提高25.2%。同时,对于经验比较丰富的技术人员,传统经验数据工艺法一般需3到5次折弯调机测试方能组装成功,本工艺方法可1次折弯、组装合格,显著减少了调机时间和对技术人员的经验依赖。 1)针对实际生产中圆弧形模切刀加工存在的问题,以模切压痕版的组装状态为依据,通过对圆弧形模切刀线性化工艺处理的进刀长度理论分析,提出了理想组装状态下最大进刀长度及极限组装状态下最大进刀长度的概念。在此基础上建立了进刀长度计算公式,为进刀长度的取值提供了理论依据,也为控制圆弧形模切刀折弯加工的逼近误差达到组装精度要求提供了保证。 2)考虑到数控弯刀机进刀系统和弯刀系统圆整误差对圆弧形模切刀折弯成形精度的影响,针对大弧长圆弧形模切刀易变形、折弯段数多以及小弧长圆弧形模切刀难变形、折弯段数少的特点,分别提出了选整长度圆整角度、选整角度圆整长度两种工艺方法。相比传统经验数据工艺法,大弧长圆弧模切刀的长度圆整误差减少至δfm/2以内,小弧长圆弧模切刀的角度圆整误差被完全消除。 3)基于AutoCAD 2010平台开发的数控弯刀机CAD/CAM系统进行了折弯加工及组装测试实验,实验结果表明,与传统经验数据工艺法相比,本文方法平均折弯加工效率提高25.2%,调机测试次数由3~5次减少为1次,验证了所提出的进刀长度理论计算公式及工艺方法的可行性和高效性。4 系统实现及实验验证
5 结论
