基于先验稀疏模型的光谱图像压缩采样检测 *
2021-07-16李潇飞唐意东
李潇飞,唐意东
(1.空军工程大学 航空工程学院,陕西 西安 710038;2.中国人民解放军95607部队,四川 成都 610066)
0 引言
近年来,随着窄带滤光技术和成像光谱技术的快速发展[1-2],光谱成像已经成为发展天基预警卫星新型探测手段的重要方向[3]。光谱图像包含探测场景的空间信息和光谱信息,具有“图谱合一”的特点[4],能够提供丰富详细的物质类别信息,能有效提升天基预警卫星的探测性能,但其庞大的数据量也往往给数据采集和实时处理带来巨大挑战[5]。
面对不断提高的空间分辨率和光谱分辨率,基于压缩感知理论[6-8]的光谱图像压缩采样和解码重构,为更加高效地实现数据采集提供了有效途径。然而,在信号检测、分类、估计和滤波等统计推理任务中,数据采样的最终目的是进行检测或分类决策,信号的精确重构有时十分困难且并非必要,因此可以考虑直接基于压缩采样数据开展相关应用[9-16],以进一步提高数据处理效率。此时,由于压缩采样矩阵满足约束等距条件[17],信号被投影到低维空间,不同样本之间的距离减小,加性噪声的干扰被放大,压缩采样数据的应用精度将受到极大影响。
针对这一问题,本文将压缩信号处理(compressive signal processing,CSP)理论[18]引入光谱图像目标检测,根据先验稀疏模型中待测信号能量分布较集中,噪声能量分布较分散的特点,利用待测信号稀疏表示子空间构造压缩采样矩阵,提出一种基于稀疏模型先验知识的压缩采样检测方法,并对其检测性能进行了分析。
1 压缩采样目标检测模型
根据传统Neyman-Pearson检测模型[19],基于压缩采样的目标检测模型为
(1)

(2)
虚警概率一定时,将式(2)代入检测概率最大的似然比检验并简化可得
(3)
定义基于压缩采样数据的最大似然检测器为
t=yT(ΦΦT)-1Φs,
(4)

(5)
(6)
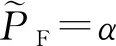
(7)
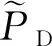
(8)
(9)

(10)
式中:c为较小的正数。结合式(8),(10),可以得到检测概率的理论边界满足:
(11)
引入信噪比定义,可以将式(11)写作
(12)
由于δ值通常较小,因此有
(13)
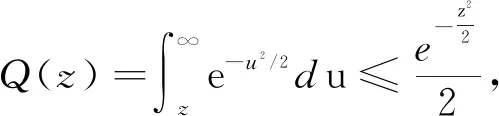


(14)

(15)
由式(15)可以看出,当信号长度L和信噪比SNR一定时,随着测量数目K的增多,检测概率呈指数增长。
2 光谱维非重构压缩采样目标检测
2.1 光谱维压缩采样目标检测模型
在光谱线性混合模型下,可以将基于光谱维压缩采样的目标检测模型描述为
(16)
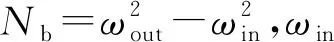
为抑制背景光谱的影响,采用局部正交子空间投影法将压缩采样信号投影到干扰信号Bβ的正交子空间。令Ω=ΦB,构造如下正交投影矩阵
(17)
式中:Ω#=(ΩTΩ)-1ΩT为矩阵Ω的广义逆。假设Ω的奇异值分解为Ω=UΣVT,其中U为矩阵ΩTΩ的特征向量矩阵,即ΩΩT=UΣΣTUT,而V为矩阵ΩTΩ的特征向量矩阵,即ΩTΩ=VΣTΣVT。则背景正交投影矩阵为
I-UΣVT(VΣTΣVT)-1VΣTUT=
I-UUT,
(18)
背景抑制后,检测模型(16)转化为
(19)

(20)
将检测模型写作
(21)
进而可以得到恒虚警条件下的检测概率为
(22)
式中:
ΦT(ΦΦT)-1Φ.
(23)
(24)
2.2 基于稀疏模型先验条件的压缩采样目标检测
模型(19)为光谱压缩采样目标检测提供了一般性方法,尽管利用正交投影矩阵对背景光谱进行了抑制,但由于并未针对待测信号设计采样矩阵,限制了有效信息的获取,导致其检测性能低于传统采样方式,且受目标端元丰度影响较大。为此,本文在模型(19)的基础上,利用待测信号的稀疏表示子空间改进压缩采样矩阵,提出一种基于稀疏模型先验知识的压缩采样检测方法,并对其检测性能进行分析。
假设光谱向量z是变换域Ψ∈RL×L内的k稀疏信号,从Ψ中选取相应的k列原子H∈RL×k,k Φ=G(HTH)-1HT, (25) 式中,G∈RK×k,K≤k为独立同分布随机矩阵,可以得到 (26) 当Ψ为规范正交基时,有HTH=I和zTz=θTHTHθ=θTθ。由于随机矩阵G满足GTG≈KIk和GGT≈kIK,因此有 (27) 采用局部正交子空间投影法进行背景抑制,将式(27)代入式(22),可得检测概率PD满足: (28) 对比式(24),(28)可以发现,检测性能受到光谱混合模型中目标丰度的影响,目标丰度越大,检测性能越好;由于k 实验数据为合成信号,给定一组信号x∈RL,L=1 030,其中20%为噪声信号,即x=n,80%为加噪光谱信号x=s+n。实验中,采用随机高斯矩阵作为采样矩阵,以接收机操作特性(receive operating characteristic,ROC)曲线衡量检测性能。为减小采样矩阵的随机性对检测结果的影响,取100次重复实验的平均检测概率作为最终结果。 图1给出了不考虑光谱混合,信噪比SNR=20 dB,采样率K/L=0.05时的实际检测性能和根据式(13)得到的预测性能。可以看到,不考虑光谱混合时,实际检测性能的上界、下界与预测性能存在较大差异,但其平均值与预测性能十分吻合,重复实验的标准误差在10-4~0.011范围。 图1 无光谱混合时实际ROC曲线与预测ROC曲线Fig.1 Actual ROC and predicted ROC curve without spectral mixing 考虑光谱混合时,给定杂波背景为单一背景光谱,即背景样本B各列向量相同。给定目标端元丰度ρ=0.5,信噪比SNR=20 dB,采样率K/L=0.4,利用背景正交投影矩阵对采样矩阵进行投影,得到图2所示的检测性能和根据式(24)得到的预测性能。对比图2和图1可以看出,尽管采样率从0.05增大到0.4,但由于存在光谱混合,目标端元丰度减小,其检测性能反而明显下降;同时,虽然实际检测性能与预测性能基本吻合,但重复实验误差明显增大,其标准误差增大至0.002~0.097范围。这说明光谱混合对于压缩采样检测影响较大,不仅会降低检测性能,还会削弱压缩采样检测算法的鲁棒性。 图2 有光谱混合时实际ROC曲线与预测ROC曲线Fig.2 Actual detection and prediction of ROC curves with spectral mixing 当具备待测信号先验知识时,给定待测信号训练样本s∈RL,L=1 030,基于离散余弦变换矩阵(discrete cosine transform,DCT)和OMP算法估计其稀疏性,得到如图3所示的稀疏模型。其中,图3a)为DCT变换矩阵;图3c)为稀疏表示系数,稀疏度k=483,此时L/k=2;图3b)为对应的稀疏表示子空间;图3d)为重构结果,其均方根误差为4.487×10-4。 图3 稀疏模型Fig.3 Sparse model 利用稀疏表示子空间构造压缩采样矩阵,得到稀疏模型先验条件下的压缩采样检测结果,如图4所示。对比图2和图4可以看出,改进压缩采样矩阵后,检测性能显著提升,其标准误差也减小至0.001~0.094范围。这说明,利用待测信号的稀疏模型先验知识构造压缩采样矩阵,有助于提升压缩采样检测性能,增强其鲁棒性。 图4 稀疏模型先验条件下的实际ROC曲线与 预测ROC曲线Fig.4 Actual detection and prediction of ROC curves with prior sparse model 为直观比较不同情况的检测性能,并分析采样率对检测性能的影响,以ROC曲线下面积(area under curve,AUC)为性能指标,取目标端元丰度为0.5,信噪比为20 dB,稀疏度为483,得到3种情况下压缩采样检测性能随采样率变化的关系曲线,如图5所示。 图5 不同情况下的AUC值与采样率的关系曲线Fig.5 Relation curve between AUC and sampling rate under different conditions 从图5可以看出,不考虑光谱混合时,检测性能随着采样率的增大而逐渐提升,在采样率增大到0.15时达到峰值,而后保持稳定;另2种情况下,检测性能则始终随着采样率的增大而逐渐提升,但其增长速度随着采样率的增大逐渐放缓,分别在K/L>0.5和K/L=0.4时,达到较高水平并保持稳定。比较3种情况的检测性能发现,考虑光谱混合时,受背景杂波的影响,传统压缩采样检测的性能明显下降,特别是在采样率较低时,其检测性能远低于无光谱混合情况下的检测性能。而利用待测信号的稀疏模型先验知识改进压缩采样矩阵后,其检测性能显著提升。同时,随着采样率的增大,3种情况检测性能之间的差距越来越小,特别是当采样率大于0.4后,稀疏模型先验条件下的压缩采样检测性能十分接近无光谱混合时的检测性能,光谱混合对压缩采样检测的影响被极大削弱。由上述分析可知,在光谱图像压缩采样目标检测中,进行背景抑制和待测信号稀疏特性分析,能够有效提升算法性能。 实验数据为真实光谱图像AVIRIS Indiana Pines[21],将其中占比较少的无线电发射塔作为待检测目标像元,其真实分布如图6所示。 图6 真实光谱图像Fig.6 Indiana Pines 随机选择训练样本,利用DCT矩阵和OMP算法对其稀疏表示模型进行估计,得到其稀疏度为136,光谱重构均方根误差为9.99×10-4。实验2中,分别采用单位采样矩阵、传统随机压缩采样矩阵和经稀疏表示子空间改进后的压缩采样矩阵进行匹配滤波目标检测,以AUC值为性能指标,分析它们在不同采样率K/L下的检测性能,如图7所示。 图7 不同情况下的AUC值与采样率的关系曲线Fig.7 Relation curve between AUC and sampling rate under different conditions 从图7可以看出,由于进行了完全采样,单位采样矩阵对应的AUC值为0.997。而采用压缩采样矩阵时,其检测性能随着采样率的增大而逐渐提升,并且改进后的压缩采样矩阵总能获得较传统压缩采样矩阵更优的检测性能,当采样率为0.5时,前者的AUC达到0.989,其检测性能与单位采样矩阵相近,而此时传统压缩采样矩阵的AUC值仅为0.914,这说明,利用稀疏模型先验知识改进压缩采样矩阵,能够降低压缩采样检测对采样率的要求,有效提升其检测性能。 当采样率K/L=0.4时,单位采样矩阵、传统随机压缩采样矩阵和经稀疏表示子空间改进后的压缩采样矩阵对应的ROC曲线如图8所示,其中误差棒曲线为100次重复实验检测概率的平均值和标准差。 图8 采样率为0.4时各种采样矩阵对应的ROC曲线Fig.8 ROC curves corresponding to different sampling matrix at sampling rate of 0.4 从图8可以看出,传统随机压缩采样矩阵的检测性能较差,而利用待测信号稀疏模型改进压缩采样矩阵后,其检测性能明显提升,在相同的虚警概率下,其检测概率总是高于传统随机压缩采样矩阵,且检测概率的标准差也明显减小,从0.002~0.174 降至0.001~0.081范围,说明利用稀疏模型先验知识改进压缩采样矩阵不仅能够提升压缩采样检测性能,还能够削弱采样矩阵的随机性对于检测性能的影响,增强压缩采样检测算法的鲁棒性。 本文将压缩信号处理理论引入光谱图像目标检测,研究了待测信号稀疏模型先验条件下,基于非重构压缩采样的光谱图像目标检测方法。首先讨论了传统压缩采样检测的边界性能;然后利用待测信号的稀疏表示子空间构造压缩采样矩阵,采用正交子空间投影法将压缩采样信号投影到干扰信号的局部正交子空间,抑制背景光谱的影响;最后对其检测性能进行了对比分析。实验和分析结果表明,该方法能够有效提升压缩采样检测算法的性能,削弱压缩采样矩阵随机性对于检测性能的影响,增强压缩采样检测算法的鲁棒性。
3 实验与分析
3.1 实验1

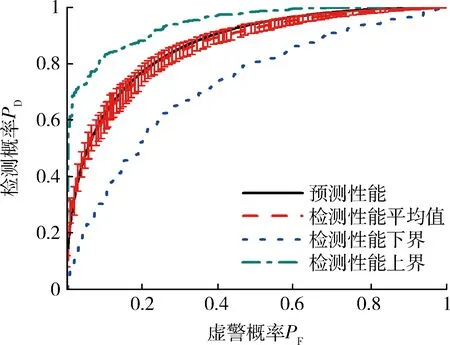
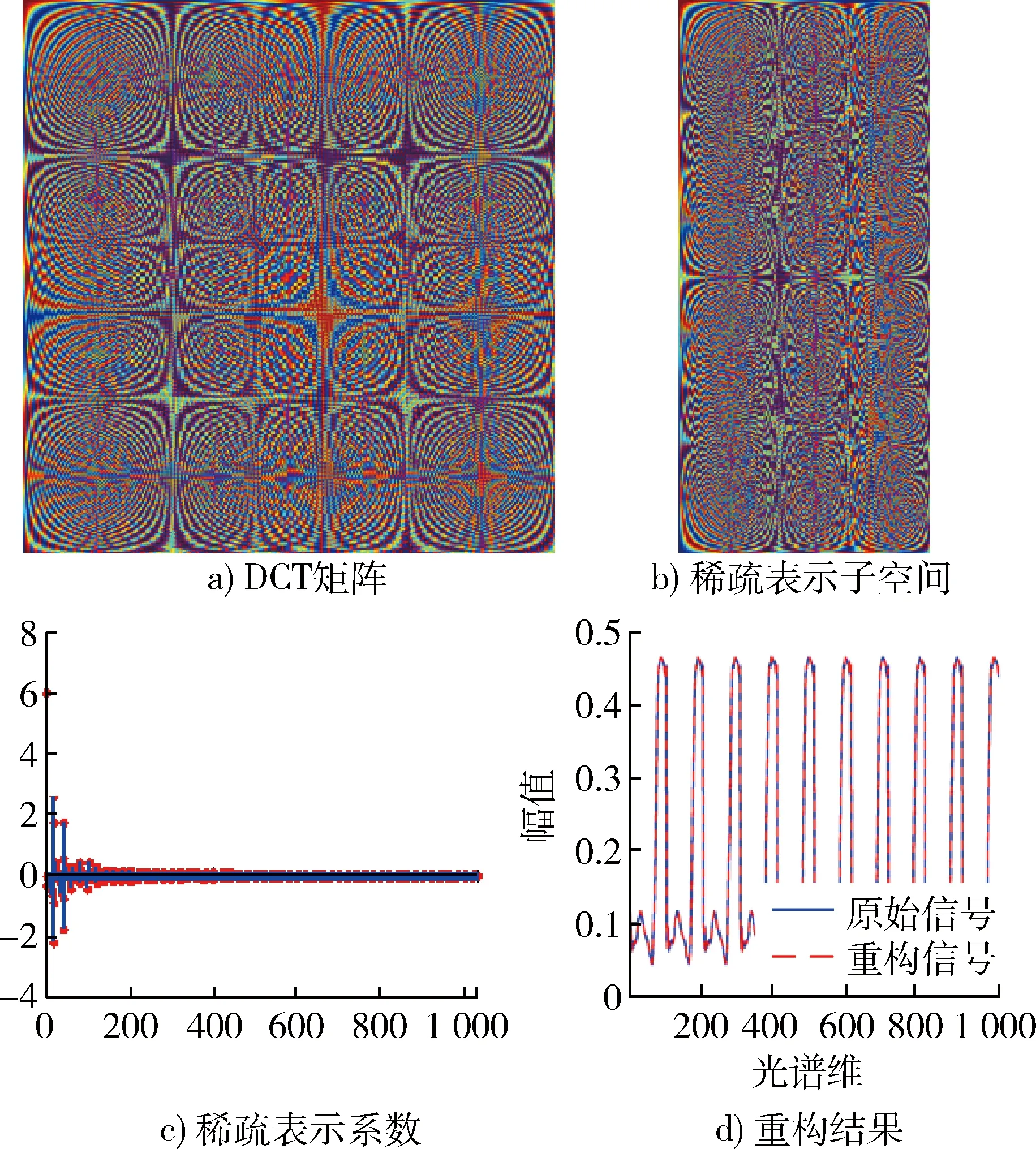

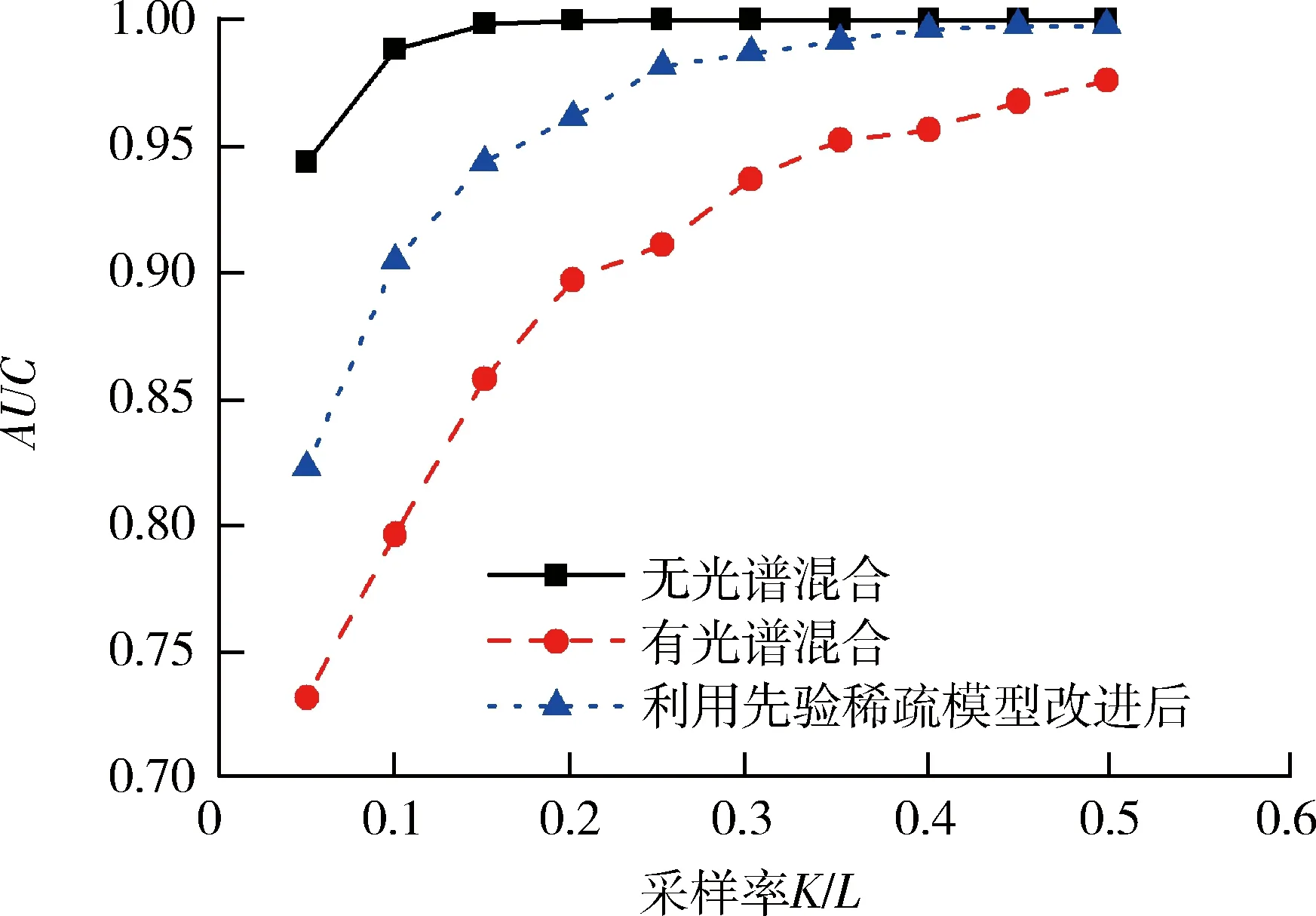
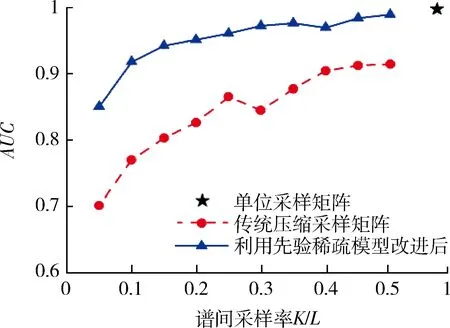
3.2 实验2


4 结束语
