基于二阶Keystone的微弱运动目标检测 *

翟心蝶，杨刚，廉杰

(北京遥感设备研究所，北京 100854)

0 引言

精确制导武器通过导引头中弹载雷达处理回波信号提取信息，实现对移动目标的识别、探测、跟踪。随着技术的发展，出现了具有体积小、距离远、会利用低反射面积隐身、信噪比或信杂比低、高速或高机动等特点的微弱运动目标，回波能量弱。弹载平台具有速度较快、机动性较高的特点，面对微弱运动目标传统的雷达目标检测方法难以检测跟踪[1-4]。为提高对这类目标的检测能力,如果采用大发射峰值功率与大功率孔径积的天线，存在受设备硬件限制、信号处理动态范围小、抗干扰能力差等问题,不适合弹载环境[5]。

现在通常会对信号进行积累以解决此类问题。根据是否需要相位信息，积累分为相参积累和非相参积累。为便于工程实现,弹载雷达多使用非相参积累，不要求系统的相参性。但非相参积累取模的非线性会导致积累增益损失，损失随原信噪比的降低而增大，低信噪比时不适用。相参积累是将回波信号在积累时间内进行相位补偿后相加，可同时获得雷达与目标间的相对径向速度，提高积累的增益。沿目标运动轨迹积累能量时，回波信号波形的瞬时幅度相对于时间变化的是确定的函数，能量可有效积累；噪声信号的相位随机，在相参积累时噪声能量积累效率低。因此对低信噪比目标的检测，可以通过延长相参积累时间达到提高雷达对微弱目标探测能力，提高多普勒频率分辨能力的效果。

由于目标的运动，在弹载雷达对微弱运动目标的处理过程中，导引头和目标间的会产生距离变化。长时间积累会产生跨越距离走动单元与跨速度单元现象，回波信号能量分散，传统的动目标检测(moving targets detection,MTD)方法积累效果差。因此，需要校正距离走动与多普勒走动[6-8]。

1 回波信号模型及分析

1.1 线性调频脉冲信号

雷达信号通常是线性调频(linear frequency modulation,LFM)脉冲信号，它是在载波上对频率进行线性调制。LFM通过对脉内频率的线性调制得到大的时宽带宽积，在保证较高的距离和速度分辨率的同时，保证雷达的探测距离，对能量和分辨率进行解耦合。

雷达基带信号为线性调频矩形信号，信号可表示为

(1)

式中：f0为中心频率;TP为矩形脉冲宽度;带宽为B，K=B/TP为调频斜率。

对回波信号数据作二维处理。设tr为快时间，ta为慢时间，ta=mTa，m=0,1,2,…，M-1，Ta为脉冲重复周期，每隔Ta就会发射一个脉冲。M为一次扫描期间发射的脉冲数，雷达接收时间t与快时间及慢时间之间的关系为t=tr+ta。则雷达发射的线性调频信号也可以构成的二维数据矩阵表示为

(2)

式中:fc为载波频率。

1.2 匀加速直线运动的目标回波模型

(3)

式中：

(4)

(5)

快时间域变换到基带频率域

(6)

对接收的回波信号做脉冲压缩处理，通过匹配滤波聚集脉内能量。匹配滤波是线性时不变的，回波通过匹配滤波器的输出可以用输入信号与匹配滤波器冲激响应的卷积。

(7)

Xr(f,ta)=Sr(f,ta)H(f)=

(8)

对(8)式作IFFT，脉冲压缩后信号时域形式为

exp[jπfd(tr+2ta+τm)]·

(9)

1．3 距离走动

在进行相参积累时，目标回波应位于同一单元内，才能进行后续的脉冲压缩。若跨越到其他单元，但又基于同一个距离单元作积累，则会影响雷达的检测性能。由于防空导弹的运行速度快，弹目间产生距离的变化也快。

(10)

式中：ΔR为距离单元大小；floor为向下取整[9]。

因此，对高速目标作长时间积累时会有距离走动，应校正Nm个距离单元的走动，使相干积累时间得到延长，从而提高雷达系统对低可探测目标的检测性能。

如图1，雷达发射的脉冲数为128个，目标速度为1 000 m/s，调频信号带宽为10 MHz,脉冲宽度10 μs，脉冲重复频率1 000 Hz，跨越了25个距离单元。图1为直接进行脉冲压缩未校正经距离走动的结果，可以看出，第1个脉冲与第128个脉冲之间存在距离走动。

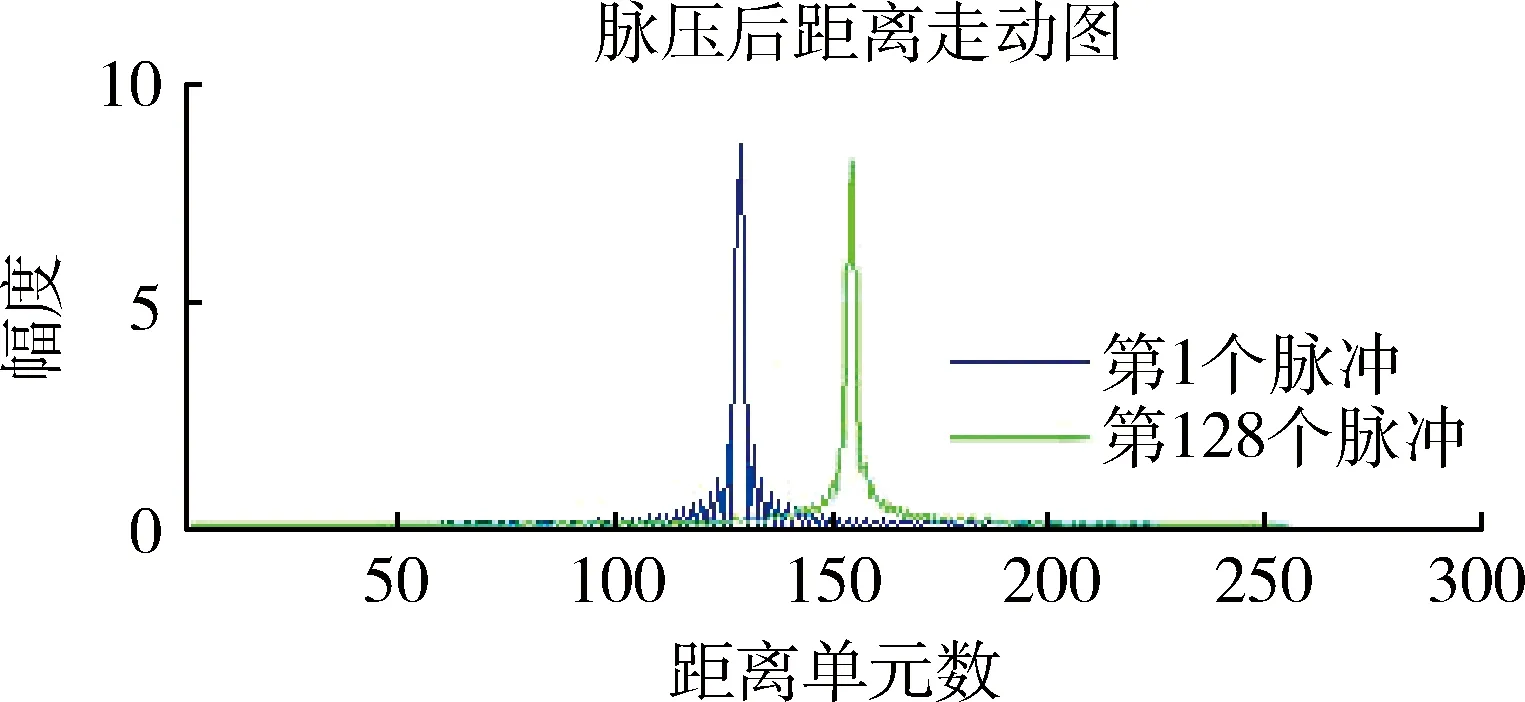
图1 不同脉冲脉压结果图Fig.1 Pulse compression results of different pulses

所以对目标信号回波直接做相干积累时，各个脉冲回波包络峰值的走动会降低脉冲能量的积累增益。

2 基于Keystone变换的距离走动校正

2.1 一阶Keystone变换

2.1.1 Keystone校正距离走动原理

Keystone变换是对回波的距离单元走动校正的一种方法。其优点在于，在校正目标的线性距离走动时不需要目标运动参数先验信息，并在校正走动的同时保持回波信号的相位关系，适用于通过相参积累提高检测信噪比[10]。

Keystone (楔石形)是对线性变换方法的一种形象描述，通过变量代换使二维平面上的矩形在距离-频率平面上变成一个倒梯形。雷达成像中的Keystone变换是对慢时间轴的伸缩变换，频率越高伸缩幅度越大。雷达回波的支撑域是一个二维平面，是一个由脉内快时间和脉间慢时间(即距离和脉冲数)构成的二维数据矩阵，通过在距离向时间域进行FFT,把这个二维平面映射到距离-频率方位时间平面上[11-12]。

设虚拟时间τa，并令τa=mT′,其中T′虚拟慢时间对应的脉冲重复间隔。Keystone的变换尺度为

Keystone变换有sinc内插法、DFT-IFFT，Chirp-Z变换等实现算法。

(1) sinc插值

sinc内插法，通过在距离频率-方位时间域对慢时间进行插值重构，尺度变换后的坐标没有对应的采样值，因此变换时需要通过插值运算进行估值重建初始信号：

(11)

式中：m为原τa的采样点，n为内插后的采样点n=0,1，…,M-1为内插之后以′T为间隔的采样点。

(2) DFT-IFFT

(12)

此时的DFT是变尺度的DFT，不能直接由FFT实现。然后做逆傅里叶变换，可得到

(13)

(3) CZT-IFFT

设一有限长序列x(n)(0≤n≤N-1)，其Chirp-Z变换可表示为

(14)

式中：A=A0ejθ0，W=W0e-jφ0，表示起始抽样点z0=A0ejθ0的矢量半径长度；W0为螺线的伸展率；θ0为起始抽样点的相位角；φ0为相邻两抽样点间的角度差[13]。

2.1.2 Keystone实现方法运算量比较

设相参积累的脉冲数为M，每个脉冲的采样点个数为N，M和N都为2的整数次幂。

(1) sinc插值

M组N个点进行sinc内插运算，有M·N·M次复乘。

(2) DFT-IFFT

(3) CZT-IFFT

2．2 二阶Keystone变换

2.2.1 二阶Keystone校正距离走动

一阶Keystone变换仅能校正弹目间匀速运动引起的距离走动，对于弹目间径向加速度引起的距离弯曲则不能校正掉。弹载雷达仅依靠平台速度进行距离弯曲的补偿，难以把距离弯曲补偿误差控制在一个距离分辨单元内。因此在目标的运动参数未知的情况下，可以利用二阶Keystone变换的方法消除距离弯曲。

尺度变换公式定义为

对信号进行一次二阶Keystone变换后得到：

(15)

但由速度引起的线性距离走动仍然没有得到完全校正，也就是说距离走动依旧存在，只是动量为原来的一半，距离向频率和方位向时间的耦合没有解除，所以再做一次二阶变换。

对信号进行第二次二阶Keystone变换后得到：

exp(j2πfdτa).

(16)

由式(16)可以看出，经过二阶Keystone变换与二阶相位进行补偿后的目标回波，与目标径向速度有关的多普勒项及与目标径向加速度有关的多普勒调频率项均被补偿，信号包络峰值与脉冲数无关，实现了距离走动与距离弯曲校正[15-17]。

2.2.2 二阶Keystone变换的实现

同理于一阶Keystone时Chirp-Z变换，用CZT变换方式实现二阶Keystone变换的流程如下[18]：

(1) 设L为满足L≥N+M-1且为2的整数幂的最小正整数。其中M为一个CPI内的脉冲数。

(17)

用FFT求序列的DFT得

(18)

(3) 作L点的序列h(n)

(19)

(20)

(4) 作圆周卷积

V(r)=G(r)H(r)，

(21)

v(r)=IFFT(V(r)).

(22)

(5) 取前M点加权得到

(23)

对x(ZK)进行慢时间维IFFT，完成1次变换。第1次二阶Keystone变换后速度影响的多普勒项变为

(24)

耦合还存在，需第2次二阶Keystone变换之后再对快时间作IFFT，完成脉冲压缩：

y(f,τa)=IFFTr{IFFTa[x(ZK)]}

(25)

最后再对慢时间作FFT，最终实现对微弱目标的长时间相参积累和检测。

用二阶Keystone方法实现距离弯曲和距离走动校正的流程如图2所示。

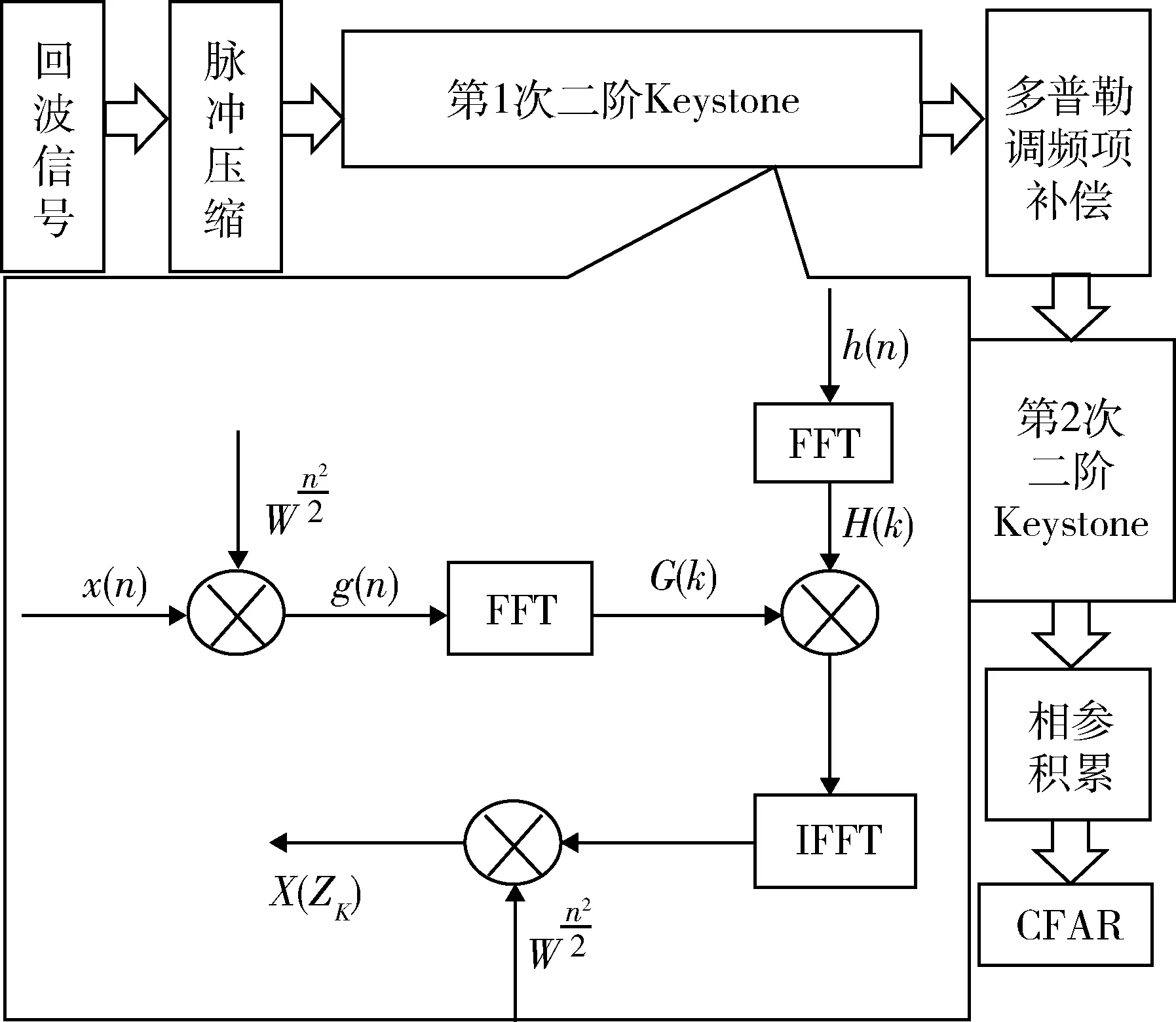
图2 微弱目标算法流程图Fig.2 Algorithm flow chart of weak moving target

3 仿真结果

3.1 距离走动校正效果仿真

为验证算法对微弱目标检测的有效性，设置仿真参数如下表1所示。

表1 仿真参数表Table 1 Simulation parameters

图3为用二阶Keystone方法校正距离走动前后不同脉冲的脉冲压缩图。可以看到，经过校正不同脉冲被校正到同一个距离单元，便于相参积累。

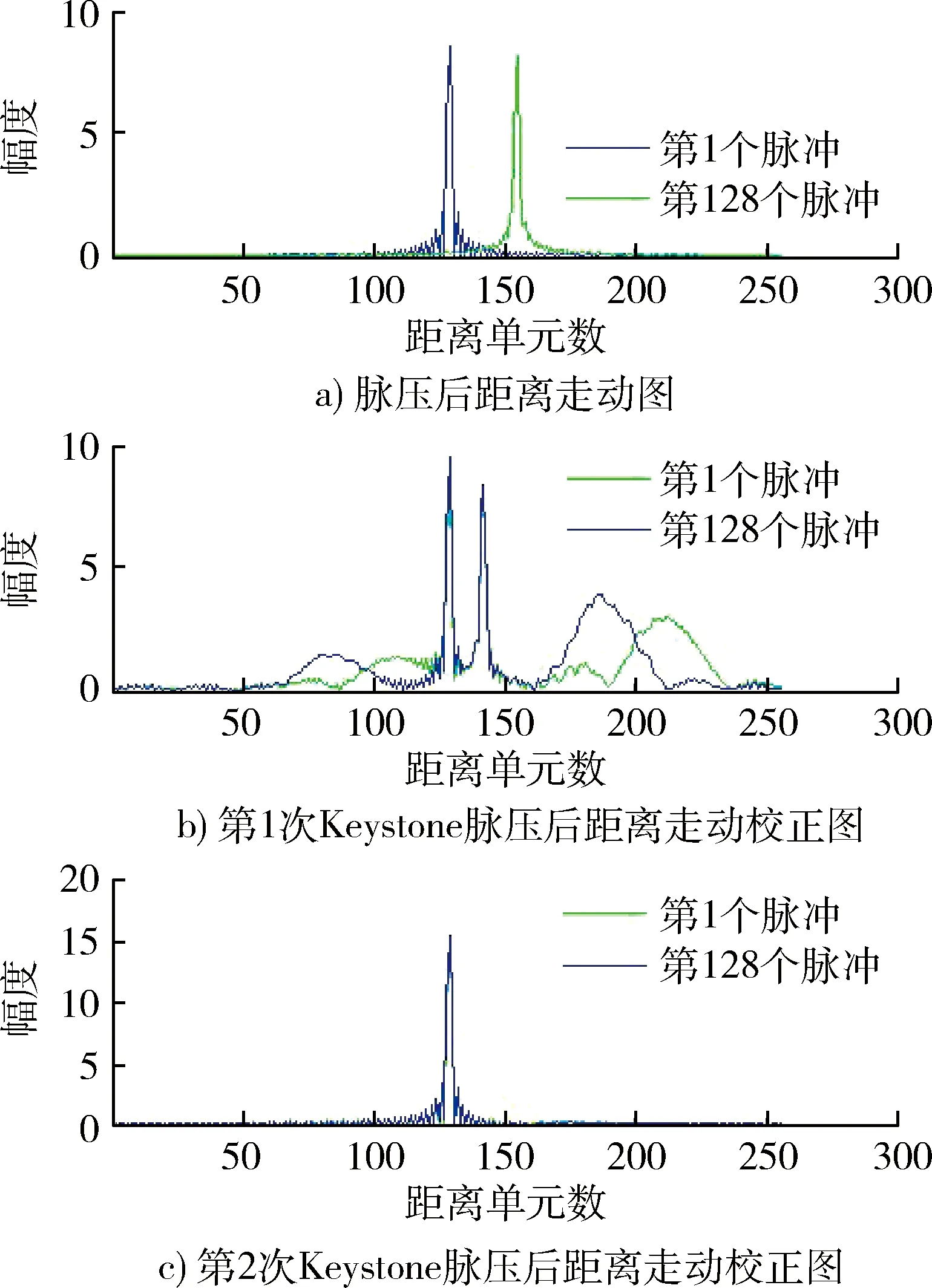
图3 校正前后脉压结果图Fig.3 Pulse compression result of before and after correction

用仿真验证二阶Keystone方法对目标回波的距离弯曲与走动校正的效果。图4-7为没有加入高斯白噪时，校正前、经过距离弯曲校正、距离走动校正后的结果。

如图4，5，当脉冲积累数少也就是积累时间较短时，可以看到尽管目标存在加速度，但距离弯曲不明显。延长积累时间后可以看出，距离弯曲会影响到信号包络的对齐，仅经过2次二阶Keystone校正后，存在多普勒走动的影响。当加速度为 150 m/s2时，经过二阶相位补偿后可得到的结果如图6。此时由于加速度引起的距离弯曲不明显，将加速度提高到500 m/s2，积累的脉冲数提高到512个，可以直观地观察到多普勒调频项影响的距离弯曲与校正的效果。如图7可以看到，在第1次二阶Keystone校正后，包络走动的距离弯曲能被有效的改善，且距离走动动量为原来的一半，在二阶相位补偿后，弯曲完全被消除，但距离走动仍然存在。经过了2次二阶Keystone校正与相位补偿后，信号包络成功校正到了同一距离单元。

图4 (128个脉冲)未相位补偿效果图Fig.4 Effect without phase compensation (128 pulse)

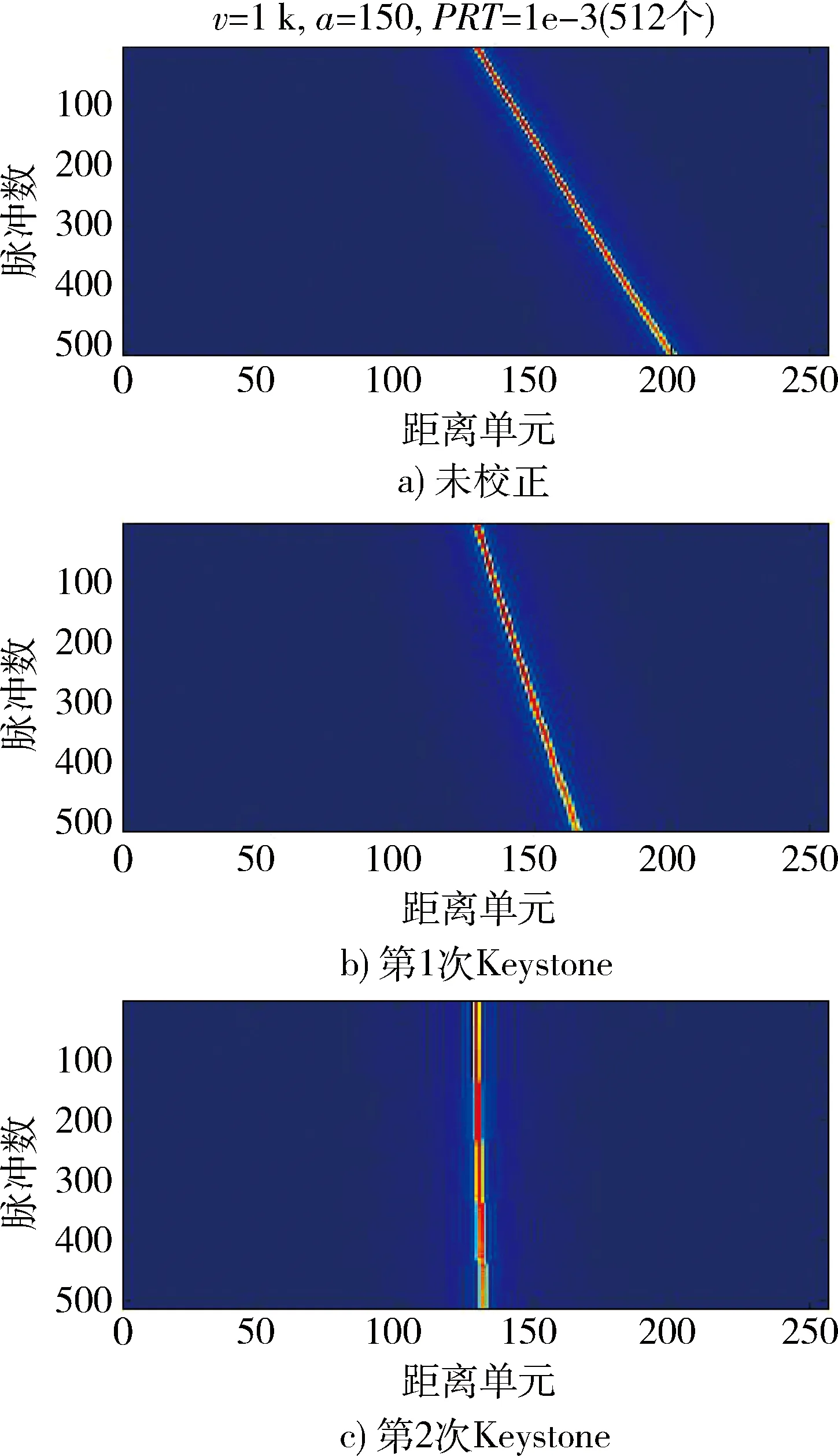
图5 (512个脉冲)未相位补偿效果图Fig.5 Effect without phase compensation (512 pulse)

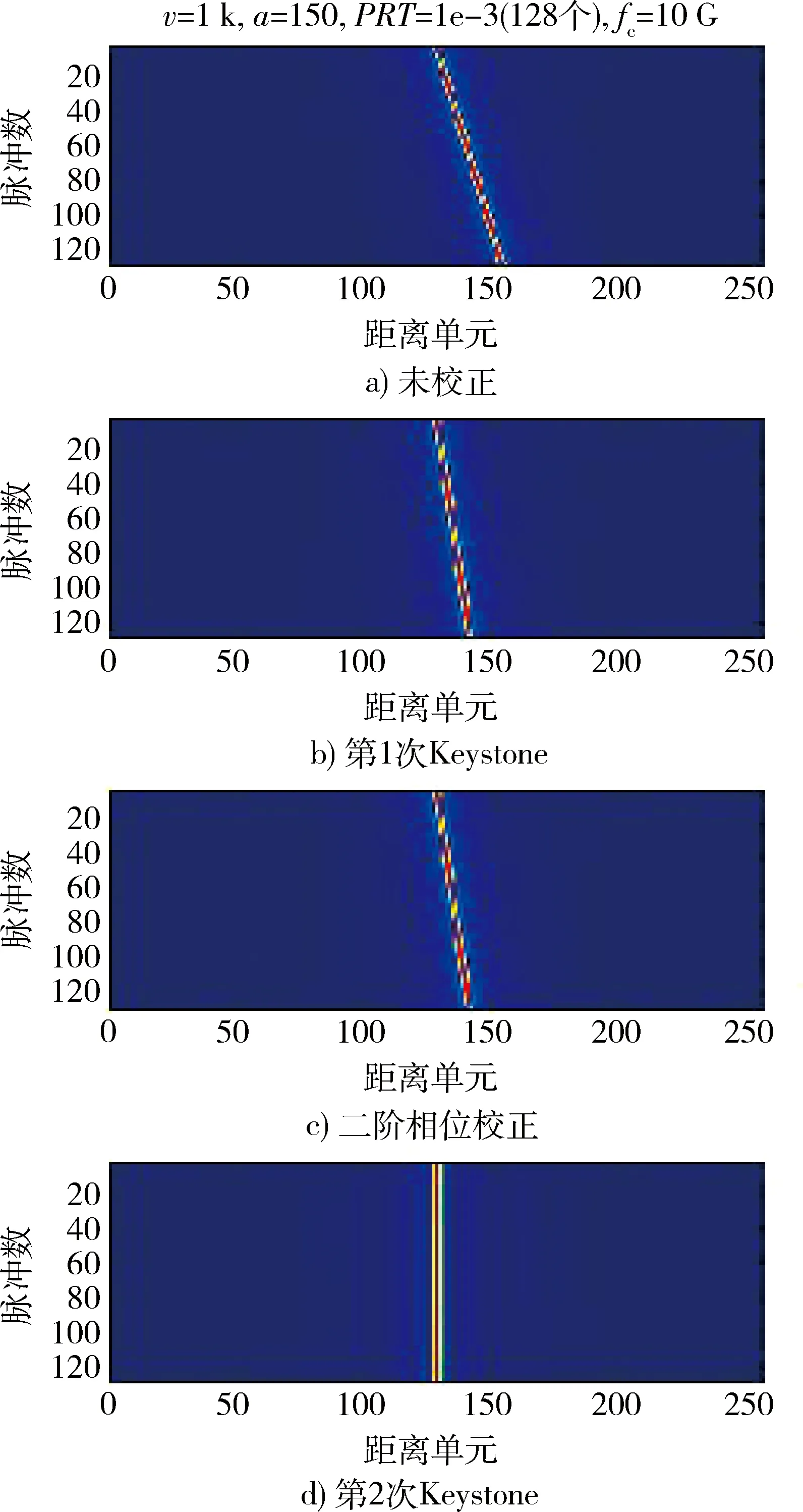
图6 (128个脉冲)二阶Keystone校正效果图Fig.6 Effect of second-order Keystone transform (128 pulse)

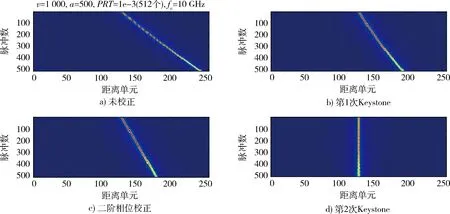
图7 (512个脉冲)二阶Keystone校正效果图Fig.7 Effect of second-order Keystone transform (512 pulse)

3.2 不同方法检测性能对比

如果给信号加入高斯白噪。由于信号波形是随时间规律的变化，而噪声随时间变化是不确定的，可以利用延长积累的方法来提高信噪比。

理想的积累器积累个Np信号，相参积累使信噪比改善为原来的Np倍，即增益为10lgNp。脉冲压缩的信噪比增益为10lgD，其中D是脉冲压缩比，D=BTP。则积累后SNRout=SNRin+10lgNp+10lgD[16]。

下图为信噪比为SNR=12 dB时，不同校正方法下的仿真结果。

图8中，8a)为对脉压后的回波信号用MTD的方法直接做相参积累，目标回波信号完全淹没在噪声中；8b)为在雷达测距后利用差分的方法估计目标的速度与加速度，估计的精度存在一定的误差，对积累后的结果有影响，回波能量分散，不能够对目标进行有效检测；8c)为用一阶Keystone的方法校正，没有对由径向加速度运动而产生的距离弯曲进行校正，没有解决多普勒频谱扩展问题；8d)二阶Keystone变换后，信号未有极大扩散，可以对目标进行有效的检测。

图8 SNR=-12 dB时仿真结果图Fig.8 Simulation results with SNR=-12 dB

用二阶Keystone的方法校正，信噪比相较于MTD方法提高17 dB。同一距离单元内可对128个脉冲做有效相参积累时，可得到积累增益约21 dB，利于检测微弱目标。

4 结束语

本文研究了微弱运动目标匀加速运动时的回波信号模型，分析其中引起距离走动的多普勒项与引起距离弯曲的多普勒频率调频项。分析对比用Keyston变换校正距离走动的实现方法的计算量。且由于径向距离变化率是时间的高次幂函数，引入二阶Keystone算法校正距离走动与距离弯曲[19]。选择了用CZT-IFFT二阶Keystone的方法进行校正，结合对加速度引起的二阶相位进行补偿，达到了将包络轨迹对齐，使能量聚集的目的。并加入高斯白噪声，将MTD方法、差分方法估计速度、一阶Keystone、二阶Keystone方法的校正效果作比较，对比了不同校正方法的信噪比改善效果。