基于模糊-ADC的反舰导弹武器系统效能评估方法研究 *

杨剑波，宗思光

(海军工程大学 电子工程学院，湖北 武汉 430033)

0 引言

随着信息时代高科技的快速发展，在制空权、制海权的激烈争夺背景下，超视距远程精确打击成为现代海战的必然要求，以反舰导弹为典型的精确制导武器的运用是争夺制海权的有效途径，也是现代海战的一种主要模式[1]。随着各国水面舰艇配备的反导装备战技性能指标的提升和反导防御手段方式的多样化，反舰导弹的突防能力面临着严峻的制约与挑战。在这大背景之下，如何有效地对反舰导弹武器系统在对抗条件下进行合理的效能评估问题就显得尤为重要。

以往相关文献大多集中阐述反舰导弹的捕捉能力、命中能力、毁伤能力、突防能力等相关内容[2-9]，对反舰导弹武器系统整体的效能评估相对较少。文献[10]提出了基于贝叶斯网络的常规导弹反舰作战效能评估方法，受外部环境影响较大；文献[11]结合贝叶斯网络和熵权法，构建了反舰导弹全作战流程的效能评估模型，但欠缺对时间性指标的考虑；文献[12]提出基于网络层次分析法和熵权法组合的反舰导弹作战体系效能评估方法，但受制于评估指标体系不够健全、评估数据不够准确。

反舰导弹武器系统涉及火控、侦察、跟踪、打击等多个层次、多个维度的关联与耦合，其作战效能难以用某一种特定的评估模型来进行量化性质的评估，且构建的模型中既会涉及具体指标计算，也会有专家打分评价的主观判断，传统纯计算的数学方法是难以适应这类决策问题，就需要引进模糊数学的理论和方法。在众多评估法中，ADC(Analog-to-Digital Converter)模型[13-14]侧重于从系统的角度考量其可用性、可靠性和能力等综合效能；AHP(Analytic Hierarchy Process)层次分析法[15]能够确定指标权重；模糊综合评判法偏向于描述边界不清楚、难以定量分析的问题，这三者的结合可以较好地评价武器系统的整体综合性能，能将专家的主观评估与仿真结果相结合，使得评估结果更加贴近军事作战实际。

1 ADC模型简介

ADC模型是指美国工业界武器系统效能咨询委员会提出的评价武器系统常用的模型和方法，该方法用数学表达式可表示为

E=ADC,

(1)

式中:表明系统的效能(E)是由其可用性(A)、可信性(D)和能力(C)三大部分组成，它结合可用性、可信性和能力3方面较为全面地反映武器系统的综合效能，并通过E=ADC的计算，把性能参数最终量化为具体的分值，更加直观地对武器系统的进行评分，较为客观地评价武器系统的综合效能，并方便了各类武器效能评估的对比。

2 反舰导弹武器系统作战效能评价指标体系

2.1 确定系统可用性模型A

反舰导弹武器系统的可用性模型，主要考虑其系统组成，由于其独特的作战用途，其绝大部分功能都集成在反舰导弹上，反舰导弹主要是由弹头段、导引段和推进段组成，导弹可以通过以上的功能达到“全自动、射后不理”的程度。我们可以把可用性模型简化成2部分，发射平台和导弹单元，每个部分均由2种情况(正常和故障)组成，所以把系统分为4种状态[16]。

状态1：导弹单元正常，发射平台正常；

状态2：导弹单元正常，发射平台故障；

状态3：导弹单元故障，发射平台正常；

状态4：导弹单元故障，发射平台故障。

根据以上4种状态，把反舰导弹武器系统可用性A表示为

A=(a1,a2,a3,a4),

(2)

式中：a1,a2,a3,a4分别表示系统4种状态的概率，可以得到：

A=(aMaH,aM(1-aH),(1-aM)aH,

(1-aM)(1-aH)),

(3)

式中：aM,aH分别表示导弹单元正常工作的概率和发射平台正常工作的概率。概率的计算公式为

(4)

式中：MTBF为系统平均无故障工作时间;MTTR为系统平均故障修复时间。

2.2 确定系统可信性模型D

可信性表示的是系统在工作期间的各部位状态的变化，即正常运作概率的变化。按照上述设定的4种可能状态，可信性矩阵D是一个4×4的矩阵。

(5)

式中：dij表示系统开始处于i状态，在作战过程中转移到j状态的概率。在作战使用过程中出现的故障问题，由于时间紧张，我们视作为无法维修修复，则就不能使故障状态转换为正常状态，所以可信性矩阵D就成为了上三角矩阵[17]。

(6)

设Mij为导弹单元从状态i到状态j的概率，Hij为发射平台从状态i到状态j的概率。PM为导弹单元故障概率，PH为发射平台故障概率。

M11=1-PM,M12=PM,M21=0,M22=1,H11=1-PH,H12=PH,H21=0,H22=1.

(7)

由于反舰导弹武器系统的分系统是串联形式构成，所以：

d11=M11H11,d12=M11H12,d13=M12H11,

d14=M12H12;

d21=M11H21,d22=M11H22,d23=M12H21,

d24=M12H22;

d31=M21H11,d32=M21H12,d33=M22H11,

d34=M22H12;

d41=M21H21,d42=M21H22,d43=M22H21,

d44=M22H22.

(8)

2.3 确定系统能力模型C

根据反舰导弹武器系统的特点及发展趋势，结合反舰导弹成功完成打击任务的过程，总结提炼了影响反舰导弹作战效能能力指标的4个方面，分别为导弹捕捉能力、命中能力、毁伤能力和突防能力。对这四方面影响因素进行细化分析，进一步提出影响子指标的二级指标和三级指标[2-9]。整体的反舰导弹武器系统能力评估指标体系见图1。

采用层次分析法和模糊综合评判法量化处理能力矩阵C，具体步骤：

(1) 利用层次分析法，计算反舰导弹武器系统能力评估指标体系A中准则层B1～B4、子准则层C11～C44和方案层C111～C433各指标的相对权重，并对计算结果进行一致性检验，最终得到反舰导弹武器系统能力评估指标体系权重表。

(2) 根据图1，反舰导弹武器系统能力评估因素域为

U={u1,u2,u3,u4},

(9)

式中：

u1={u11,u12,u13,u14}；u2={u21,u22,u23,u24}；
u3={u31,u32}；u4={u41,u42,u43,u44}.

(10)

(3) 确定评语等级集合V

V={v1,v2,v3,v4,v5}=

{优秀，中上，中等，中下，差}=

{1,0.85,0.75,0.7,0.6}.

(11)

(4) 构建模糊关系矩阵R

(12)

式中：rij为各层评估因素域U中元素ui所对应评语等级集合V中的等级vj的隶属关系，即R也成为隶属度矩阵。

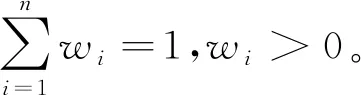
(6) 计算模糊综合评判矩阵。对比4种合成算子，可得算子M(•,⊕)能充分利用矩阵R的信息，且综合程度强，并且属于加权平均型，较为地明显体现出权数作用，所以最终选择算子M(•,⊕)来进行模糊算法的复合运算[18]。表达式为

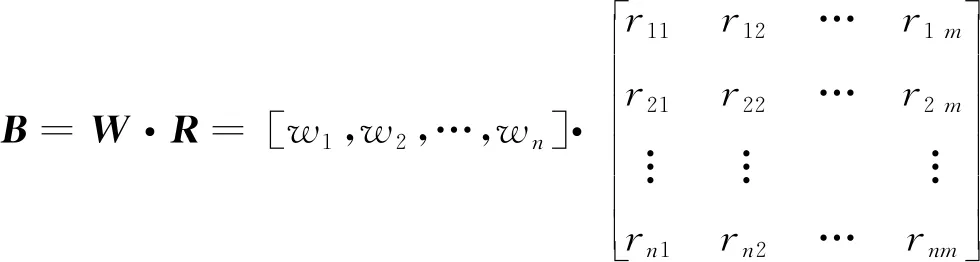
(13)

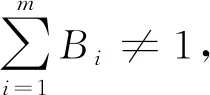
(7) 计算能力值c1。利用c1=B·VT，计算能力值c1的评分。

3 仿真校验

假设某型反舰导弹对某海域一水面舰艇进行攻击，该水面舰艇配备有舰载防空导弹、舰炮和有源无源干扰设备。

3.1 计算可用性矩阵A

该反舰导弹导弹单元和发射平台的MTBF，MTTR见表1。

表1 各平台的MTBF和MTTRTable 1 MTBF and MTTR of each platform

根据表1和式(3)，(4)，可得：

aM=0.988,aH=0.984,A=(aMaH,aM(1-aH),(1-aM)aH,(1-aM)(1-aH))=
(0.972,0.016,0.012,0).

3.2 计算可信性矩阵D

假设导弹单元发动机故障概率为PM=0.02,发射平台的故障概率为PH=0.04，根据式(6)～(8)可得：

3.3 计算能力矩阵C

3.3.1 确定指标权重

根据专家打分，通过层次分析法(AHP)构造判断矩阵(见表2)，并进行一致性检验。

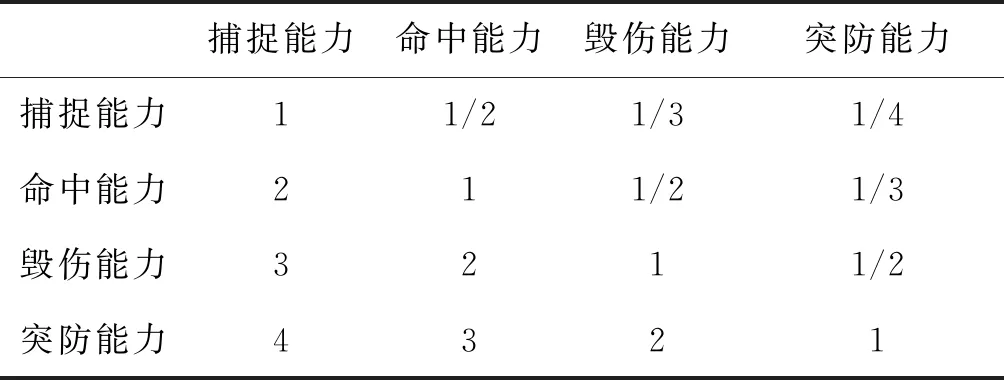
表2 能力准则层判断矩阵Table 2 Competency criterion level judgment matrix

计算得：ω=(0.095 4,0.160 1,0.277 2,0.467 3)，λmax=4.031,C.I=(λmax-n)/(n-1)=(4.031-4)/3=0.010 3查表得，当n=4时，修正系数R.I=0.89，则C.R=C.I/R.I=0.010 3/0.89=0.011 6<0.1，从此可以判断矩阵具有一致性。根据此方法计算出反舰导弹武器系统能力评估指标体系权重表，如图2所示，为确保结果的公平公正性，邀请10名专家,让他们分别对各指标进行优劣评判，进行打分。

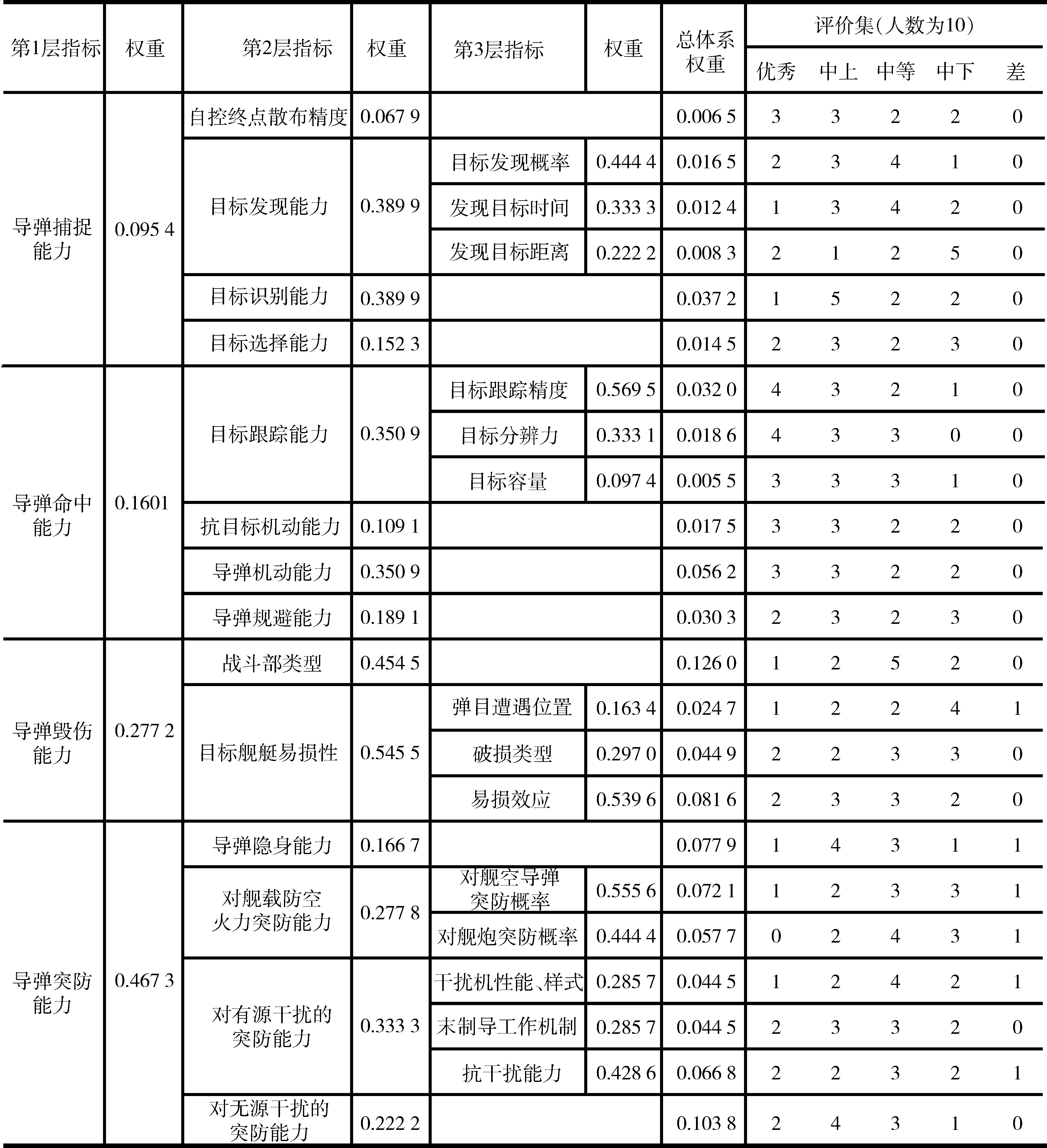
图2 反舰导弹武器系统能力评估指标体系权重图Fig.2 Weight table of anti-ship missile weapon system capability evaluation index system

3.3.2 指标体系3级模糊综合评判

令rimn=(fimn1,fimn2,fimn3,fimn4,fimn5)，其中fimne表示3级指标层第imn个指标因子Cimn相对于评价集V={v1,v2,…,ve}中评语的隶属度。

(14)

根据式(14)和图2中的专家打分情况，计算得到3级指标层各因素隶属行向量为

r121=(0.2,0.3,0.4,0.1,0)
r122=(0.1,0.3,0.4,0.2,0)
r123=(0.2,0.1,0.2,0.5,0)
r211=(0.4,0.3,0.2,0.1,0)
r212=(0.4,0.3,0.3,0,0)
r213=(0.3,0.3,0.3,0.1,0)
r321=(0.1,0.2,0.2,0.4,0.1)
r322=(0.2,0.2,0.3,0.3,0)
r323=(0.2,0.3,0.3,0.2,0)
r421=(0.1,0.2,0.3,0.3,0.1)
r422=(0,0.2,0.4,0.3,0.1)
r431=(0.1,0.2,0.4,0.2,0.1)
r432=(0.2,0.3,0.3,0.2,0)
r433=(0.2,0.2,0.3,0.2,0.1)

利用以上数据，根据式(9)～(13)进行模糊关系合成运算，令

将结果归一化，得

k′12=(0.166 7,0.255 6,0.355 6,0.222 2,0),

同理可得:

k21=(0.390 3,0.300 0,0.243 0, 0.066 7,0)=k′21.
k32=(0.183 7,0.254 0,0.283 7, 0.262 3,0.016 3)=k′32.
k42=(0.055 6,0.200 0,0.344 4, 0.300 0,0.100 0)=k′42.
k43=(0.171 4,0.228 6,0.328 6, 0.200 0,0.071 4)=k′43.

3.3.3 指标体系2级模糊综合评判

确定2级模糊关系隶属度矩阵

K={K1,K2,K3,K4},

式中：

同理可得：

S2=(0.312 8,0.3,0.215 1,0.172 1,0)=S′2，
S3=(0.145 6,0.229 5,0.382 0, 0.234 0,0.008 9)=S′3，
S4=(0.133 7,0.287 3,0.321 9, 0.188 9,0.068 2)=S′4.

3.3.4 指标体系1级模糊综合评判

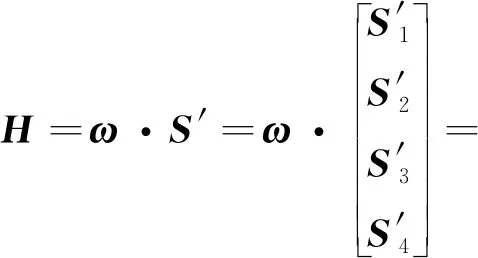
3.3.5 计算能力得分

根据4种状态，最终确定

C=(c1,0,0,0)T=(0.804 7,0,0,0)T.

3.4 计算综合效能E

该型反舰导弹综合得分为0.736 0，对照评分等级来说，属于中等偏上水平。但对比能力矩阵计算出来的得分水平，下滑明显，说明在反舰导弹武器系统发射过程前和过程中，均存在一定的故障概率。结合系统整体的可用性和可信性来看，考虑了整体故障的角度，综合得分下滑明显，也属于正常状态，并未出现大等级的下滑，均在中等偏上徘徊，符合武器系统使用规律。

3.5 打击不同水面舰艇综合得分情况

以上的得分只是针对某类水面舰艇，对于其他类型的水面舰艇，并没有直观的体现。为了横向对比，假设对于不同的水面舰艇都有相同的防空反导能力。在反舰导弹武器系统能力评估指标中，直接影响的指标有抗目标机动能力与目标舰艇易损性2个2级指标，针对下属的3级指标，重新进行优劣评判，判断对该型反舰导弹的影响,如表3，4所示。

表3 水面舰艇2相关指标评判Table 3 Evaluation of relevant indexes of surface ship 2

3种类型水面舰艇的综合评分分别为0.736 0,0.736 4和0.737 8，相差无几。从图2中的总体系权重可以看出，4项指标总体系权重之和为0.168 7，针对本文中提到的典型水面舰艇，通过计算结果分析得出不同类型水面舰艇(外部因素)并不是影响该型反舰导弹武器系统效能的主要指标。

根据以上数据，计算得c1=0.805 1，E=0.736 4。

表4 水面舰艇3相关指标评判Table 4 Evaluation of relevant indexes of surface ship 3

根据以上数据，计算得c1=0.806 7，E=0.737 8。

通过图2的总体系权重栏，查找剩余指标。发现总体系权重值较大(>0.1)有战斗部类型和对无源干扰的突防能力2项，均为其本身属性。按照这2项情况极端变化进行量化计算(针对水面舰艇1),可得：

(1) 战斗部类型：全优秀，c1=0.831 8，E=0.760 8；全差，c1=0.781 4，E=0.714 7。

(2) 对无源干扰的突防能力：全优秀，c1=0.821 8，E=0.751 7；全差，c1=0.780 3，E=0.713 7。

这2项中的某一项的急剧变化容易导致得分的骤变，两者的全优秀均在0.75以上，为中等水平，稍有变化，就会跌落到接近中等偏下水平，从以上数据来看，这两者对反舰导弹武器效能敏感性最强。在军事斗争中，只有顺利突防，才能有效毁伤。

4 结束语

在高科技时代背景下反舰导弹的技术水平逐步提升，在科技人员的努力下故障率等一系列影响武器系统的参数正逐步改进，对武器系统本身的影响正在降低。对于各型反舰导弹而言，可用性A和可信性D相差不大，差异主要体现在能力矩阵C上，所以在本文中，重点介绍并计算了能力矩阵C。

本文以某型反舰导弹武器系统为研究对象，对其特征属性进行分析，构建了以ADC模型、层次分析法(AHP)和模糊综合评判法为基础的一种效能评估方法，该方法将定性分析与定量计算相结合，最终用分数的形式直观体现了武器系统效能，方便了各型反舰导弹进行综合效能的比较。本文也通过分析不同因素对反舰导弹武器系统整体效能的影响，为未来反舰导弹的研发和使用提供借鉴和参考。