山区高速公路桥梁圆柱式墩抗震设计

李海洋

摘 要：山区高速公路的突出特点是地形条件复杂、桥隧比高、施工条件差。根据墩高不同，桥墩一般采用圆柱式墩、方墩、箱型墩等设计方案。方墩、箱型墩需要设置群桩基础，基础尺寸较大，其需要开挖较大的施工平台，对山体的破坏比较严重。为贯彻“绿色公路”设计理念，桥墩应尽可能避免设置群桩基础，采用圆柱式墩。本文利用Midas有限元软件，建立了35 m墩高圆柱式桥墩有限元分析模型，验算在Ⅶ度区地震作用下桥墩的抗震性能。结果表明，圆柱式墩满足抗震要求，这就为山区高速公路项目圆柱式墩设计提供了参考。

关键词：山区高速公路;圆柱式墩;抗震

中图分类号：U442.55 文献标识码：A 文章编号：1003-5168（2021）06-0104-03

Seismic Design of Cylindrical Piers of Mountain Expressway Bridges

LI Haiyang

（Henan Provincial Communications Planning & Design Institute Co.， Ltd.，Zhengzhou Henan 450000）

Abstract： The outstanding features of mountain expressways are complex terrain conditions， high bridge-tunnel ratios， and poor construction conditions. According to different pier heights， the piers generally adopt cylindrical piers， square piers， box piers and other design schemes. Square piers and box-shaped piers need to be equipped with group pile foundations， and the foundation size is larger， which requires a larger construction platform to be excavated， and the damage to the mountain is more serious. In order to implement the "green highway" design concept， the piers should avoid setting pile foundations as much as possible and adopt cylindrical piers. In this paper， by using Midas finite element software， a finite element analysis model of a 35 m pier height cylindrical pier was established， and the seismic performance of the pier under the action of an earthquake in the Ⅶ degree area was checked. The results show that the cylindrical pier meets the seismic requirements， which provides a reference for the design of the cylindrical pier in mountainous expressway projects.

Keywords： mountain expressway;cylindrical pier;earthquake resistance

隨着社会经济的快速发展，我国高速公路建设实现了跨越式增长。高速公路的建设区域已由平原区、丘陵低山区逐步向山岭重丘区延伸。山区高速公路的特点是地形条件复杂、桥隧比高且施工条件较差。一般情况下，山区高速公路桥墩设计原则为：当墩高[h]≤25 m时，桥墩结构采用圆柱式墩+桩基础方案;当25 m<[h]≤35 m时，采用方墩+群桩基础方案;当35 m<[h]≤60 m时，采用空心墩+群桩基础方案。

圆柱式墩+桩基础方案具有外形美观、圬工体积少、施工工艺成熟与便利等特点，但其强度与稳定性较方墩与箱型墩差。方墩或箱型墩+群桩基础方案具有强度、稳定性高的特点，但该方案施工工艺复杂，而且群桩基础尺寸一般较大，施工过程中需要开挖较大的作业平台，对高速公路项目沿线自然景观破坏较大，与近年来所贯彻的“绿色公路”设计理念不符。因此，山区高速公路桥梁设计应尽量减少群桩基础的设置，多采用圆柱式桥墩设计方案。本文利用Midas有限元分析软件，建立了35 m墩高圆柱式墩有限元分析模型，验算在Ⅶ度区地震动峰值加速度0.10[g]（1 g=9.8 m/s2）情况下的抗震性能。结果表明，桥墩在E1地震作用下的强度条件满足设计要求;在E2地震作用下，桥墩出现塑性铰，顺桥向、横桥向塑性铰区抗剪强度以及位移均能满足抗震要求[1]。

1 计算模型

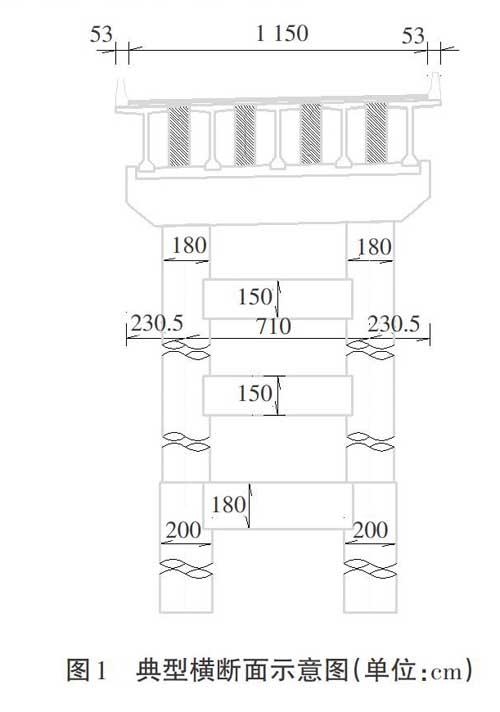
根据山区高速公路特点，30 m和40 m跨径预应力混凝土装配式T梁是山区高速公路中小跨径桥梁上部结构的首选。本研究选取典型设计，即时速100 km/h、路基断面宽26 m的高速公路桥梁，桥梁分幅设计，横断面如图1所示。桥墩桩间距为7.1 m，连接墩支座采用GJZF4400X400X71型四氟滑板橡胶支座，中墩采用GJZ450X600X90型板式橡胶支座。主梁采用C50型号混凝土，桥墩、盖梁、柱间系梁采用C40型号混凝土，桩顶系梁、基桩采用C30型号混凝土。

桥墩立柱主筋采用34根直径28 mm的HRB400钢筋，箍筋采用直径12 mm的HRB400钢筋，箍筋间距为80 mm，净保护层厚度为50 mm。

2 有限元模型

Midas计算模型中，主梁、盖梁、桥墩、桩顶系梁和柱间系梁基桩均采用梁单元进行模拟，板式橡胶支座采用弹性连接，其剪切刚度依据《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）取值[2]。结构有限元计算模型如图2所示。

基桩约束采用节点弹性连接，连接刚度采用《公路桥涵地基与基础设计规范》（JTG 3363—2019）中[m]法计算[3]。

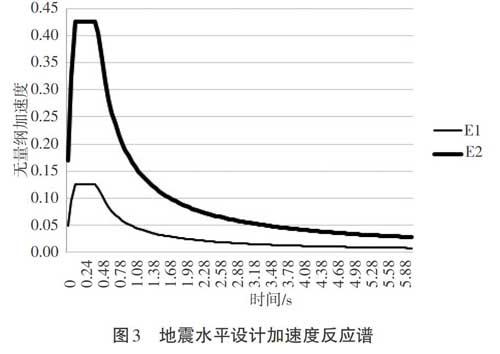
桥位处地震动峰值加速度为0.10[g]，特征周期为0.40 s，场地类型为二类场地。E1、E2地震作用下，水平设计加速度反应谱如图3所示。本研究采用多振型反应谱分析方法，地震作用效用采用CQC方法计算。

3 模擬计算结果及分析

3.1 地震作用下桥墩强度验算

由计算模型的计算结果可知，桥墩最不利截面位于立柱底截面，该最不利截面处在E1、E2地震作用下所受轴力及弯矩如表1所示。

由表1可知，在E1地震作用下，桥墩未进入塑性状态，按照现行的公路桥涵设计规范相关规定验算桥墩的强度，强度满足要求，安全系数约为2.89，表明其具有足够的安全储备。在E2地震作用下，墩柱的压弯强度不能满足要求，墩柱出现塑性铰。在E2地震作用下，人们需要进行墩柱塑性铰区域抗剪强度及墩顶位移验算。

3.2 E2地震作用下塑性铰区域抗剪强度验算

塑性铰区域内顺桥向及横桥向的斜截面抗剪强度的大小取决于塑性铰区混凝土的抗剪能力贡献以及横向钢筋的抗剪能力贡献。塑性铰区域混凝土抗剪强度由墩柱轴压力大小、墩柱体积配箍率、混凝土抗压强度设计值及核心混凝土截面面积等因素决定。横向钢筋抗剪能力受箍筋抗拉强度设计值及箍筋截面面积等因素影响。

根据《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）规定，人们可以得出塑性铰区域内顺桥向及横桥向的斜截面抗剪强度。

钢筋混凝土构件的剪切破坏属于脆性破坏，是一种危险的破坏模式，对于抗震结构，墩柱剪切破坏会大大降低结构的延性能力。由于在E2地震作用下墩柱出现塑性铰，桥墩的弯矩及剪力设计值应按能力保护原则计算。墩柱的剪切强度应大于墩柱可能在地震中承受的最大剪力，对应于墩柱塑性铰处截面可能达到的最大弯矩承载力。

顺桥向墩柱剪力设计值取墩底塑性铰区截面超强弯矩所对应的剪力值，即

[Vc0=MnHn]                          （1）

式中，[Mn]为塑性铰截面超强弯矩，[Mn]=[1.2Mu];[Hn]为墩顶到墩底塑性铰中心的距离。

横桥向双柱式墩墩底及墩顶均可能形成塑性铰，塑性铰区横桥向剪力设计值为：

[Vc0=Mtn+MbnHn]                              （2）

式中，[Mtn]为单柱墩墩顶塑性铰区截面超强弯矩;[Mbn]为单柱墩墩底塑性铰区截面超强弯矩。

表2 塑性铰区抗剪强度验算及构造要求

[塑性铰区抗剪强度 E2作用下/kN 容许值/kN 是否满足规范 纵桥向 421.47 1 541.43 满足 横桥向 789.5 1 541.43 满足 ]

注：最小体积含箍率为0.008 8，设计体积含箍率为0.006 6。

由表2可知，塑性铰区域抗剪强度满足规范要求。由于墩柱较高，墩柱截面较大，箍筋的配置由最小体积含箍率控制。墩柱截面箍筋配置被调整为并置两根直径10 mm的HRB400钢筋，箍筋间距为80 mm，设计体积含箍率为0.009 2，满足相关规范要求[4]。

4.3 E2地震作用下墩顶位移验算

顺桥向墩顶容许位移以单柱墩容许位移验算，其主要受塑性铰区最大容许转角、截面等效屈服曲率以及等效塑性铰长度的影响。顺桥向墩顶容许位移由式（3）计算得出，即

[Δu=13H2×φy+（H-LP2）×θu]                  （3）

式中，[φy]为截面等效屈服曲率;[θu]为塑性铰区最大容许转角;[LP]为等效塑性铰长度;[H]为悬臂墩的高度或塑性铰截面到反弯点的距离。

等效塑性铰长度同塑性变形的发展和极限压应变有很大的关系，依据抗震规范提供的经验公式确定。

截面等效屈服曲率[φy]和极限曲率[φu]等采用弯矩曲率曲线进行计算。利用弯矩曲率曲线进行计算时，混凝土采用Mander模型，钢筋采用双折线模型。

横桥向桥墩为双柱式墩，对于双柱式墩，横桥向很难根据塑性铰转动能力直接给出计算墩顶容许位移的计算公式，横向桥最大容许位移采用Pushover工具进行非线性静力分析，若墩柱的任一截面达到最大容许转角，则即得到桥墩横桥向的容许位移[5]。

由表3可知，在配筋参数修正的情况下，对墩柱进行延性抗震设计时，地震作用下墩柱变形可满足规范要求且具有较大的安全度。

5 结论

针对一联4×30 m T梁桥，根据建立的35 m墩高圆柱式墩有限元模型，本研究采用多振型反应谱法进行了抗震性能验算，主要得到以下结论。在E1地震作用下，桥墩处于弹性工作状态，处于偏压状态的圆柱式墩强度验算满足要求;在E2地震作用下，桥墩出现塑性铰，塑性铰区抗剪强度及墩顶位移均满足相关规范要求。若桥墩高度小于35 m，则桥墩型式可以由方墩优化为圆柱式墩，从而减小桥墩基础尺寸，降低桥梁墩台对沿线原状地形地貌的破坏，贯彻“绿色公路”设计理念。在墩高较大的情况下，塑性铰区顺桥向及横桥向抗剪强度主要受最小体积含箍率控制。

参考文献：

[1]范立础，卓卫东.桥梁延性抗震设计[M].北京：人民交通出版社，2001：20-21.

[2]交通运输部.公路桥梁抗震设计规范：JTG/T 2231-01—2020[S].北京：人民交通出版社，2020.

[3]交通运输部.公路桥涵地基与基础设计规范：JTG T 2231-01—2020[S].北京：人民交通出版社，2020.

[4]范立础，李建中.汶川桥梁震害分析与抗震设计对策[J].公路，2009（5）：122-128.

[5]李建中，宋晓东，范立础.桥梁高墩位移延性能力的探讨[J].地震工程与工程振动，2005（1）：43-48.