基于柔索驱动的锅炉检测机器人轨迹规划研究
2021-07-15洪逸凡谭建平
洪逸凡, 谭建平
(中南大学 机电工程学院,湖南 长沙 410006)
0 引 言
锅炉电厂锅炉管道表面缺陷自动化检测面临着锅炉管道检测区间大、环境复杂等问题,柔索驱动机器人用柔索代替传统刚性构件,使得机器人具有工作区间大,安装简便,机械结构简单的特点,得到了学术界的广泛关注。柔索驱动机器人根据柔索的数目m和动平台的自由度数目n,可以分为欠约束(m
1 平面柔索驱动机器人模型
对于柔索驱动机器人而言,针对不同应用场合其结构设计都会有所不同。本文所研究的用于电厂锅炉管道巡检的机器人是属于平面柔索牵引机器人,具有2个平移自由度。通过对该类型机器人的充分调研,在实验室组建该柔索驱动机器人的缩比实验台,实验台实体结构示意如图1所示。该机器人结构主要包括基础设施、卷筒、伺服电机及驱动器、相机末端平台、运动控制卡、拉绳传感器等。系统共有两个柔索驱动单元,即上两根绳索同时驱动绳索的收放,控制末端相机平台在平面XY方向运动,下两根牵引绳索是由拉线传感器提供,用于获取末端平台精确位置信息和给末端平台提供恒定约束力来防止平台横向摆动。

图1 柔索驱动缩比实验台实体结构示意
将平面柔索驱动机器人的驱动器及末端平台简化为点,其中,P2,P3分别代表两个柔索驱动器单元,P2,P4代表拉线传感器提供的两个柔索被动约束力提供单元。类似地,L2,L3代表两根驱动力柔索,L1,L4代表两根被动约束力柔索。各点坐标如图2标注。
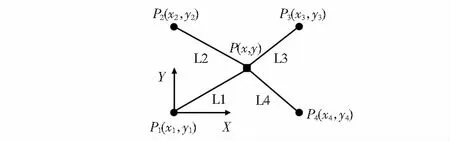
图2 柔索驱动机器人运动学简化模型
2 运动学分析
本文中运动学分析是研究在末端平台运动过程中,其牵引柔索与末端执行器的位置、速度的相互转换关系。
运动学位置分析主要是对柔索驱动机器人末端平台位置与各柔索长度变化进行正逆解分析[7]。假设柔索的刚度是无穷大,不会发生弹性形变,同时也不考虑柔索的弯曲、自重等因素的作用。本文首先通过已知的末端平台P的位置信息,通过运动学位置反解计算出各柔索索长度Li(i=1,2,3,4)。依据图2所示的运动学模型,结合平面两点间距离公式,可得各柔索长度为
(1)
由此可知,如果给定末端平台的轨迹,则任意时刻的末端平台的位置都能唯一确定。
运动学位置正解是根据已知的柔索长度Li求解末端平台位置信息。本文研究的平面柔索驱动只有两个平移自由度,故根据冗余特性,只需联立式(1)中任意两组等式可求解对应末端平台的位置坐标。如图2所示,设P1为坐标系原点,可得x1=y1=x2=y4=0。
假如已知上面两根驱动柔索2和驱动柔索3的长度为L2,L3,以此来求解末端平台位置。根据运动学正解可得
边坡稳定性评价和治理涉及到水利水电工程、铁道工程等诸多工程领域,边坡失稳形成滑坡、崩塌及地裂缝等地质灾害,轻则增加投资、延长工期,重则摧毁建筑物、造成人员伤亡,能否正确评价其稳定性常常是此类工程成败的关键,也是确保工程安全和降低建设费用的重要环节。
(2)
求解上述等式,可以得到末端平台P的坐标
(3)
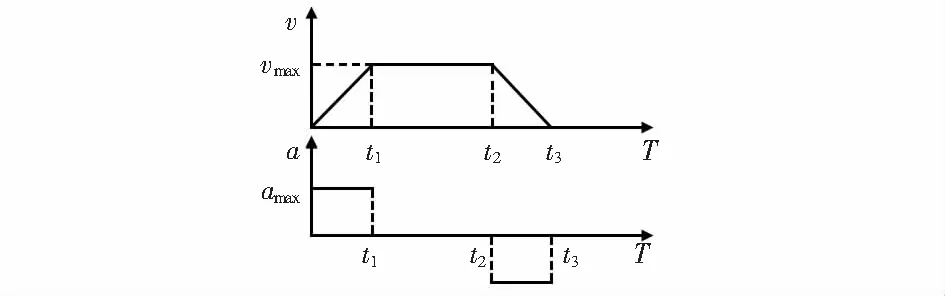
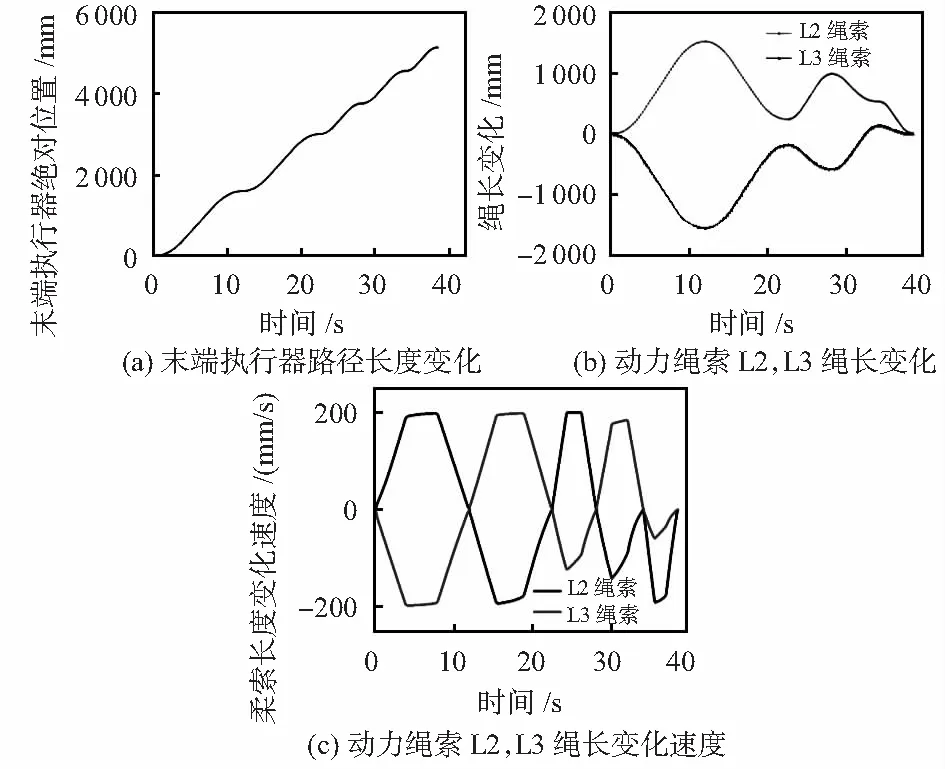
同理,通过已知L4,L3或L1,L3均可求解末端平台P的位置信息。由上面的公式可以看出,求解末端平台的位置坐标即求解两个圆的交点坐标。当两个圆相切,只有一个交点,则末端平台处于工作空间边缘。若两圆相交,根据末端平台位置在工作空间内部,即位置坐标满足约束关系式0 运动学速度分析是研究末端执行器速度与柔索长度变化速度之间的关系。对于本文研究的机构,因为只有L2,L3为驱动力提供绳索,故在本文中主要研究末端平台运行速度与动力柔索长度变化速度的相关关系,为后续轨迹规划提供理论基础。运动速度反解与速度正解过程相反,通过获取末端执行器的速度来求解柔索变化速度。运动学速度反解主要应用偏导数公式,其中i=2,3。求得柔索长度变化的速度通式为 (4) 因此,可知该机器人的动力柔索L2,L3的长度变化速度为 (5) 运动学反解问题可以表示为 (6) 其中 结合式(4)、式(5),柔索L2,L3的长度变化率为 (7) 在对电厂锅炉管道进行巡检时,需要柔索牵引末端平台相机在要求的区域内进行运动轨迹规划,通过机器人的实际工作任务要求,得出末端平台要形成的路径,然后利用运动学反解计算出相应柔索变化信息,这里主要研究运行过程中位置、速度与时间的关系,使得系统能够按照预期的轨迹运动。 在平面柔索机器人巡检过程中,通过点对点直线轨迹规划将工业相机送到指定位置并获取缺陷管道图像,即实现机器人的直线轨迹位置规划和速度规划。假设末端执行器从B1点按照直线轨迹运动到点B2,其中,起始位置点B1的坐标位置为(xb1,yb1),终止位置点B2的位置坐标为(xb2,yb2)。 根据两点式方程及两点间的距离公式,求得直线B1B2的解析式和点B1,B2的距离为 (8) (9) 通过矢量表达式来表示点B1和B2,则点B21为 B21=B2-B1=xb2i+yb2j-(xb1i+yb1j) (10) 单位方向矢量表示为n21=B21/Dis。 当末端平台沿着直线轨迹运行时,假设匀速运行的速度为v,运行总时间为T,在运行中任意t时刻,末端平台的位置矢量表达式为Pt=xti+ytj,则轨迹规划的运动学表达式为Pt=P1+n21vt,t∈[0,T]。 为保证该柔索驱动机器人的末端平台运动轨迹的平滑性,结合柔索驱动的非线性特点,采用梯形速度控制和位置离散微分方法实现对末端平台点对点速度规划。梯形速度控制方法具有结构简单,计算方便等特点得到了广泛应用。标准梯形速度曲线如图3所示。 图3可以看出其对应输出距离s为分段函数,即 图3 梯形速度规划的速度及加速度 (11) 依据式(8)对直线B1B2进行微分,求解各段间动力柔索L2及L3绳长差值ΔL2,ΔL3,依据式(11)末端平台梯形速度规划,反解各区段速度,即可得起始位置点B1到终止位置点B2的运动位置速度时间变化规律,并将数据存入控制系统缓冲区,实现柔索驱动末端执行器点对点直线轨迹运动。 本文中柔索驱动机器人在现场巡检作业时,是以点对点直线轨迹为主,运用前面针对系统结构建立的运动学模型,采用MATLAB软件对机器人的点对点直线轨迹规划实例进行仿真实验计算。设定平面柔索机器人末端点P在XOY平行的平面内,以点P1(200,1 300)mm作为直线轨迹规划中的起始点和结尾点,依次通过点(1 800,1 250),(400,1 150),(1 000,700),(200,700)mm,通过路径规划便可得如图4所示的5段直线路径。运用梯形速度规划算法进行速度规划,运动学反解及位置离散微分进行位置规划。设初速度V0=0 mm/s,最大速度为200 mm/s,加速、匀速、减速时间相等。 图4 仿真直线轨迹规划 解算出末端平台的路径长度变化如图5(a),动力柔索L2及L3的绳长和速度变化如图5(b)和图5(c)所示,在仿真过程中,走完这段轨迹所花的时间为39.1 s。 图5 仿真结果 从图5的仿真结果可以看出,末端平台的路径变化,动力绳索的绳长、速度的变化都比较平稳,说明该轨迹规划算法能够实现末端平台的点对点直线运动的平稳运行及满足本文平面柔索牵引巡检机器人对运动性能的要求。 本文针对工业自动化检测的迫切需求,创新性地引入了基于平面柔索驱动的检测机器人,对其点对点直线轨迹规划算法深入研究。仿真结果证明:所研究的柔索驱动机器人能较好地实现轨迹跟踪,保证机器人在整个作业过程中运行平稳、连续、定位精度等能满足工业检测作业要求。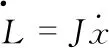
3 轨迹规划算法
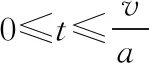
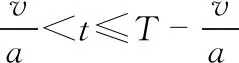
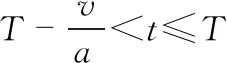
4 仿真结果与分析

5 结 论
