基于LINGO的大钩弹簧优化设计

段树军 ，王潇潇 ，廖春林 ，游娜 ,2，王浩宇 ，赵锐

（1.宝鸡石油机械有限责任公司，陕西 宝鸡 721002；2.中油国家油气钻井装备工程技术研究中心有限公司，陕西 宝鸡 721002）

0 引言

大钩是石油钻机游吊系统中重要的提升设备，在钻井及下套管作业时承受下部钻柱或套管柱重力。大钩结构图如图1所示。大钩吊环与游车的提环接触，吊环与吊环座通过两个提环销连接，钩杆从吊环座的顶部穿入，钩杆螺母与钩杆通过螺纹连接，钩体是铸造结构，钩体上设置有主钩和副钩，主钩可以悬挂水龙头，两个副钩悬挂吊环，钩体通过左旋梯形螺纹与下筒体连接，当钩体受载时，钩体与下筒体下移压缩内、外弹簧，当弹簧压缩到位以后，下筒体坐在钩杆螺母的顶部大端面，将载荷依次传递给钩杆、吊环座及吊环。

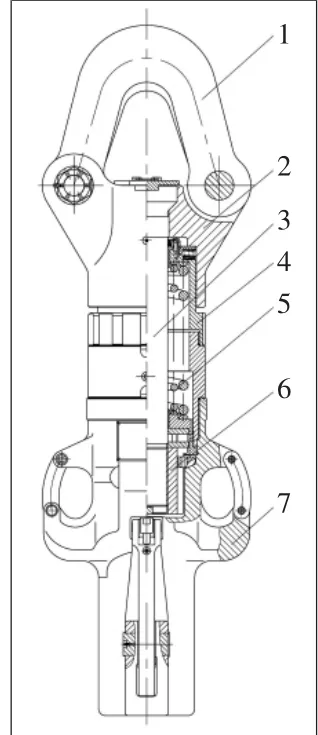
图1 大钩结构示意图

目前对大钩的研究主要集中在大钩及其承载部件的可靠性分析上，相关专家学者使用有限元分析软件对吊环座、钩体等进行了有限元分析[1-2]，大钩作为钻机游吊系统的核心部件，安装在大钩内的弹簧工作时承受较大载荷，且弹簧的安装尺寸受限，为使弹簧在满足性能的前提下达到安装尺寸最小的目的，本文使用LINGO语言结合大钩结构对大钩弹簧进行设计优化。

LINGO语言主要用于求解线性规划、非线性规划等问题，可以较方便地求解工程中较为常见的整型优化问题，无需输入初始参数，具有执行速度快，易于输入、求解等优点，在工程领域得到了较为广泛的应用。

1 大钩弹簧方案分析

通常当设计承受载荷较大且安装空间受限制的圆柱螺旋压缩弹簧时，可以采用组合弹簧设计，通过对大钩结构进行研究不难发现，大钩的弹簧安装在上、下筒体及钩杆的环形空间内，安装空间较小，且作为钻机游吊系统大钩要承受较大载荷，因此钩体内安装的内、外弹簧设计为一组同轴并联的双圆柱螺旋压缩弹簧，为了保证内、外弹簧的同心关系，防止内、外弹簧产生歪斜，两个弹簧的旋向应当相反[3]，通常情况下外弹簧是右旋，内弹簧是左旋，大钩在进行装配时，内、外弹簧被预压缩，在进行钻井作业时，当大钩悬吊下部钻柱时，弹簧被进一步压缩，而在进行起钻作业时，这组内、外弹簧能使立根松扣后向上弹起，当筒体内装有润滑油后，可借助缓冲机构消除钩身上下运动时产生的轴向冲击，消除卸扣时钻杆的反弹振动使钻杆接头螺纹不受损坏。

2 内、外弹簧优化设计的数学模型

双弹簧优化设计的结构如图2所示，图2中：d1为外弹簧的簧丝线径；d2为内弹簧的簧丝线径；D1为外弹簧的弹簧中径；D2为内弹簧的弹簧中径；Do1为外弹簧的外径，Do1=D1+d1；Do2为内弹簧的外径，Do2=D2+d2；DI1为外弹簧的内径，DI1=D1-d1；DI2为 内 弹 簧 的 内 径，DI2=D2-d2；δr为外弹簧和内弹簧径向之间的间隙，δr=（D11-Do2）/2；Pn为内、外弹簧承受的载荷。

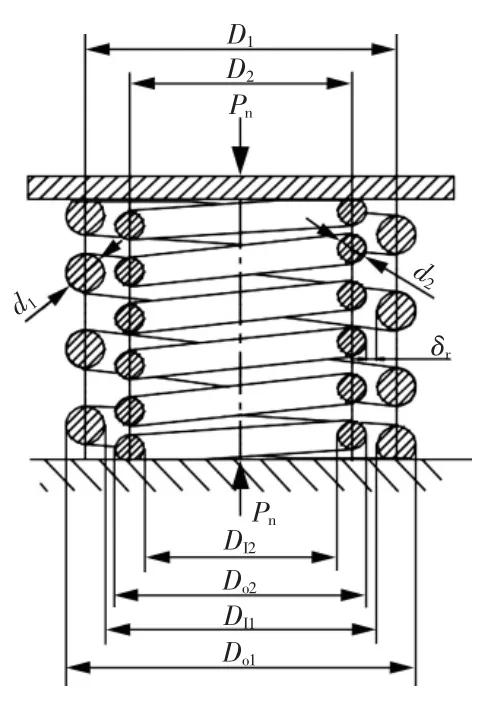
图2 双圆柱螺旋弹簧结构

内、外双圆柱螺旋压缩弹簧的结构是两个弹簧的并联结构，并联弹簧的刚度为k=k1+k2，即内、外两个弹簧共同承载工作载荷。

2.1 确定设计变量

圆柱螺旋压缩弹簧的参数一般包括簧丝线径、弹簧中径、有效圈数、旋绕比、弹簧刚度等，在进行弹簧设计时，一般选取簧丝线径d、弹簧中径D、有效圈数作为设计变量，大钩弹簧因为采用内、外弹簧并联结构，组合弹簧的外弹簧载系数为μ，则外弹簧的最大工作载荷为μPn，内弹簧的最大工作载荷为（1-μ）Pn，因此大钩内、外弹簧优化设计的设计变量为

式中：d1为外弹簧的簧丝线径；d2为内弹簧的簧丝线径；D1为外弹簧的弹簧中径；D2为内弹簧的弹簧中径；n1为外弹簧的有效圈数；n2为内弹簧的有效圈数；μ为外弹簧的载荷系数。

若根据推荐的外弹簧和内弹簧最大工作载荷之比为5:2[3]，则设计变量变为6个，本文将此方案设计值作为对比参考。

2.2 确定目标函数

大钩的内、外弹簧安装在筒体及钩杆的环形空间内且要承受较大载荷，这属于双弹簧的典型应用场合，在满足弹簧性能要求的前提下，以弹簧的体积最小作为优化的目标函数:

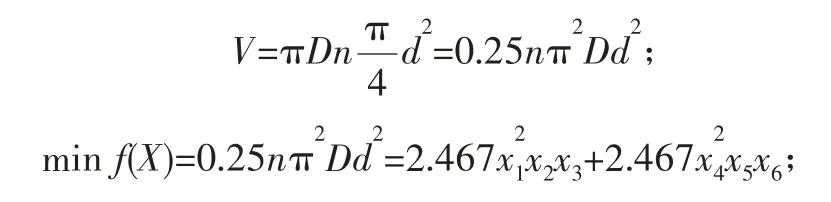
X=［x1，x2，x3，x4，x5，x6，x7］T=［d1，D1，n1，d2，D2，n2，μ］T。

2.3 确定约束条件

1）弹簧的最大剪应力应满足[4]

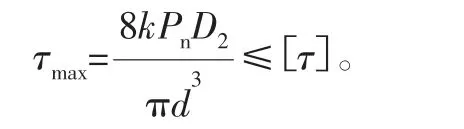
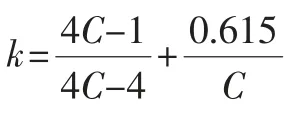
可得约束条件：

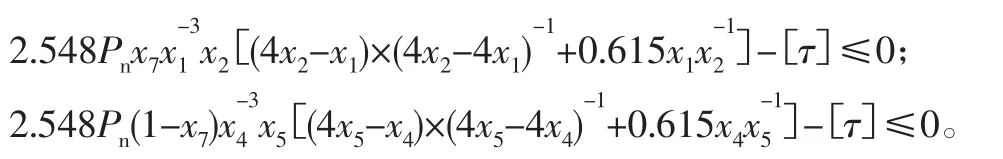
2）设计要求弹簧在最大压缩变形量λmax时产生的载荷即为最大工作载荷Pn：

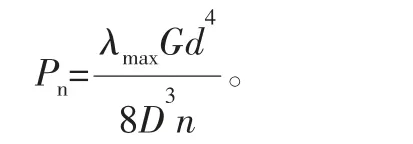
式中：G为弹簧材料的切变模量，Pa。

可得约束条件：

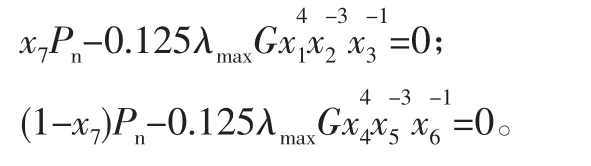
3）弹簧的旋绕比有一定的取值范围：

Cmin≤C≤Cmax。

式中：C为弹簧的旋绕比，C=D/d，Cmin=4，Cmax=14。

可得约束条件：

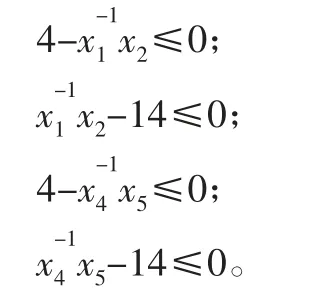
4）弹簧的径向间隙应该满足:

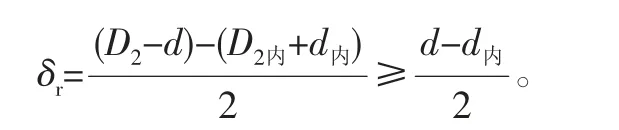
可得约束条件：

2x1+x5-x2≤0。

5）内、外弹簧应该能够装入下筒体和钩杆之间的空间中，可得约束条件：

x1+x2≤Dmax；

x4-x5≤-Dmin。

因大钩弹簧主要作用是使立根松扣后向上弹起，大钩弹簧载荷变化频率较低，且大钩钩身内注入的油通过弹簧座油孔流动作为阻尼耗散振动系统能量，此处不将大钩弹簧不发生共振作为约束条件。

3 优化实例及结果分析

本文以某型号大钩的内、外弹簧来进行优化设计，弹簧在装入大钩的过程中首先被预压缩，大钩工作行程是200 mm，设计最大压缩量为440 mm，这组内、外弹簧能够使立根松扣后向上弹起，考虑大钩部分零件及一个立根的质量，弹簧最大工作载荷Pn=7.2×104N，内、外弹簧的材质均为60Si2MnA，材料的许用切应力为710 MPa，剪切弹性模量为7.85 G Pa。结合该型号大钩的钩杆外径及下筒体内径的设计尺寸，Dmax=355 mm，Dmin=180 mm，

根据以上约束条件，建立内、外弹簧的优化数学模型为：

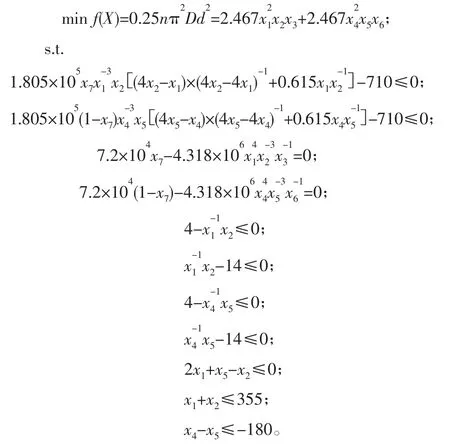
通过LINGO语言设计程序进行此优化模型的计算并得到优化结果，相同设计条件下的内、外弹簧结构的优化设计结果比对如表1所示，从表1可知，内、外弹簧结构优化设计后得到的弹簧组体积比对比值减小了4.4%。

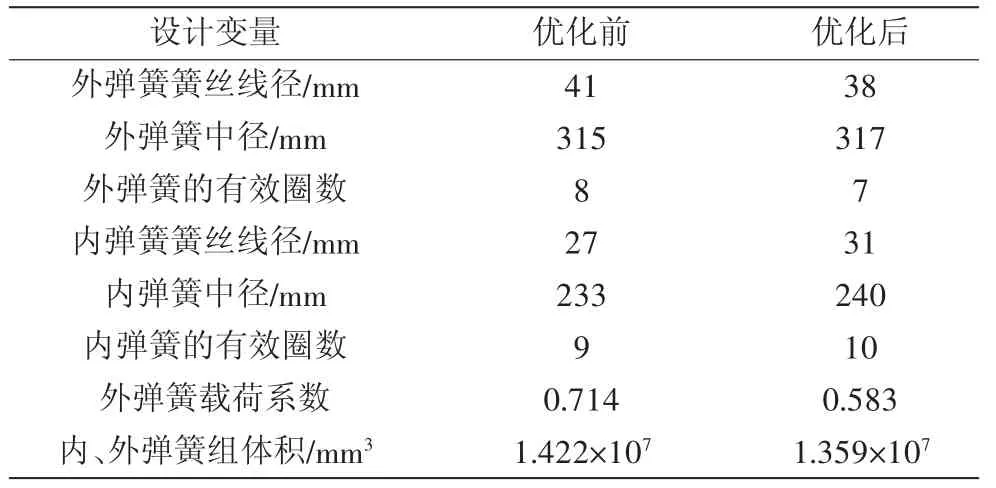
表1 优化前后结果对比

根据计算结果结合机械设计手册选定大钩外弹簧簧丝线径为φ40 mm，中径为φ315 mm，有效圈数为7圈，内弹簧簧丝线径为φ30 mm，中径为φ235 mm，有效圈数为10圈。

4 结论

1）使用LINGO语言求解机械优化设计问题非常方便，其参数输入简单明了，编程工作量小，求解效率高，能够得到满足工程要求的解，可以大幅提高设计效率。

2）大钩内、外弹簧结构属于典型安装空间受限且承受较大载荷的场合，对大钩内、外弹簧进行结构优化，可以使弹簧在满足设计条件下更好地适应受限空间。