指向数学核心素养的任务设计
——以球面距离教学为例
2021-07-15周宁医
周宁医
(上海市浦东教育发展研究院 200127)
1 引言
随着《普通高中数学课程标准(2017年版)》(以下简称《数学课程标准》)的颁布,一个迫切需要研究的问题显现出来,就是如何在课堂教学层面上培养学生的数学核心素养?与之前的课程标准相比较,新的课程标准在指导思想、课程理念、教学方式、教学评价等方面发生了变革,要使新的课程改革真正落实,课堂教学的研究必须先行.
《数学课程标准》提出了6个数学核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析,并且规划好了路线图:反映数学学科核心素养的四个方面,它们分别为“情境与问题”、“知识与技能”、“思维与表达”、“交流与反思”;聚焦数学学科核心素养的四个主题,它们分别为函数、几何与代数、概率与统计、数学建模活动与数学探究活动;评价数学学科核心素养的三个水平[2].美好的蓝图需要依托日常教学的呈现来达到培养数学学科核心素养之目的.数学核心素养是在学习过程中形成的,不能脱离内容与过程.教师应该明确不同的学习主题对核心素养的培养有所侧重.如:几何与代数主题,重点提升的是直观想象、逻辑推理、数学运算和数学抽象素养;概率与统计主题,重点提升的是数据分析、数学建模、逻辑推理和数学运算素养.可见,主题和六个方面的数学核心素养之间并不是一一对应的关系.了解了这些特点,教师就需要深入研究数学核心素养达成的任务设计,只有这样,才能提高教学的针对性,实现精准培养.
“指向数学核心素养的任务设计”类似于项目学习:一是把握数学内容的本质;二是创设适合的教学情境(包括现实情境、数学情境、科学情境等),提出合理的问题,引导学生学习相应的数学理论(中学数学课本范畴内的概念、公式、法则等);三是启发学生独立思考,鼓励学生参与集体交流;四是让学生在掌握数学知识和技能的同时,感悟数学的本质,让学生在积累数学思维经验中,逐步习得数学核心素养.
本文以“球面距离”教学为例,呈现“指向数学核心素养的任务设计”的过程.笔者认为,以课堂教学为阵地,以数学内容为主线,以情境与问题、知识与技能、思维与表达和交流与反思为路径,在润物细无声处培育数学核心素养.
2 情境与问题
(1)情境
人民网约翰内斯堡2015年10月30日电,2015年是南非的“中国”年,当地时间10月30日上午8点10分,迎着非洲大陆最南端美丽的晨曦,中国国际航空股份有限公司北京—约翰内斯堡CA867/B2035次首航航班波音777-300ER“微笑中国号”平稳地降落在约翰内斯堡奥利弗·雷金纳德·坦博国际机场,标志着中国国航开通北京至约翰内斯堡这条新航线首飞成功.
航班号为CA867/B2035的波音777-300ER型客机于北京时间10月29日23时15分从北京首都机场起飞,于次日当地时间7时35分到达约翰内斯堡奥利弗·雷金纳德·坦博国际机场.
(2)问题
如何设计从北京直飞约翰内斯堡的最近航线.
3 知识与技能
3.1 知识
平面上的两点之间线段最短,该线段的长度就是两点之间的距离.类似地,要定义球面上两点之间的距离,也应该在球面上找到联结两点的最短距离,该路径长度就是球面上两点之间的距离.可以证明,在联结球面上两点的路径中,通过该两点的大圆劣弧最短,因此该弧的长度就是这两点的球面距离[3].
3.2 技能
例1已知地球的半径约为6371千米,上海的位置约为东经121°27′,北纬31°8′,台北的位置约为东经121°27′,北纬25°5′,求两个城市之间的距离(结果精确到1千米)[4].
解:因为上海和台湾在同一经线上,所以它们在地球的同一个大圆上.设地球的球心为O,上海、台北分别为点A、B,由上海、台北的经度知,∠AOB=6°3′,地球半径r=6371千米.可计算得AB的弧长


所以上海和台北两个城市之间的距离约为672千米.
例2已知北京的位置约为东经116°,北纬40°,纽约的位置约为西经74°,北纬40°.求两个城市之间的距离(结果精确到1千米)[5].

分析:虽然北京和纽约在同一条纬线上,但这条纬线并不是地球的大圆,所以要找到通过北京和纽约的大圆.

由已知条件知
∠AOC=∠BOC=40°,
∠COD=360°-(116°+74°)=170°,
地球半径r=6371(km).
由余弦定理得

AB2=CD2
=OC2+OD2-2OC·OD·cos ∠COD,

其中OA=OB=r,OC=OD=rcos 40°.

所以北京和纽约两个城市之间的距离约为11062千米.
4 思维与表达
4.1 整理思维
通过上述两例学习,已初步掌握了地球上同经度或同纬度两点的球面距离计算.那么,地球上任意两点的球面距离如何计算呢?
4.2 数学建模
一般地,设地球上不同两点A,B,点A的经度为α、纬度分ψ,点B的经度为β、纬度为φ,地球半径为R,试求A,B两点的球面距离.
为了方便表达,约定东经、北纬为正角,西经、南纬为负角.
如图,取球心O为原点,经度为0°的大圆与赤道平面的交线为x轴,赤道平面内过球心O且与x轴垂直的直线为y轴,过球心O与北极N的直线为z轴,建立空间直角坐标系,则点A,B的球面坐标分别为:
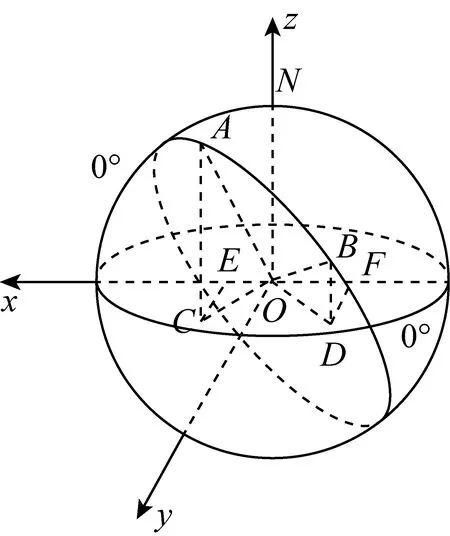
A(R·cosψ·cosα,R·cosψ·sinα,R·sinψ),
B(R·cosφ·cosβ,R·cosφ·sinβ,R·sinφ).
所以
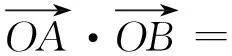
=R2[cosψ·cosφ·cos(α-β)+sinψ·sinφ].
设∠AOB=θ,

=cosψ·cosφ·cos(α-β)+sinψ·sinφ,


cos(α-β)+sinψ·sinφ].
其中,当|α-β|≤π(180°)时,则取|α-β|;当|α-β|>π(180°)时,则取2π-(|α-β|)(或 360°-|α-β|).
推论1当A,B两点同经度时,则α=β,

cos(α-α)+sinψ·sinφ]
=R·arccos(cosψ·cosφ+sinψ·sinφ)
=R·arccos[cos(ψ-φ)]



例1属于此类型.
推论2当A,B两点同纬度时,则ψ=φ,

=R·arccos[cos2φ·cos(α-β)+sin2φ]

例2属于此类型.
4.3 问题解决
4.3.1 信息收集
根据中华地图学社提供,北京首都机场位于:东经116°36′,北纬40°5′,翰内斯堡奥利弗·雷金纳德·坦博国际机场位于为:东经28°14′,南纬26°8′.
查阅360百科知,民航客机起飞和降落阶段处于对流层,在平流层都是巡航阶段,也是飞机平飞阶段,民航客机一般巡航在一万米左右高空,飞行速度一般为900 km/h左右.
4.3.2 基本假设
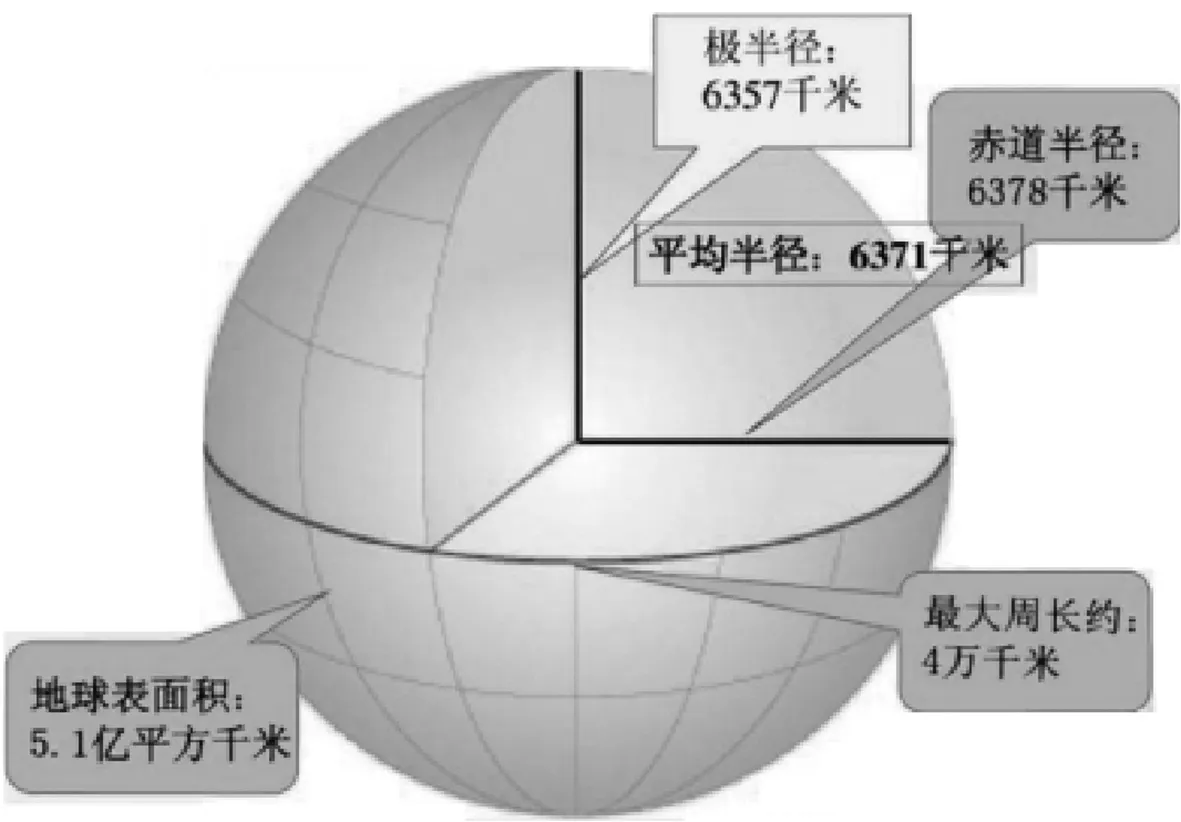
(1)在中学视域下,把地球抽象成一个球体(实际上地球是一旋转椭球体,赤道半径为6378km,极半径为6357km),地球自转因素不考虑.
(2)假设飞机在飞行过程中速度变化不大,看作匀速飞行.
(3)假设飞机飞行高度恒定,始终为距地表10千米.
(4)假设飞机正常飞行,不会发生突发事件以及天气变化等.
4.3.3 模型运用
根据收集到的信息:北京首都机场坐标B(116°36′,40°5′),约翰内斯堡奥利弗·雷金纳德·坦博国际机场坐标Y(28°14′,-26°8′),飞机巡航高度h=10千米,地球半径R=6371千米,飞机巡航时沿大圆半径H=R+h=6371+10=6381千米飞行,飞行速度v= 900 km/h.代入模型:

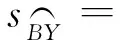
cos(116°36′-28°14′)-sin 40°5′·
sin 26°8′]

≈11728(千米),

所以,从北京首都机场到约翰内斯堡奥利弗·雷金纳德·坦博国际机场的飞行时间大约需要13个小时.
5 交流与反思
5.1 误差分析
根据人民网报道:航班号为CA867/B2035的波音777-300ER型客机于北京时间10月29日23时15分从北京首都机场起飞,于次日当地时间7时35分到达约翰内斯堡奥利弗·雷金纳德·坦博国际机场(北京与约翰内斯堡时差6小时).
也就是说,航班号为CA867/B2035的波音777-300ER型客机,从北京直飞约翰内斯堡奥利弗·雷金纳德·坦博国际机场用时14小时20分钟.根据球面距离计算模型计算,从北京首都机场直飞约翰内斯堡奥利弗·雷金纳德·坦博国际机场,大约需要13个小时,之间还相差1小时20分钟.
根据球面距离计算模型,计算的是北京首都机场万米高空处到约翰内斯堡奥利弗·雷金纳德·坦博国际机场万米高空处的飞行时间.事实上,飞机在机场跑道上滑行加速,然后仰冲飞行穿过对流层进入平流层巡航,飞机在对流层的速度是小于在平流层的速度;同理,飞机在到达目的地前需要俯冲飞行穿过对流层降落在机场跑道上,滑行减速后才停住.坐过飞机的人都知道,飞机在到达目的地前30分钟开始俯冲下降.
根据以上分析,准确地说,从北京到约翰内斯堡的时间 = 滑行加速时间 +仰冲时间 + 巡航时间 + 俯冲时间 + 滑行减速时间,因此,球面距离计算模型所计算的时间为巡航时间.
所以按球面距离计算模型设计从北京直飞约翰内斯堡的航线是可信的.
5.2 模型反思
球面距离计算模型,默认了球面距离定义中“在联结球面上两点的路径中,通过该两点的大圆劣弧最短”的事实,事实果真如此吗?还有待于证明.

证明如图,联结OO1,O1A,O1B,OA,OB,取AB的中点C,联结O1C,OC,则O1C⊥AB,OC⊥AB.

(1)当a 设∠AO1C=α,∠AOC=β, (2)当a=R时,显然,L1=L. 故球面距离定义中“在联结球面上两点的路径中,通过该两点的大圆劣弧最短”成立. 《数学课程标准》提倡引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界.本课题的任务设计是基于对生活实际问题的思考,揭示学习“球面距离”的必要性.受平面上两点之间距离定义的启发,类比想象曲面上两点之间距离的定义方法,在体验与感悟中学习知识、掌握技能、培养能力.通过对解题思维的整理,引发深度思考,从而寻找球面上任意两点之间距离的计算方法,进而系统地开展数学建模活动.数学建模过程,需要有丰富的想象、直观的抽象、缜密的思考、严格的推理、准确的运算、信息的处理等作为基础,才能建立可靠的模型.在运用球面距离计算模型解决实际问题时发现:理想状态与实际情况存在偏差、要注意建立数学模型的条件等,这些都需要做出合理的解释和必须的证明. 因此,经历“情境与问题”、“知识与技能”、“思维与表达”和“交流与反思”的过程是培养数学核心素养的基本方法和路径.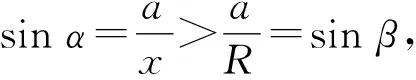






6 后语
