基于数学核心素养的数学科学精神培养的课例研究

李织兰 蒋晓云

(桂林师范高等专科学校 541199)

《中国学生发展核心素养》提出以培养“全面发展的人”为中心，分为“文化基础、自主发展、社会参与”三个方面，综合表现为六个素养：人文底蕴、科学精神、学会学习、健康生活、责任担当、实践创新.

科学精神是学生成长的需要，是与数学关系最为密切的核心素养.数学的科学精神是数学课程在促进学生终身发展中独特价值体现的标志,它应包括三个方面：(1)崇尚真知(2)理性思维(3)勇于探究.

我们立足于中学数学课堂实践,通过课例研究着力探讨培养中学生数学的科学精神培养的策略和路径.

1 核心素养下的数学科学精神的内涵

数学素养是学生在数学学科内所具有的基本专业素质，这些素质是通过长时间的数学专业训练所形成的数学思维，通过这种思维促成“四基”(积累数学基础知识，掌握数学基本技能，感悟数学思想方法，形成数学活动经验)的落实，数学素养可以分为三个层次：

一是表层知识，包括数学概念、数学结论(性质、法则、公式等)等基础知识和测量、计算、作图等基本技能.

二是深层知识，包括数学基础知识与基本技能所承载的基本的数学思想方法.

三是数学精神，体现为数学思想、数学史观、数学审美等，让学生在现实与历史中建构数学，形成数学科学精神.

三个层次的内容相互融合交织，我们把数学当作“日常生活的工具”，关注数学对人类物质生活所带来的影响；把数学当作“思维的体操”，重视数学对人的思维方式的影响；我们把数学当作“科学精神”，重视数学对人类精神方面的巨大作用.

克莱因认为：“数学是一种精神，一种理性精神.” 我国数学家齐民友先生认为数学精神是“彻底的理性探索精神”.

在中学数学课程的教学中，努力寻找可以进行数学科学精神渗透的契机，把学生在数学学习中亲身经历过的数学问题探究过程作为教学情境，让知识构建的过程变得更加圆润，积极地培育理性精神：理性思辨，不感情用事；实事求是，不盲从权威；尊重数据，不弄虚作假；科学严谨，不随欲而为.落实立德树人、学科育人的根本任务.

2 数学精神培养的课例研究

我们立足于中小学数学课堂实践,从数学科学精神培养的教学实践角度出发，通过课例研究着力探讨培养中学生数学的科学精神培养的策略和路径，形成了一批课例[1-8]，例举之一如下.

案例：探索勾股定理，培养致善精神

勾股定理是初中数学课程的核心内容之一，历来是教学改革的风向标.“勾股定理”是经过无数初中教师演绎过的一节典型课例，为什么我们要花这么大的力气来研究这一节课，这是因为：勾股定理是漫漫数学长河中一个非常重要的定理，只要说到勾股定理，我们总会想到“商高”、“勾三股四弦五”、“毕达哥拉斯”、“赵爽弦图”、“出入相补”……勾股定理的研究过程彰显了古今中外研究者的数学精神.其证明方法也极其多样化，体现了各国数学家们孜孜不倦的钻研精神.

本节课选自人教版初中数学八年级下册第18章第1节“勾股定理”的内容.我们以发现和证明勾股定理的各种几何方法为主线，深入钻研教材，梳理出勾股定理发展的一个历史线，以勾股定理发展的历史文化背景为暗线贯穿整堂课始终.借助勾股定理丰富的文化背景，着力培养学生的人文底蕴和科学精神.

在我国古代，人们将直角三角形中短的直角边叫做勾，长的直角边叫做股，斜边叫做弦.《周髀算经》是我国最古老的一部数学著作，在唐代时被定为国子监算学科必修的十部算经之一.书中开头记载约公元前 1120 年的商高与周公的一段关于怎么度量天地之间的距离的一段对话：故折矩，以为勾广三，股修四，径隅五，即“勾三股四弦五”.

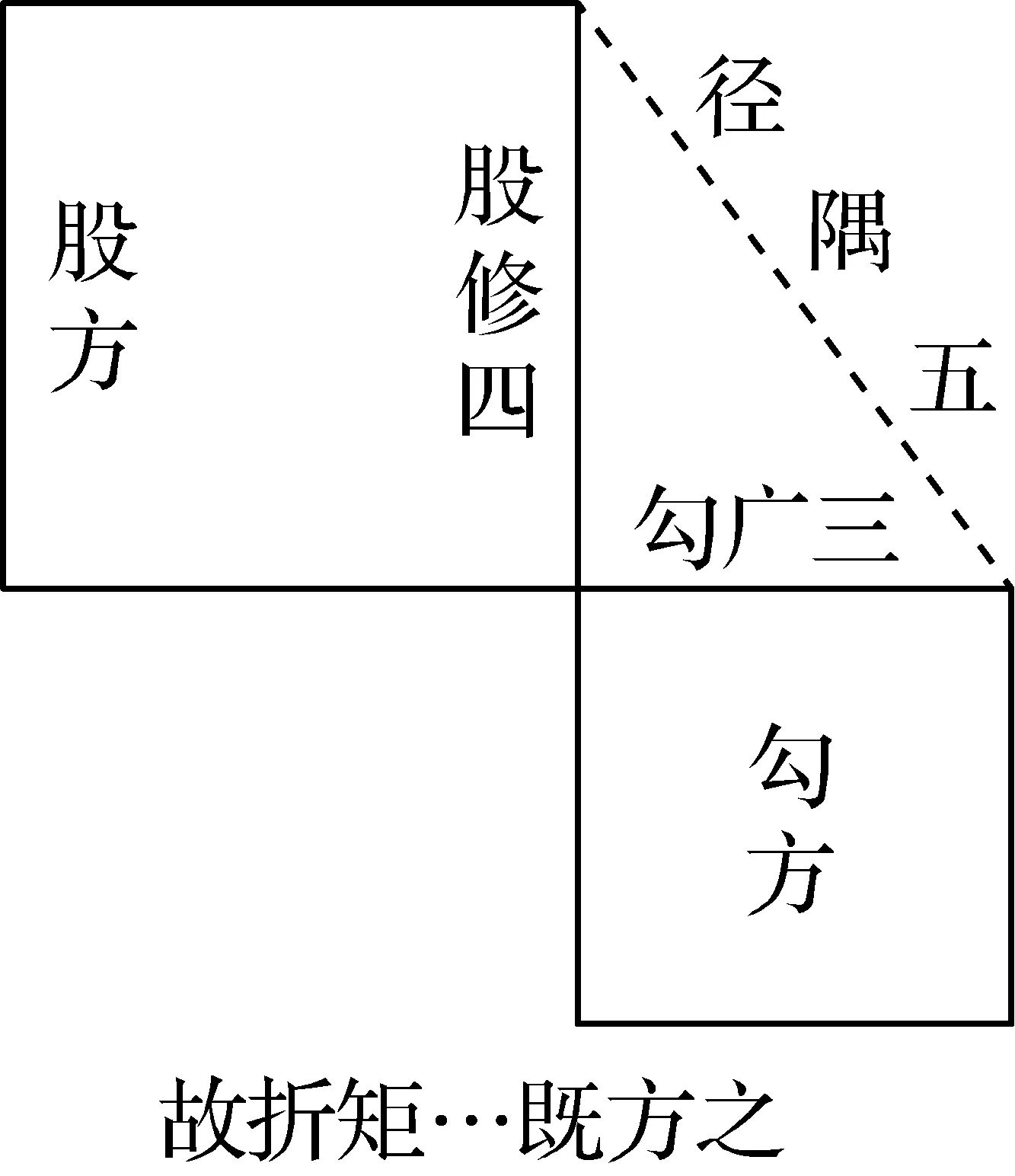
也就是说在约三千多年前，人们已经知道：如果勾是三，股是四，那么弦是五.商高发现了勾股定理中的一个特殊例子.特例以外还有无穷个直角三角形不能用“勾三股四弦五”来求解.

相传2500年前，毕达哥拉斯有一次在朋友家做客，他在欣赏美丽地砖图案的时候发现：两个小正方形的面积和等于这个大边长正方形的面积.

毕达哥拉斯发现等腰直角三角形的这一特殊性质之后，还研究了很多不同类型的直角三角形，归纳发现：任意直角三角形两直角边的平方和等于斜边的平方.

我们跟随毕达哥拉斯的脚步，一起来做实验探究一般的直角三角形的三边数量关系.

学生活动：首先在方格纸上任意画出直角三角形，以三边分别向外作了三个正方形，通过计算各正方形的面积，来验证三边的平方关系.

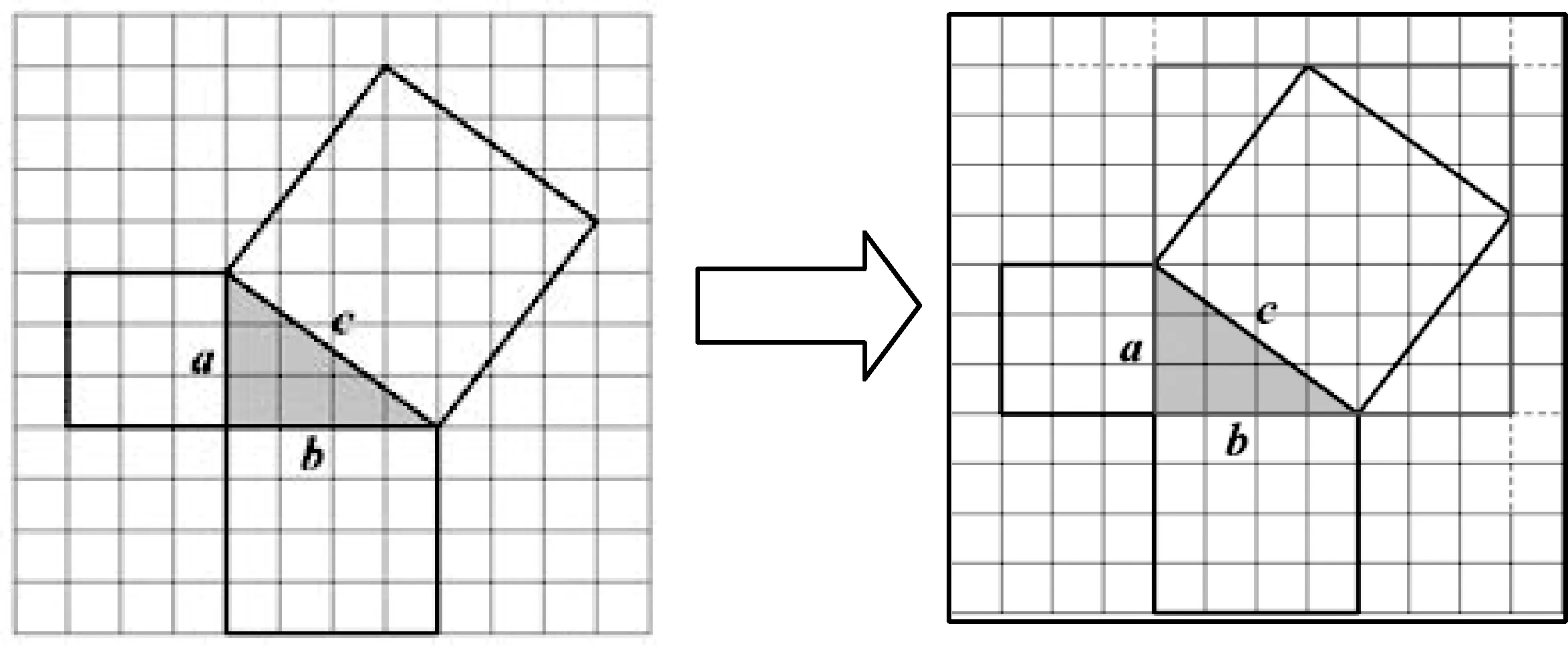
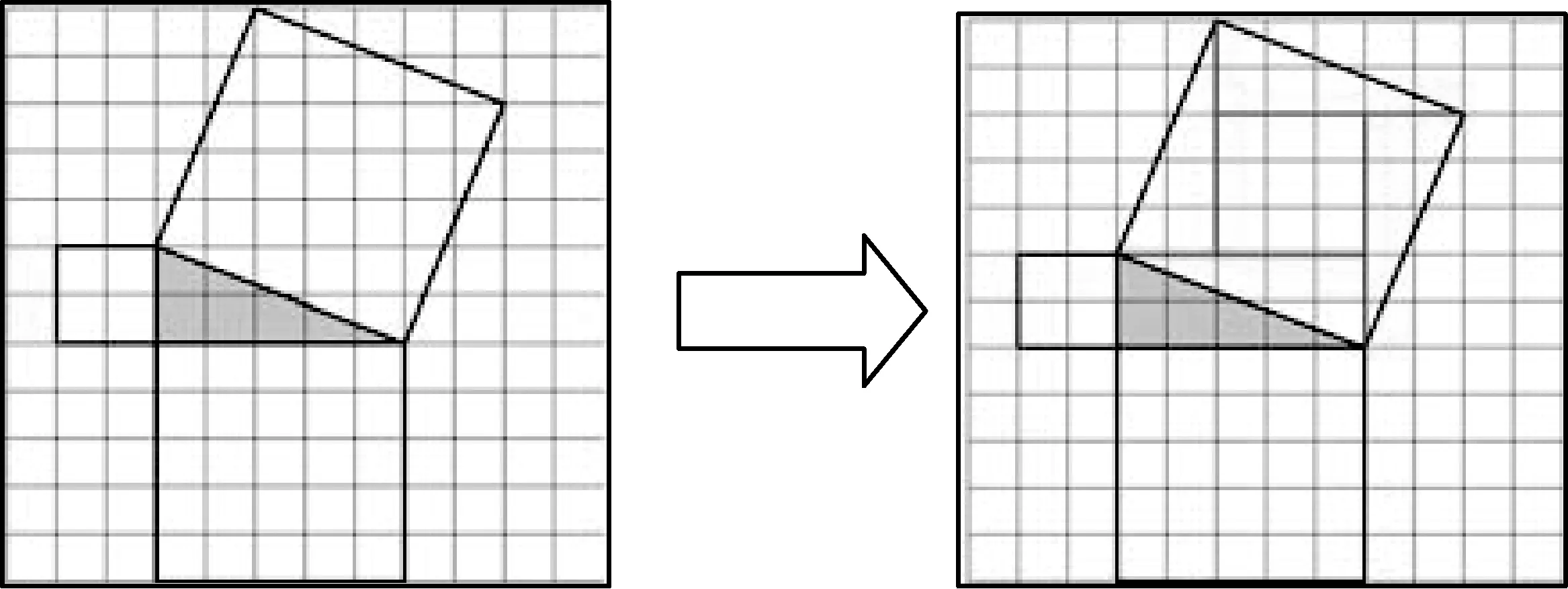
一位同学展示他的计算方法，如图，直角边上的正方形的大小可以用“数小方格”的方法得到，还可以这样求斜边上正方形面积：过斜边上正方形的四个顶点作一个大正方形，边长为a+b.它包含四个与原三角形全等的三角形和斜边上的正方形.所以，斜边上正方形面积等于大正方形面积减去四个三角形面积，即

还有同学展示了他们不同的验证方法.

学生在方格纸上作图验证这个过程中，用面积法验证平方关系，巩固求面积常用的割补法.感悟特殊到一般归纳思想，思考并理解怎样才能使问题一般化.初步感受构造法是证明问题的一种思路，为赵爽弦图证明勾股定理作铺垫.

数学以其严谨、严密、客观，让人们对其怀有尊重和信任.数学“求真”不轻信实验、观察、归纳，实践中发现的数学结论必须经受极为严格的逻辑检验(即数学证明)，才能成为定理.欧几里得的《几何原本》就是用公理化思想和严密的逻辑建立数学体系，开创了理性文明的先河，数学成为一门演绎的学科.

实验验证还不能算严格的证明，因为方格纸具有特殊性，实验归纳得到的结论可能是正确的，也可能是错误的.想要获得一般性的结论，在一般的平面上对一般的直角三角形进行说明.

赵爽约在 222 年创作了一篇“句股圆方圆说”论文，他画了一张“弦图”表述勾股定理并给出了一个绝妙的证明：“句股各自乘，并之为弦实，开方除之即弦.案：弦图又可以句股相乘为朱实二，倍之为朱实四，以句股之差自相乘为中黄实，加差实，亦成弦实.”

赵爽将勾股定理一般化成了真正的勾股定理，证明有图为证，永载史册.

教师直接展示赵爽弦图的证明思路，每一个直角三角形称为“朱实”，中间的一个正方形称为“中黄实”，以弦为边的大正方形叫做“弦实”.

赵爽证明勾股定理的这个方法可谓精妙，为代数和几何紧密结合、互不可分的独特风格树立了一个典范.后来的刘徽把它总结为“出入相补原理”，具有科学创新的重大意义.这个方法被哈佛大学教授库里奇称为“最省力的证明”.

通过中国古代数学证明勾股定理的璀璨明珠——赵爽弦图的介绍，了解我国古代数学家对探索勾股定理作出的贡献，是我国古代数学的骄傲，正因为此，“赵爽弦图”被选为2002年国际数学家大会会徽，现在这个标志也成了中国数学会的标志.感悟古人的智慧，增强民族自豪感，培养爱国主义精神.

3 培养学生科学精神的途径

数学精神是几千年来人们在数学探索过程中积累的精神财富，科学精神是学生成长的需要.培养科学精神是数学教育的核心任务之一，数学课堂的灵魂.下面就如何在中小学数学教学中培养学生的科学精神谈谈我们的一些做法.

3.1 循大师足迹，悟数学文化，培养数学精神

数学精神是几千年来人们在数学探索过程中积累的精神财富，通过渗透数学史、融入数学文化等途径培养学生的数学精神.一代代前人的皓首穷经，为后世挖掘出数学中无尽的珍宝.数学大师们在生活中发现和思考，创造出一个又一个精妙的方法，用不懈的探索精神将数学推向一个又一个高峰.

在数学教学中，精心设计教学，让学生沿着历代数学大师的足迹，复现数学大师的思维过程，使之得到启迪，进而根据自己的体验，用自己的思维方式，“再创造”数学，形成科学精神.

3.2 逻辑推理，数学证明，铸就理性精神

理性的“演绎推理”、“数学证明”比起感性的“合情推理”、“实验归纳”困难得多，如果学生不愿意学习困难的“数学证明”，这会造成学生理性精神缺乏，理性思维能力不强，无法深入地学习数学.

姜伯驹院士早就指出：不证明，数学课就失去了灵魂.欧氏几何中的数学证明，使我们接受了理性精神的启蒙的.通过一些“测量会产生误差”“从特殊到一般归纳不一定完全”和“眼见未必为实”的例子，让学生明白“为什么要证明”.平时数学学习中，增强学生演绎推理的意识，学会数学证明方法，养成要有“说理”的良好习惯，发展理性思维，铸就理性精神.

3.3 质疑反思，理性批判，崇尚求真致善

鼓励学生质疑：教材一定是“权威定论”吗？老师讲的都是“金口玉言”吗？不能仅听老师讲，要学会用大脑去分析和思考，需要敢于质疑的精神.不仅质疑“正确与否”，还应该质疑“课本的方法是最简单方法吗？”“教师讲的是最好的方法吗？”“这种解决问题的方法能否应用更广泛的领域，解决更多的问题？”“条件不变的情况下,能否得出更深刻的结论？”等等，追求的“更普遍的真理，更广泛的应用，更简捷的表达、更美丽的形式，更精确的结果……”，培养致善精神.