数学推广：概念、特征及教育价值①

刘成龙 余小芬

(四川省内江师范学院数学与信息科学学院 641100)

推广是数学研究的重要手段，数学自身的发展在很大程度上依赖于推广.[1]从数学的发展历史来看，数学研究者们总是在已有知识的基础上，通过推广不断向未知的领域扩展.这一过程中，许多数学结果的发现都归因于“幸运的推广”[2]，比如：大数学家费马通过推广毕达哥拉斯方程x2+y2=z2，提出了举世闻名的费马猜想：“xn+yn=zn(n≥3)是否有整数解”.虽然推广的重要作用得到了数学研究者们的普遍认同，但从数学教学实践来看，一些教师并未充分认识数学推广的教育价值.因此，下文在厘清数学推广概念、特征的基础上，分析数学推广所具有的教育价值.

1 数学推广的概念界定

什么是数学推广呢？张景中院士认为：“数学中的推广就是扩大命题条件中有关对象的范围，或扩大结论的范围，即从一个事物的研究过渡到包含这一事物的研究”[1]；罗增儒教授指出：“数学推广是这样一种研究方法，从一个对象过渡到考虑包含该对象的一个集合，或从一个较小集合过渡到考虑包含该集合的更大集合”[3]；郑隆炘教授将数学推广定义为“在一定范围内或一定层次上对数学概念、定理、法则进行拓展，使之在更大范围或更高层次上成立，此外，也指对条件、结论进行结构分析以后，进行适当变化，使得到的新命题为真”[4]；汪纯中教授认为：“把一个数学命题中的某些特殊的条件一般化(比如取消某些条件过强的限制)，从而得到更普通的结论，叫做数学命题的推广”.[5]尽管上述数学推广的概念表述不同，但都强调了对象范围变大，都体现了研究过程.当然，差异也较为明显：一些界定要求推广后的命题为真，一些界定对此未做要求.是否一定要求推广后得到的命题为真呢？我们认为推广后命题的真假性可不作要求，比如，前文所述的费马猜想是毕达哥拉斯方程的推广，但推广提出358年后才被数学家安德鲁·怀尔斯所证明.此外，一些定义侧重于问题结构上推广，而忽视从问题解决方法上推广.基于此，我们把握推广的“抓手”(问题结构或问题解决方法)和本质(研究过程)，重新界定数学推广的概念：数学推广是指根据问题结构或解决方法，将数学问题从一个较小的范围拓展到更大范围的研究过程.

2 数学推广的特征分析

2.1 问题性

数学推广的过程是问题伴随的过程.首先，问题是推广的生长点，推广必须基于数学问题展开，正所谓“没有问题，何来推广”；其次，问题是推广的驱动点，推广实质上是原问题作为初始问题触发新问题产生的反复、螺旋上升的过程，问题驱动着推广活动的开展和深化；最后，问题是推广的落脚点，推广目的是在更大范围上生成新问题，且推广的最终成果以问题呈现.

2.2 系统性

数学推广的过程是不断完善问题系统的过程.钱学森认为：“系统是由相互作用相互依赖的若干组成部分结合而成的，具有特定功能的有机整体.”推广通过对问题或方法的一般化，形成一个由初始问题生成的意义系统，揭示更为深刻、更为普遍的数学事实或规律，构成一个结构前后一致、逻辑连贯的问题域.特别指出，问题域中初始问题是整个系统的基石，在结构或方法上支撑新问题，而推广得到的最一般问题处于系统的顶层，统摄整个问题系统.

2.3 研究性

数学推广的过程是研究的过程.数学推广不仅仅是数量上的简单增加或呈现形式的简单变化，通常是一个探索与发现、猜想与论证的过程.[3]这一过程涉及问题提出与问题解决方法的寻求，往往会经历观察、归纳、类比、联想、猜测、论证、反思等思维活动.由此，数学家们一致认为“数学推广本身就是数学研究的重要方法.” 比如，米山国藏就曾指出：“每当我发现一个新定理，就立即集中力量从各方面考查这个定理能不能将它一般化、能不能推广，从而一步一步进行研究工作.”[6]

2.4 创新性

数学推广的过程是创新的过程.数学推广不是简单模仿、机械重复，它是一项富有创造性[7]、伴随生命活力的数学活动，其实质就是创新与发现.[3]通过推广产生新问题，发现新方法，促使新系统的构建，推动该问题领域知识和研究方法的不断完善.

3 数学推广的教育价值

当教育指向核心素养，“知识核心时代”将真正走向“核心素养时代”.在关注人的素养发展，推进人的素养发展与时代发展需求相融合的进程中，“怎样培养人”比“培养怎样的人”更重要，“怎么教”“怎么学”比“教什么”“学什么”更重要.[8]这正如毕达哥拉斯所说，在数学的天地里，重要的不是我们知道了什么，而是我们怎么知道什么.数学推广引领学生超越浅层的知识学习，进入知识内在的逻辑领域，挖掘知识内涵的丰富价值[9]，体会数学研究的重要意义，它不仅是一种重要的数学研究手段，也是一种重要的数学学习活动，具有丰富的教育价值，是发展学生数学核心素养的重要载体.

3.1 培养问题意识

《普通高中数学课程标准(2017年版)》(下文简称《课标2017》)指出：通过高中课程的学习，进一步培养学生“四能”，即发现问题、提出问题、分析问题和解决问题的能力.[10]其中，提出问题能力尤为重要.这是因为问题是思维的起点和动力，提出问题往往比解决问题更具创造的成分.正如大数学家希尔伯特所说：“从数学发展的历史来看，数学问题的大量提出是数学充满生命力的体现.”认识论研究专家安德烈·焦尔博士在研究有意义的学习活动时，强调“发问”是衡量学习是否发生的一个重要标准.由此可见，提出问题对激活数学生命力，构建有意义学习具有重要地位.那如何才能提出问题呢？研究表明，问题意识是问题提出的直接基础[11],强烈的问题意识有助于学生更好、更快地跨越最近发展区，驱动学生主动去发现问题、提出问题.[12]具体到数学学科，数学问题意识驱动学生自觉主动地对已有数学问题进行再提问和反思，并形成一种探索创新的心理品质.[13]数学推广在将问题从“小范围”到“大范围”变化拓展的过程中，在将方法从“原问题”到“新问题”应用创新的过程中，始终将学生置身于问题情境，引导学生不断思考如何提问，如何答问，如何再提问，这为问题意识的培养提供了现实土壤和可靠原动力.

3.2 完善认知结构

(1)完善知识结构

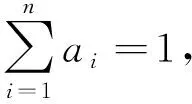
(2)丰富认知模式

莱考夫认为：“认知模式是人与外部世界互动的基础上形成的认知方式.”通俗地讲，认知模式指学习者对信息的获取、处理的方式.在(*)的推广中，涉及多种认知模式：由2元命题、3元命题、4元命题的研究上升到n元命题，既体现了“假设—证伪(真)—修正”的研究方法，又渗透了“特殊到一般”的思维方式；由已有2元命题不直接跳步到n元命题研究，而是先对3元、4元等简单情形研究，既体现了类比、归纳推理的基本范式，又展现了“以退为进”的思维策略；从单一问题(元变化)上升到关联问题(次数变化)，再到问题系统(元和次都变)，既体现了“变与不变”的认知方式，又刻画了灵活变通的思维品质.由此可见，推广活动极大地丰富、发展了学习者的认知模式.

3.3 体验研究历程

《课标2017》将数学建模活动与数学探究活动作为四条主线之一，贯穿于必修、选择性必修和选修课程之中，并且专门在必修课程中设置了6个学时加以实施.[10]由此可见，开展数学探究活动引导学生了解研究的基本方法、经历研究的历程是当前数学课程的重要要求和改革方向.如何有效地开展探究活动呢？数学推广恰好为学生提供了探究的基本方法和路径，这是因为数学推广本身就是数学研究的重要方法，数学问题推广的过程本身就是数学研究的过程.具体来讲，学生运用数学思维方法将问题变化拓展，获得新结论或新问题的同时，体验数学研究的一般步骤：确定选题——拟定计划——收集资料——深入分析——得出结论——撰写报告(或论文).同时，在对问题推广的过程中，学生体会着三对相互依存的辩证关系：“特殊”和“一般”：特殊性包含于普遍性，普遍性寓于特殊性；“猜想”与“论证”：要有大胆猜想的求知勇气，也要具备小心求证的求真精神；“乐趣”和“枯燥”：变枯燥的学习为幸福的研究，塑实事求是和勇于创新的科研品质.

3.4 增强创新能力

随着信息革命的到来，传统的知识教育模式已不能满足社会发展的需求，给学生提供适应未来发展的核心能力才是现代教育的目标和归宿.当今社会的竞争，与其说是人才的竞争，不如说是人的创新能力的竞争，对学生创新意识和创新能力的培养已成为全球教育界所关注的共同话题.对数学推广而言，从强调问题意识到经历研究过程，其实质就是重视创新，重视学生创新意识和创新能力的培养，这是基于时代发展要求下的数学教育的魂.[16]数学推广活动引领学生大胆猜想，勇于尝试，用已有的数学知识和方法解决问题，并在问题推广中，积累数学活动经验，形成数学探究能力，为增强创新能力提供丰富“营养”.