使民以时

王小静

摘要：孔子曰：“道千乘之国，敬事而信，节用而爱人，使民以时。”孔子是站在君主治理天下的立场，从物质时间的节约角度提出要求。“十年树木百年树人”有些事情或许可以得过且过，但教学不能敷衍塞责，来不得半点马虎。作为教师，我们应站在育人、教学的立场，从时间成本的角度去要求自己提高教学质量，打造“阳光高效课堂”。

关键词：阳光高效课堂；学案；自主探索；变式与发散

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2021）09-0071

在“减负提质”的教育理念下，我校提出了“阳光高效课堂”，为我们九年级复习课堂指明了方向，在九年级复习课中如何取得高效？这些问题困惑着笔者，一节课的时间极为有限，在有限的时间里将整章知识点逐一讲到，是不现实也是不科学的。“使民以时”给笔者很大的启发，真正领悟“阳光高效课堂”中的高效，把握时间、教学以时，提高教学效率。

一、教学相长

只有思考的教师才能引导学生思考，而思考着的学生反之亦能促使教师思考，如果教师没有这个意识，那么“取法乎下”，学生只能“仅得下下”，谈何效果。所以，教师要做到“学生未思我先想”“我与学生共成长”。在教学中，笔者搭建知识体系，串联学科网络通过“联”性问题的出示，使学生在短时间内有效地建构数学知识网络，在整理复习中进而掌握了知识的应用。例如，我们在复习矩形性质这节课时要掌握并运用矩形的以下知识：矩形的四个角都是直角；对角线互相平分且相等；对角线把矩形分成两对全等的直角三角形；矩形是轴对称图形；矩形的面积等于两邻边的乘积。

问题出示：如图，矩形ABCD的两条对角线相交于点O，

（1）找找图形中有哪些特殊的三角形。

（2）要添加什么条件时，能使△AOB更特殊呢？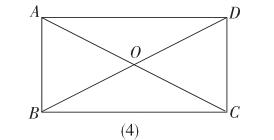

（3）在（2）的基础上，能不能求出对角线的长度？若不能，那要增加什么条件呢？若AB=4cm，矩形ABCD的对角线是多少？

（4）过点D作DE∥AC，交BC的延长线于E，这时，∠DBE与∠DEB有什么特殊的关系？

“联”在问题上，有时我们也“联”在图形上，笔者在课堂上也是经常设计。时常总结巩固，学会触类旁通。“学而时习之”学习了时时练习，时常进行整理和复习，获得知识和智慧。我们在讲述一个问题后，若能及时总结和巩固练习，才会达到触类旁通的效果，进行思维。

二、多算胜少算不胜

多算胜，少算不胜，古代一种作战思想。语源于《孙子·计篇》：“夫未战而庙算胜者，得算多也，未战而庙算不胜者，得算少也。多算胜，少算不胜，而况于无算乎！吾以此观之，胜负见矣。”意为作战前计算周密，胜利条件多，可能胜敌；计算不周，胜利条件少，就不能胜敌。深化变式练习，笔者有时要一题多讲和变式练习，来引导学生寻找解决问题策略的多样化及优化，促使学生的思维得到发散和升华。在一题多讲中，学生可以从不同的角度分析、解决问题，促使学生根据自己的认知基础和思维特点进行选择，发现具有个性差异的解题方法，从而使每一个学生探索出解决问题的有效方法。展现不同解法，发散学生的思维，发展学生的数学思维能力。变式练习是为了把问题讲透、思路展开揭示本质，促使学生的分析能力得到提高、認识得到深化。试题变式促进学生对知识点本质的掌握，在对知识进行系统梳理，形成知识网络的同时对典型问题进行变式训练，达到举一反三、触类旁通的目的。

三、好为人师授人以渔

孟子说：“人之患在于好为人师。”总以为自己知道的，不遗余力地去教给学生，生怕学生自己弄不明白。可是教不是万能的。陶行知先生告诉我们：教是为了不教。教学生知识，不如让学生学会怎么学，所谓“授人以鱼，不如授人以渔”。九年级的学生有独立思考和探索知识的能力，并能通过阅读课本，结合自己的理解逐渐完善自己的想法，把所学内容整理成有纲有目的内容体系，抓住思想方法的脉络，把书本看“薄”，从而发现知识之间的联系，学会知识之间的转化，做到心中有数、触类旁通，促进知识技能的形成。此外，教师还要善用网络，事半功倍。利用钉钉上的学习功能上传一些资料和视频供学生学习，让学生及时完成，并及时反馈学生的做题情况。这样，在备课时可以更有针对性，对上课的教学内容更有指向性，从而收获更好的效果。

四、三省吾身

仅仅停留在做题与改错题的层面上，那么所谓使得内化、能力的培养与智慧的提升便成为一句空话。针对不同层次的学生，教师可以引导学生做好复习反思。在复习中有一种简单而又高效的方法，那就是编写错集。让我们把有限的、宝贵的时间全都花在自己最该花时间的地方，以保证自己有限的精力真正做到“好钢用在刀刃上”，同时也避免了复习时的单调与乏味。编写的目的是诱导学生暴露他们原有的思维方法和过程，利用它来反思自己学习中存在的问题，寻找错误产生的原因。通过反思，可以加深对知识的掌握、提高数学的思维能力，调动其学习的积极性，培养学生的思维能力，保证每一个字、每一个步骤都不能出错，不能再犯类似的错误，给学生对待学习、对待成长以深刻的启迪。另外，教师提供一些资料、开放性的问题来引导学生围绕一定的主题，根据自身能力选一些“跳一跳可以摘得到”的题目自行练习，让学生感悟数学思想方法，体会探究实际上并不神秘，也并非高不可攀。同时，教师还要进行自主探索，使学生在探索的过程中进一步理解所学知识，让学生经历多角度认识问题、多种形式表现问题、多种策略思考问题、尝试解释不同解答的合理性，以发展其创新意识和实践能力。在完成的过程中，学生运用所学知识提出问题、解决问题，对学生的解题能力和方法也有了质的飞跃。

笔者不敢奢望在教育事业的大课堂中能“得其志”“得其人”，仅“得其曲”“得其数”的笔者明白论语中的“虽曰未学，吾必谓之学矣”，也就是说真正的学习者、研究者首先是行动者。在已“得其志”的教师的指引下，路是正确的，教育的前方是光明的，我们只有行动起来，以勤补拙，才会有所进步、有所领悟，争取做到“使民以时”为学生打造“阳光高效课堂”。

参考文献：

[1]胡爱民.用《论语》思想提升数学教育智慧[M].重庆：西南师范大学出版社，2010.

（作者单位：浙江省温州市第二十中学325011）