鉴别性非负表示分类及其在人脸识别中的应用

徐然然，吴小俊，尹贺峰

江南大学 物联网工程学院，江苏 无锡214122

近年来，随着各种社交软件的迅速普及以及网络速度的快速提升，在线分享的照片越来越多。如何对这些图像数据进行分类识别，成为图像处理领域中的研究热点。图像像素的增加，使得通过图像生成的空间维数成倍增加，容易导致维数灾难。为了解决维数灾难问题，通常对图像进行特征提取。在特征提取阶段，将图像转换成特征空间中的低维向量，经典的基于子空间学习的人脸识别方法有主成分分析（Principal Component Analysis，PCA）[1-2]、线性判别分析（Linear Discriminant Analysis，LDA）[3-6]等方法。

近年来，稀疏表示在很多领域得到广泛的研究和应用。Wright 等[7]首先提出了稀疏表示分类算法（Sparse Representation based Classification，SRC）用于人脸识别，将训练样本组成一个过完备的字典，使用这个字典对测试样本稀疏线性表示，然后计算相应的重构误差，将测试样本划分在最小重构误差对应的类别中。SRC使用L1 范数对表示向量进行稀疏约束，但当SRC 中样本过多时，训练样本生成的字典规模增大，导致后续样本的稀疏分解过程变慢。

针对这个问题，Zhang 等人[8]提出了协同表示分类算法（Collaborative Representation based Classification，CRC），CRC强调了协同机制在模式分类中的作用，利用L2 范数对表示向量进行有限的稀疏约束，由于引入L2范数，CRC可以得到闭式解。实验证明，CRC能取得和SRC 相当的识别性能，同时计算复杂度明显低于SRC。另外，Cai等人[9]从概率的角度解释了协同表示机制，并且提出了概率协同表示分类算法（Probabilistic CRC，ProCRC），CRC 可以看作是ProCRC 的一种特殊形式。受稀疏表示在不同领域成功应用的启发，Yin 等人[10]提出一种基于局部二值模式和稀疏表示的特征融合方法，在该方法中特征以串行方式进行融合。为了处理训练和测试样本都受到污损的情形，Yin 等人[11]提出一种低秩矩阵恢复算法，该方法通过低秩投影矩阵可以对污损的测试样本进行恢复。Chen 等人[12]将稀疏表示与基于核范数的误差矩阵回归相结合，可以有效地将样本中的连续遮挡移除。

考虑到不同类别之间的鉴别信息，Xu 等人[13]提出了鉴别稀疏表示分类算法（Discriminative Sparse Representation based classification，DSR），由于引入了去相关性正则项，使得图像分类的性能得到提升，同时DSR能得到解析解，可降低计算复杂度。

无论是SRC、CRC还是他们的拓展算法[14-15]，都无法避免编码系数中的负数表示。受非负矩阵分解（Nonnegative Matrix Factorization，NMF）[16]的启发，Xu 等人[17]提出了非负表示分类器（Non-negative Representation based Classification，NRC），NRC 去掉不利于分类的信息，提高同类样本的贡献比重，同时限制异类样本贡献比重。

虽然NRC 取得了优异的识别效果，但是NRC 没有考虑到样本之间的相关性，本文提出的方法在NRC 的基础上添加鉴别项，减少相似样本类别之间的相关性。

为了说明本文方法Discriminative Non-negative Representation based Classification（DNRC）正则项的有效性，下面给出一个例子，从Extended Yale B[18]数据集中取一个测试样本y，该样本的真实类别是第13类，对比DNRC 和NRC 算法在Extended Yale B 数据集上的编码系数。

图1（a）是用DNRC 算法得到的测试样本的编码系数，图1（b）是用NRC 算法得到的测试样本的编码系数，图1（a）和（b）中红色标记是真实类别所对应的编码系数，图1（b）中绿色区域是NRC 错误分类对应的编码系数。

图1 分别用DNRC和NRC算法计算的编码系数

用柱状图表示出测试样本y在训练字典上对应的残差，该测试样本的真实类别是第13 类，由图2（a）看出，DNRC计算出来的最小残差属于第13类，因此DNRC正确地将该测试样本分类，由图2（b）看出，用NRC计算出来的最小残差对应第7类，与测试样本的真实类别不符。其中，DNRC 算法的最小残差比为1∶1.09，NRC 算法的最小残差比接近1∶1。

图2 分别用DNRC和NRC算法计算的残差

由此看来，虽然NRC 的最大编码系数位于正确的类别，但是最大编码系数得到的残差并不是最小的，导致测试样本误分，但是本文方法在NRC 的基础上添加去相关正则项，能够有效地减少错误分类情况，提升识别率。在4 个公开数据集上的实验表明本文方法有着突出的表现。

1 相关工作

1.1 稀疏表示分类器

假设训练集一共有L类样本，用Xi表示第i类样本集，训练样本集可以表示为X=X1,X2,…,XL，其中第i类共有m个样本，每个样本排列成一个列向量，表示为Xi=[xi,1,xi,2,…,xi,m]，维数为d，总样本的个数是n(n=m×L)。对于一个测试样本y∈Rd，寻找一个稀疏系数c∈Rn，使与y不同类别样本对应的系数较小，趋近于0。构建模型y=Xc∈Rd，使得编码系数c稀疏。SRC的目标函数如下：

其中，λ>0 是平衡参数。求解L1 范数优化问题有很多方法，通过L1 正则化最小二乘法[19]，快速迭代收缩[20]和阈值算法[21]，同伦算法[22]等算法均可求解得到稀疏编码系数，计算最小重构误差r，第k类重构误差如下所示：

其中ck(k=1,2,…,L)为第k类样本对应的编码系数，测试样本的类别为最小重构误差所对应的类别，如下所示：

1.2 非负表示分类器

SRC在图像分类问题上有广泛的应用和研究，虽然SRC 在识别性能上表现优异，但是SRC 以及SRC 的拓展算法都没有考虑到系数编码中负数对识别的影响。NRC 表明，编码系数中的负元素来自训练样本中与测试样本不同类别的样本，对样本正确的分类有不利的影响。受非负矩阵分解的启发，NRC 对编码系数进行非负约束，构建如下模型：

通过交替方向乘子法[23]对式（4）迭代优化，引入辅助变量z，得到如下等价形式：

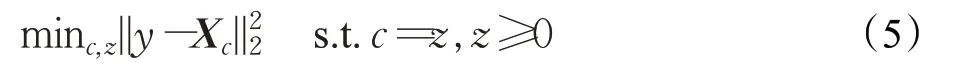
构建拉格朗日函数如下：

其中，δ是拉格朗日乘子，μ是惩罚参数，依次对参数进行迭代求解，具体算法过程可以参考算法1。

1.3 鉴别性稀疏表示分类器

DSR通过引入去相关正则项，使不同的类别更具区分性，有助于表示分类方法获得有鉴别性的类别残差，更好地识别测试样本。

DSR的目标函数如下：

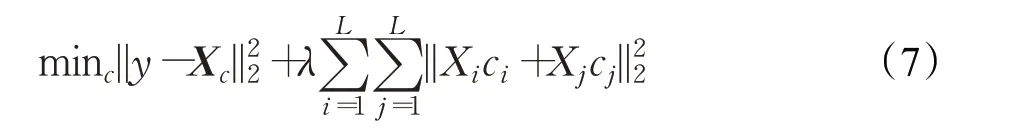
经过推导可以得到编码系数c的解析解。具体算法流程如算法2所示。

2 本文方法

2.1 算法模型

本文提出的基于鉴别性非负表示的人脸识别算法（DNRC），主要在非负表示的基础上添加鉴别性信息。第一步，采用了基于非负表示的分类器，NRC的研究表明同类的训练样本对于重构表示的贡献是正的数值，异类的训练样本对于重构表示的贡献是负的数值，非负表示约束可以减少其他类别对测试样本重构表示的影响；第二步，添加正则项，减少类别之间的相关性。本文方法使用的是L2 范数，不是L1 范数或者L2，1 范数，通过推导能够得到闭式解，比SRC的运行速度快。

本文算法的模型如下：

第i类训练样本对应的表示系数用ci表示，测试样本的估计向量就可以写成Xici，本文方法加入鉴别信息项将该项展开来看，可以写成由此看来，为了最小化该正则项，等价于同时最小化其中i,j={1,2,…,L}。

引入辅助变量z，式（8）可以写成如下的等价形式：

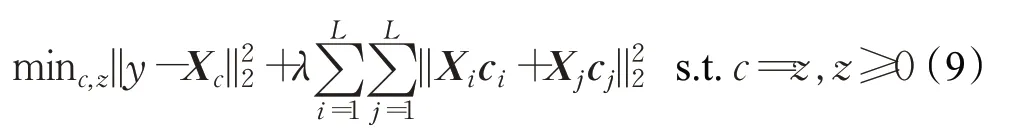
其中，λ>0 为平衡因子，平衡式（9）中的各项大小。本文利用交替方向乘子法来对式（9）进行优化求解，具体过程在下一节中详细介绍。

2.2 模型优化

将式（9）转换成拉格朗日函数，利用交替方向乘子法进行推导优化。构建拉格朗日函数如下式所示：

首先，对式（10）的第一项求偏导，结果如下所示：

然后，对式（10）的第二、三项合并求偏导，结果下式所示：

接着，将式（10）的最后一项用f表示，即：

对式（10）的最后一项关于c求偏导，结果如下所示：

经过化简求导，整理得到各个变量的迭代形式：

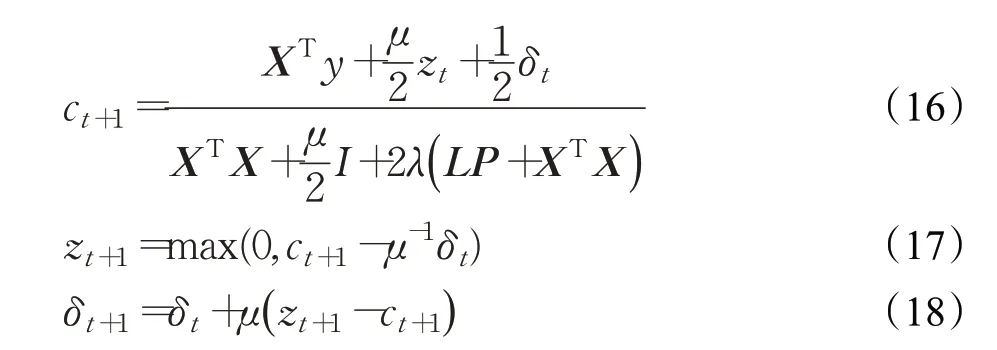
由于λ(LP+XTX)与系数编码无关，可以事先计算，以便减少计算复杂度。通过将式（16）、（17）、（18）交替更新，重复进行，直到达到收敛条件，或者达到最大迭代次数。算法的收敛条件：当设定的误差tolerance>0是一个足够小的值时，同时满足条件还有

具体算法流程如算法3所示。

通过交叉验证法得到最优参数λ，利用算法3得到测试样本y的表示系数，接着利用编码系数计算重构误差，对测试样本y进行分类，本文算法流程如算法4所示。

3 实验及结果分析

为了验证本文算法的有效性，分别在AR[24]、GT[25]、Extended Yale B 和LFW[26]这4 个公开数据集上进行实验。在实验中，通过与其他分类识别算法SRC、CRC、ProCRC、LRC、DSR、NRC进行对比，比较人脸识别正确率以及运行时间。在GT 数据集上研究不同维数，以及不同训练样本个数对识别率的影响。

3.1 各个数据集上的实验结果

AR数据集。采集了126名人员（其中男性70名，女性56 名）的彩色正面照片，对于每一个实验人员的图像，采集条件不同，包含光照差别、表情变化，以及是否有遮挡。本文实验取AR数据集的子集，包括50名男性和50名女性的图像，每个实验对象有14张图像，取其中7 张作为训练样本，另外7 张作为测试样本。每张图像缩放为60×43大小，通过PCA降维到600维。

GT数据集。Georgia Tech数据集采集了50名人员的彩色正面照片，每一个实验对象有15张图像，分别在不同姿态、表情、光照以及背景的情况下拍摄。整体像素为680×480 像素，其中人脸的平均大小为150×150 像素。经过裁剪之后是正面和稍有倾斜的人脸数据集，部分示例图像如图3（b）所示。实验中对每个实验对象随机取8 张图像作为训练样本，剩下的7 张作为测试样本。重复10 次实验取识别率的平均值，每张图像缩放为125×125大小，通过PCA降维到700维。

图3 4个数据集的部分示例图像

Extended Yale B数据集。Extended Yale B数据集采集了38 名人员的2 414 张正面彩色图像。每一个实验对象最多有64 张图像，最少有59 张图像。裁剪后的平均像素是192×168像素，实验环境严格控制不同的光照条件，部分示例图像如图3（c）所示。实验中将图像降采样为54×48像素通过PCA将维数降到540维。

LFW数据集取8张人脸图片作为训练样本，剩下的作为测试样本，实验结果取10 次实验的平均识别率。包含了非限制环境下的人脸图像。一共有1 680名人员的13 000多张人脸图像。本文实验使用LFW数据集的子集，使用86 名人员的1 251 张人脸图片，每个实验人员最少有10张人脸图片，最多有20张人脸图片，因此实验中对每个实验人员随机选平均值。将每张图像缩放为32×32大小。

表1 给出各种对比算法在4 个数据集上的识别率，本文算法在AR、GT、Extended Yale B、LFW上的参数λ取值分别为0.000 01、0.001、0.000 1、0.000 01 时取得最优实验结果。

表1 各算法在4个数据集上的识别率%

从表1 看出，在4 个数据集上，本文提出算法的识别率要优于其他方法。在AR 数据集上，本文方法比DSR 高出6.15%，比NRC 高出0.43%，显然，在AR 数据集上，本文算法比其他算法有优势。在GT 数据集上，本文提出方法比SRC 高2.46%，比DSR 高出5.89%，比NRC 高出3.38%，并且高于其他对比算法。在Extended Yale B 数据集上的实验结果显示，本文提出方法比DSR 的识别率高出2.15%，比NRC 高出0.82%。LFW 数据集中的图片是在非限制条件下收集的，识别比较困难，各种方法在LFW 数据集上的识别率都不是很高。但是本文提出方法的表现突出，比CRC 的识别结果提高了17.94%，比DSR 高出了6.93%，比NRC 高出0.48%。

3.2 运行时间对比

算法的测试时间主要来自计算训练样本对应的重构误差，由于不同的算法的编码系数的计算方式不同，所以在运行时间上的差异很大。为了验证本文算法效率，表2 列出了在AR、GT、Extended Yale B、LFW 这4个数据集上的总的测试时间。

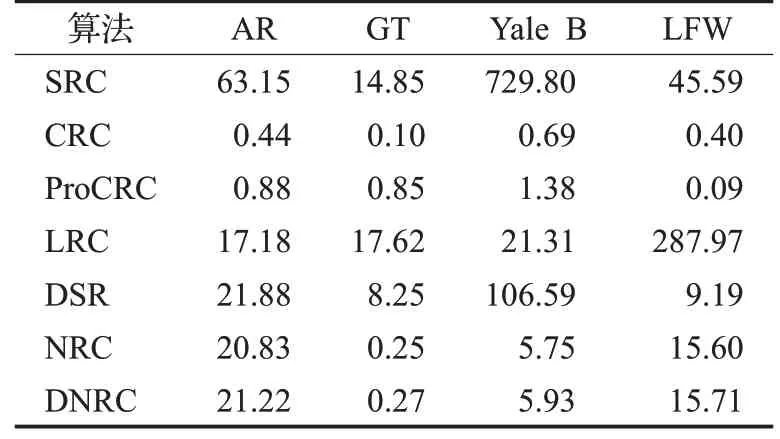
表2 不同算法的测试时间对比 s

由表2可知，不同方法的测试时间与数据集的大小有关系，GT 数据集的测试时间相比其他数据集短。相同数据集下，不同识别方法的测试时间也有很大的区别。由于SRC 使用的是L1 范数计算，虽然在有些数据集上的识别结果比其他方法优异，但是SRC需要迭代优化。CRC和ProCRC可以得到解析解，大大降低测试时间，在4 个数据集上的测试时间显示，本文算法在测试时间上很有优势。本文提出方法的测试时间比CRC多，但是相比SRC有了很大的提升。

3.3 不同维度图像对实验结果的影响

实验中训练样本通过PCA降维的维数对实验结果有一定影响，为此在GT 数据集上进行实验。将样本分别投影到到54、84、120、150、200一共5种维度的子空间中，不同维数下的识别结果如表3所示。

表3中的λ是正则项参数的取值，其中识别率最高的数值用黑体表示。为了更加直观地研究不同维数对于实验结果的影响，用折线图表示识别率如图4 所示。从图4 可以看出，当λ取0.1 时，在5 种维数上的识别率都比其他λ取值识别率高，当PCA 的维数增加时，识别率随之增加，但是当维数增大到150时就没有很大的提升，降维过低时会损失信息，对识别结果不利。当维数过大时，对于识别结果没有太大的影响，反而增加计算时间。

图4 在GT数据集上不同维数下的识别率

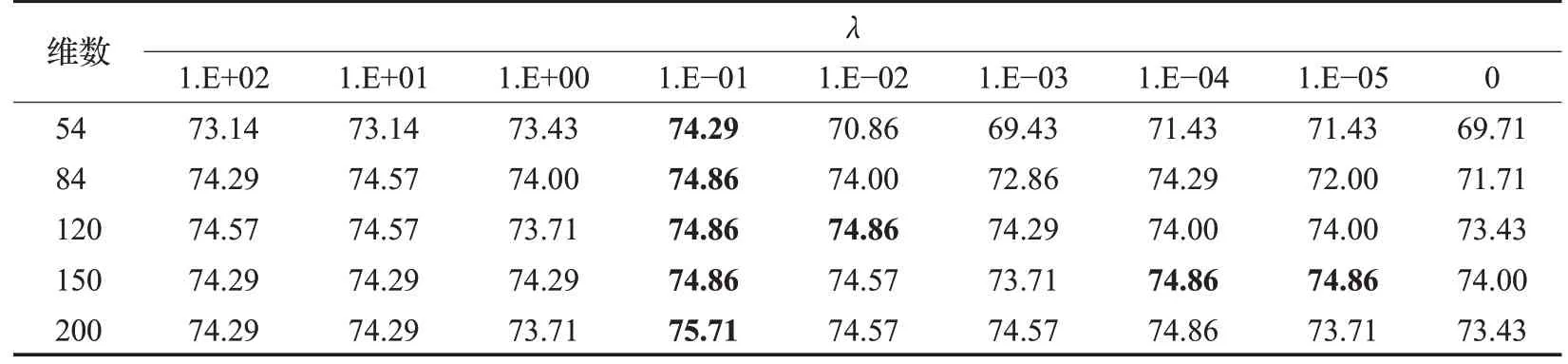
表3 不同维度下本文算法的识别率 %

3.4 不同训练样本数对实验结果的影响

数据集中训练样本的个数对实验结果有很大的影响，为了研究不同训练样本数对实验的影响，在GT数据集上控制不同的训练样本个数，随机选择N（N=2，4，6，8，10，12）幅图像作为训练样本，重复10 次实验取实验结果的平均值，实验结果如表4 所示，λ作为平衡参数，识别率最好的用黑体表示。

表4 不同样本数时本文算法的识别率 %

当训练样本数不同时，实验结果最好时参数λ的取值并不相同，取值变化比较大。

在GT 数据集中，随着训练样本数增加，识别率升高，从图5直观地看出，在所有λ的取值上，训练样本数为2 时，识别率很低，当训练样本增加时，识别率随之增加。

图5 在GT数据集上不同训练样本数的识别率

4 结束语

本文提出一种基于鉴别性非负表示的分类算法，利用交替方向乘子法对提出的模型进行优化。在4 个公开数据集上都取得了较好的识别效果，说明本文算法的优越性。本文算法使用的是传统特征，近年来深度学习在各个领域取得了优异的性能，今后可在深度特征上验证本文算法的性能。此外，本文使用的训练样本是干净的（没有遮挡和像素破坏），为了处理实际应用中的图像，可以考虑利用低秩矩阵恢复算法对样本进行处理，进一步提高算法的识别率。