一类Sylvester矩阵方程异类约束解的迭代算法

2021-07-14段复建

重庆理工大学学报(自然科学) 2021年6期

段复建，原腾

（桂林电子科技大学数学与计算科学学院，广西桂林 541004）

Sylvester矩阵方程在控制理论、切换系统、扰动分析等［1－4］众多领域有着广泛的应用。近年来，很多学者对这类方程进行了研究，并取得了一些成果。如Wang等［5－8］研究了求线性矩阵方程一般解的迭代算法；彭卓华等［9－10］分别研究了求线性矩阵方程的中心对称解、自反最佳逼近解的迭代算法；徐玉霞等［11］运用广义奇异值分解和投影定理，研究了线性矩阵方程的对称M对称最佳逼近解。目前为止，对于Sylvester矩阵方程的异类约束解的研究相对较少。本文针对求解矩阵方程A1X1B1＋A2X2B2＋＝F的自反和双对称约束解问题，将方程等价转化，使其转化为具有自反和双对称约束的正规矩阵方程组，从而构建求其约束解的自适应共轭梯度算法。

用Rm×n表示m×n的实矩阵的集合，A⊗B表示矩阵A与B的Kronecker积，R（A）和（A）分别表示矩阵A的列空间和将矩阵A按行拉直构成的列向量。定义同阶矩阵A与B的内积〈A，B〉＝tr（ATB），由此导出的矩阵的F范数为‖A‖＝。设P1，P2∈Rn×n是对称正交矩阵，若X∈Rn×n满足P1XP2＝X，则称X为关于矩阵P1，P2的广义自反矩阵。特别地，当P1＝P2＝P时，相应的广义自反矩阵就是通常的自反矩阵，记关于矩阵P的自反矩阵的集合为。用ei表示单位矩阵的第i列，记S＝（en，en－1，…，e1），则有S2＝In，ST＝S，若X∈Rn×n满足X＝XT＝SXS，则称X为双对称矩阵，记n阶双对称矩阵集合为BSRn×n。当，X2∈BSRn×n时，称之为自反和双对称约束矩阵。

考虑Sylvester矩阵方程的以下2个问题，建立求式（1）所表示的方程的自反和双对称约束最小二乘解的自适应共轭梯度算法，并在约束解集中找到给定矩阵的最佳逼近矩阵。

问题1 设Ai，Ci∈Rm×n，Bi，Di∈Rn×l，F∈Rm×l，求，X2∈BSRn×n，使得

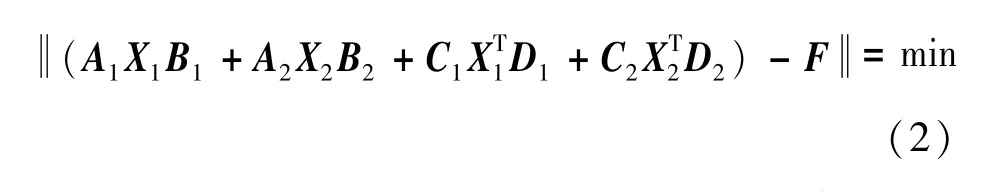
问题2用SE表示问题1的解的集合，给定X0∈Rn×n，在SE中求，使得

当式（1）所表示的方程有自反和双对称约束解时，称式（1）是相容的，此时直接用共轭梯度算法求解式（1）的自反和双对称约束解；当式（1）没有自反和双对称约束解时，称式（1）是不相容的，此时不能直接对式（1）进行求解，通过构造等价转化，将不相容的方程的自反和双对称约束解问题转化为相容的方程组的约束解问题，此时即可求出式（1）的自反和双对称约束最小二乘解。为求解不相容情况下式（1）的约束最小二乘解，下面对问题1做等价转化。

1 问题1的等价转化

当式（1）所表示的方程不相容时，对它作等价转化，将其转化为具有自反和双对称约束的正规矩阵方程组。因此引入以下记号

g（X1，X2）与Q分别表示式（1）等价转化为正规方程组的左端与右端，即转化后的正规方程组可以表示为g（X1，X2）＝Q。

定理1求解问题1等价于求矩阵方程组

的自反和双对称约束解，且矩阵方程组（3）必有自反和双对称约束解。

证明当（P），X2∈BSRn×n时，有X1＝PX1P，＝SX2S。因此，求解X1∈，X2∈BSRn×n满足式（2）等价于求解X1，X2∈BSRn×n使得

下证求极小值问题（4）的解等价于求方程组（3）的自反和双对称约束解。约定矩阵的乘积运算优先于矩阵的Kroncker积运算。引进记号xi＝。为简单起见，记

其中Tm，n表示满足的列交换矩阵。

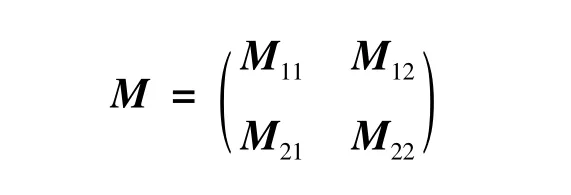
令考虑线性矩阵方程组

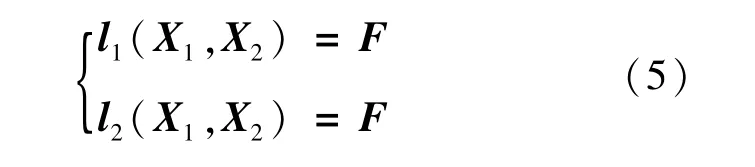
可得求解极小值问题（4）的解等价于求解方程组（5）的最小二乘解。将式（5）按行拉直可得线性方程组Mx＝v，它的正规矩阵方程组为MTMx＝MTv，写成矩阵形式即方程组（3）。因此求解问题1等价于求解方程组（3）的自反和双对称约束解。

再证方程组（3）有自反和双对称约束解。因为正规方程组MTMx＝MTv有解，所以矩阵方程组（3）有解。设为矩阵方程组（3）的一般解，则有＝Q。

2 求解问题1的自适应共轭梯度算法

参考文献［12－15］中算法的基本原理，建立求解矩阵式（1）的自适应共轭梯度算法。在矩阵方程相容情况下进入外迭代算法，不相容情况下进入内迭代算法（步骤4～7）。下面建立求解式（1）的自反和双对称约束最小二乘解的自适应共轭梯度算法。

步骤1 给定初始矩阵∈BSRn×n，置k1，计算

步骤2 若Rk＝O，停止；否则继续；

步骤3 若Zk≠O，转步骤8；否则转步骤4；

步骤4 取∈BSRn×n，置，计算

步骤5若＝O，停止；否则，计算

步骤6计算

步骤7置，转步骤5；

步骤8计算

步骤9计算

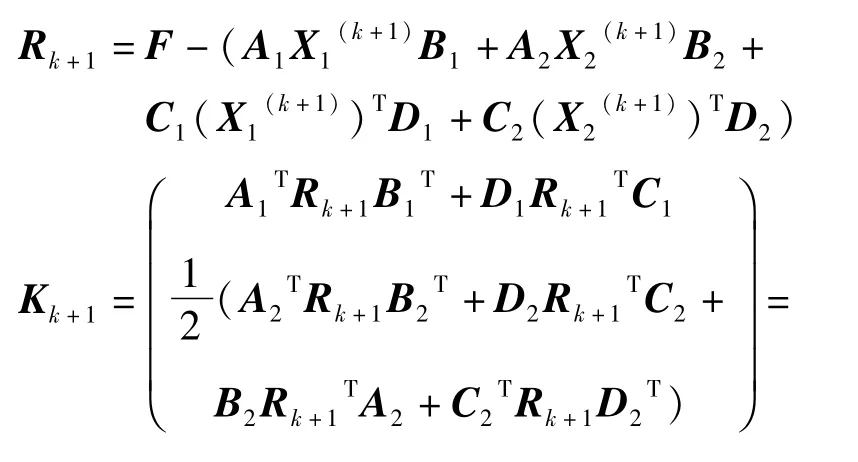
步骤10置，转步骤2。

注在求解式（1）的自反和双对称约束最小二乘解时，步骤4中的是算法在外迭代中断时得到的矩阵，作为内迭代的初始矩阵。

性质1若是式（1）的自反和双对称约束解，对于任意选取的初始矩阵算法中的矩阵X（i），Ri，Zi（i＝1，2，…）满足〈Zi，X*－X（i）〉＝

性质2若是问题1的解，即式（1）的自反和双对称约束最小二乘解，则对于算法外迭代中断时得到的矩阵作为内迭代的初始矩阵，Y2∈BSRn×n，算法中的矩阵Y（i）（i＝1，2，…）满足

性质3对于算法中的Ri，Zi，有

性质1～3的证明可参考文献［14－15］。

定理2对任意选取的初始矩阵算法可在有限步计算后求得问题1的一组自反和双对称约束最小二乘解。

证明当矩阵方程相容时，若存在k≤n2使得Rk＝O，则是问题1的一组解；否则算法继续进行，得到Rn2＋1，由矩阵基的性质和性质3可得R1，R2，…，Rn2构成有限维矩阵空间Rn×n的一组基且〈Rk，Rn2＋1〉＝0（k＝1，2，…，n2），因此Rn2＋1＝O，即，是问题1的一组解，也就是式（1）的一组自反和双对称约束解。

综上，无论矩阵方程是否相容，问题1的解都可在有限步计算后得到。

定理3式（1）不相容的充要条件是在算法中存在正整数k，使得Rk≠O，而Zk＝O。

证明充分性当Rk≠O且Zk≠O时，此时进入外迭代算法，那么式（1）是相容的。因此当Rk≠O，而Zk＝O时，式（1）不相容。

必要性利用反证法。若对任意的正整数k，当Rk≠O时都有Zk≠O，由外迭代算法可在有限步计算后求得式（1）的一组自反和双对称约束解，与题设式（1）不相容矛盾。因此存在正整数k，使得Rk≠O，而Zk＝O，故结论成立。

引理［15］设A∈Rm×n，b∈Rm，线性方程组Ax＝b有解，则Ax＝b的唯一极小范数解在R（AT）中，而且在R（AT）中只有Ax＝b的一个解。

定理4当式（1）相容时，令（H∈Rn×n），在算法中选取初始矩阵满足

那么算法可在有限步计算后得到式（1）的唯一极小范数自反和双对称约束解。

该定理的证明可参考文献［13］。

定理5当矩阵式（1）不相容时，线性矩阵方程组（3）有自反和双对称约束解，若在内迭代算法中选取初始矩阵满足

那么内迭代算法可在有限步计算后得到方程组（3）的唯一极小范数自反和双对称约束解，也就是式（1）的唯一极小范数自反和双对称约束最小二乘解。

证明根据文中所给算法和定理2，若选取内迭代算法的初始矩阵满足式（7），那么内迭代算法可在有限步计算后求得方程组（3）的自反和双对称约束解Y*，且Y*可表示Y*＝g（J1，J2），，J2∈BSRn×n）。

下证Y*是方程组（3）的唯一极小范数自反和双对称约束解。引进记号，ji＝，（i＝1，2）。将Y*＝g（J1，J2）按行拉直可得

因此由引理可得Y*是正规方程组的唯一极小范数解，利用拉直算子vec的同构性，可得Y*是方程组（3）的唯一极小范数自反和双对称约束解，也就是式（1）的唯一极小范数约束最小二乘解。

3 问题2的解

根据自反矩阵与反自反矩阵的正交性、双对称矩阵与对称次反对称矩阵的正交性可得

式（8）右端第2项为固定值，记W＝2，则有

因为上式等号右端2个矩阵的内积为0，所以

上式右端第2项仍为固定值，因此求解问题2等价于在SE求，使得

的极小范数自反和双对称约束解。选取初始矩阵满足式（6），利用算法可求得式（9）的唯一极小范数自反和双对称约束解BSRn×n。

当式（1）不相容时，则求解问题2可等价转化为求解

的极小范数自反和双对称约束最小二乘解。选取初始矩阵满足式（7），利用内迭代算法可求得式（10）的唯一极小范数自反和双对称约束最小二乘解∈BSRn×n。

因此可得问题2的解为

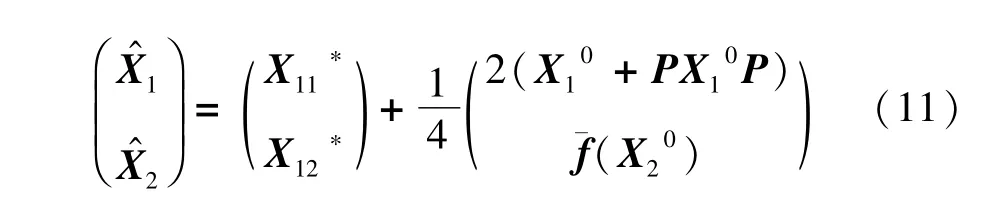
4 数值实验

本节给出2个数值例子来验证算法的可行性和有效性。例1是在式（1）不相容的情况下，求解该方程的自反和双对称约束最小二乘解和极小范数自反和双对称约束最小二乘解、最佳逼近解；例2是在式（1）有自反和双对称约束解且逼近矩阵＝hankel（1∶6），＝toeplitz（1∶6）的情况下，求解式（1）的约束解和最佳逼近解（MATLAB R2014a软件－CPU 3.20GHZ）。

例1令，A1＝2S1，A2＝A1＋3S2，B2＝B1＋S1，A1＝2S1，A2＝A1＋3S2，B2＝B1＋S1，C1＝。选取初始矩阵＝2I，设对称正交矩阵P为单位矩阵且终止准则ε＝10－7。

1）求方程（1）的自反和双对称约束最小二乘解。根据例1所选矩阵结合文中算法，可判断该矩阵方程是不相容的，经过外迭代3次，内迭代3次，即k＝3，k1＝3，可得自反和双对称约束最小二乘解为