基于LBM的旋转车轮整车气动特性研究

胡兴军，李久超，曹庆炜，张扬辉，王靖宇

（吉林大学 汽车仿真与控制国家重点实验室，长春 130022）

在能源危机和环境污染背景下，与汽车相关的节能减排问题越来越受到人们的关注和重视。研究显示，整车阻力的25%～30%来自于轮辐、轮胎等车轮总成［1－2］，因而车轮空气动力学特性的改善对于降低整车气动阻力显得极具意义。

国内外学者围绕汽车车轮气动特性开展了相应的研究。Fackrell等［3］对单车轮旋转的空气动力学特性进行分析，指出旋转车轮比静止车轮阻力和升力系数有所降低。Elofsson P等［4］采用移动地面和旋转壁面研究车轮旋转减阻机理，指出减阻主要原因是后轮旋转尾流改善了车尾流动情况。胡兴军等［5］通过研究不同幅板对车轮空气动力学特性的影响，得到车轮辐板上的开口布置和形状影响整车气动阻力系数的结论。王国华等［6］采用旋转壁面方法研究车轮气动阻力系数变化规律。Christoffer Landström等［7］研究Volvo某款车型不同的轮辐开口面积对阻力的影响，阻力系数最大变化0.22。贾青等［8－9］研究车轮运动状态对车轮和整车气动性的影响，得出车轮旋转会降低阻力和升力，并在一定程度上提高汽车操纵稳定性。Suad Jakirlic等［10］研究了移动地板与车轮旋转对整车空气动力特性的影响，得到车轮旋转会减小阻力的结论，而且车底部的细节也会影响整车的气动特性。Yu Xiaoyan等［11］对比分析了3种旋转方法的优缺点。汽车车轮对整车气动特性影响较大，车轮静止和旋转对整车空气动力学特性影响各不相同。

目前对于整车气动特性的研究大多选取静止车轮进行研究，与汽车真实行驶状态存在一定差异；并且国内研究旋转车轮都是基于传统算法。目前许多计算流体力学软件采用Navier-Stokes方程，在分析的尺度越来越小、流动越来越复杂的环境下，Navier-Stokes方程分析这些现象越来越困难［12］。对于计算模型存在运动和变形的情况，算法需要解决贴体网格的守恒性问题，给算法编程带来难度［13－14］。LBM具有精度高、稳定性好、算法简单、边界易处理等优点。本文采用LBM通过PowerFLOW软件进行仿真求解，对比分析3种车轮旋转方法，并采用复合旋转方法研究旋转车轮整车气动特性。

1 格子玻尔兹曼方法（LBM）

LBM是一种求解流体微观层面上的方法，主要思想是把连续介质划分为多个流体微元，大量的离散点粒子位于网格节点。格子玻尔兹曼方法是通过模拟介观的粒子质量密度分布函数在时间和空间的演化来描述宏观的物理流动［15－16］。在格子波尔兹曼模型中，用粒子分布函数描述流体的宏观运动。粒子分布函数为：

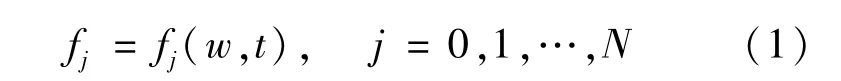
式中：j为格子方向；w为格点位置；t为时间；N为离散速度方向的个数。

计算宏观密度ρ和速度v的公式为：

式中，sj为离散速度矢量。

根据LBGK离散化速度模型，fj随时间演化的方程为：

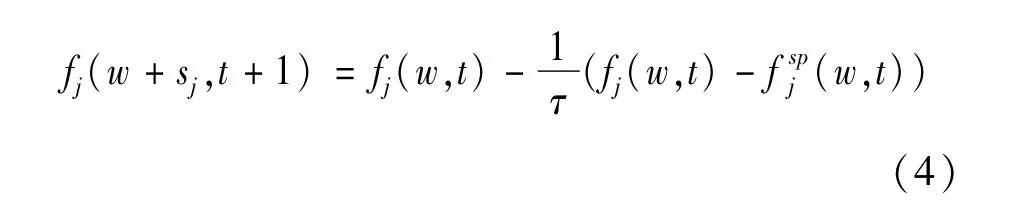
式中：τ为量纲为1松弛时间，表示非平衡态分布向平衡态分布趋近的速度。

2 计算设置

2.1 模型与计算域

数值仿真所采用的模型为1∶1快背式DrivAer模型，如图1所示，坐标原点位于前轴中心点处。车轮的直径为632 mm，车轮轮辐直径为441 mm，胎厚为95.5 mm，胎宽为140 mm，如图2所示。该模型是应用最广泛的空气动力学汽车模型之一，其几何结构简单并能表现出车辆的主要几何结构特征，相关文献资料齐全便于对数据结果进行验证。

图1 DrivAer（快背）示意图

图2 车轮示意图

2.2 网格策略

为准确捕捉造型与提高网格质量，面网格采用三角形网格，在流动关键区域例如A柱、后视镜、窗区域以及前部曲率较大区域、尾流区等区域采用更小的网格尺度，其他区域适当加大面网格尺度，保证面网格过渡均匀。在Powerflow软件进行仿真时，AWT模板下VR区（Variable Resolution region）设置完成VR1～VR5区域，在此基础上根据模型设置VR6～VR8区域，其次为提高计算精度需要在一些产生气流分离的区域布置VR9～VR10，以捕捉到更完整的气流信息，如图3所示。

图3 VR区示意图

2.3 边界条件

入口边界设置成速度入口，速度为30 m／s；出口设置成压力出口，静压为0 Pa；车轮的旋转角速度设置为ω＝94.192 rad／s，车轮低于地面5 mm；地板设置成移动壁面；其余边界设置成对称壁面。仿真步数为100 000，物理时间为0.746 s。根据计算得到数据的收敛情况做向后平均，取得时均值进行分析，仿真计算在48核服务器上进行。

3 数值计算结果分析

3.1 3种旋转方法对比

目前普遍应用的实现车轮旋转的方法有3种：移动坐标参考系（moving reference frame，MRF）、旋转壁面（rotating wall，RW）和滑移网格（sliding mesh，SM）。这3种方法各有优缺点：①MRF在参考系转换时引入了压力梯度，其与体网格速度和旋转矢量叉积成比例［17］，在数值计算上存在误差，且车轮与地面不能接触；②RW不能有效地计算与入口速度垂直面上的流场信息；③SM被认为是仿真旋转车轮较为准确的方法之一，但是滑移网格区域内必须满足旋转对称且该方法无法使车轮接触地面。由于MRF方法和SM方法都无法使旋转车轮接触地面，因此为了在对比不同旋转方法时统一变量，在这一部分将模型高度提升至离地50 mm。

不同旋转方法Cd值及计算时间如表1所示。RW和SM得到的Cd值相近，而MRF得到的Cd值远大于这2种方法。在计算时间上，虽然SM被认为是较为准确的方法，但是由于需要实时更新网格运动，其计算用时最长，RW用时最短。表2为整车各部分阻力值，前后轮和车身的阻力MRF皆大于RW和SM，尤其后轮相差较大。RW的前轮及车身阻力值略大于SM，后轮阻力值略小于SM，2种方法各部分阻力值相差不大。

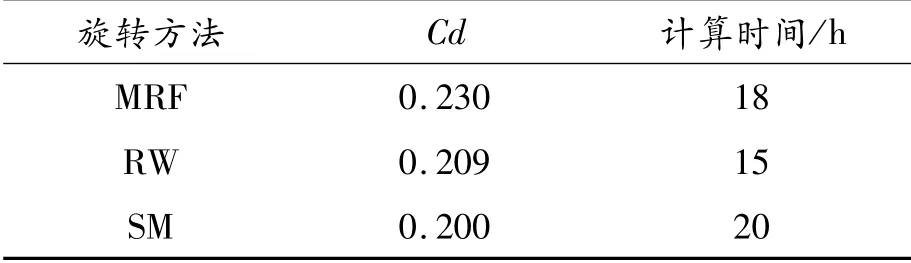
表1 不同旋转方法Cd值及计算时间

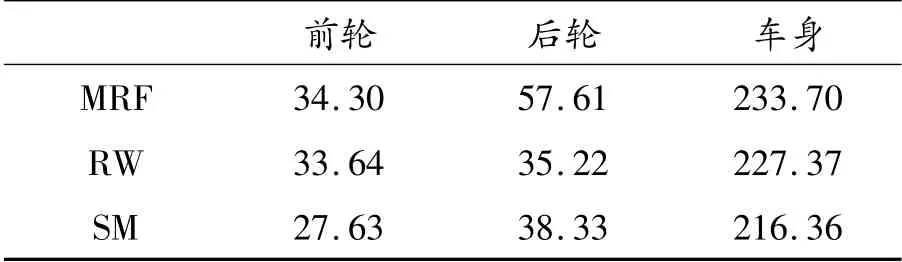
表2 整车各部分阻力值 N

图4为车身底部截面速度分布云图，RW和SM所得结果接近，MRF所得前后轮及车尾分离区域更大。对于前轮，3种方法的车轮前后流动速度相差不大，压差阻力差异较小；而对于后轮，在轮后分离区MRF速度和压力较小，压差阻力较大。

图4 z＝－0.2 m截面速度分布云图（MRF，RW，SM）

图5为前轮后部x＝0.5 m截面速度流线，气流在车轮处发生分离形成分离涡。MRF在车轮中心高度处形成一个尺度较大强涡旋的同时在后视镜下方高度处形成一个尺度较小弱涡旋，且由于位置较高不会受到车轮底部高速气流的影响。而RW和SM只在较低位置形成一个小涡旋，且对于SM该涡旋已基本消失，因此3种方法的前轮涡阻差异较大。

图5 x＝0.5 m截面速度流线（MRF，RW，SM）

图6为后轮后部x＝3.3 m截面速度流线，3种方法皆在车轮中心高度处形成一个分离涡且尺度相近，由于后轮处于前轮尾流之中，来流速度小于前轮，所以分离涡尺度相对较小，3种方法的后轮涡阻差异也较小。

图6 x＝3.3 m截面速度流线（MRF，RW，SM）

图7为左前轮纵向对称面速度分布云图，在车头位置处，三者流动状态基本相同，主要差异在车尾。在车轮处形成的分离涡耗散会消耗车底部高速流体动能，进而影响车底流体在车尾处的流动分离和车尾低压区压力回升。3种方法在前轮处形成的分离涡尺度依次减小，车尾低压区流速和压力回升速度依次升高，车身阻力逐渐减小。

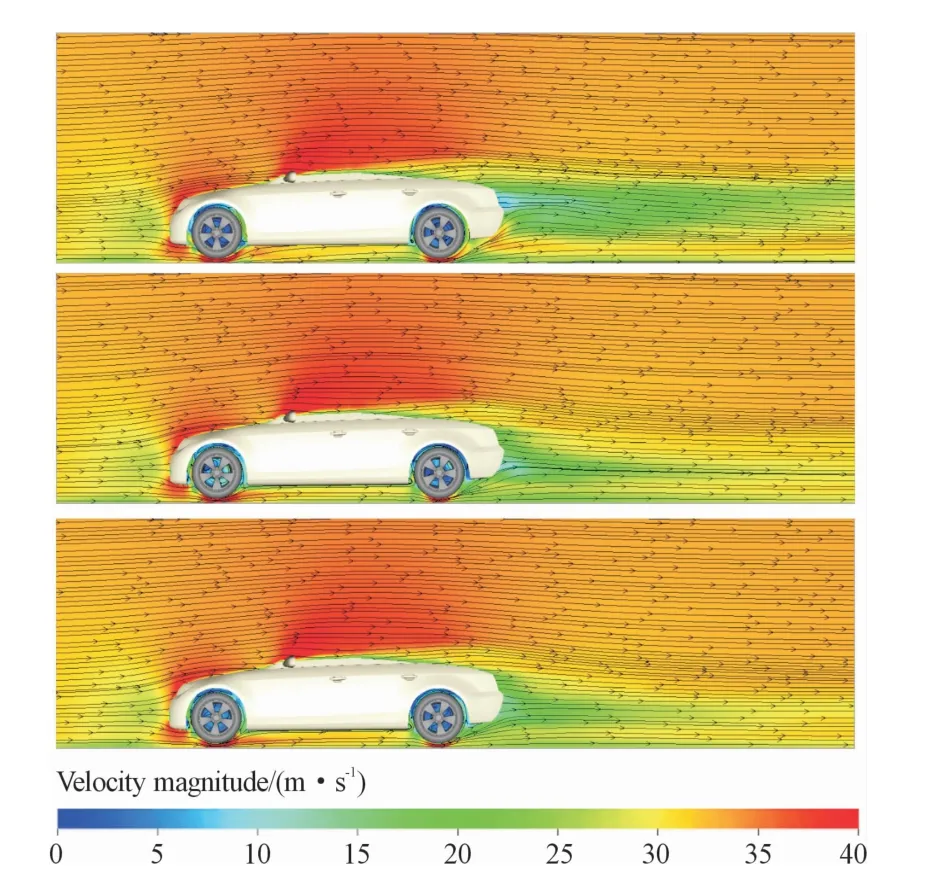
图7 y＝－0.75 m截面速度分布云图（MRF，RW，SM）

3.2 复合旋转方法

单一旋转方法存在以下不足：①MRF和SM无法使车轮接触地面旋转；②MRF由于引入压力梯度存在一定误差；③RW无法有效计算与入口速度垂直面上的流场信息；④SM须实时更新网格运动，耗费计算资源。为弥补单一旋转方法的不足，采用复合旋转方法实现车轮旋转，车轮轮辐设置为SM，车轮轮胎设置为RW（下文简称SMRW方法），并与实验值对比验证仿真方法准确性，参考实验值来自于文献［18］。

如表3所示，SMRW方法计算Cd值与实验值相差3个Count，相对误差为1.23%。仿真方法具有较好的准确性，且计算效率相对于SM提高15%。接下来采用SMRW方法研究旋转车轮整车气动特性，并与静止车轮工况进行对比分析。

表3 复合旋转方法Cd值

由图8可知，随着来流风速的升高，车轮旋转与静止时的Cd值均逐渐减小，且在各风速下车轮旋转相对于静止Cd值均减小约20个Count，减阻效果明显。表4为整车各部分阻力值，车轮旋转时，前轮和车身阻力均小于车轮静止，阻力分别减小12.7%和7.9%，而后轮阻力增加32.9%，整车阻力减小5.9%。由于后轮处于前轮尾流之中，来流速度较小，所以车轮静止与旋转时的后轮阻力均小于前轮。

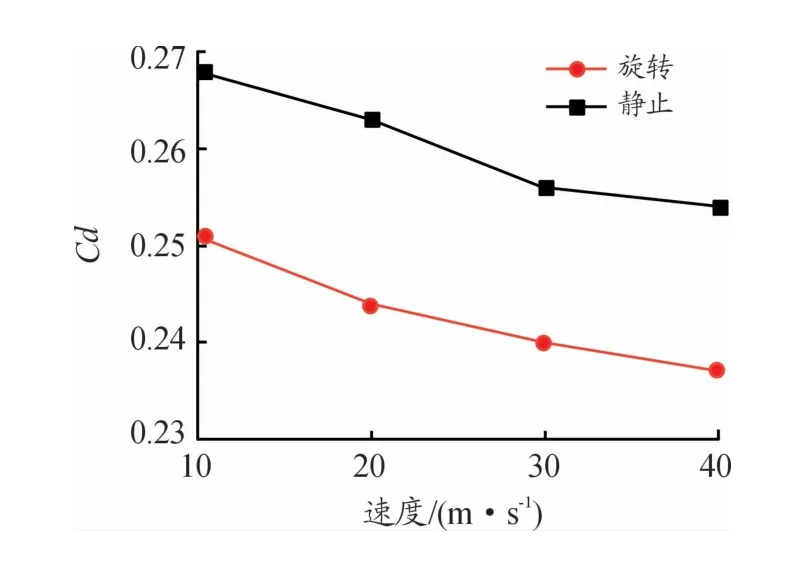
图8 不同来流速度Cd值

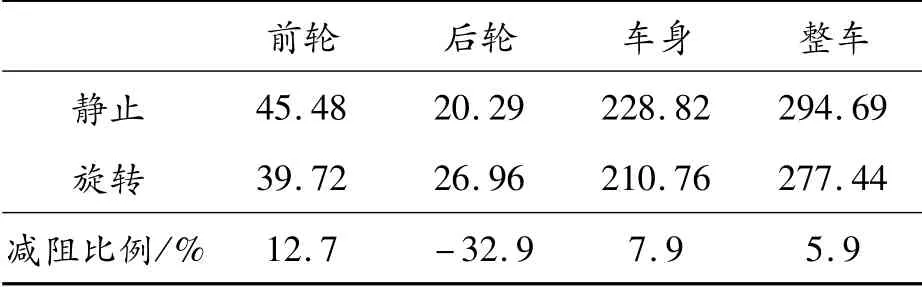
表4 整车各部分阻力 N

由图9可知，对于前轮，车轮静止时分离区流速和压力较低，而车轮旋转会提高车轮表面气体动能，加快分离区压力回升速度，从而减小压差阻力；对于后轮，由于处于前轮尾流之中，来流速度较小，车轮旋转对于其尾流速度影响较小；对于车身底部高速气流，一方面由于车轮静止时前轮分离涡尺度较大，消耗气流动能较大，另一方面因为车轮旋转提高气流动能，车轮旋转时车底气流流速更高，可以延迟车尾底部气流分离，加快分离区压力回升，减小车身压差阻力。

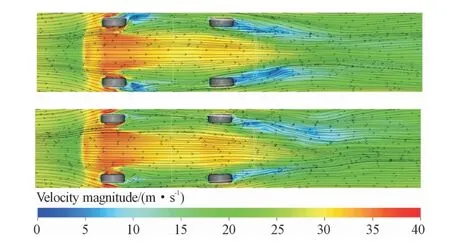
图9 z＝－0.2 m截面速度云图（静止，旋转）

由于前轮来流速度方向偏向车轮外侧，导致前轮分离涡偏向车轮外侧；由于车底气流流速较高、压强小，气流流向逐渐偏向内侧，后轮分离涡稍向车轮内侧偏移；由于在车轮旋转时，前轮分离涡尺度较小，且车底气流流速更高，内侧压力更小，所以后轮来流速度方向向内侧偏移较多，后轮迎风角更大，分离区也更大，压差阻力更高。

由图10可知，车轮静止时，在前轮中心高度处形成一个大尺度强分离涡，大尺度涡旋上下各有一相反方向小尺度弱涡，而在车轮旋转时，带动两侧气流加速并上扬，气流方向与大尺度涡旋转方向相反，使强涡旋尺度减小，2个弱涡旋基本消失，且由于上扬高速气流的挤压作用，强涡旋位置降低，接近地面与地面摩擦加速耗散。由图11可知，车轮旋转时分离涡位置更加靠近内侧，这也验证了图9所得结果。

图10 x＝0.5 m截面速度流线（静止，旋转）

图11 x＝3.3 m截面速度流线（静止，旋转）

结合图12和图13可知，前轮分离区偏向车轮外侧，且车轮旋转时，前轮分离区尺度更小；车轮静止时后轮分离区基本位于车轮后方，而车轮旋转时后轮分离区偏向车轮内侧；后轮旋转带动气流上扬加速，使车尾底部气流流速增加，加快车尾分离区压力回升，减小车身压差阻力。

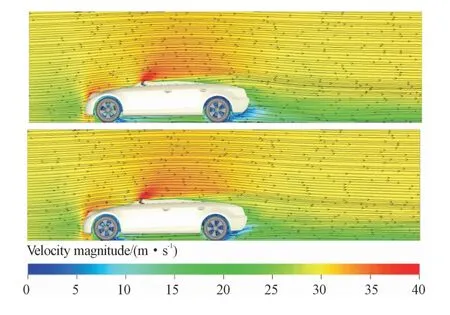
图12 y＝－0.75 m截面速度云图（静止，旋转）

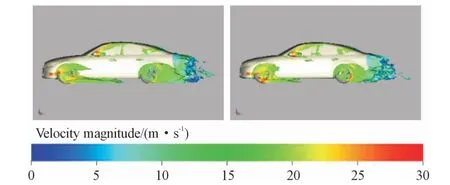
图13 Cpt＝0等值面（静止，旋转）

3.3 不同尾部造型气动特性

对不同背部造型DrivAer模型旋转车轮整车气动特性进行研究。整车模型如图14所示。仿真设置与快背式模型分析保持一致。

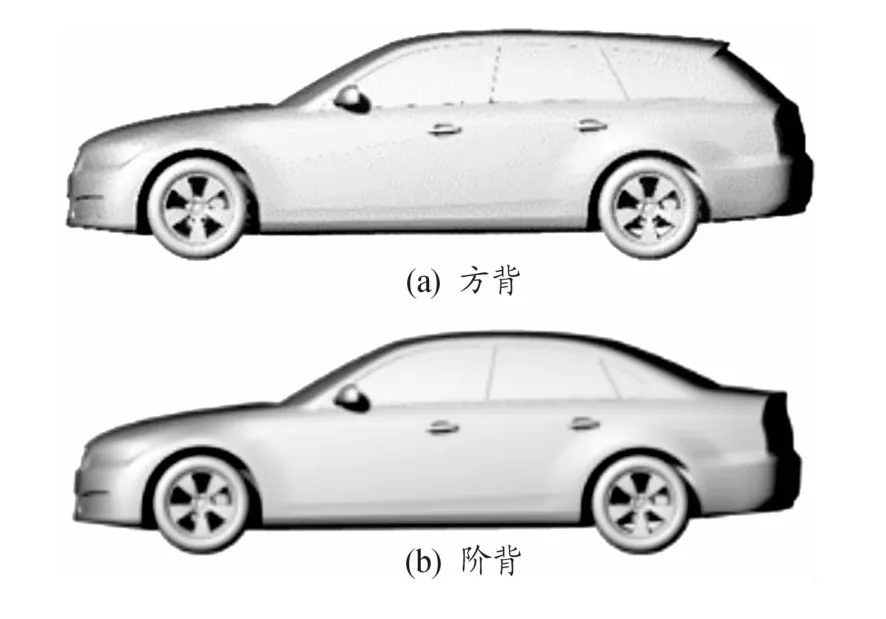
图14 Drivaer模型（方背，阶背）

由图15可知，对于方背和阶背式模型，各风速下车轮旋转Cd值均小于车轮静止。方背式模型在低速时Cd值减小约13个Count，在高速时减小约20个Count，而阶背式模型在各风速下车轮旋转Cd值均能减小20个Count。

图15 不同速度下阻力值

由表5和表6可知，方背和阶背式模型得到与快背式模型趋势相似的结果，车轮旋转时前轮和车身阻力减小，后轮阻力增加；阶背式模型前轮阻力减小比例最大，方背式模型后轮阻力增加比例最小，3种模型车身阻力减小比例相近；阶背式模型整车减阻比例达到9.7%。

表5 整车各部分阻力（方背） N

表6 整车各部分阻力（阶背） N

结合图16～19可知，方背和阶背式模型旋转车轮对整车气动特性的影响机理与快背式车型基本一致，可以简要总结为以下几点：

图16 z＝－0.2 m截面速度云图（静止，旋转）

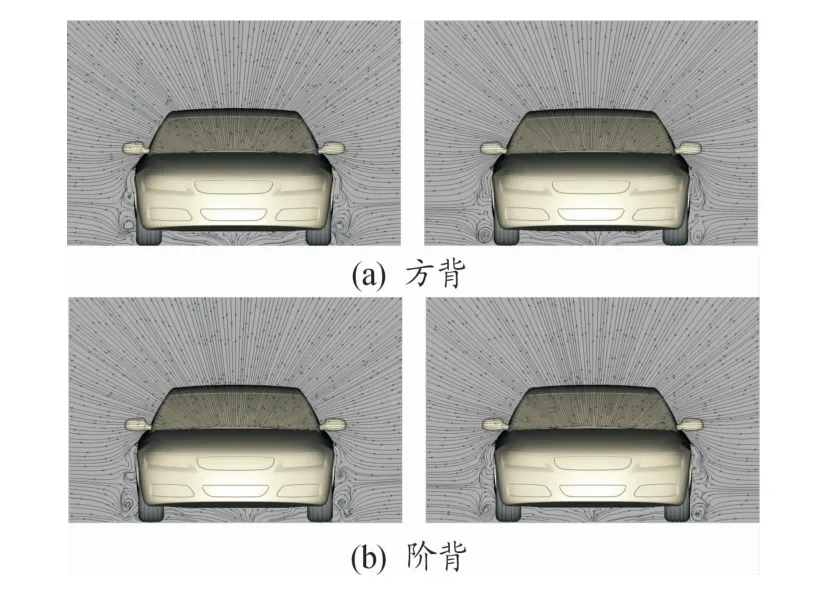
图17 x＝0.5 m截面速度流线（静止，旋转）

图18 x＝3.3 m截面速度流线（静止，旋转）

图19 y＝－0.75 m截面速度云图（静止，旋转）

1）对于前轮，车轮旋转会提高车轮表面气体动能，加快分离区压力回升速度，减小压差阻力；

2）车轮旋转带动两侧气流加速并上扬，可以减小分离涡尺度，减小涡阻；

3）车轮旋转时车底气流流速更高，可以延迟车尾底部气流分离，加快分离区压力回升，减小车身压差阻力；

4）车轮旋转时，后轮来流速度方向向内侧偏移较多，后轮迎风角更大，压差阻力更高；

5）后轮旋转带动气流上扬加速，使车尾底部气流流速增加，加快车尾分离区压力回升，减小车身压差阻力。

4 结论

1）SMRW方法计算Cd值与实验值相差3个Count，相对误差为1.23%，仿真方法具有较好的准确性，且计算效率相对于SM提高15%，可以很好地弥补3种单一旋转方法的不足。

2）车轮旋转时，整车Cd值在各风速下均小于车轮静止时。方背式模型在低速时Cd值减小约13个Count，在高速时减小约20个Count，而快背和阶背式模型在各风速下Cd值均能减小20个Count。

3）3种背部造型模型在车轮旋转时，前轮和车身阻力均下降，后轮阻力均上升，变化比例各有差异，整车减阻比例分别为5.9%、5.9%、9.7%。

4）旋转车轮主要影响车轮周围流场、车身底部流场以及车尾分离区。