基于蒙特卡洛重要抽样法的结构时变可靠性分析

2021-07-14严宇飞李方义

重庆理工大学学报(自然科学) 2021年6期

严宇飞，李方义

（1.长沙理工大学汽车与机械工程学院，长沙 410114；2.长沙理工大学桥梁工程安全控制省部共建教育部重点实验室，长沙 410114；3.广州大学机械与电气工程学院，广州 510006）

在实际工程问题中，结构在工况下会受到材料性能退化、随机载荷过程等不确定因素的影响，且这些因素往往具有时变效应，导致其结构可靠性动态变化。因此，针对结构动态可靠性的研究是很有必要的。结构时变可靠性分析就是一种动态结构可靠性分析，它符合实际工程所需，能够客观、准确地对某工件或结构的可靠性进行预测或评估。当前结构时变可靠分析已有不少研究成果，如：基于跨越率方法［1］演变的“PHI2方法［2－5］”、基于“时间离散”的方法［6］总结的“准静态法［7－9］”等。然而与MCS相比，当用上述方法求解非线性较强的结构可靠性问题时，都有着求解复杂或求解精度不足的缺陷。

MCS求解结构可靠性问题时，其求解精度仅与模拟次数有关，模拟次数越多，其精度越高，且与问题的维数无关。因此，MCS理论上可以求解所有的可靠性问题。MCS在结构时变可靠性问题的应用上有：王帅等［10］应用MCS求解时域－误差模型的运动时变可靠性；Li［11］基于MCS模拟得到电车轨道连接螺栓工作载荷的概率分布，以分析连接螺栓的结构时变可靠性；Li等［12］利用MCS验证其求解混合变量的时变模型结果的准确性；Wang等［13］利用MCS验证其提出的方法求解结构时变可靠性问题的准确性等。但是由于MCS随着模拟次数的增加，会导致计算量越来越巨大。因此，由于MCS的计算效率一般来说是比较低的，从而MCS通常被用来验证结果。

由于MCS具有高的求解精度，因此要将MCS应用于结构时变可靠性问题上就一定需要考虑改善并提高MCS的计算效率的问题。当前研究者针对这一问题引入了重要抽样法［14－15］来提高MCS的计算效率。“重要抽样法”指的是在模拟次数一定的情况下，通过改变抽样中心的位置或用新的概率分布对随机变量进行抽样，来估计失效概率的方法。又由于在结构时变可靠性问题上，重要抽样法的应用存在着反应量的概率密度函数未知的问题和抽样函数需求的时间多维联合概率密度函数难以获得的问题［16］，因此当前重要抽样法主要是应用在静态的结构可靠性问题上，而应用在结构时变可靠性问题上的研究成果寥寥无几，Prablwarter等［17－18］基于俄罗斯轮盘赌、分裂方法对蒙特卡洛重要抽样法进行研究，但该方法对计算机运算能力的要求比较高；宋晓通和谢绍宇等［19－20］在电力系统可靠性评估上提出了自适应重要抽样算法，但该方法应用于其他领域上时，还需要进行一定的改善；罗立胜［21］以串联理论处理时间变量，提出了一种锈蚀钢构件时变可靠度的重要抽样法，但对该方法的普遍适用性未进行探究。因此，针对结构时变可靠性问题，研究一种精度好、理论简单、计算简便的蒙特卡洛重要抽样方法是很有必要的。

本文将“蒙特卡洛重要抽样法”应用于结构时变可靠性问题之中，并结合“准静态法”和“FOSM”，提出一种基于蒙特卡洛重要抽样法的结构时变可靠性分析方法，使得本文方法不仅能够达到接近MCS的求解精度的程度，而且与MCS相比，求解效率也有很大提高。本文给出本文方法的计算原理和具体的计算步骤，并以MCS、FOSM以及本文方法对3个算例分别进行计算，通过3种方法的求解结果对比，证明本文方法的优越性，为蒙特卡洛重要抽样法应用于结构动态可靠性分析上提供新的方法和思路。

1 结构时变可靠性模型

通常来说，大多结构时变可靠性模型的研究都是基于广义的抗力模型，其极限状态方程Z（t）一般由结构抗力随机过程R（t）和载荷效应随机过程S（t）组成的线性或非线性函数方程，其表达式为：

式中：t为时间变量；载荷效应随机过程S（t）一般含有永久载荷A（其通常为n维的随机向量）和可变载荷随机过程Q（t），即式（1）改写为：

在实际工程问题中，结构抗力随机过程R（t）的常见的退化形式有指数退化形式、对数退化形式等，具体如下：

指数退化形式表达式：

对数退化形式表达式：

其中：R0为初始抗力；ε为衰减系数。

由可靠度定义知结构在设计使用期T内结构可靠度Ps（t）和失效概率Pf（t）为：

2 重要抽样法理论

MCS生成的随机变量样本点多集中在联合概率密度函数的最大值点附近，但实际上结构失效是个小概率事件，从而在失效域内获取到样本机会小，导致MCS的求解精度较低，因此MCS要大量的样本来提高算法精度。蒙特卡洛重要抽样法是通过改变随机抽样的中心，使得样本点更有可能落在失效域中，使得模拟次数适量减少也可保证算法求解精度和效率。

设X＝（X1，X2，…，Xn）是结构的随机变量，其概率分布为fX（x），Z＝g（x）为功能函数，结构失效概率Pf为：

式中I［g（x）］为g（x）的指示函数，表示为：

随机变量X的第i个样本向量表示为：xi＝（xi1，xi2，…，xin），则结构失效概率Pf的期望估计值为：

根据文献［22］可知，通过改变抽样方式，抽取的样本点更可能落入失效域内或所谓的重要区域内，使得求解精度提升。因此，式（7）可改写为：

式中px（x）为：“重要抽样函数”，即取代fx（x）对X抽样的函数。此时，Pf的期望估计值为：

3 基于蒙特卡洛重要抽样法的结构时变可靠性分析方法

蒙特卡洛重要抽样法中样本点的选择通常是在随机变量的均值最大可能点或由FOSM得到的MPP点附近选取［23］。

将其应用于结构时变可靠性问题时，首先必须先对时间变量进行处理，使得动态可靠性问题变为静态可靠性问题。因此，利用文献［6－9］中的方法将设计基准期T划分为m个均匀相等的时段，即每一个时间段为τ＝T／m，如图1所示，此时可将抗力随机过程R（t）和动载荷随机过程Q（t）离散化处理，得到m个随机变量Ri和Qi，以第i个时段抗力的中值为Ri，将式（5）转化为：

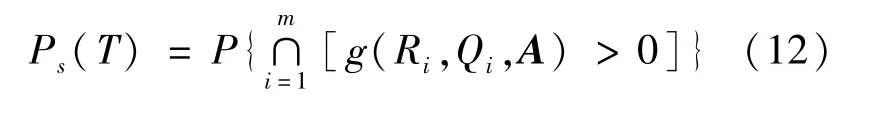
图1 抗力R（t）与可变载荷Q（t）随时间的变化曲线

Qi的值是通过所在时间段内的统计得到，通常情况下，可将Qi视为独立同分布的。因此，由串联体系可靠度理论可将式（6）改写为：

从工程意义方面考虑，不妨将Q′取为m个Qi的最大值QT。同时，Qi是独立同分布的，根据统计学的原理，设计基准期T内最大载荷效应QT的概率分布函数FQT（x）为：

在实际问题中，通常情况下将载荷效应Qi近似为以参数为ατ和μτ的极值I型分布，因此QT也将服从参数为αT和μT的极值I型分布，即：

引入新的随机变量Q′，其概率密度函数为fQ′（q′），概率分布函数为FQ′（q′），式（13）可转化为：

式中：fR1，R2，…，Rm（r1，r2，…，rm）是R1，R2，…，Rm的联合概率密度函数；fA（a）为A的概率密度函数；FQr为Qi的概率分布函数；F－1Q′是FQ′的反函数。

此时，功能函数转化为：

引入的随机变量Q′没有规定它的分布的类型，事实上，在以式（17）为功能函数利用一次2阶矩法（FOSM）的迭代公式计算可靠指标时，公式中只含有FQ′（Q′）项，这时可将其作为一个变量使用，也就是说整个分析过程与Q′的具体分布无关。但为与现行的结构可靠度设计统一标准相协调，使Q′具有工程意义，将Q′取为m个Qi的最大值QT，因此可将式（17）转化表示为：

由于最大可变载荷效应QT服从极值Ⅰ型分布，因此由式（18）可推导得最终的极限状态方程：

FOSM对式（19）进行计算求解，得到各随机变量对应的MPP点。以对应的MPP点进行蒙特卡洛重要抽样，得到各随机变量的样本点，并将其代入式（2）中进行计算，统计功能函数失效的次数nf，然后以Pf＝nf／n得到结构的失效概率，最后求得结构的可靠度指标。

本文方法具体步骤及流程（见图2）如下：

图2 算法流程框图

1）以“准静态法”对结构时变可靠性模型进行处理，离散时间T为m段，使得随机过程等效为随机变量，并求出每段中的广义抗力Ri和载荷QT，使得动态可靠性问题变为静态可靠性问题；

2）在ti时间段内，利用FOSM的方法对处理后得到的结构时不变可靠性模型进行计算，得到随机变量相对应的MPP点xi；

3）在xi附近对随机变量进行重要抽样法采样，样本容量为n；

4）将得到的样本数代入式（2）之中计算，统计功能函数失效的次数nf，以Pf＝nf／n得到ti时间段内结构的失效概率，又通过失效概率可求出ti时间段内的结构的可靠度指标。

4 算例分析

为验证本文方法的精度和效率，将其应用于下列3个算例之中，通常情况下的，MCS的样本容量为：n＝106～108。

4.1 某机械零件

已知某机械零件［24］的抗力随时间的变化规律为R（t）＝R0exp（－at）MPa，a为衰减系数，其值为2×10－5，初始抗力R0服从（μR0σR0）MPa的对数正态分布，永久载荷效应A服从（μA，σA）MPa的正态分布，如表1所示，以τ＝1 000 h作为一个时间段，动态载荷Q（t）在第i个时间段内的统计值Qi服从参数为ατ和μτ的极值I型分布，其中参数ατ＝0.044 93 MPa－1，μτ＝49.77 MPa。计算该零件在不同设计基准期时的可靠度指标。

表1 某机械零件的随机变量分布情况

当设计基准期为5 000 h时，对比MCS、FOSM以及本文方法3种方法求解结果，其中本文方法模拟次数分别从104、5×104、105、106进行试验计算，同时为减小偶然误差，均反复进行了10次运算。其中，当模拟次数为104时，最大误差达到了0.63%；5×104时，最大误差达到了0.51%；105时，最大误差达到了0.50%；106时，最大误差达到了0.38%，且随着模拟次数的增多，结果值趋近且稳定。因此，本文选取模拟次数为5×104进行分析，其结果值相对误差在0.29%～0.63%，表2中本文方法可靠度指标和相对误差取10次运算后的平均数，具体如下：

表2 设计基准期5 000 h时某机械零件的求解结果

误差1是指FOSM与MCS之间的误差；误差2是指本文方法与MCS之间的误差。

结果分析：考虑到参数的时变特性，求解某机械零件在10个设计基准期内的可靠度指标。从表2结果所示可知：本文方法仅用5×104的样本数就能与MCS的结果接近，模拟次数仅为MCS的1／20，因此本文方法的求解效率与MCS相比，求解效率有明显提高。从表3结果所示可知：随着设计基准期的延长，结构或产品的可靠度指标逐步下降，这完全符合实际情况。同时，从表4结果所示可知：在设计基准期内，FOSM的最大误差为0.92%，而蒙特卡洛重要抽样法的最大误差为0.91%，均在误差允许范围内。同时，从误差1与误差2的对比中可以发现：本文方法的精度更高、更准确，说明本文方法求解结构时变可靠性问题是有效且精度较高的。

表3 某机械零件各设计基准期的可靠度指标

表4 某机械零件各设计基准期的结果误差

4.2 某结构的钢筋混凝土短柱

某地方某结构［6］的钢筋混凝土短柱的截面尺寸宽和高分别为b和h，其参数值分别为300、375 mm。混凝土的强度等级为C30，柱内钢筋面积As＝1 811.28 mm2，使用的钢筋是Ⅱ级钢筋。钢筋混凝土短柱受抗力随机过程为R（t），永久荷载效应G以及可变荷载效应Q影响，其中抗力随机过程为R（t）与混凝土抗压强度fc和钢筋屈服强度fy有关，最大可变荷载效应QT服从极值Ⅰ型分布，具体参数和分布见表5，假设设计基准期为T＝50年。其他未提及系数默认为确定性参数，计算该柱的可靠指标和失效概率。功能函数为：

表5 某结构的钢筋混凝土短柱的随机变量分布情况

钢筋混凝土柱的抗力R（t）与混凝土抗压强度fc和钢筋屈服强度fy的关系如下：

查得该地方的抗力变化系数φc（t）和φy（t）为：

当设计基准期为25年时，同4.1处理。对比MCS、FOSM以及本文方法3种求解结果，本文方法结果值相对误差在0.19%～1.30%，具体见表6。

表6 设计基准期25年时某结构的钢筋混凝土短柱的求解结果

结果分析：本算例一共预设了10个设计基准期，从表7所示可知，随着设计基准期的延长，某结构的钢筋混凝土短柱的可靠度指标逐步下降。同时，在设计基准期内，FOSM的最大误差为2.03%，而蒙特卡洛重要抽样法的最大误差为1.07%，这都是在允许误差范围内。从表8可知：FOSM结果误差偏离的更多，对比算例4.1，算例4.2中的FOSM求解精度降低许多，说明FOSM虽然可以满足求解的需要，但由于其仅适应独立正态分布的变量，使得运算中需要有正态空间的转化以及偏导，从而产生误差，又由于功能函数的近似处理和原时变可靠性问题的近似处理，使得FOSM求解精度会有所降低。而MCS由于大的模拟次数，能够保证该方法求解精度，因此MCS的精度会高于FOSM。又从误差1与误差2的对比中发现：FOSM精度存在着不稳定且精度一般的问题，而本文方法的精度依然较高，且计算精度比较稳定，表6可进一步证明本文方法相对MCS，效率明显有所提高。因此，说明本文方法对于结构时变可靠性分析来说是一个有效的且能够保证精度的方法。

表7 某结构的钢筋混凝土短柱各设计基准期的可靠度指标

表8 某结构的钢筋混凝土短柱各设计基准期的结果误差

4.3 屋顶的桁架结构

图3所示是根据文献［25］改编的一个屋顶的桁架结构，底部和承拉的杆件材料为钢，顶部和承压的杆件用水泥加固。屋顶承受均匀的分布载荷q（t），q（t）可以转化成等效的节点力P＝q（t）l／4，节点C处的垂向位移可以推导为：

图3 屋顶桁架模型

其中：AC和AS分别表示水泥杆和钢制杆件的截面积，其数值分别为0.034 m2和0.000 94 m2；EC和ES分别表示它们的弹性模量。

受载过程中，节点C位置的垂向位移应小于D（t），且随时间衰减，其衰减规律为D（t）＝D0［1＋ln（1－0.000 2t）］，其中D0为初始位移。表9列出了此问题中随机变量的具体情况。功能函数定义为：

表9 屋顶的桁架结构的随机变量分布情况

当设计基准期为5年时，同上处理，对比MCS、FOSM以及本文方法3种方法求解结果，其中本文方法结果值相对误差在0.01%～0.37%之间，具体见表10：

表10 设计基准期5年时屋顶的桁架结构的求解结果

结果分析：本算例一共预设了10个设计基准期，由表11可知，随着设计基准期的延长，屋顶桁架结构的可靠度指标逐步下降。同时，在设计基准期内，FOSM的最大误差为2.31%，而蒙特卡洛重要抽样法的最大误差为1.11%。很明显，本文方法的精度远高于FOSM，且本算例中FOSM出现了和算例4.2一样的情况。从表12分析可知：FOSM明显存在着结果不稳定且精度一般的问题。而本文方法的精度仍然较高，且计算结果比较稳定。同时，根据表10中的结果可证明本文方法相比MCS，效率明显有所提高。因此，可以说明本文方法对于结构时变可靠性分析是一个有效的方法。