车辆减振器Kriging模型的结构参数寻优及试验验证

陈 宝，王 涛，李仕生，付江华，黄剑鸣，陈哲明

（1.重庆理工大学 车辆工程学院，重庆 400054；2.重庆汽车动力系统测试工程技术研究中心，重庆 401120）

悬架是车架与车桥之间的一切传力连接装置的总称，是现代汽车上重要的总成之一［1］，其性能对汽车的平顺性具有重要影响。而车辆悬架的主要阻尼元件是减振器，它与悬架弹性元件并联于车身和车轮之间，减振器的阻尼力能有效地衰减簧上、簧下质量的相对运动，提高车辆的行驶平顺性和操纵稳定性。目前应用最广泛的减振器是液压筒式减振器，其阻尼力主要受到减振器结构参数和油液参数影响，油液参数主要指油液黏度，该参数的调整困难［2］，而国内外对减振器结构参数还没有准确、可靠的设计，基本都是以线性刚度和阻尼为前提下，确定阻尼的范围后根据经验和反复试验修改确定［3－4］。因此，有必要研究结构参数对阻尼力的影响和优化设计。合理的结构参数设计能很好地改善汽车的平顺性和舒适性。

Isight是一款多学科多目标优化设计的旗舰产品，广泛应用于航空航天、汽车、电子及船舶领域的优化设计［5］。在对减振器结构参数进行优化设计中，Isight软件根据需要求解最优影响阻尼力的参数，通过内部集成的优化算法输出参数。将这些参数输入Matlab中建立的减振器模型进行运算，运算结果返回到Isight自带集成将进行的优化算法中对相应参数进行优化，从而得到最优的可行性方案。大幅度提高优化设计效率，降低优化设计成本，同时将自行优化设计、自行优化结果分析融为一套流程，减轻优化设计的工作量。

1 减振器数学模型的建立

为了简化计算，提出以下假设［6］：假设活塞环与工作缸、活塞杆与导向座之间没有泄漏；拉伸、压缩工作过程中，减振器内的油液温度保持不变；忽略压力变化引起的系统刚性构件的弹性变形和温度变化对阻尼特性的影响；不计节流过程中产生的油汽泡所耗用油液的质量；不考虑工作油液重力势能的影响；所研究的闭区域内同一瞬时的压力处处相等；除了复原阀及压缩阀节流阀片、复原阀及压缩阀阀片、流通阀及补偿阀阀片上的压力降之外，其他地方的流体能量损失忽略不计。

液压筒式减振器的工作原理分为压缩和复原2个行程。在减振器运动过程中，复原和压缩行程阻尼力可由各节流压力乘以相应承压面积得到。根据假设条件以及流体力学知识，对筒式液压减振器2个行程分别建立开阀前后的数学模型。

1.1 复原行程数学模型的建立

复原行程的工作原理如图1所示。

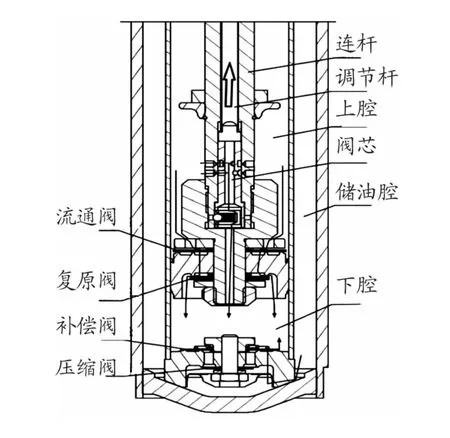
图1 复原行程工作示意图

上腔的油液经过复原阀流入下腔，而储油腔的一部分油液经过补偿阀流入到下腔，油液经过复原阀和补偿阀产生节流压力。当减振器运动速度低于复原行程开阀速度时，复原阀不开阀，油液流经常通节流孔而产生节流压力，当减振器速度大于复原行程开阀速度时，复原阀开阀，油液流经常通节流孔及节流阀片所形成的节流缝隙，产生节流压力。

1.1.1 开阀前

根据假设，减振器在工作中不会有任何油液的泄露，此时的油液流动可视为先从上腔经过活塞的节流孔，再通过活塞下端中的常通孔流入到下腔，则上下腔的压差为：

式中：P11为活塞中间小孔的节流作用形成的压差；P12为常通孔中的缝隙节流产生的压差［7］。

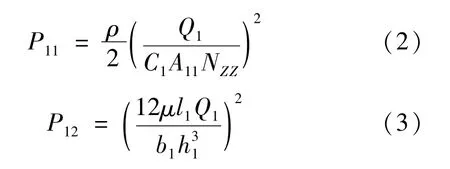
式中：ρ为油液密度；μ为油液的动力黏度；C1为压力损失系数；A11为活塞复原孔截面积；N11为节流孔数目；l1、b1、h1分别为复原节流阀片缺口的长、宽、高。

上腔流到下腔的流量：

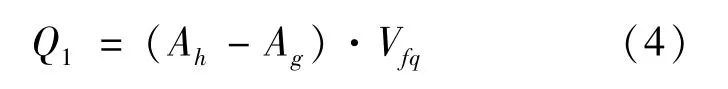
综上可得，开阀前减振器的复原阻尼力为：

式中：Ah为活塞端面积；Ag为活塞杆截面积；Vfq为复原行程开阀前活塞相对减振器工作缸的运动速度。

1.1.2 开阀后

活塞运动速度提高，工作缸上腔的压力越来越大，当复原阀片上的压力等于复原弹簧的预紧力时，复原阀打开，开阀后油液流经流通阀流量：

式中，Vfq为复原行程开阀后活塞相对减振器工作缸的运动速度。

复原行程开阀后压差为：

式中：P21为活塞上小孔节流产生的压差：

P22为复原阀片变形产生和活塞油线间凸起导致的缝隙节流产生的压差：

式中：A12为复原阀片受力面积；b21为活塞体下端凸起的内圈周长；kf为复原弹簧刚度；Ff为复原阀弹簧的预紧力；δ为复原阀开度。

综上可得，开阀前减振器的复原阻尼力为：

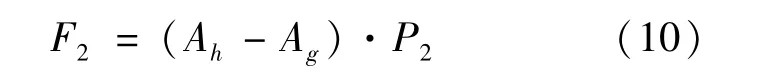
1.2 压缩行程数学模型的建立

压缩行程的工作原理如图2所示。

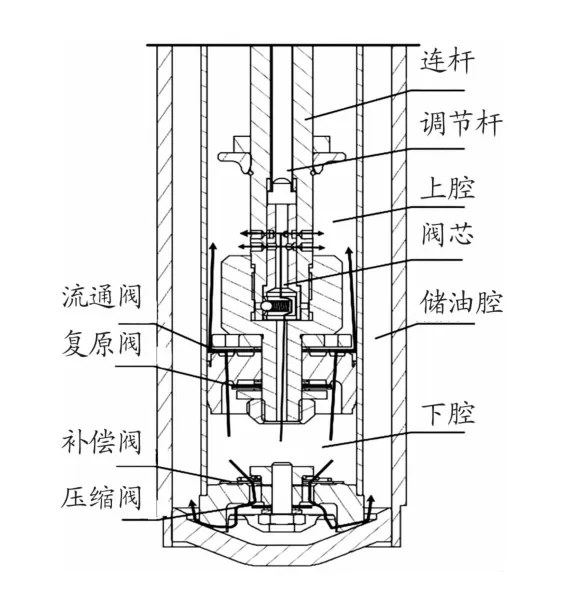
图2 压缩行程工作原理示意图

下腔的一部分油液经流通阀流入上腔，储油腔的部分油液经压缩阀流入储油腔，油液经过压缩阀和流通阀产生节流压力。当减振器运动速度低于压缩行程开阀速度时，压缩阀不开阀，油液仅流经常通节流孔而产生节流压力，当减振器速度大于压缩行程开阀速度时，压缩阀开阀，油液流经常通节流孔及压缩阀片所形成的节流缝隙，产生节流压力。

1.2.1 开阀前

油液先从下腔通过底阀座的节流小孔，再流过压缩阀的常通孔，油液流经压缩阀的流量：

开阀前底阀座的压差：

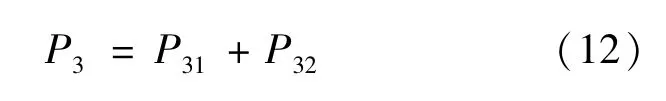
由流体力学的理论公式［8］：

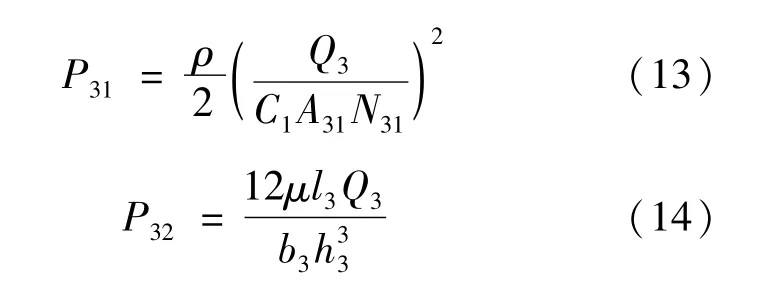
式中：Vvq为压缩行程开阀前活塞相对减振器工作缸的运动速度；A31为流通孔截面积；N31为流通孔数；l3为活塞下端的凸起宽度；b3为压缩阀节流阀片缺口总长度；h3为压缩阀节流阀片缺口高度。

由活塞受力平衡方程可得减振器开阀前的阻尼力为：

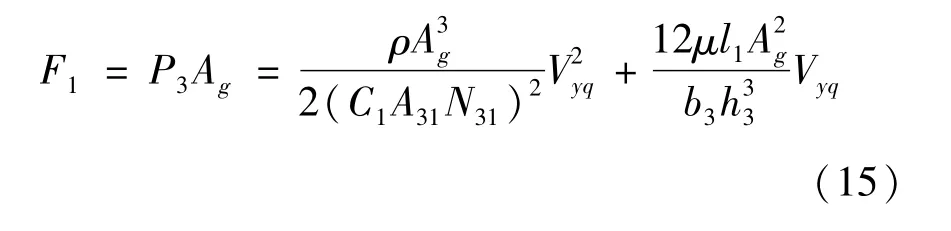
1.2.2 开阀后

活塞运动速度提高，工作缸下腔压力增加，当底阀座组件的压缩阀上的压力等于预紧力时，压缩阀产生变形并被打开，油液流经压缩阀的流量为：

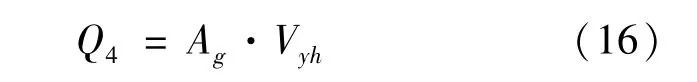
此时，底阀座上下的总压差为

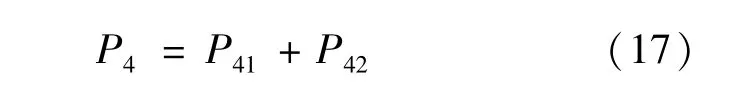
P41为底阀座上的节流小孔产生的压差，为

式中：A41为压缩阀孔截面；N41为压缩阀孔数。由于有常通孔和压缩阀片预紧力的存在，因此

联立式（15）与式（18）解得：

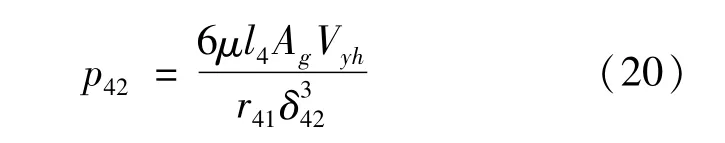
式中：r41为底阀座下端凸起的内半径；l4为压缩阀体下端的凸起宽度；δ42为压缩阀开度。

综上可得，开阀后减振器的压缩阻尼力为：

将上述各式联立即可在Matlab中建立液压筒式减振器的数学模型。

1.3 仿真模型的试验验证

减振器动态特性测试在MTS849减振器试验台上完成，台架实物如图3所示。

图3 试验测试图

减振器试验台采用正弦信号对减振器进行测试，使减振器在固定行程做往复运动，试验台记录该过程中减振器的阻尼力与位移。

减振器试验的活塞行程为25 mm，试验温度为20℃，对比分析减振器在各速度点下试验与仿真数据，对比结果见表1（保留到小数点后1位）。

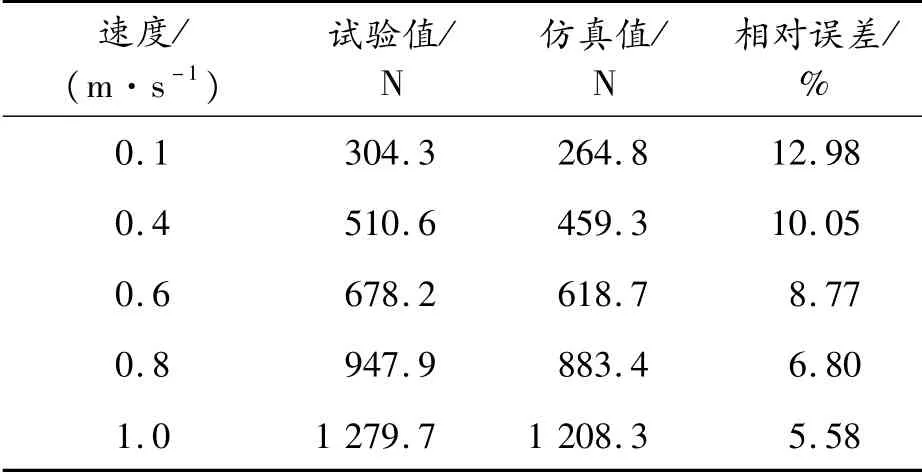
表1 仿真与试验数据对比

根据QC／T491—2018汽车减振器试验标准，相对误差合理的范围为（±13%＋30）N。

从表1的相对误差可看出，仿真与试验结果间具有较高的吻合性，说明建立的模型准确可靠。因为在低速时摩擦力对误差影响相对较大，所以相对误差与测试速度呈反比。

2 减振器结构参数的优化

考虑到活塞参数的改变不易进行试验验证而压缩行程参数的改变对减振器示功特性影响较小，选择复原行程参数中易调节的活塞复原孔直径D11、复原节流阀片缺口高度h1、复原阀弹簧预紧力Ff为优化变量，其中Ff仅影响开阀后的液压减振器性能［9］，3个待优化参数设计的变量范围如表2所示。

表2 待优化参数的变量范围

选择减振器复原行程开阀后运动速度为0.8 m／s的复原行程最大阻尼力为优化目标。优化目标的阻尼力设置为1 100 N。在仿真模型中保持其他参数不变，分别改变D11、h1和Ff的大小，待优化参数对示功特性的影响如图4所示。

图4 优化参数对示功特性的影响

从图4可知，开阀后的复原行程最大阻尼力随活塞复原孔直径、复原节流阀片缺口高度的减小而增大，随复原阀弹簧预紧力的增大而增大。参数优化路线如图5所示。

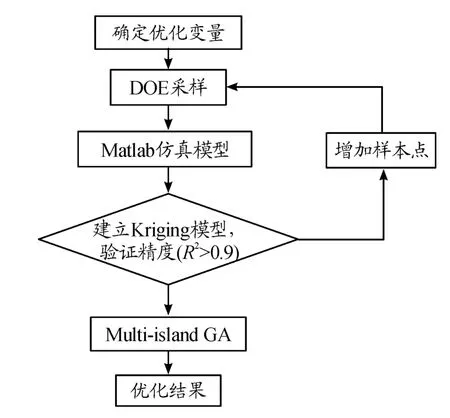
图5 减振器结构参数优化路线框图

2.1 悬架减振器结构参数Kriging模型建立

选取最优拉丁超立方的采样方式选取样本点，Kriging近似模型对初始样本训练个数的要求不得少于2n＋1个（n为输入变量个数）［10］。能够给出对未知函数的预估值，并通过对预估值的误差分析来判断其精确度；对非线性函数有着优秀的拟合效果等优点，Kriging近似模型用下式来描述输入变量与输出响应之间的关系［11］：

式中：y（x）为模型实际值；¯y（x）为模型近似值；ε（x）为实际值与近似值之间的随机误差项，其值服从标准正态分布（0，σ2）。

通过Kriging近似模型描述输入量与输出量之间的关系，最终得到优化参数和优化目标间的Kriging近似模型，如图6所示。

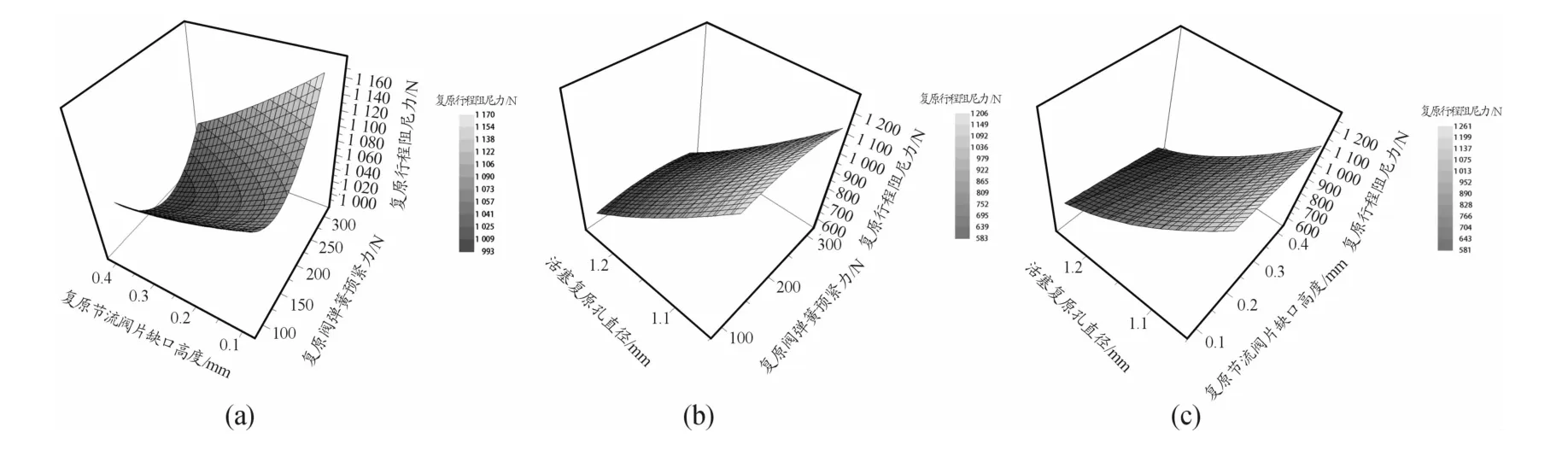
图6 优化参数与优化变量的Kriging近似模型

近似模型误差要求，预测误差用R2值表示，该值越接近于1，表明近似模型预测精度越好，要求值最小不能低于0.9［12］。图7为该近似模型拟合精度的散点图，其预测误差为0.959 7，满足精度要求，且结合图4可以看出该近似模型能很好地反映3个参数与复原行程阻尼力的关系，所以可用该近似模型代替实际模型。

图7 近似模型拟合精度的散点图

2.2 基于多岛遗传算法求最优解

多岛遗传算法源自于标准遗传算法，相较于标准遗传算法的优点在于能够有效抑制标准遗传算法中出现的早熟现象，避免遗传算法中局部最优解陷阱以及有着更高的计算效率［13］。

数目少的种群规模会使算法无法找寻到最优解而完成优化，而数目多的种群规模会使算法时间延长，降低算法的收敛速度；由多岛遗传算法的思路可知种群规模数为岛屿数与子群落数的乘积，其种群规模数取值范围是（20，200）；交叉率是指2个个体之间的交叉概率，如果交叉率设置过高，会使新基因的引入加快，导致已有的优质基因丢失，如果交叉率设置过低，会使整个群落达不到变异要求；所以交叉率的取值范围是（0.6，1.0）；变异率是少数个体存在变异的情况，保持生物多样性，变异率的取值范围是（0.01，0.05）；参数设置如表3所示。

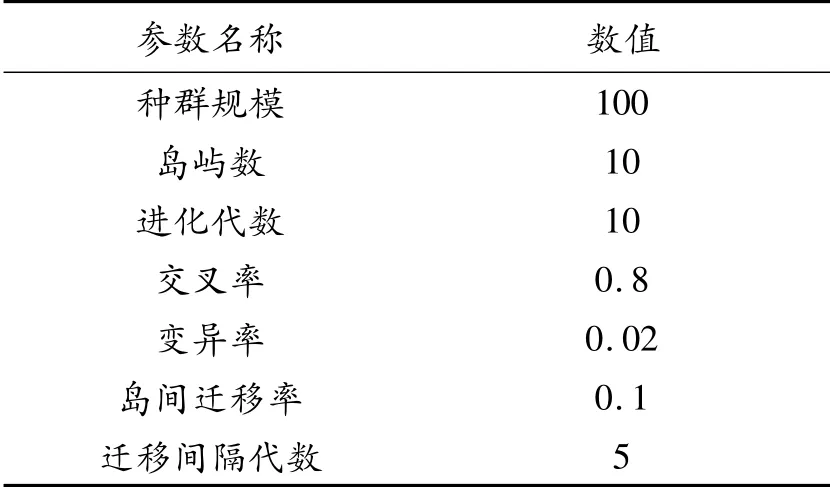
表3 多岛遗传算法参数设置

在Isight中选择多岛遗传算法后，完成多岛遗传算法参数设置后运行模型，在计算过程中该模型能够自动寻优，对各个参数进行不断的迭代直至找到最优参数，如果在寻优过程中没有找到最优参数，就需要重新调整约束条件与设计变量的范围，然后重新计算直至找到最优参数为止。经过多次调整得到参数优化结果，如表4所示。

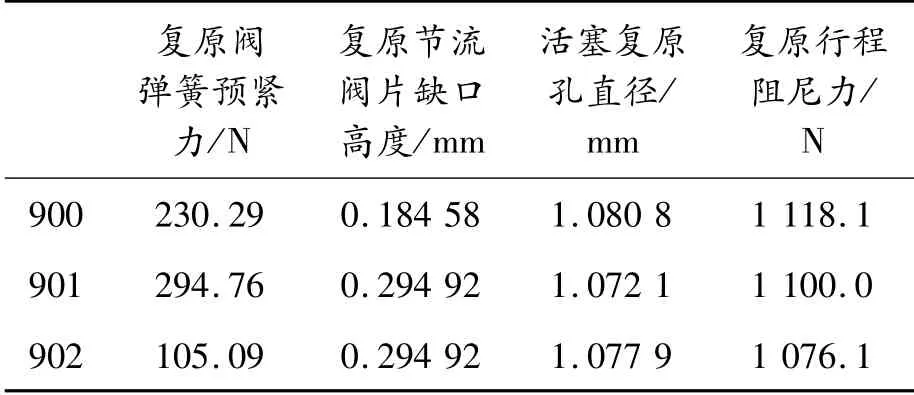
表4 参数优化结果

考虑到参数的加工精度，结合Kriging近似模型中3个参数对复原行程阻尼力的影响，优化前后的参数如表5所示。

表5 优化前后的结构参数

3 优化前后的仿真与试验验证

通过台架上的传感器采集力信号与速度信号，由台架的计算机自动绘制出该减振器优化前后的示功特性，如图8所示。仿真模型中可得到优化前后示功特性，如图9所示。

图8 优化前后的减振器台架试验示功特性

图9 优化前后的仿真示功特性

优化前后的复原行程最大阻尼力数据如表6所示。

表6 复原行程最大阻尼力 N

优化后仿真相对误差为0.446%，试验相对误差为1.82%，证明了近似模型的准确性，示功图面积增加表明该减振器的能量耗散性能得到提高。

4 结论

根据液压筒式减振器的工作原理结合流体力学理论知识，在Matlab中建立数学模型，并通过试验验证了所建立模型的准确性。与Isight进行联合仿真得到了精度较高的Kriging近似模型，利用多岛遗传算法完成了对该款减振器的3个参数的优化并进行了仿真与试验的验证。

通过优化前后仿真与试验的相对误差分别为0.446%和1.82%可以看出，建立的Kriging近似模型具有较高的精度，可以顺利代替复原－压缩行程数学模型进行优化，优化后的减振器的示功特性图面积增大，带来了更好的能量耗散性能；说明通过Isight集成Matlab建立Kriging近似模型后智能寻优的方法可行度较高，为分析其他结构参数对阻尼力的影响及对这些参数优化提供了一种新的方法。

下一步研究中，将通过最佳阻尼比与示功特性图面积之间的正比关系，选取示功图面积为优化目标，从而获得更好的优化参数值。