基于包络锁相的AMCW高精度测距算法

闫佳兴，郑 霖，杨 超

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.广西无线宽带通信和信号处理重点实验室，广西 桂林 541004)

0 引言

随着5G物联网应用的广泛开展，很多应用领域对高精度位置传感的需求日益迫切[1]。例如，华为最新发布的高分辨成像雷达，大幅提升了对目标的感知能力；对驾驶员进行非接触生命体征监测，可防止由于急性健康危害引起的事故。其中最关键的部分就是雷达传感器的设计，要求该传感器具有高精度测距及高分辨率成像的功能，以满足安全驾驶的需求。

目前高精度测距及成像方法按照距离信息的提取方式可分为2大类：

第1类是测量时间的方法。例如，大带宽信号(Linearly Frequency Modulated)通过脉压后获得较窄的脉冲[2-4]，通过测量窄脉冲的时延来获得目标距离信息。由于信号携带大的带宽，使得系统具有很高的距离分辨率，且在解扩过程中产生扩频增益，使得系统的抗干扰性能变强。但是大带宽的信号不仅会带来高成本和复杂的射频前端，且在精度的进一步提高上会受到带宽的限制。

第2类是测量相位的方法。例如，干涉雷达[5-6]只使用一个频率的连续波信号，通过测量回波信号和发送信号之间的相位差来获得精确的距离信息，但是干涉雷达存在相位模糊问题，可测量范围只相当于载波波长的一半。传统的FSK雷达[7-8]使用2个频率的信号，可放大不模糊的测距窗口，通过相位信息可以计算出目标的距离信息，但是当目标与雷达相对静止时，无法估计出目标的距离。

文献[9]提出了一种毫米波调幅连续波(Amplitude Modulated Continuous Wave，AMCW)雷达，通过包络相位对载波相位进行解模糊处理，可以在15 cm的测距窗口内实现微米精度的目标距离测量。然而本文使用双边带调制(DSB)的雷达探测信号波形，接收端采用相干方式解调处理，复杂度较高，且由于该方法的鲁棒性较差，使得系统在低信噪比(SNR)情况下测距精度大幅下降。

针对低信噪比环境下AMCW测距精度明显下降的问题，提出了一种利用低频包络和锁相环(PLL)相位锁定和跟踪来探测目标距离变化的算法。由于低频包络信号具备不模糊距离长的优点，且在低信噪比环境下经过PLL处理可有效减小系统的测距误差。通过仿真实验和实际测试验证了该算法在低信噪比环境下的鲁棒性。

1 AMCW测距基本原理

调幅连续波的发射信号可以表示为：

sTx=sin(2πfct)sin(2πfmt)，

(1)

式中，fc为载波频率；fm为调制频率。

假定环境中有一个静止目标，通过接收端下变频处理后得到复基带信号，可以表示为：

sRx=Arejφsin(2πfmt+φm)+n(t)，

(2)

式中，Ar为接收信号的幅度；φ为载波相位；n(t)为噪声；包络信号相位可以表示为φm=fmτ，τ为目标时延，则目标的距离可以表示为：

(3)

式中，c为光速；n为整数；λc与λm分别为载波波长和包络信号波长。

通过估计出的低频包络相位来计算n的值，完成对载波相位的解模糊处理，获得目标的精确距离信息。但是，考虑到系统受到高斯白噪声的影响较大，系统的测距精度会随着SNR而变化。传统AMCW信号处理框图如图1所示。

图1 传统AMCW信号处理框图

2 基于锁相环的AMCW包络跟踪算法

目标回波信号中均包含噪声，当信噪比大于15 dB时，传统的AMCW系统具有较好的测距精度；然而当信噪比降低时，将导致该系统测距的性能下降。鉴于PLL[10-14]具有窄带滤波特性与良好的跟踪特性，可对含噪声的包络信号进行捕获与跟踪，本文提出基于PLL的AMCW包络跟踪算法，可有效提升低信噪比下系统的鲁棒性。

改进后AMCW系统的发射信号可以表示为：

sTx=(A0+sin(2πfmt))sin(2πfct)，

(4)

式中，A0为直流分量。

仍然假定环境中有一个静止目标，通过接收端包络检波并去除直流分量后得到包络信号可以表示为：

srx=A1sin(2πfm(t-τ))+n(t)，

(5)

式中，A1为接收信号的幅度。

然后经过PLL处理，锁定输出的同频信号满足与接收包络相位同步，则锁定后的信号可以表示为：

sRx=sin(2πfm(nTs-τ+θ(n)))，

(6)

式中，Ts为采样时间间隔；θ(n)为PLL锁定后的稳态相差。最后跟本地的sin(2πfm(nTs))做鉴相，即可得到目标的精确距离。整个接收端信号处理框图如图2所示。

改进后系统的测距精度仅与PLL锁定后的稳态相差有关，该稳态相差可通过调节PLL参数进行约束。而PLL的性能主要由环路滤波器决定，本文采用二阶锁相环路，其数学化环路滤波器结构如图3所示。

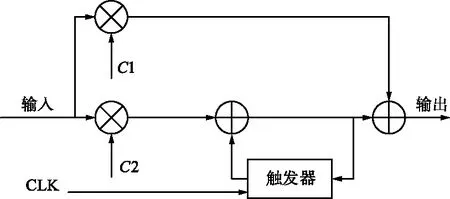
图3 环路滤波器结构

调整环路参数即是对图3中的C1，C2进行调整，文献[15]直接给出了C1，C2的计算式及其详细推导：

(7)

式中，ξ为环路阻尼系数，工程上一般取0.707；wn为环路固有振荡频率；T为频率更新周期；K为环路增益。

3 系统仿真与实测验证

结合仿真数据分别验证了在不同环境下，采用不同参数的PLL处理后可以有效发现目标，并且提高其测量精度。此外，结合自研的雷达数据采集平台采集的实测数据，验证了提出方法的有效性。

3.1 仿真测试

3.1.1 不同SNR对测距精度的影响

为验证PLL能够降低噪声的影响，提高其测量精度。该仿真实验假设环境中只有一个目标的情况下，按照表1给出的雷达系统参数验证算法的有效性，并且假设目标距离为7.5 m。

表1 雷达系统仿真参数

由于在该仿真环境中只有一个目标，PLL的固有频率可以适当减小，增加环路对输入噪声的滤除能力。计算得到环路参数C1=0.008 9，C2=0.000 000 039 5。

SNR=3 dB，目标在7.5 m处时，接收端是否经过PLL处理的多次误差比较如图4所示。从图中可以看出，经过PLL处理后，测量误差比没有经过PLL处理的低一个数量级。在不同SNR情况下，是否经过PLL处理的测距均方误差(Mean Square Error，MSE)比较如图5所示，图中每个点分别进行了500次的蒙特卡罗模拟。从图5可以看出，随着SNR的增加，测距的MSE都呈现下降趋势，但是经过PLL后，降低了包络相位检测的门限效应及噪声的影响，所以MSE比没经过PLL处理的小。因此，当环境中只有单一目标时，本方法可实现精确测距。

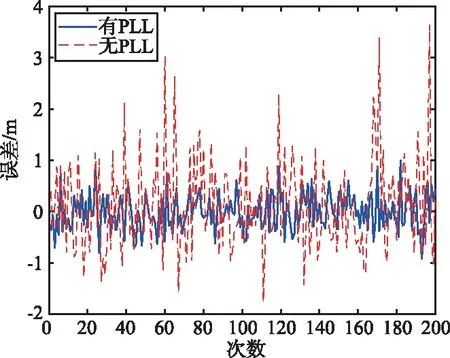
图4 有无PLL的误差对比

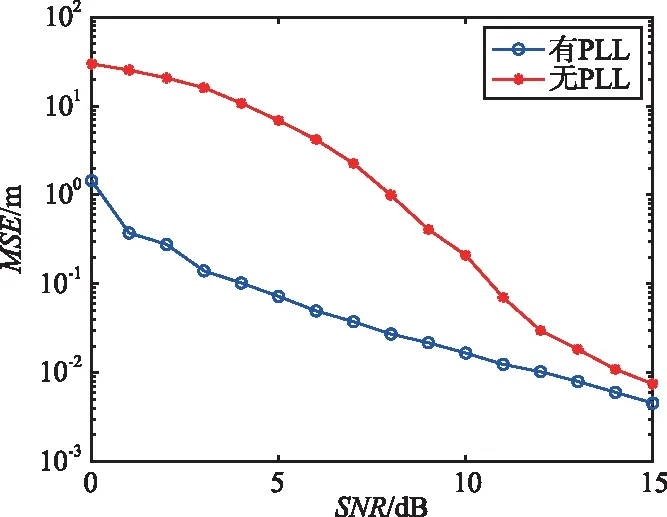
图5 不同SNR下均方误差对比

3.1.2 多径效应对测距性能的影响

该仿真实验是基于背景反射静止时的复杂环境下(也可以理解为多径情况下)，验证经过PLL处理的性能及复杂环境对其测量的影响。雷达系统参数同表1。由文献[16]可知，回波信号中由多径引起的相位误差和多径数、衰减因子有关。本仿真实验讨论的是低反射环境下对目标相位偏移量测量的影响，假定目标回波幅度大于其他反射波幅度的情况，假定目标距离为7.5 m。

不同衰减因子随SNR变化的MSE对比如图6所示。通过调节环路参数，计算得C1=0.003 6，C2=0.000 001 58。其中衰减因子代表了其他路径与目标回波的幅值比，以目标回波的幅值作为参考。从图6可以看出，衰减因子对相位误差的大小起着决定性作用。随着衰减因子的增大，多径回波信号的强度也在增大，引起的相位误差也在增大。

(a) 衰减因子为0.1

图7对比了在给定衰减因子以及SNR的情况下，随着多径数的增加带来的影响。

(a) SNR=5

从图中可以看出，经过PLL处理后，系统的鲁棒性大幅提升。图7(b)说明了随着多径数的增加，导致其相位误差增大，使得系统的测量误差变大。因此本系统在实际应用时，多径数不宜过多。

3.2 实验测试

为了验证本文方法在不同环境下的性能，利用软件无线电平台NI USRP-2974搭建了测试平台。如图8所示。

图8 实验场景1

验证平台由上位机、USRP、板状收发天线等构成，通过上位机来控制雷达波形数据的发送与接收，其中波形参数及射频参数配置与仿真相同，USRP发射功率设为0 dBm；另外，实验场景1设置在一过道中，在离设备11 m处有一静止目标。如图9所示，场景2设置在实验室中，在离设备1 m处有一人体目标，人体呼吸会造成目标的胸腔微动。

图9 实验场景2

静止目标的绝对距离估计对比如图10(a)所示，测距误差对比如图10(b)所示。从图中可以看出，在目标回波比其他径回波幅值高的情况下，经过PLL处理后的测距精度比没有PLL处理的高，且与相干处理方法相比较，测距精度几乎一致。

(a) 绝对距离测量

PLL处理后和无PLL处理的胸腔位移结果分别如图11和图12所示。

图11 PLL处理后胸腔位移结果

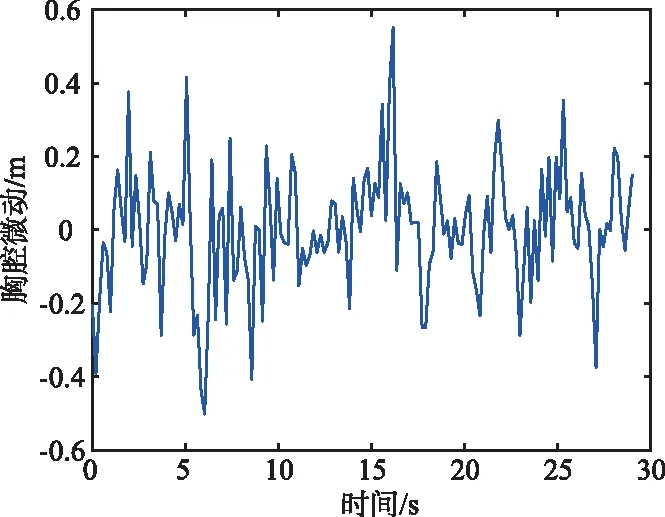
图12 无PLL处理胸腔位移结果

从图11和图12中可以看出，人体因呼吸导致的胸腔微动距离变化。经过PLL处理后系统可以较为准确地跟踪人体呼吸导致的胸腔位移变化，而没有经过PLL处理的，无法准确跟踪人体的胸腔位移变化。

正常成年人安静状态下的呼吸频率通常在0.1～0.6 Hz。PLL处理后胸腔频率估计如图13所示。

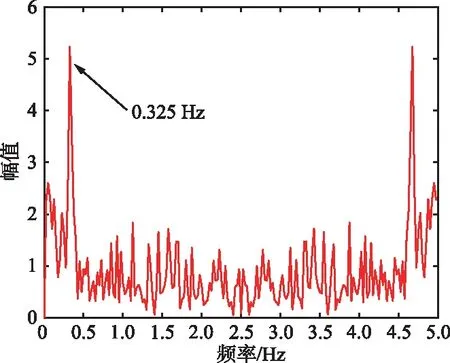
图13 PLL处理后胸腔频率估计

从图13可以看出，频谱峰值频率为0.325 Hz，经过PLL处理后估计出的人体呼吸频率在正常范围内。无PLL处理胸腔频率估计如图14所示。从图14可以看出，尽管其峰值频率也在正常范围内，但是其频谱受到噪声的影响存在很多幅值较高的频率分量，增加了系统的虚警率。

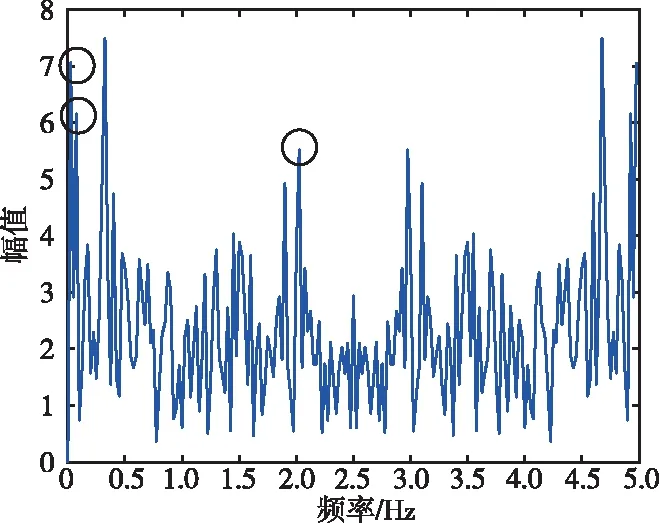
图14 无PLL处理胸腔频率估计

4 结束语

当SNR>15 dB时，传统的AMCW系统具有较好的测距精度；然而当SNR降低时，将导致系统的测距性能下降。对此，提出一种基于PLL的包络信号跟踪算法，该算法复杂度低、可移植性强，不占用大的带宽，并且PLL的引入，降低了噪声的影响，使系统的测量精度得到了提高。实验仿真与平台测试验证了该算法在不同场景下的性能优势。

在实际的复杂环境中，多径将会是影响系统测距精度的主要因素，故而下一步的研究方向为如何降低或消除多径引起的相位误差。