一种低复杂度联合过程估计干扰对消方法
2021-07-14管吉兴鲁振兴洪永彬
管吉兴,鲁振兴,张 焱,洪永彬,尹 伟
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
在连续波噪声雷达中,发射信号泄漏和杂波在时域上与目标回波无法分开,相关处理后,“旁瓣”(噪声基底)效应非常明显[1-2],会产生远距离弱目标被泄漏信号和近距离强杂波旁瓣淹没的现象,从而严重影响系统的作用距离。因此,泄漏和杂波干扰的对消是连续波噪声雷达中的一个关键环节。
干扰对消一般从射频[3-4]和数字[5-7]2个层面开展,射频对消主要用于泄漏信号抑制,对多径杂波抑制能力不足;当前,更多的研究集中于数字对消方面[8-9]。
联合过程估计算法是一种常用的干扰对消方法,利用格型预测器将参考信号转化为彼此之间相互正交的后向预测误差,然后利用多重回归滤波器将后向预测误差进行线性组合,从而实现对泄漏和杂波信号的拟合相消[10-11]。
联合过程估计虽然可以提高算法的收敛速度,但是相比于传统LMS算法,计算复杂度明显提高,不利于工程实现,尤其是当需要对消的杂波距离很远、滤波器长度很大时。在连续波噪声雷达中,参考信号可以用一个低阶的AR过程进行拟合,此时,通过理论分析可以证明,格型预测器的高阶反射系数为零。这意味着,使用一个低阶的格型预测器就可以实现对参考信号的去相关处理。基于上述分析,本文提出一种低复杂度联合过程干扰抑制方法,采用一个相对低阶的格型预测器和回归滤波器进行级联,从而大大降低算法的计算量。
1 联合过程估计对消算法
1.1 信号模型
假设强杂波存在于前M个距离单元之内,回波通道的接收信号可以表示为:
(1)
式中,Sr(n)为发射参考信号;ai为泄漏和杂波信号的复幅度;Stnc(n)则包含了目标回波、接收机噪声以及远距弱杂波,此处,假设目标位于强杂波区之外。
1.2 格型预测算法
格型预测算法结构如图1所示。其中fi(n)和bi(n),i=0,1,...,M-1,分别代表参考信号Sr(n)的前、后向预测误差,κi为反射系数。

图1 格型预测算法结构
反射系数可采用Burg算法[12]进行估计:

②i=i+1,假设采样点数为N,计算反射系数:
(2)
④ 计算第i阶前、后向预测误差fi(n)和bi(n),返回第②步,直到i=M-1。
该过程与Gram-Schmidt正交化算法等效,并且后向预测误差所包含的信息与参考信号相同[9]。所以,可以利用后向预测误差对泄漏和杂波信号进行估计。
对参考信号进行去相关之后,采用NLMS算法或者SNLMS算法的多重回归滤波器[11]对泄漏和杂波信号进行拟合相消。
2 低复杂度联合过程估计算法
2.1 参考信号的低阶AR建模
连续波噪声雷达中,发射参考信号Sr(n)为一平稳离散随机过程。根据Wood分解理论[8],Sr(n)可以由一个白噪声激励的全极点滤波器产生,也就是Sr(n)可以表示为一个适当阶数的AR过程。
在雷达实际应用中需要对消的杂波距离很远,对消器的阶数很高。如果参考信号的AR模型阶数明显低于对消滤波器的阶数,联合过程估计对消算法的运算量可以显著降低。
参考信号AR模型阶数选取的方法有很多,如最终预测误差(FPE)准则[12]、Akaike的信息论准则(AIC)[13]以及最小描述长度(MDL)准则[14]等。本文采用经典的AIC准则进行模型阶数选取(实际上,对于足够的采样点数以及较高的信噪比,几种方法得到的结果基本一致[11])。
AIC准则就是选取使下式最小的K:
(3)
假设参考信号为带宽10 MHz、采样率30 MHz的噪声调频信号,在采样点数为1 000的情况下,利用AIC准则经过100次蒙特卡罗仿真得到的平均阶数为45。通常情况下需要对消的杂波范围可达几千米,对于30 MHz的采样率而言,对消器的阶数高达几百阶。此时,参考信号的AR模型阶数明显小于对消器阶数。
2.2 低阶AR输入下的格型预测器
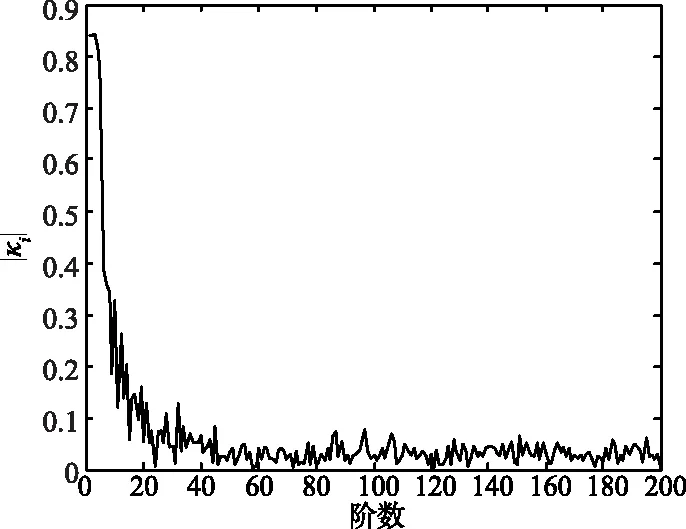
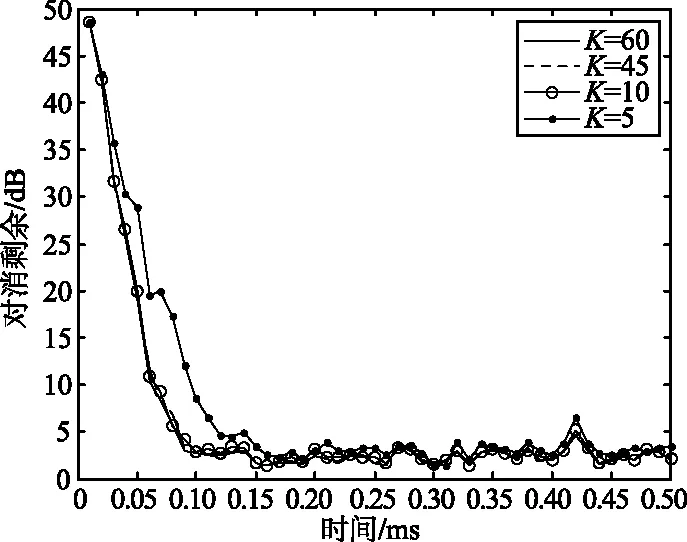
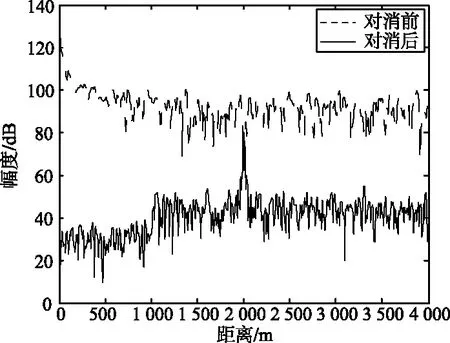
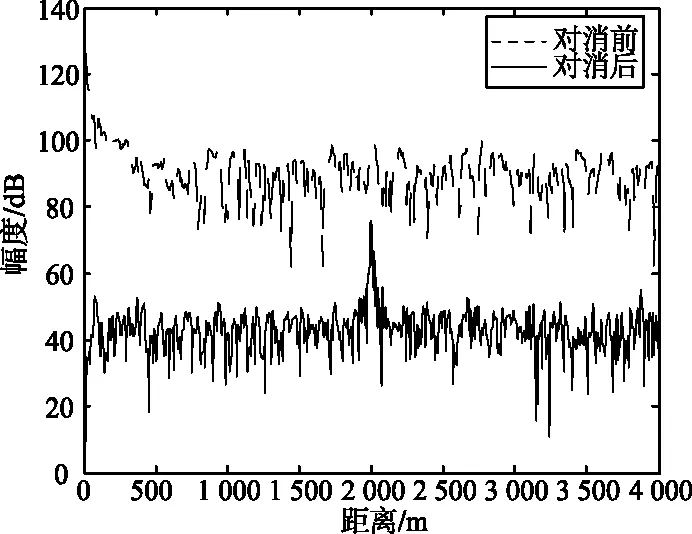
假设参考信号可以表示为一个K(K (4) 对于i>0,vr(n)与Sr(n-i)不相关,根据均方误差最小的原则可知,此时参考信号的K阶前向预测误差为vr(n)。同样对于K阶以上的前向预测器,预测误差均为vr(n)。 例如,对于K′≥K,K′阶前向预测误差可以表示为: (5) 由式(5)可知,E[|v′r(n)|2]≥E[|vr(n)|2]。因为K阶前向预测误差功率大于等于K′阶前向预测误差功率,所以E[|v′r(n)|2]=E[|vr(n)|2]。于是,有: 所以v′r(n)=vr(n)。 (6) 由于bi(n-1)为Sr(n-1),Sr(n-2),...,Sr(n-i-1)的线性组合,所以bi(n-1)与vr(n)不相关,于是Δi=0。 因为κi=-Δi-1/Pi-1,所以对于i>K,反射系数κi=0。由式(2)可知,对于i>K,有bi(n)=bi-1(n-1)。于是,在图1所示的格型预测器中,只需要计算前K阶后向预测误差即可。 图2给出了对于带宽10 MHz、采样率30 MHz的噪声调频信号。由Burg算法得到的反射系数随预测器阶数的变化,可以发现,对于较高的阶数,反射系数κi变得很小,参考信号可以用低阶格型预测器进行去相关处理。 图2 反射系数大小随阶数的变化 在参考信号AR模型阶数为K的情况下,联合过程估计器可以简化为图3所示的结构。 图3 低复杂度联合过程估计算法结构 该算法中,只需要计算出前K阶格型预测器的反射系数,前、后向预测误差,以及预测误差功率即可。K阶之后的预测误差功率与第K阶预测误差功率相等。此时后向预测误差向量变为: b(n)=[b0(n),b1(n),...,bK(n), bK(n-1),...,bK(n-M+K+1)]T。 (12) 由于在联合过程估计算法中,后向预测误差的计算占用了很大的运算量,所以,采用低阶格型预测器之后,运算量可以明显减小。 由于参考信号为平稳随机过程,所以格型预测器采用固定反射系数。此时,传统联合过程估计算法和改进的低复杂度算法每次迭代需要的运算量如表1所示,其中FL-SNLMS和FL-NLMS分别代表回归滤波器采用SNLMS和NLMS算法的联合过程估计器。如果只考虑乘法,对于M=400,K=45,改进的低复杂度FL-SNLMS算法的运算量可以降低44%,改进的低复杂度FL-NLMS算法的运算量可以降低35%。另外,计算反射系数所需要的运算量还可以降低89%。 表1 低复杂度算法与传统算法的运算量比较 在图3所示的结构中,如果改变格型预测器的阶数,使K=0,对消器就变成了自适应LMS滤波器。如果K=M-1,对消器就变成了传统的联合过程估计器。可以看出,低复杂度的联合过程估计算法是介于自适应LMS滤波器与传统的联合过程估计器之间的一种算法。 假设参考信号为带宽10 MHz,采样率30 MHz的噪声调频信号,需要对消的杂波范围为0~1 km,泄漏和杂波的总强度为46 dB,Stnc(n)的大小为0 dB,对消滤波器的长度为200阶。在样本数为1 000的情况下,计算得到相应的反射系数。 分别采用低复杂度联合过程估计算法和传统联合过程估计算法,得到的对消输出结果如图4所示。可以看出,改进低复杂度算法的收敛曲线和原始算法基本一致。 (a) 整体收敛曲线 因为低复杂度联合过程估计算法的结构介于自适应LMS滤波器与传统联合过程估计器之间,所以,当格型预测阶数K选择较大时,参考信号去相关程度较高,估计器的性能会更接近于传统联合过程估计器;当阶数K选择较小时,参考信号去相关程度较低,估计器的性能会更接近于自适应LMS滤波器。在下面的仿真中,将分析不同K取值下低复杂度算法的收敛特性。 在4.1节相同的仿真条件下,图5给出了不同K值下低复杂度联合过程估计算法的收敛曲线。在图5(a)和图5(b)中,对于K为60,45,10时,3条收敛曲线基本相同;当K=5时,收敛速度稍微变慢。 由图5可以看出,即使对于很低的预测器阶数,低复杂度算法依然可以表现出较好的收敛特性。所以,低复杂度联合过程估计器对K的估计误差敏感度较低。这也意味着在图3所示的低复杂度联合过程估计器中可以选用比AIC方法给出的阶数更低的K值,而不会带来很大的性能损失。 (a) 低复杂度FL-SNLMS 在上述仿真中,假设Stnc(n)只包含目标回波和接收机噪声,目标回波的信噪比为0 dB,目标的距离为2 km。图6和图7给出了在K=10的情况下,对消后得到的相关处理结果,其中相关处理片段长度为400 μs,片段的起始时刻为500 μs。 图6 低复杂度FL-SNLMS 图7 低复杂度FL-NLMS 可以看出,对消之前目标被泄漏和杂波的距离旁瓣淹没,而对消之后泄漏和杂波明显减弱,目标可以被检测。 在连续波噪声雷达中泄漏信号和近距杂波抑制过程中,联合过程估计对消算法通过对参考信号进行去相关处理提高了算法的收敛速度,但是也带来了运算量的明显增加。本文基于参考信号的低阶AR建模,减小了联合过程估计对消算法中格型预测器的阶数,在算法性能基本不变的情况下,降低了算法的运算量。通过数字仿真验证了算法的有效性。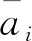
2.3 低复杂度联合过程估计算法结构

3 运算量估计

4 仿真与实测数据验证
4.1 算法的收敛特性仿真
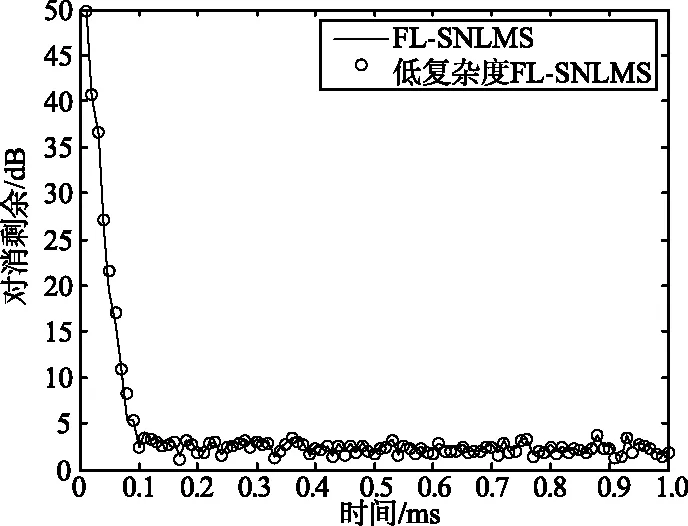
4.2 格型预测器阶数对收敛特性的影响仿真
4.3对消前后的相关处理结果分析
5 结束语
