发动机半正弦波脉冲冲击下固体火箭动力倒飞和软着陆时的位移响应
2021-07-14田红亮李森杜轩董元发张明松
田红亮,李森,杜轩,董元发,张明松
(1.三峡大学机器人与智能系统宜昌市重点实验室,443002,湖北宜昌;2.三峡大学水电机械设备设计与维护湖北省重点实验室,443002,湖北宜昌;3.三峡大学机械与动力学院,443002,湖北宜昌)
固体火箭从高空返回和垂直定点软着陆回收是火箭得以重复使用的一种重要方法。对于火箭垂直回收任务来说,回收过程既要进行减速和精确软着陆,又要满足返回过程中各种过程约束,此外还要使得燃料消耗最少。由于火箭回收的初始高度(如240 km)比较高,一般而言,整个返回弹道可以分为动力倒飞和软着陆两个阶段。
火箭回收制导算法一直是众多学者的研究方向。邵楠等针对火箭高空再入定点回收,基于凸优化方法提出了一种考虑气动力和推力控制的多阶段轨迹优化方法[1]。贺军义等使用多体系统传递矩阵法和发射动力学理论,建立了多管火箭发射动力学模型[2]。张有为等通过金属丝中空的部分向燃烧室内输出液体工质,加入负热流来改变金属丝向药柱的导热速度[3]。尹云玉对固体火箭自由运行状态获取的低频振动数据进行两次积分得到位移参数[4],还基于小波分析在时频两域皆具有表征信号局部特征的性质,对固体火箭飞行遥测过载数据进行了小波分解[5]。崔振新等建立了直升机CH-53D的动力学模型[6]。吴靖等给出了满足直升机地面共振稳定性要求的起落架刚度和阻尼的优化设计方法[7]。魏钊等考虑地球自转和发动机燃料变化所引起的附加力的影响,建立了弹性体远程火箭弹六自由度运动模型[8]。刘文芝等设计了固体火箭发动机推力矢量控制系统的结构[9]。毕祥军等提出了将线式分离系统应用在芯级与助推器的捆绑分离上[10]。Kinefuchi等应用一种计算流体动力学和有限差分时间域的耦合方法,以预测飞行高度240 km的离子化固体火箭在第三飞行阶段沿S频带遥感勘测的衰减特性[11]。Griego等通过计算流体动力学代码对固体火箭推进剂进行了灵敏度分析[12]。Gao等研究了喷射引擎燃烧室的有效燃烧[13]。Binauld等提出了获取固体燃料火箭的流量和发热的计算方法[14]。Hashim等将混合气体生成装置应用在火箭冲压喷气发动机中[15]。Fu等对二元燃料火箭发动机的实验数据进行拟合,提出了一种壁冲击模型[16]。Acharya等研究了火箭发动机再生冷通道管口的热传递机制和熵生成的特点[17]。Li等研究了火箭发动机的粉末镁和二氧化碳的燃烧特性,镁粉在干冰内继续燃烧,发出耀眼的白光,干冰易升华,干冰中的CO2之间只存在范德华力不存在氢键,一个分子周围有12个紧邻分子[18]。Du等研究了大推力火箭发动机燃烧膛的大幅度振动机制和振动控制技术[19]。
已有一些文献采用有限元方法。宏观世界规律是由微观机制所决定的,现采用理论推导的方式,在机理上进行探究。以返航时的固体火箭为研究对象,研究了动力倒飞和软着陆两个阶段的动力学响应。发动机点火之后,对固体火箭作用一个脉冲冲击力,固体火箭处于动力倒飞,在冲击脉冲持续时间之内求解出火箭的位移响应和位移绝对值的最大值;发动机熄火之后,固体火箭处于软着陆,在冲击脉冲持续时间之外推导出火箭的位移响应和位移绝对值的最大值;比较固体火箭动力倒飞和软着陆的位移绝对值的最大值的大小,取其较大值,给出位移冲击谱。
1 固体火箭的动力学响应
1.1 动力倒飞阶段(0≤t≤td)
发动机作用在火箭上的脉冲冲击力为
(1)
式中:f为脉冲冲击力的振幅;td为冲击脉冲持续时间。
当任意时间满足t≤td时,由杜阿迈尔卷积积分得固体火箭的位移响应
t≤td
(2)
式中:Tn为固体火箭振动的固有最小正周期;m′为固体火箭除燃料外的箭体质量[20]。
将式(1)代入式(2),得
t≤td
(3)
根据两正弦的积化和差公式,式(3)可变形为
(4)
式(4)简化为
(5)
固体火箭振动的固有角频率为
(6)
将式(6)代入式(5),得
(7)
式(7)进一步简化为
(8)
式中:k为固体火箭的支承刚度。
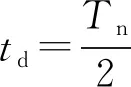
(9)
将式(8)和(9)合写在一起,得无量纲的位移响应
X(t)=
(10)
式(10)关于时间t的一阶导数为
X′(t)=
(11)
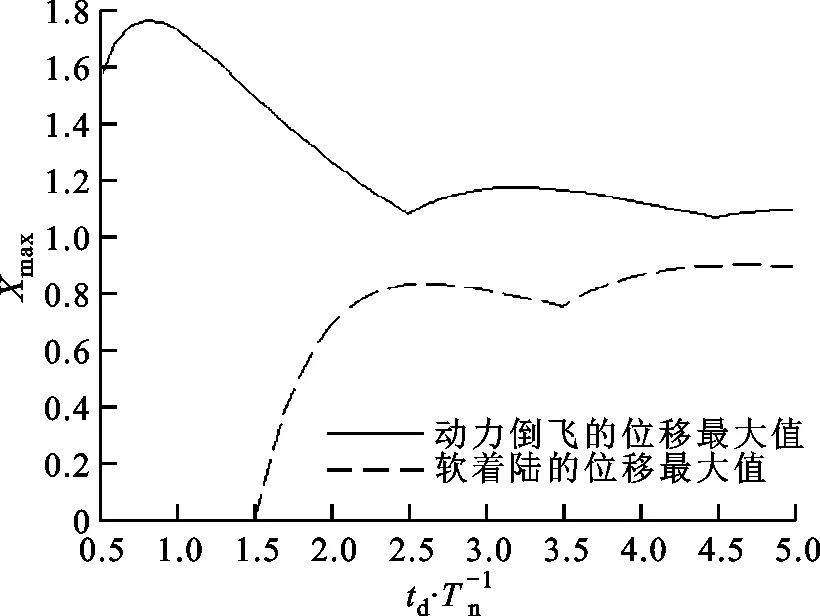
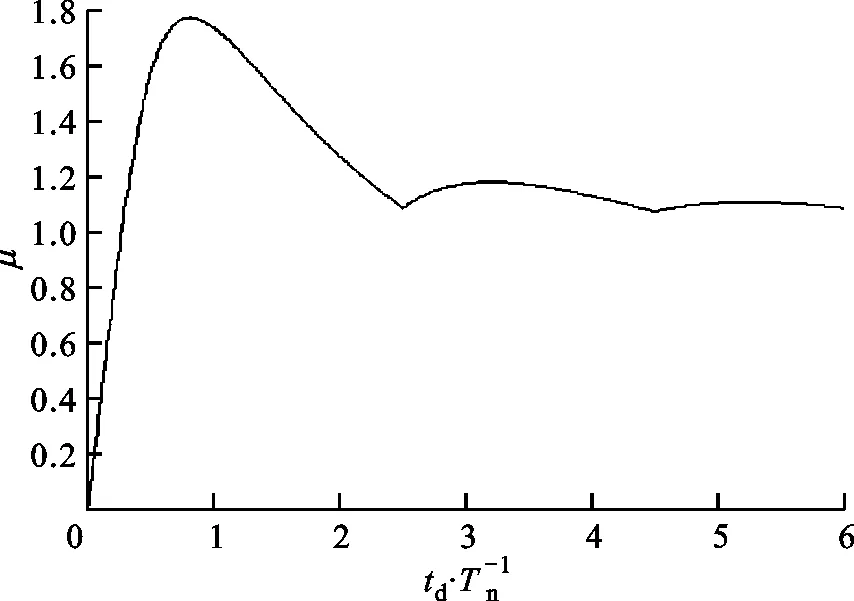
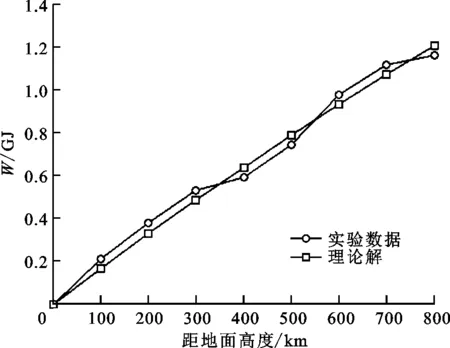
为求函数|X(t)|在闭区间0≤t≤td上的最大值,先求X(t)在开区间0 (12) 方程式(12)的第一个解为 (13) 式中:Z为整数集。 (14) (15) 式中:N*为正整数集。或者 (16) 方程(12)的第2个解为 (17) (18) 式(11)关于时间t求一阶导数,得 (19) 由式(14)和(15),将式(13)代入式(19)的第1式 (20) 故存在正数δ,函数X(t)的驻点t的一个δ邻域(t-δ,t+δ),式(13)是极小值点,式(13)中的整数用m表示,代表最小。根据式(14)和(15),将式(13)代入式(10)的第1式,得一系列极小值 (21) 按照式(18),将式(17)代入式(19)的第1式,得 (22) 故式(17)是极大值点,式中的整数用l表示,代表最大。根据式(18),将式(17)代入式(10)的第1式,得一系列极大值 (23) (a)l=1 在式(15)的条件下,选取适当的m使式(21)取得最大值 (24) 考虑到m是正整数,故取 (25) 将式(25)代入式(15),必须满足 (26) 根据取整函数[]的定义,总有 (27) 以下不等式总成立 (28) 根据式(28)和(27),不等式(26)成立。 将式(25)代入式(21),得一系列极小值式(21)的最大值 (29) 在式(18)的前提下,选择适合的l使式(23)最大 (30) 因为l为正整数,故得 (31) 将式(31)代入式(18),下式必须成立 (32) 按照取整函数[]的定义,恒有 (33) 存在以下恒不等式 (34) 根据式(34)和(33),不等式(32)成立。 将式(31)代入式(23),得一系列极大值式(23)的最大值 (35) 图2 极大值的最大值与极小值的最大值 将式(31)代入式(17),得位移最大值发生的时间为 (36) 按照式(32),式(36)中的tm Xmax=X(td)= (37) 由式(37),得位移最大值发生的时间 (38) 由式(37)和(35)可得,在闭区间t∈[0,td]上位移的最大值为 Xmax= (39) 由式(38)和(36)可得,在闭区间t∈[0,td]上位移最大值发生的无量纲时间 (40) 当任意时间满足t≥td时,由杜阿迈尔卷积积分,得固体火箭的位移响应 t≥td (41) 将式(1)代入式(41),得 t≥td (42) 根据两正弦的积化和差公式,式(42)可变形为 t≥td (43) 式(43)简化为 (44) 将式(6)代入式(44),有 (45) 式(45)进一步简化为 (46) 根据两正弦的和化积公式,式(46)可变形为 (47) (48) 由式(47)和(48)可得,无量纲的位移响应 (49) 使|X(t)|取得最大值的第1个条件为 (50) (51) 由式(51)的条件t≥td,得 (52) 使|X(t)|取得最大值的第2个条件为 (53) (54) 将式(50)代入式(49)的第1式,得位移绝对值的最大值 (55) 将式(53)代入式(49)的第2式,得位移绝对值的最大值 (56) 由式(55)和(56)可得,位移绝对值的最大值为 |X|max= (57) 值得注意的是,能将式(51)和(54)合并写成一个式子,得位移绝对值的最大值发生的无量纲时间 (58) 图3 动力倒飞和软着陆的最大位移 故火箭在整个飞行阶段的位移冲击谱为 μ= (59) (60) 对于火箭飞行的最大速度,文献[22]的结果是文献[20]的1 000倍。火箭飞行的最大速度[22]为 (61) 式中M为已燃烧燃料的质量。 长征二号F捆绑式大推力运载火箭全长为58.3 m,起飞时的质量为479.8 t,是目前我国研制的火箭中最长、最重的,起飞推力f为5.88×106N,火箭的支承刚度k为1 435 900 N/m,在太空遨游21 h,绕地球14圈,飞行约61×107m。 极大值和极小值统称为极值。从图4d、4f、4g和4h可见,函数X(t)有多个极值,极值可能取正值也可能取负值,还可能是0,需要求出|X(t)|的最大值,而不是X(t)的最大值。如果X(t)的某个极小值是负数,某个极大值是正数,且负数与正数之和小于0,为求出|X(t)|的最大值,应该取X(t)的这个极小值的绝对值。|X(t)|的最大值也可能在区间的端点处取得。 按照图4,在动力倒飞阶段,无量纲的火箭位移响应不会恒等于0;在软着陆阶段,无量纲的火箭位移响应有可能恒等于0,表明火箭的刚度较大,具有抵抗变形的能力。在图4g中,极大值1与极大值2相等。在图4h中,极大值2大于极大值1,且递增。 火箭位移冲击谱μ与冲击脉冲持续时间的关系如图5所示,由图可见,当冲击脉冲持续时间较短时,火箭位移冲击谱发生在冲击作用结束以后的软着陆阶段;当冲击脉冲持续时间较长时,火箭位移响应最大值发生在冲击作用范围内的动力倒飞阶段。 图5 位移冲击谱与冲击脉冲持续时间的关系 (a)位移最大值发生的所有时间 燃料燃烧时的情况如图7所示,涡旋发生器撑杆材料是耐高温的透明石英窗玻璃,涡旋发生器撑杆因超声速燃烧室释放的热而发生微小形变;燃料燃烧火焰可通过燃烧室出口的观察窗看到;在通用科学实验室中测试,在风洞隧道中进行的自开发氢燃料A5火箭混合循环式发动机实验,开展了82次发动机实验,总时间大于1 600 s,在存储热量风洞隧道中,也开展了自由喷气发动机实验[23-24]。 图7 燃料燃烧时的情况 火箭飞行最大速度vmax与已燃烧燃料质量的关系如图8所示,由图可见,火箭飞行的最大速度近似与燃料燃烧的质量成正比,本文理论解较接近于实验数据。 图8 火箭最大速度与燃料燃烧质量的关系 宇宙飞船绕地球飞行速度v与距地面高度的关系如图9所示,由图可见,本文理论解与神舟五号飞船的实际飞行参数较吻合,近地飞船在几百千米的高度飞行,与地球半径6 400 km相比,完全可以说是在地面附近飞行,宇宙飞船绕地球飞行速度随离地面高度的增大而呈线性减小。 图9 飞船飞行速度与地面高度的关系 把宇宙飞船从地球表面升高到h的高空处,进入轨道,飞船克服地球万有引力所做的功W如图10所示。当宇宙飞船在几百千米的高度飞行时,克服引力所做的功几乎与飞行高度成正比,因为飞行高度远小于地球半径。 图10 飞船做功与离地球表面高度的关系 火箭在返航阶段,对于给定的冲击脉冲持续时间td,火箭位移冲击谱μ、位移最大值的发生时间T见表1[25],由表可见,本文火箭位移响应最大值的计算结果与实验数据之间的相对误差为-9%~7%,火箭位移最大值发生时间的计算结果与实验数据之间的相对误差为-6%~8%。 表1 火箭返航时冲击谱参数与冲击脉冲持续时间的关系 对延迟时间进行杜阿迈尔卷积定积分,推导了固体火箭的位移响应,所得结论如下。 (1)在动力倒飞阶段,无量纲的火箭位移响应不会恒等于0。在软着陆阶段,无量纲的火箭位移响应有可能恒等于0。 (2)当冲击脉冲持续时间较短时,火箭位移响应最大值发生在冲击作用结束以后的软着陆阶段。当冲击脉冲持续时间较长时,火箭位移响应最大值发生在冲击作用范围内的动力倒飞阶段。 (3)火箭的位移达到最大值时,对应的发生时间不是唯一的,存在多个发生时间使位移取得最大值。





1.2 软着陆阶段(t≥td)
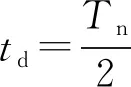

1.3 整个返航阶段(t≥0)
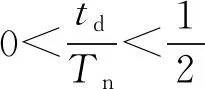

2 固体火箭返航数值仿真和讨论
2.1 整个返航阶段(t≥0)的火箭位移响应
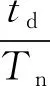








2.2 整个返航阶段的火箭位移冲击谱
2.3 整个返航阶段的位移最大值发生时间


3 实验验证




4 结 论
