基于多元回归的危化品道路运输事故风险影响因素分析
2021-07-14刘子暄
刘子暄
(北京化工大学,北京 100029)
随着我国经济的迅猛发展,现代工业化程度不断提升,使用的危化品数量和种类也越来越多,随之而来的是危化品的道路运输安全问题,一旦危化品的运输车辆在公路上出现意外,事故造成的影响范围会比较广[1]。如:2014年7月19日,在沪昆高速公路湖南邵阳范围,一辆满载乙醇的货运卡车,因司机长时间疲劳驾驶,发生与客车相撞的重大交通事故,造成54人死亡,直接经济损失达0.53亿元;2015年8月,在广东沈海高速陆丰龙山方向,一辆满载NH4NO2的货运卡车与载人客车发生追尾事故,造成6人当场死亡,30余人受伤;2016年3月,一辆满载汽油的货运罐车在京港澳高速何家垄段,因车辆故障发生爆炸事故,导致现场6人死亡。这些恶劣的交通事故给国家和群众带来巨大的经济损失和社会影响[2],所以必须有效控制危化品的运输安全。
因此如何高效辨识和分析交通事故风险是当前交通运输安全领域重要研究热点方向,潘福全、孟亚然、马昌喜,等[3]对危险化学品道路安全运输特点进行了总结归纳,并对我国目前交通安全运输相关研究现状作出了分析;高洁[4]采用综合评价的方法对危化品道路运输安全评价指标进行了构建;闫利勇[5]对危化品公路运输特点以及相应的应对措施进行了总结;吴宗之[6]针对以往危化品运输事故,以发生时间、地点等因素为出发点进行了总结;张丽[7]等对我国2006到2007年发生的危险化学品道路运输事故进行了分析和总结;辛春林[8]等对以往发生的危化品道路运输事故现场数据进行了系统分析。
Logistic回归从定义来说,属于一种广义线性回归,所以和多重线性回归分析进行对比,二者有很多的相同之处。在模型形式方面,二者具有基本相同的特点,均具有 w‘x+b,其中w和b均作为待求参数,二者的区别仅仅是在其因变量不同,其中多重线性回归的因变量是w‘x+b,即y=w‘x+b,而logistic回归则是利用函数L,将一个隐状态p与w‘x+b进行对应,即p=L(w‘x+b),然后根据1-p和p的数值大小再决定因变量的值。如果L是logistic函数,那此回归就是logistic回归,如果L是多项式函数,那此函数就是多项式回归。
基于以上内容,本文结合危化品道路运输事故影响因素及logistic回归的优势,利用危险化学品道路运输安全事故影响因素来建立数据耦合度量模型,从而将该模型下危险化学品道路运输安全事件发生的概率和风险值进行计算,为危化品道路运输安全风险预防和控制管理提供理论依据。
1 指标的选取
通过文献研究,在因果链理论的基础上,人们通过误差理论和轨迹交叉理论参照前面选取的指标对事故原因进行分析,我们可以阅读针对爆炸事故的调查报告,根据相应的专家知识,将事故的产生原因划分为以下几个方面,即:人为因素、环境因素、物质因素以及管理因素。
人为因素包括驾驶员的精神状态(是否有疲劳驾驶)、驾驶员的操作(驾驶过程中是否有不当操作)。这些因素包括危险化学品的类别、运输设备的状态和车辆的运行状态。环境因素包括时间划分、月份划分、道路类型和天气条件。管理因素包括公司资质、驾驶员资质和车辆资质。每个指标的值如表1所示。

表1 指标选取
2 相关性分析
本节运用SPSS软件通过二元相关性分析及交叉表分析,对本章构建的指标体系进行相关性分析。
2.1 二元相关性分析
在进行相关分析之前,建议使用散点图来可视化数据之间的关系。判断是否有关系(如果有*,则有关系;否则,没有关系);然后判断相关为正相关或负相关(相关系数大于0为正相关,反之亦然)。最后判断关系的亲密程度(通常相关系数大于0.4表示关系亲密)。
由表2可知,精神状态与操作失误相关性显著关系紧密。

表2 精神状态和操作失误相关性
由表3可知,运输资质与所属公司资质相关性显著关系极其紧密。

表3 运输资质与所属公司资质相关性
由表4可知,运输车辆是否合规与所属公司资质相关性显著关系极其紧密。

表4 运输车辆是否合规与所属公司资质相关性
由表5可知,运输车辆是否合规与设备状态相关性显著关系紧密。
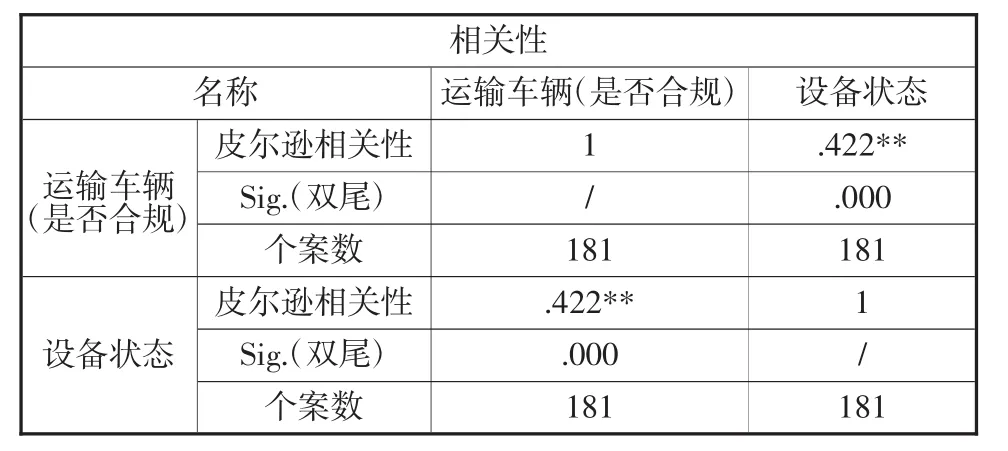
表5 运输车辆是否合规与设备状态相关性
2.2 二元logistic回归分析
2.2.1 模型系数的综合测试
模型的一行输出logistic回归模型中,所有参数是否为0的似然比检验结果。P<0.05指的是拟合模型中至少一个变量的OR值具有统计显著性,即模型具有总体显著性。
2.2.2 霍斯默-莱梅肖检验
指测试模型的拟合度。如果P值大于测试水平(即P>0.05),那么则可表明已经完全提取出当前的信息内容,并且模型拟合的优度高。
2.2.3 方程中的变量
a)本统计过程中变量的筛选方法是正向的LR法。方程表中的变量列出了最终过滤到模型中的变量及其参数。其中,sigg.a列表示模型中P值(对应变量的),Exp(B)和Exp(B)的95%CI表示模型中对应变量的OR值及其95%置信区间。
b)对于含有多类别变量的模型,在计算设置中设置“0”组作为其参考值,当测试结果是“1”组和“2”组时,计算结果分别对应于“0”组的OR值。在logistic回归中,具有虚拟变量的若干个分类变量均具备同样的In值和Out值,也就是说,相对于参照组,只要出现一组具有统计显著性变量,则与该变量相关的所有组均会被纳入计算模型中。在变量的第一行并不具有OR值,其P值指的是变量整体检验具有差异性,并存在一定的统计学意义(即至少有一组相对于参照组有统计学意义或值)。
c)本研究中的变量以“0”组为参照,因此“1”相对于“0”组的OR值和P值在第(1)行的参数中给出,而“2”相对于“0”组的OR值和P值在第(2)行的参数中给出。常数是回归方程的截距,在模型中一般没有实际意义,所以没有必要去注意它。
部分分析结果见表6~表12。
伤亡情况——品类+时间段+天气状况+事故责任(见表6~表8)。

表6 模型系数的Omnibus检验(品类+时间段+天气状况+事故责任)

表7 霍斯默-莱梅肖检验(品类+时间段+天气状况+事故责任)

表8 模型摘要(品类+时间段+天气状况+事故责任)
伤亡情况——品类+事故类型+危化品状态+事故责任方(见表9~表12)。

表9 模型系数的Omnibus检验(品类+事故类型+危化品状态+事故责任方)

表10 模型摘要(品类+事故类型+危化品状态+事故责任方)

表11 霍斯默-莱梅肖检验(品类+事故类型+危化品状态+事故责任方)
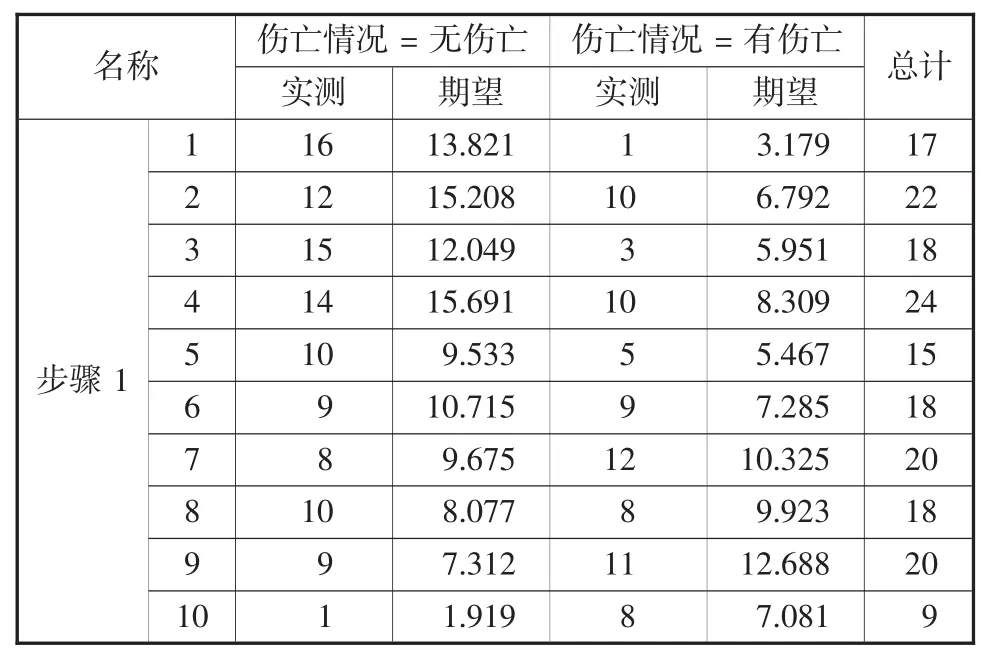
表12 霍斯默-莱梅肖检验的列联表
2.3 多元logistic回归分析
部分分析结果见表13~表22。
伤亡人数合计划分——时间段+道路类型+天气状况(见表13~表17)。

表13 模型拟合信息(伤亡人数合计划分)

表14 拟合优度(伤亡人数合计划分)

表15 分类(伤亡人数合计划分)

表16 似然比检验(伤亡人数合计划分)

表17 伪R方(伤亡人数合计划分)
伤亡人数——精神状态+运输车辆+设备状态+行驶状态(见表18~表22)。

表18 模型拟合信息(伤亡人数)

表19 拟合优度(伤亡人数)

表20 分类(伤亡人数)

表21 似然比检验(伤亡人数)

表22 伪R方(伤亡人数)
3 综合分析
由以上各因素之间的相关性分析可知,运输车辆是否合规以及司机是否具有运输资质与所属运输公司是否具有资质且合法合规运营具有极大的相关性;司机在事故发生时是否有操作失误情况与司机的精神状态有紧密相关性;危化品类型与事故后危化品状态有极为显著的相关性关系;事故类型与事故责任方有极为显著相关性;事故类型与事故后危化品状态有极为显著相关性关系;周边环境状况与事故后危化品状态有显著相关性。根据分析筛选,对于危化品道路运输事故有较大关联的因素分别为月、时间段、道路类型、品类划分、天气状况、精神状态、操作失误、危化品状态、事故类型、事故责任方。
