吕梁山特长隧道土质浅埋偏压段支护结构受力有限元模拟分析

李 鹏

（山西省交通规划勘察设计院有限公司，山西 太原 030032）

1 概述

自20世纪80年代新奥法引入国内后，在我国地下工程，特别是铁路、公路隧道设计及施工得到了迅速发展和广泛应用。但目前，我国复合式衬砌隧道的设计参数仍以工程类比法为主。虽然现行公路隧道设计规范（JTG 3370.1—2018）对各级围岩的支护结构设计参数有着明确的取值范围，但由于工程地质和水文地质情况千差万别，这种依规范取值的局限性是非常明显的。特别是对于隧道进、出口段存在偏压、浅埋、强风化、岩堆等特殊地质情况并没有具体要求。设计人员往往采用工程类比法拟定支护参数，容易出现支护参数偏弱或者过强的现象。本文采用Midas GTS NX有限元分析软件对吕梁山特长隧道进口段土质浅埋偏压段，采用工程类比法拟定支护参数的支护结构受力模拟分析，以验证拟定支护结构的安全性和经济性。

2 工程概况

吕梁山特长隧道是山西省祁县至离石高速公路的控制性工程，起点位于吕梁市文水县苍耳会寨子沟村，终点位于吕梁市离石区信义镇牛家岭村，全长9 806 m，隧道按高速公路标准设计，为分离式双洞单向行驶隧道，两洞边墙最大间距为35 m。隧道平纵线形、几何尺寸净空断面和照明标准均按80 km/h行车速度设计。全隧道设斜井2座，竖井1座。进口173 m范围内洞体围岩岩性由第四系上更新统坡洪积（Q3）粉土夹碎块石组成。洞身范围处在地下潜水位以上，围岩内一般无地下水，雨季局部可能出现短时滴渗水，围岩属于不均匀松软土。洞顶与洞壁均易产生坍塌，该段属浅埋区，易产生冒顶，稳定性差。洞顶埋深2.0～16.0 m，左右线洞口位置自然斜坡坡度约15%。

采用工程类比法拟定的支护参数为：洞口土质浅埋偏压段预留变形量12 cm，超前支护采用φ42×4 mm超前小导管，长度4.0 m，环向间距40 cm，纵向间距300 cm，系统锚杆采用φ22药卷锚杆，长度4.0 m，环向间距100 cm，纵向间距50 cm，设双层φ8钢筋网间距20 cm×20 cm，I20a钢拱架间距50 cm，C25早强喷射混凝土厚26 cm。二次衬砌采用C25钢筋混凝土厚度50 cm，配双层环向钢筋，环向钢筋直径28 mm，纵向间距20 cm，纵向钢筋直径12 mm，环向间距20 cm。

3 浅埋偏压判定

浅埋和深埋隧道的分界可按荷载等效高度值，并结合地质条件、施工方法等因素综合判定。荷载等效高度的判定可按式Hp=(2 ～2.5)hq计算。在钻爆法或浅埋暗挖法施工的条件下，Ⅳ～Ⅵ级围岩取Hp=2.5hq，荷载等效高度hq=q/γ，埋深小于或等于等效高度hq时，垂直压力视为均布，深埋隧道垂直均布压力q=γh；围岩压力计算高度h=0.45×2S-1ω；宽度影响系数ω=1+i(B-5)；隧道宽度每增减1 m时的围岩压力增减率取值0.1[1]。

依据吕梁山特长隧道设计文件，宽度B取值12.62 m，围岩级别S取值为5。计算得出本隧道浅埋分界深度Hp=31.716 m。吕梁山隧道进口段为第四系上更新统坡洪积（Q3）粉土夹碎块石组成，洞顶埋深在2.0～16.0 m，因此进口段173 m全部按照浅埋隧道计算。进口段地面横坡约15%，存在明显的偏压特点。故该隧道进口段判定为土质浅埋偏压。

4 浅埋偏压隧道围岩压力计算

a）依据公路隧道设计规范（JTG 3370.1—2018）附录偏压隧道垂直压力的计算（见图1）。

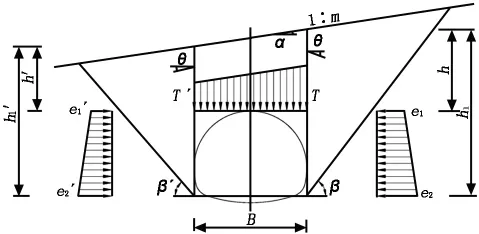
图1 浅埋偏压隧道围岩压力

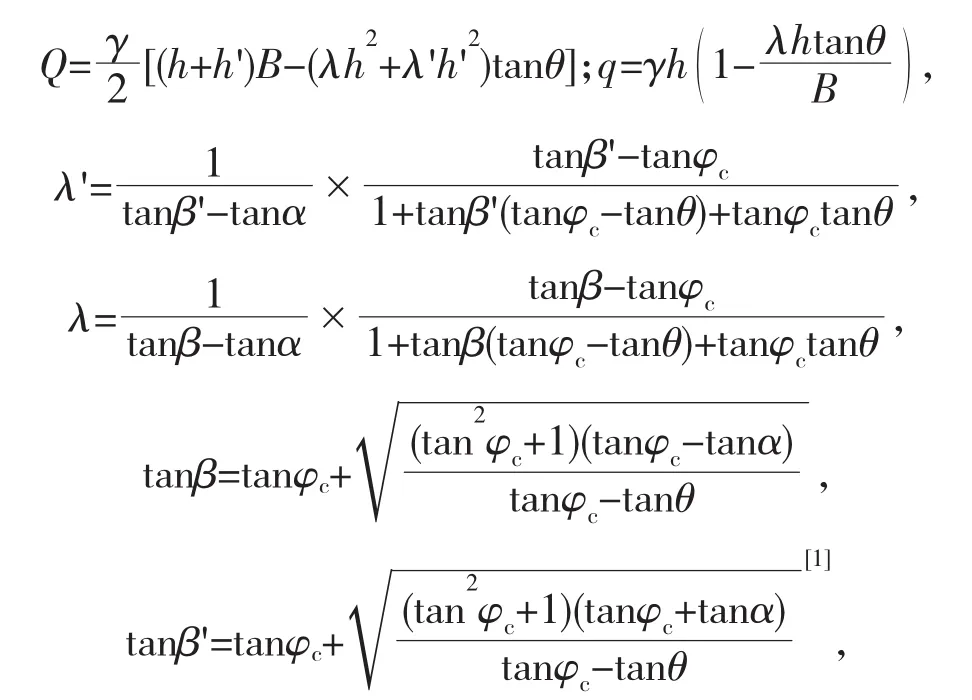
式中：h、h'分别为隧道内、外侧由拱顶水平至地面的高度，m，依据设计资料选取浅埋段埋深最大处计算，分别取值h=17.743 m、h'=15.85 m；B为隧道跨度，依据设计资料取值B=12.62 m；γ为围岩重度，取值19 kN/m3；θ为顶板岩土柱两侧摩擦角，按照公路隧道设计规范（JTG 3370.1—2018）参考表D.0.2取值，应取（0.5～0.7）φc，本文取值θ=15°；λ、λ'分别为隧道内外侧的侧压力系数；α为地面坡度，取值9°；φc为围岩计算摩擦角，取值25°；β、β'分别为内、外侧产生最大推力时的破裂角。计算可得Q=3259.29 kN/m，隧道左侧垂直压力q1=249.04 kN/m2，右侧垂直压力q2=267.49 kN/m2。

b）偏压隧道水平侧压力的计算。

依据公路隧道设计规范（JTG 3370.1—2018）隧道内侧顶点水平侧压力e1=γhλ，内侧拱脚平侧压力e2=γh1λ；外侧顶点平侧压力e1'=γh'λ'，外侧拱脚平侧压 力 e2'=γh'1λ'。 计 算 可 得 e1=184.83 kN/m2，e2=241.4 kN/m2；e1'=154.84 kN/m2，e2'=207.89 kN/m2。

5 支护结构模型建立

5.1 支护结构模型“材料、属性”的建立

土质围岩中不设系统锚杆是根据黑龙江交通厅科技项目“土质隧道中不设系统锚杆的试验研究”的成果以及黄土隧道相关研究成果。相关试验研究表明，土质围岩中锚杆施工极为困难，采用系统锚杆所花费的费用多、时间长，而效果较差；取消系统锚杆后，采取加强钢架支护、增加锁脚锚管等措施，取得了较好效果。基于以上理论，本支护结构模型不设置系统锚杆。即模型材料选择“C25混凝土各向同性”，属性采用一维梁单元模拟，具体的材料参数参照表1隧道初支材料、属性参数表。

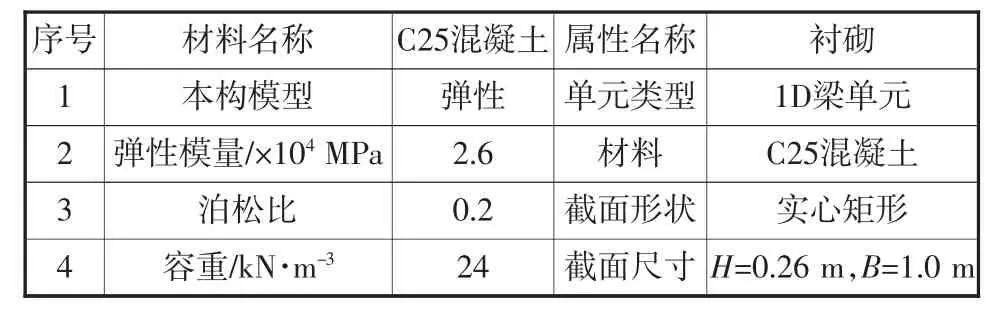
表1 隧道初支材料、属性参数表

5.2 支护结构模型“几何”的建立

结合设计文件支护结构模型采用五心圆加仰拱的隧道内轮廓型式，建立二维隧道模型。并按照“拱顶、边墙、拱脚、仰拱”依次划分网格。

5.3 支护结构模型“荷载”的建立

支护结构模型采用二维模型。采用荷载结构法建立弹性支护结构模型，即认为隧道开挖后地层的作用主要是对衬砌结构产生荷载，衬砌结构应能安全可靠地承受地层压力等荷载的作用。计算时由公式确定地层压力，然后按弹性地基上结构物的计算方法计算衬砌的内力，并进行结构截面验算。依次在支护结构模型中建立“自重”“垂直荷载”“水平荷载”。

垂直荷载即垂直土压力，分别代入前期计算值。即隧道外侧垂直压力q1=249.04 kN/m2，内侧垂直压力q2=267.49 kN/m2。水平荷载即水平土压力，分内侧、外侧分别代入前期计算值。内侧拱顶e1=184.83 kN/m2，内侧拱脚e2=241.40 kN/m2；外侧拱顶e1'=154.84 kN/m2，外侧拱脚e2'=207.89 kN/m2。

5.4 支护结构模型“边界”的建立

结构模型与土体的连接作用采用“曲面弹簧”“线单元”模拟，采用弹性连接。由于土体与隧道衬砌作用机理只能存在受压，不存在受拉的原因，支护结构模型边界确定时的曲面弹簧仅选择受压属性，去掉其受拉属性。

5.5 建立分析工况

Midas GTS NX中的曲面弹簧定性为非线性单元，因此在建立分析工况时应选定非线性静力求解。

在建立了“材料”“属性”“几何”“荷载”“边界”之后，通过静力求解，可以得到在给定受力模式下的隧道支护结构的轴力、剪力、弯矩模拟分析结果。

6 支护结构受力模拟分析结果

6.1 支护结构断面轴力分析

由图2可知，左侧边墙初支轴力最小，轴力范围为1 288～1 346 kN；右侧边墙和左侧拱顶初支轴力次之，轴力范围为1 374～1 403 kN；仰拱轴力范围在1 403～1 489 kN；而拱顶中线偏右20°范围和左、右两侧拱脚处轴力最大，轴力范围为1547～1576kN。

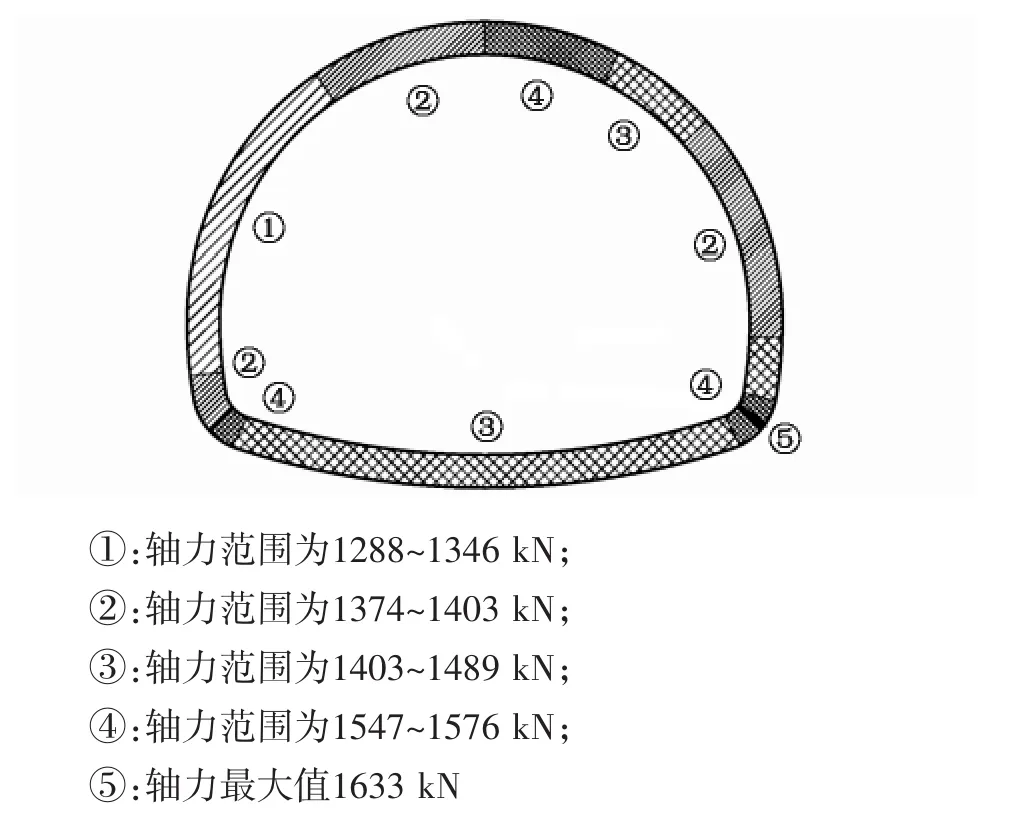
图2 支护结构断面轴力图

全断面的最大轴力出现在右侧拱脚处，轴力为1 633 kN，换算为支护结构抗压强度为：

1633 kN/（26 cm×1 m）=1633×1000 N/（0.26 m×1 m）=6280769.231 Pa=6.28 MPa。

依据公路隧道设计规范（JTG 3370.1—2018）表5.2.3，C25混凝土的轴心抗压fcd=11.9 MPa，大于结构断面轴力最大值6.28 MPa，结构断面轴力验算安全。

6.2 支护结构断面剪力分析

由图3可知，初支拱顶、仰拱中部及左侧边墙剪力最小，其剪力范围为3～179 kN；右侧边墙剪力次之，其范围为3～252 kN；而最大剪力主要集中在左右拱脚处较为宽广的范围内，左侧边墙起拱线至左侧拱脚段，剪力逐渐增大，其剪力从107 kN逐渐增大至323 kN，左侧拱脚至仰拱左侧端部段剪力区间为108～397 kN；右侧边墙起拱线至右侧拱脚段，剪力逐渐增大，其剪力从179 kN逐渐增大至397 kN，而断面最大剪力值出现在右侧拱脚至仰拱右侧端部段，其剪力值区间为180～466 kN。

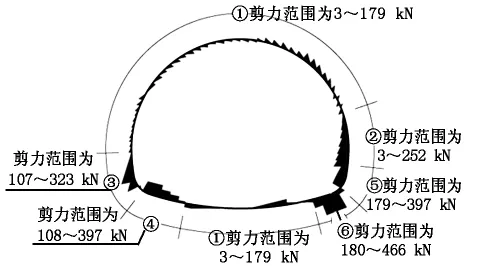
图3 支护结构断面剪力图

通过对支护结构断面剪力图分析可以得出，断面剪力最不利位置出现在左、右拱脚附近一个较大的范围内，特别是右侧拱脚偏仰拱段，较大剪力较为集中，且剪力最大值466 kN也出现在该处。

支护结构C25混凝土断面抗剪强度为：

26 cm×1 m×1.27 N/mm2=260 mm×1000 mm×1.27 N/mm2=330200 N=330.2 kN。

通过计算可知，支护结构抗剪强度为330.2 kN，小于结构断面剪力最大值466 kN。但支护结构中每延米含I20a工字钢2根，提供的抗剪能力计算值为：2×35.578 cm2×125 N/mm2=2×35.578×100 mm2×125 N/mm2=889450 N=889.45 kN，大于结构断面剪力最大值466 kN，结构断面剪力验算安全。

6.3 支护结构断面弯矩分析

由图4可知，弯矩在隧道断面上的分布较为复杂，弯矩较大值主要集中在拱顶、边墙中上部、拱脚以及仰拱端部。拱顶中心位置弯矩值为176 kN·m，由拱顶中心位置向两侧逐渐减少至3 kN·m后再逐渐增大，左侧弯矩逐渐增加至116 kN·m，右侧弯矩逐渐增加至164 kN·m。两侧弯矩之后逐渐减小，在起拱线附近达到弯矩低值6 kN·m。之后弯矩值由起拱线向拱脚处快速增大，左侧弯矩增大至371kN·m，右侧弯矩增大至419 kN·m。在左、右两侧拱脚处分别达到弯矩峰值后，弯矩值向仰拱中心方向迅速减少至极小值后再次逐渐增大，左侧增大至6 kN·m，右侧增大至115 kN·m。之后在仰拱中心处再次达到弯矩相对低点。综合隧道断面弯矩分布可以得出，断面最大弯矩值为右侧拱脚处弯矩值419 kN·m。

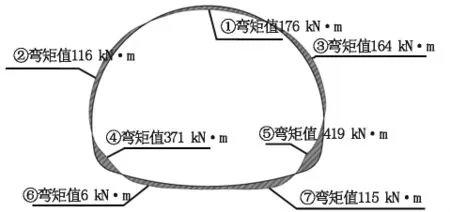
图4 支护结构断面弯矩图

a）隧道初期支护弯矩计算。

以右侧拱脚弯矩值419 kN·m计算初期支护受拉钢筋面积As。

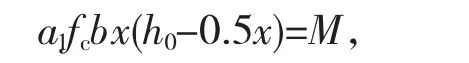
即：1.0×14.3×1000x×(260-0.5x)=419×106，求解后可得x=167 mm。

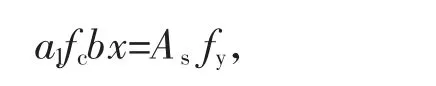
即：1.0×14.3×1000×167=215As,求解后可得As=11107 mm2。隧道初期支护抗拉主要由φ8钢筋网和I20a钢拱架承担，钢筋网间距为0.2 m，钢架间距为0.5 m，综合钢筋网和钢拱架总截面积为：50.24×5+（100×11.4）×2=2531.2 mm2，远远小于所需要的截面积11 107 mm2。

b）隧道二次衬砌弯矩计算。

以右侧拱脚弯矩值419 kN·m计算二次衬砌受拉钢筋面积As。

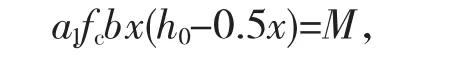
即：1.0×14.3×1000x×(450-0.5x)=419×106，求解后可得x=71 mm。

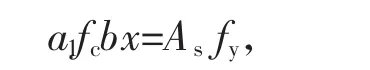
即：1.0×14.3×1000×71=360As,求解后可得As=2820 mm2。

二次衬砌钢筋混凝土配筋采用Φ28钢筋，间距20 cm，每延米换算面积为615.8 mm2×5=3079 mm2，大于所需要的截面积2 820 mm2，结构断面弯矩模拟结果验算安全。

7 结论

浅埋偏压隧道一直以来是隧道工程设计、施工的难点，目前的设计方法仍以工程类比法为主。采用工程类比法得出的支护结构参数的可靠性和经济性缺乏足够的理论依据和判定方法。本文通过Midas GTS NX有限元分析软件对吕梁山特长隧道进口段土质浅埋偏压段支护结构受力模拟分析，得出轴力、剪力以及弯矩分布图，对工程类比法拟定的支护参数进行验算，具体得出以下结论：

a）支护结构轴力模拟分析结果最大值为6.28 MPa，依据公路隧道设计规范（JTG 3370.1—2018）表5.2.3，拟定初期支护参数C25混凝土的轴心抗压fcd=11.9 MPa，大于模拟结果6.28 MPa，结构断面轴力验算安全。

b）支护结构剪力模拟分析结果最大值为446 kN，拟定初期支护C25混凝土抗剪强度为330.2 kN，小于结构断面剪力最大值466 kN。但初期支护结构中每延米含I20a工字钢2根，提供的抗剪能力值为889.45 kN，大于结构断面剪力最大值466 kN，结构断面剪力验算安全。

c）支护结构弯矩模拟分析结果最大值为419 kN·m，以此计算厚度为26 cm的初期支护所需抗拉钢筋截面积为11 107 mm2，而初支中φ8钢筋网和I20a钢拱架换算抗拉钢筋面积仅为2 531.2 mm2，也就是说，仅靠初支难以保证隧道结构的安全，必须依靠二次衬砌配筋来承载结构断面弯矩。以支护结构弯矩模拟分析结果最大值419 kN·m计算，拟定厚度为50 cm的二次钢筋混凝土衬砌所需抗拉钢筋截面积为2 820 mm2。二次衬砌混凝土配筋采用Φ28钢筋间距20 cm，每延米换算面积为：615.8 mm2×5=3079 mm2，大于模拟结果所需要的2 820 mm2，结构断面弯矩验算安全。

分析发现，即使是土质偏压浅埋的极端情况下，隧道初期支护在抗压和抗剪方面也是安全的。但初期支护在抗弯矩能力方面明显不足，必须依靠隧道二次衬砌配筋来抵抗支护结构弯矩。因此，在隧道设计和施工过程中应对二次衬砌配筋以及二次衬砌至掌子面距离给予足够的重视。隧道开挖随着掌子面的推进，围岩松弛变形不断积累扩大，支护结构断面弯矩特别是拱脚处弯矩值不断增大，二次衬砌配筋不足或者二衬与掌子面距离过大，都极易引发支护结构破坏，围岩失稳等事故发生。