基于自回归条件异方差(ARCH)族模型的收益率波动性分析

张 培， 王晶晶， 高显彩

(宿州学院 数学与统计学院, 安徽 宿州 234000)

自回归条件异方差(ARCH)模型是一种用来处理时间序列的模型。金融市场的波动率与风险直接挂钩，资产波动越大，风险则越大，获得更高收益的可能性也会越大，在股市中可以利用ARCH模型预测股票的波动率，以达到控制风险的目的。ARCH族模型发展时间不长，但被广泛应用于金融市场、理论命题检验、季节性分析等方面的波动性研究。Robert提出自回归条件异方差(ARCH)模型，并发展了一系列波动性模型及统计分析方法[1]；Bollerslev在此基础上提出的广义自回归条件异方差(GARCH)模型可以很好地描述金融时间序列波动的动态变化特征，捕捉其波动集聚性和条件异方差性[2]。近年来，Elyasiani通过GARCH模型对银行和保险公司收益风险的关联性进行了研究[3]；唐俊波等通过GARCH建模对上证指数收益率波动进行分析，得出上证指数收益率序列具有显著的异方差特征[4]；郭睿等对上证指数进行分析后认为上海证券市场股价的波动存在着显著的GARCH效应[5]；杨继平等利用非参数GARCH模型估计样本区间的波动率，分析了股市结构性波动产生的政策性影响因素[6]；张超利用GARCH族模型对上证指数波动性进行了比较研究，分析表明上证股票收益率具有显著的条件异方差性[7]；成城通过对比分析发现EGARCH模型的表现普遍优于GARCH模型[8]；邓琳通过ARCH检验建立GARCH模型的方法研究条件方差，结果表明人民币汇率市场多数时间段存在异方差效应[9]。

本文基于ARCH族模型，如广义自回归条件异方差模型 (GARCH)、EGARCH模型、TGARCH模型等，选取2010年1月至2018年12月上证指数的日涨幅数据对以上模型下的收益率波动效应进行逐个分析，通过比较发现EGARCH模型的拟合效果较好。

1 模型简介

1.1 ARCH模型

ARCH模型是一个研究波动率很重要的模型，该模型通过刻画因变量的方差方程来描述资产收益率的情况。两个假定条件同时存在一个ARCH(m)模型中，这两个条件如下：

其中：{εt}是一个独立同分布的随机变量序列，且满足E(εt)=0;Var(εt)=1。

1.2 GARCH模型

rt=c+α1rt-1-β1at-1

1.3 EGARCH模型

rt=c+α1rt-1-β1at-1

1.4 TARCH模型

在GARCH(1,1)的基础上引入了一个 “虚拟变量”Nt-1，相当于增加了一个条件，能更加直接地表现出价格变动对收益率波动来的冲击，这就是 TARCH模型，一般使用的是TARCH(1,1)模型：

rt=c+α1rt-1-β1at-1

2 股市波动性的实证分析

2.1 描述性分析

利用Eviews10.0软件对2010年1月至2018年12月连续9年上证指数的日涨幅数据进行处理，得到上证指数日对数收益率的时间序列数据走势图，如图1所示。

图1 上证指数日对数收益率序列图

由图1可知：上证指数的日对数收益率的数据波动有一个非常清晰的集聚表现，即每当出现一个非常大的波动时，在这个非常大的波动发生后会发生可能不止一个更大的波动；反之，当发生了一个小的波动时，在这以后也许会再显现出一个甚至多个细微的波动。

利用统计检验中的直方图统计可以求出上证指数对收益率序列的峰度、均值、标准差、中位数、偏度以及伴随概率值，如表1所示。

表1 上证指数日对数收益率描述性分析

表1显示：上证指数收益率均值大于0，为6.01×10-8，表明沪市大盘总体呈下行趋势，发展势头减缓，出现这种情况的主要原因是近年来我国经济发展迅速放缓，侧面反映了资本参与者对沪市收益率期望值下降；上证指数收益率的标准差0.013 974，上证指数的标准差相对较大，也体现沪市波动幅度相对较大，收益率起伏变化大；上证指数收益率偏度小于0，表示数据偏倚度不服从正态分布，为负偏态分布；上证指数收益率的峰度值大于3，表示上证指数收益率的分布具有集群性效应，即具有“尖峰、厚尾”的特点；上证指数收益率的JB统计量大，也证明了上证指数收益数据分布为非正态分布，此结论与偏度、峰度检验结果相一致。

2.2 GARCH模型的实证分析

结合上证指数数据利用Eviews10.0软件对GARCH模型拟合，并采用ARCH-LM检验对此模型的残差进行效应检验，结果如表2所示。

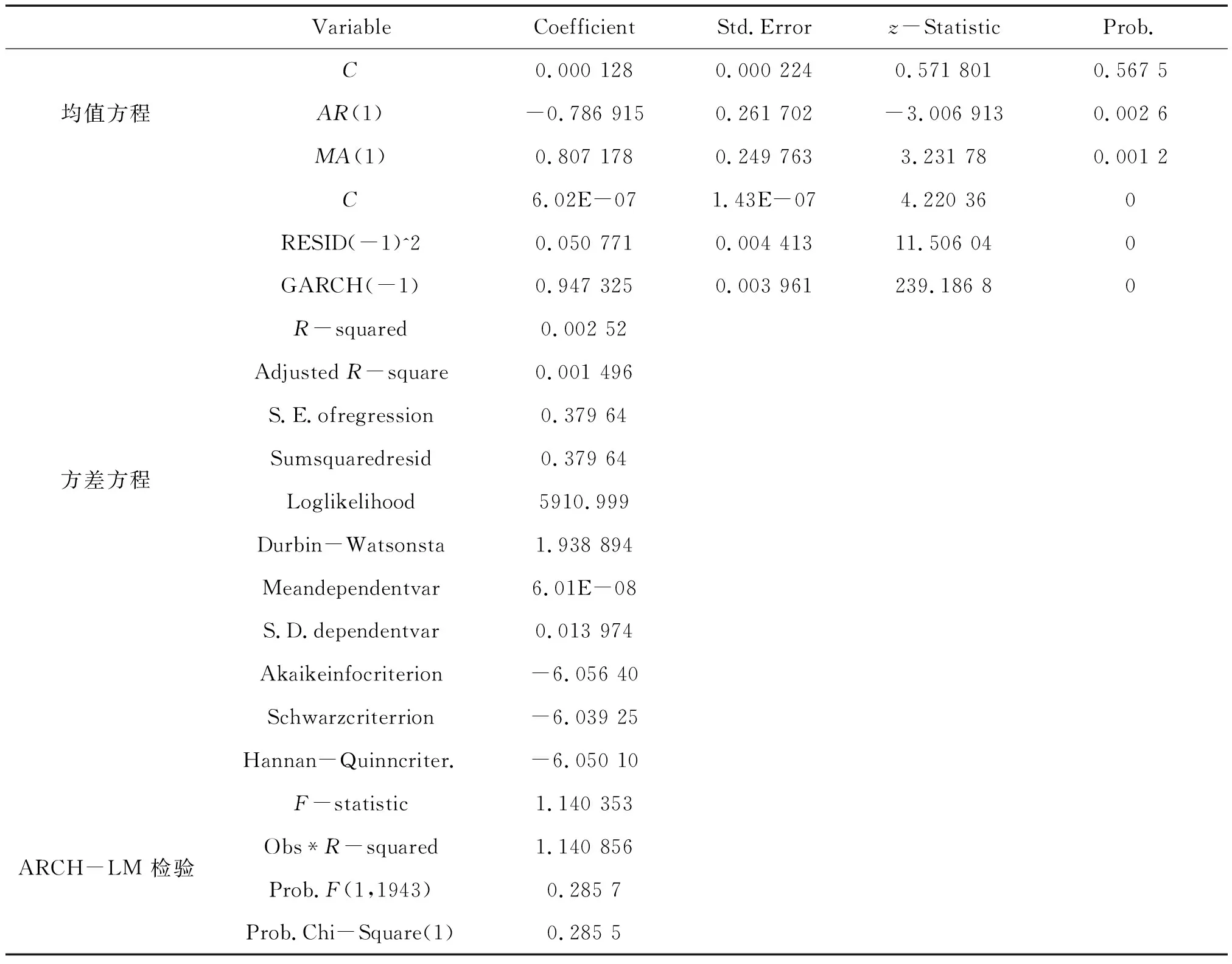
表2 上证指数GARCH的模型拟合结果

通过拟合得到GARCH模型表达式为：

rt=0.000 128-0.786 915rt-1-0.807 178at-1

从表2可以看出：各项系数均统计显著，与ARCH模型相比，对数似然值变大，AIC值和SC值变小，GARCH模型的拟合程度更佳；ARCH-LM检验过后可以发现F统计量的P值大于0.05，检验通过，原假设成立，ARCH效应不存在于建模后的残差序列中，所以GARCH(1,1)模型可以消除ARCH效应；由拟合的σ2方程可知上指收益率的波动持续系数小于1而且和1相接近，说明σ2方程满足参数的约束条件，同时条件方差对外界干扰的影响具有持续性。

2.3 EGARCH模型的实证分析

结合上证指数数据建立EGARCH模型，考察收益率波动曲线的对称性，并利用ARCH-LM检验残差是否具有ARCH效应，结果如表3所示。

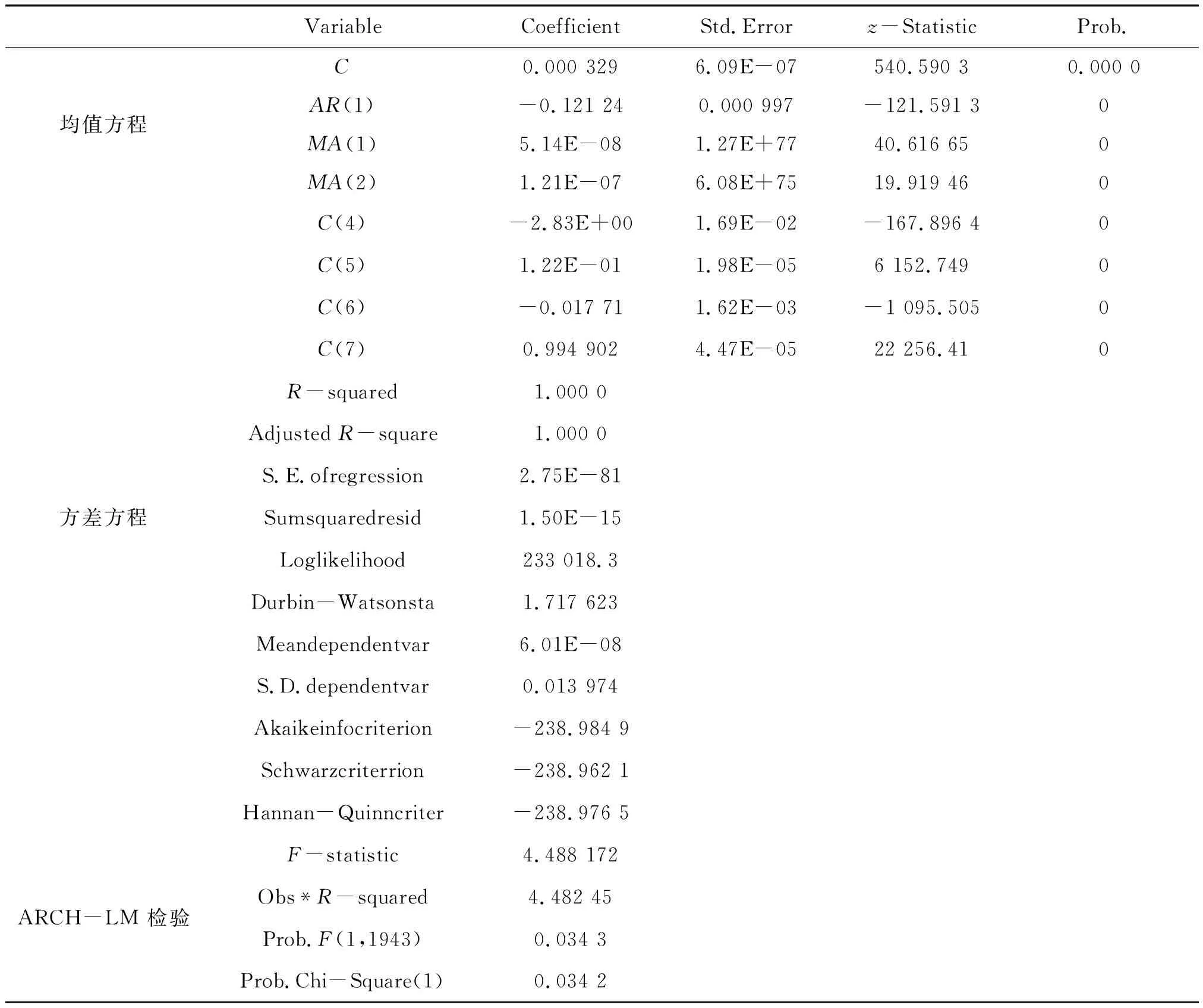
表3 上证指数EGARCH模型拟合结果

可以得到EGARCH模型的完全表达式为：

rt=0.000 329-0.121 245rt-1+5.14×10-8at-1-1.21×10-7

由表3可知：伴随概率P都为0，表示显著性是可以的，完全可以使用这个模型。在这里，模型的AIC、SC的值都为负数，而且相对而言已经是比较小的了，这表示模型具有较好的拟合效果；在上表中α=0.121 953，γ=-0.017 713<0，显著性检验不符合要求，说明上证指数收益率波动明显存在非对称性，且股市在同等条件下的负波动产生的影响大于正波动所产生的影响。

2.4 门限ARCH(TARCH)模型的实证分析

在GARCH(1,1)模型的基础上建立TARCH模型,考察价格变动对收益率波动来的影响，并对模型的残差进行ARCH-LM检验，结果如表4所示。

可以得到TARCH模型表达式为：

rt=0.000 139-0.785 832rt-1-0.806 188at-1

从表4看出：ARCH-LM检验后，F统计量的P=0.292 5>0.05，原假设成立，也就意味着 TARCH(1,1)模型可以较好地消除ARCH效应；由表4可知模型中γ=-0.003 495，它的绝对值是小于0.05的，所以收益率波动不存在对称性，也就是具有反杠杆效应，即股市在一样的条件下的负波动产生的影响大于正波动所产生的影响，这与国外股市普遍的杠杆效应相反。

表4 上证指数TARCH模型的拟合结果

3 结 语

通过自回归条件异方差(ARCH)族模型，对2010年1月至2018年12月期间沪市上证指数日收益数据做波动性分析，通过ARCH-LM检验判定AIC值和SC值的大小得知拟合效果最好的是EGARCH模型。收益数据波动性的持续性系数一直小于并接近于1，表明上证指数收益数据的波动受外界的干扰反应有一段持续性表现。同时上证指数收益数据存在很明显的不对称性，说明该数据表现出反杠杆效应，即相同情况下负的波动对股市的影响比正的波动带来的影响更大。