基于旋量理论的模块化机械臂动力学建模

吴 亮， 李宪华， 孙 青， 宋 韬,3

(1.安徽理工大学 机械工程学院， 安徽 淮南 232001； 2.上海大学 机电工程与自动化学院， 上海 200444； 3.上海机器人产业技术研究院有限公司， 上海 200063)

机器人动力学问题包括动力学正问题和动力学逆问题，正问题与机械臂的动力学仿真研究有关，逆问题则是为了实时控制的需要，利用动力学模型实现最优控制，以达到良好的动态性能和最优指标。目前，机器人动力学的研究方法有很多，较为常见的有Lagrange方法和Newton-Euler方法。Lagrange方法建模过程相对简单，系统性更强，但是计算量特别大，不适合实时计算；Newton-Euler方法则没有多余信息，计算速度快[1]。在机器人动力学建模前需要对机械臂的参数进行描述，较为常见的是D-H参数法[2]。在D-H 参数法中，各连杆相对于前一连杆建立坐标系，得到的是各个连杆相对于前一连杆的相对运动。D-H 参数法应用相对成熟，在机器人实际应用中也较为广泛。近年来，旋量法[3-5]在机器人建模方面得到了很多重视。以旋量进行机器人运动描述的最大优点是：各连杆是相对于机器人底座建立坐标系的，同时各连杆的旋量具有明确的几何意义，从而简化了机器人。王红旗等[6]基于旋量理论并利用Lagrange原理对移动机械手动力学建模。郭冰菁等[7]基于旋量理论对步态康复机器人进行了动力学的建模及仿真，验证了动力学模型的正确性。

本文基于旋量理论对6自由度模块化机械臂进行动力学建模与分析。首先，基于旋量理论建立机械臂动力学方程，通过逆动力学方程求解机械臂各关节的关节驱动力矩。然后，通过正动力学方程进行仿真，求解机械臂实际的关节位移、关节速度和关节加速度。最后，验证了机械臂动力学方程的正确性。

1 旋量理论基础

1.1 刚体运动的旋量表示

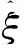
(1)

ξ=(vT，ωT)T

(2)

在旋量理论中，刚体的旋转运动可由运动旋量指数积的形式表示：

(3)

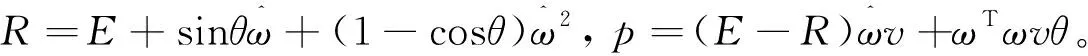
将坐标系{B}固定在刚体上，坐标系{B}相对于基坐标系{S}的位姿可以用gab表示，初始状态下的位姿为gab(0)，当刚体转动θ后的位姿为:

(4)

1.2 速度旋量与力旋量

假设与刚体相联的坐标系{B}相对于固定参考系{A}的刚体运动，其轨迹曲线为gab(t)=SE(3)，由于

(5)

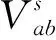
(6)

(7)

刚体运动的空间速度与物体速度之间存在如下关系：

(8)

上式将运动旋量由一个坐标系变换到另一个坐标系的矩阵称为关于g的伴随变换，记为：

(9)

刚体运动的空间速度为：

(10)

因此，对应于该运动的空间速度即为由旋量产生的速度。

伴随变换也能作用于力旋量，作用在刚体上的力旋量由纯力f和作用在一点的纯力矩τ组合而成：

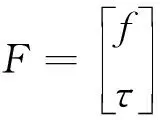
(11)

在坐标系{B}中表示的一个力旋量Fb可由一个坐标系变换到另一个坐标系{A}中，即：

(12)

2 机械臂动力学建模

本文以6自由度模块化机械臂为研究对象，该机械臂由6个转动关节串联构成，其三维模型以及简化构型如图1所示。其中：坐标系{S}为机械臂的基坐标系或惯性坐标系；坐标系{T}为机械臂的工具坐标系；ξi为各关节的运动螺旋。

图1 机械臂三维模型和坐标系

根据机械臂初始构型及建立的坐标系，可以列出各关节运动旋量的单位轴线向量ωi和轴线上的任意一点qi如表1所示。根据式(1)和式(2)即可求得初始时刻在基坐标系下表示的各关节运动旋量ξi=(vi，ωi)，再根据旋量理论求得机械臂的运动学方程。

表1 关节轴线单位向量和轴线上的点

从基座到末端执行器为各连杆设置固定在连杆的坐标系{i}，基坐标系可视为{0}。各连杆坐标系相对于基坐标系的位姿为T0,i(0)，并且坐标系在初始时刻姿态都与基坐标系相同，坐标系原点位置则与qi点重合，关节坐标系{i-1}相对于相邻的坐标系{i}的变换为：

(13)

设Φi为连杆坐标系{i}中表示的关节运动旋量，则Φi可通过伴随变换求得：

(14)

坐标系{i-1}相对于相邻的坐标系{i}和之间的变换为：

(15)

(1) 向外递归。

由于串联式机械臂连杆的特性，可以通过递归的方式从连杆1到连杆6逐次计算出机械臂各连杆的广义速度。因此，在坐标系{i}下表示的连杆i的广义速度Vi为：

(16)

式中:当i=1时，V0为基座的速度。

对式(16)进行微分可得广义加速度为：

(17)

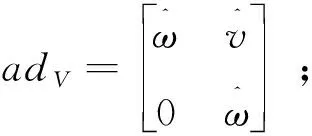
(2) 向内递归。

求得各连杆的速度和加速度后，对连杆进行受力分析如图2所示。连杆i将受到来自关节i和关节i+1的主动力，然后结合机械臂动力学参数(如表2所示)信息，可建立机械臂连杆i的Newton-Euler方程：

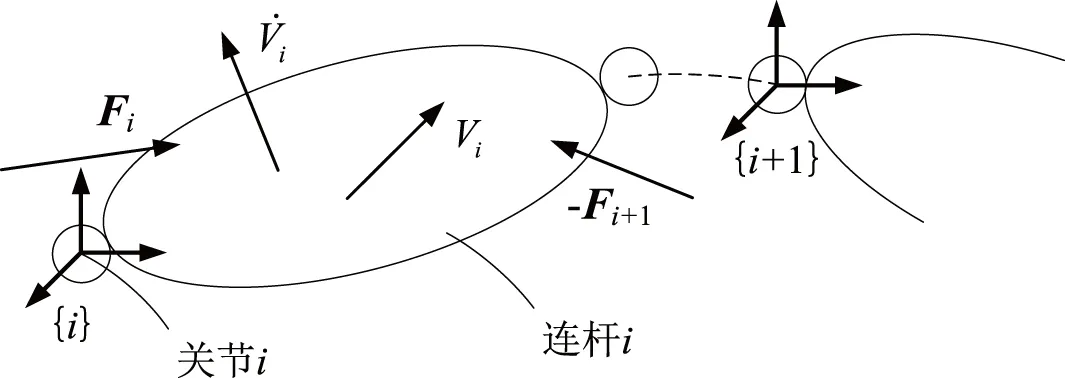
图2 机械臂连杆的受力分析

表2 机械臂的各连杆的质量参数

(18)

式中:Fi+1表示在坐标系{i+1}中，其余均表示在坐标{i}中；连杆的广义惯量Ii表示在坐标系{i}中，而惯性张量Ic表示在质心坐标系中。因此，需要变换至坐标系{i}中，可由下式求得：

(19)

(20)

式中:Ici为在连杆质心坐标系中表示的广义空间惯量；E为3×3的单位矩阵。

由式(18)可得关节i对连杆i的广义力为：

(21)

注意，当i=n时(n为关节总数)，Ti+1,i=Tn+1,n为连杆n相对于工具坐标系的位姿变换；Fi+1=Fn+1为机械臂末端所受外界接触力在工具坐标系中的表示。由于在坐标系{i}中的关节运动螺旋为Φi，所以，关节i的驱动力矩为：

(22)

通过向外递归求得各连杆的广义速度和加速度，然后通过向内递归求得关节力矩。

可以将上述递归Newton-Euler 算法表达成一个状态空间方程：

(23)

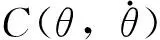
(24)

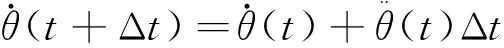
(25)

(26)

3 仿真实验

(a)(b)图3 机械臂末端执行器位置曲线图

图4 各关节力矩的变化图

(a) (b)图5 机械臂末端执行器运动轨迹对比图

图6 仿真轨迹误差图

4 结 语

基于旋量理论对6自由度模块化机械臂进行相关参数的描述，采用了递归的Newton-Euler方法求解了机械臂的逆动力学方程和正动力学方程，最后进行了动力学仿真实验，首先设定机械臂关节轨迹，然后利用逆动力学方程求出理想状态的关节力矩函数，再将关节力矩函数代入正动力学方程中进行仿真，得到关节运动轨迹，通过对比验证了本文建立的机械臂动力学模型的正确性。