基于神经网络和平直节理接触模型的细观参数标定方法1)

李新平 黄明智 王 刚 徐 坤 刘婷婷

(武汉理工大学土木工程与建筑学院，武汉430070)

基于离散单元法发展起来的颗粒流程序(particle flow code，PFC)，将岩、土等材料介质离散为抽象的颗粒单元组成的集合体，通过赋予颗粒及颗粒间接触细观参数表征类似矿物晶体及晶体结构间的黏结作用，结合颗粒间牛顿运动定律和接触间力与位移定律来模拟真实材料宏观力学特性，可以从细观角度展现裂纹孕育、扩展直至贯通的时空演化规律，在岩石力学特性数值模拟仿真中已得到大量应用[1-2]。

PFC中需定义颗粒接触的本构关系来模拟岩石宏观力学性质，在程序发展初期定义了两种接触模型：接触黏结模型和平行黏结模型，但用这两种颗粒黏结模型进行数值模拟过程中发现两者都存在着一定的缺陷，即模拟岩石材料室内试验所得出的单轴抗压强度与单轴抗拉强度之比偏低，与大多数岩石材料实际值不符[3]。为解决这一问题，许多学者从不同的角度进行了大量的改进研究，如：Cho等[4]通过改进平行黏结颗粒间接触方式而建立簇平行黏结模型；Potyondy[5]则从另一角度出发，通过改变颗粒形状研究出适用于硬质岩石的平直节理接触模型，在此接触模型下岩石材料的单轴抗压强度与单轴抗拉强度之比值得以明显增大。

在颗粒流数值模拟中，颗粒和黏结模型代表了模型材料的本构关系，其细观参数决定了数值模型的宏观力学参数，对于细观参数的标定，目前已有学者在不同的接触模型下进行了初步的研究分析。文献[6-9]以平行黏结接触模型为基础，通过数理统计方法与常用数值模拟试验探讨了颗粒材料中细观参数对宏观参数的影响关系，并尝试建立宏细观参数间的线性表达式；文献[10-11]则研究了平直节理接触模型颗粒材料中细观参数对宏观参数的影响规律及其排序结果，并根据线性回归分析得出了宏细观参数之间近似的拟合关系。

上述研究初步揭示了岩石材料宏细观参数之间复杂的映射关系，为细观参数的准确标定提供了一定参考，但研究成果中所讨论的主要力学参数偏少、未对宏观力学参数内聚力c和内摩擦角φ值进行标定,且进行验证的数值模拟与室内试验较少，拟合出的宏细观参数表达式不够准确且需多次迭代调整。基于以上研究中的不足，为了能更真实地反映出岩石的宏观力学特性，本文以平直节理接触模型为基础，通过单轴压缩、双轴压缩和直接拉伸数值模拟试验探究岩石材料宏细观参数之间的关系，进而采用善于处理复杂非线性映射关系的神经网络算法对细观参数进行标定研究，结合花岗岩室内常规试验对标定结果的准确性进行验证分析，为岩石力学数值仿真研究提供一定的参考依据。

1 PFC 2D基本理论

1.1 平直节理接触模型

平直节理接触模型与平行黏结模型、接触黏结模型最大的区别在于能够抑制颗粒黏结破坏后的旋转，如图1所示颗粒形状构造成多边形并相互“咬合”在一起，当颗粒黏结破坏后，由于颗粒之间的相互“咬合”作用，颗粒单元无法发生自由旋转运动，只能整体间滑动或脱落，与实际岩石材料内部微观构造更为接近。

图1 平直节理接触模型

平直节理接触模型有未黏结和黏结两种模式，两者的本构关系不相同。对于未黏结部分，剪切强度为

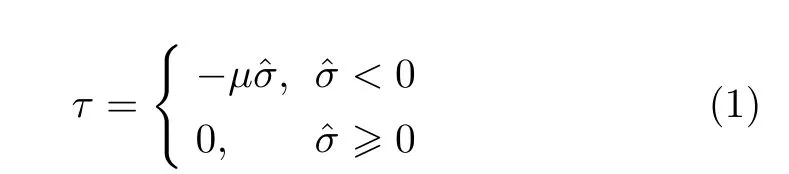
式中，µ是摩擦系数。对于黏结部分，剪切强度为

式中，c和φ分别为颗粒间黏聚力和内摩擦角。

1.2 岩石数值模拟试验

在进行PFC建模时要使模型能够较真实地反映出岩石材料的力学特性，首要考虑的就是细观参数标定，以此实现数值模型与实际岩石材料特性相匹配，细观参数标定思路就是通过对比分析岩石的数值模拟试验结果与相对应的室内试验结果。与室内试验获取试样宏观力学参数类似，在颗粒流中单轴压缩数值模拟试验(图2)也是获取颗粒材料宏观参数的常用方法，根据模拟试验结果可得到试样在平面应力状态下的单轴抗压强度σf、弹性模量E和泊松比ν等力学参数；直接拉伸数值模拟试验(图3)可直接获取模型试样的抗拉强度σt，图中黑色部分代表试样内部微裂纹分布。

图2 单轴压缩

图3 直接拉伸

除以上四个基本力学参数外，为确定岩石材料另外两个重要力学参数内聚力c和内摩擦角φ，可通过如图4所示的双轴压缩数值模拟试验(对应岩石常规三轴压缩试验)，其试验原理为：首先生成四道边界墙及离散元颗粒模型，待颗粒达到平衡后固定所有边界墙并通过伺服系统程序对模型施加围压，达到预定值后通过伺服程序不断调整左右边墙位移速度来实现施加恒定围压，最后在竖直方向上通过上下边界墙恒定的加载速率对数值试样模型施加轴向载荷，直至试样破坏为止。在不同梯度的围压下进行上述数值模拟试验，结合莫尔库仑屈服准则分析即可计算出内聚力c和内摩擦角φ的值。

图4 双轴压缩

2 颗粒流细观力学参数敏感性

为了研究颗粒流模型中细观力学参数对宏观参数的影响效果，以平直节理接触模型为研究对象，主要细观参数涉及：N，λ，kn/ks，µ，σc，cc，φ，Ec，其中：N为颗粒径向单元数；λ为颗粒最大半径与最小半径比；kn/ks为平直节理接触模型法切向刚度比；µ为接触模型摩擦系数；σc为接触模型抗拉强度；cc为接触模型黏聚力；φ为接触模型内摩擦角；Ec为接触模型有效模量[12]。由于平直节理接触模型包含的细观参数较多，如果盲目地逐个进行调试会导致大量的数值试验和繁琐的计算，可能无法建立与实际情况相匹配的数值模型，因此可先探究接触模型各细观参数对颗粒材料宏观力学参数的显著性影响，以此作为指导依据，有利于减少细观参数标定过程中的盲目性，快捷准确地建立数值模型。

2.1 正交试验设计

当遇到试验结果受多方面因素共同影响时，若采用全面试验的方法，将导致试验次数大大增加，而正交试验恰好可以解决试验次数过多的问题。正交试验设计就是通过特定模式来优化试验组合的方式来开展试验研究，利用正交表可以科学地安排各因素组合，能够在明显减少试验次数的前提下得到可靠性较强的试验结果[13-14]。

考虑到平直节理接触模型细观参数中一些非特征性参数对材料宏观特性影响较小，可根据相关研究进行简化。由文献[5,10,15-16]可知，在一定范围内，颗粒半径大小对颗粒流数值模型模拟结果的影响微乎其微，可作以下假设：平直节理接触模型中抗拉强度要小于抗剪强度，以更符合岩石实际力学特性，同时可获得与实际岩石相近的拉压强度比；按程序默认数值取λ=1，N=4；颗粒密度ρ取常用一般值2700 kg/m3；颗粒半径比Rmax/Rmin取定值1.66，且最小粒径Rmin=0.3 mm；颗粒接触模量、刚度比和摩擦系数与平直节理接触模型的相同。

除去已经确定的细观参数，剩余待标定的细观参数有6个，而进行单轴压缩、直接拉伸和双轴压缩(围压分别为5 MPa，10 MPa，15 MPa和20 MPa)数值模拟试验(模拟试样高100 mm，宽50 mm)可得到的宏观参数同样有6个，分别是：弹性模量E，泊松比ν，单轴抗压强度σf，单轴抗拉强度σt，内聚力c和内摩擦角φ。由上述细观参数在不同因素水平下建立的正交试验设计表如表1所示，其中x为因素水平，y为对应的细观参数取值，与之相对应的平直节理接触模型正交设计矩阵序列如表2所示。

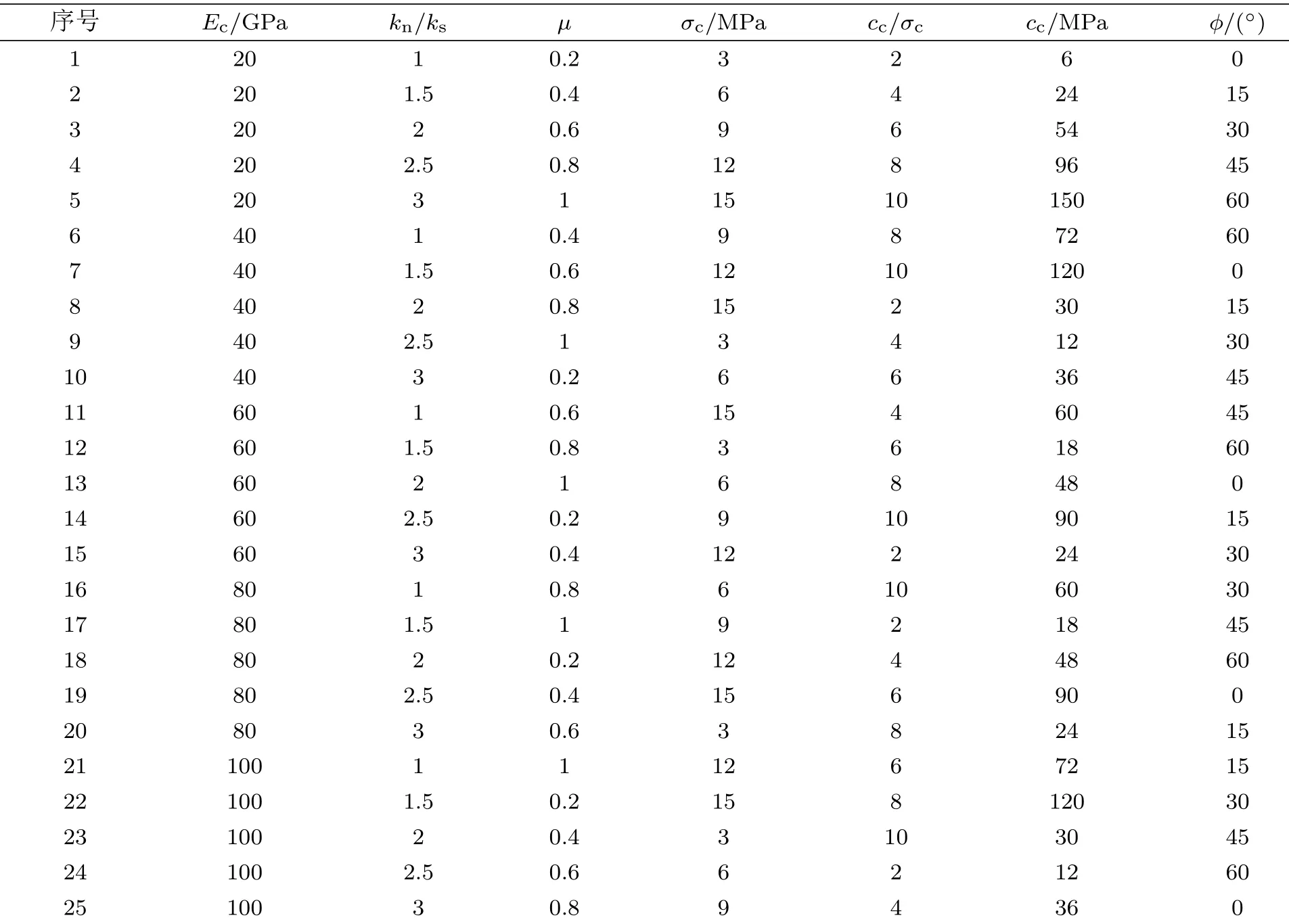
表2 平直节理接触模型正交设计矩阵序列

2.2 细观参数敏感性

当涉及到多个因素对试验结果产生影响时，可选用多因素方差法进行分析计算，基于假设检验的原理，多因素方差分析法除可判别多个因素自身是否对因变量具有显著性影响外，还可研究各因素之间共同作用对因变量产生的影响[17]，以此方法可探究多个细观参数因素及它们之间的相互作用对各宏观参数变量的显著性影响关系，进而分析细观参数的敏感性。由表2中细观参数进行数值模拟试验后，所获得的材料宏观力学参数结果如表3所示。多因素方差分析中考虑到各细观因素的主效应可取假设检验的显著性水平为α=0.05，如果相伴概率值Sig≤α，则可认为对应因素对因变量产生显著性影响，如果相伴概率值Sig>α，则无显著性影响。

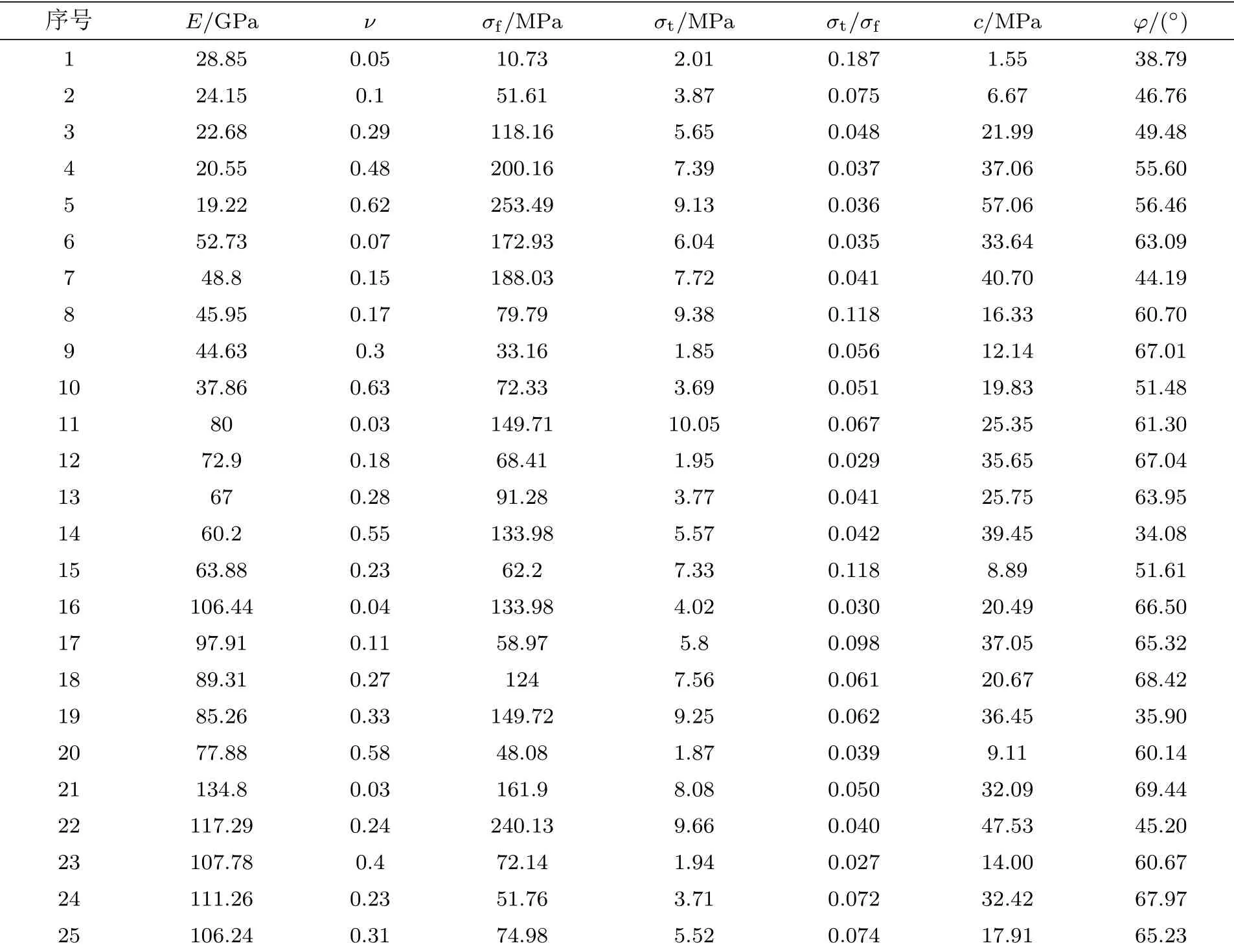
表3 正交设计矩阵序列对应的宏观参数计算结果

正交设计序列中σc，cc/σc和cc之间具有明显的线性相关性，根据宏细观参数之间的关联性程度，在多因素方差分析中选择σc，cc/σc和cc其中的一个进行分析。针对不同的宏观变量分析时选取的细观参数组合略有差异，大量数值模拟试验分析表明，宏观参数中的ν和σt/σf与cc/σc的关联性较强，所以当以这两个宏观参数为因变量进行多因素方差分析时，可选用细观参数cc/σc，而对于其他宏观参数皆采用cc进行多因素方差分析。将正交设计矩阵表2和表3中数据导入SPSS数据处理软件中，采用多因素方差法分析计算，根据多因素方差分析的F统计量和相伴概率值Sig的计算结果可知，宏观参数的显著性影响因素及各细观参数的敏感性排序结果为：E：Ec>kn/ks>µ；ν：kn/ks>cc/σc>µ>φ>σc>Ec；σf：σc>cc>φ>kn/ks>Ec；σt：σc；σt/σf：cc/σc>φ>µ>Ec；c：σc>cc>kn/ks>φ>µ；φ：µ>φ>Ec>kn/ks>cc>σc。

图5为SPSS多因素方差分析的F统计量结果及相伴概率Sig的值，根据图中结果可得以下结论：

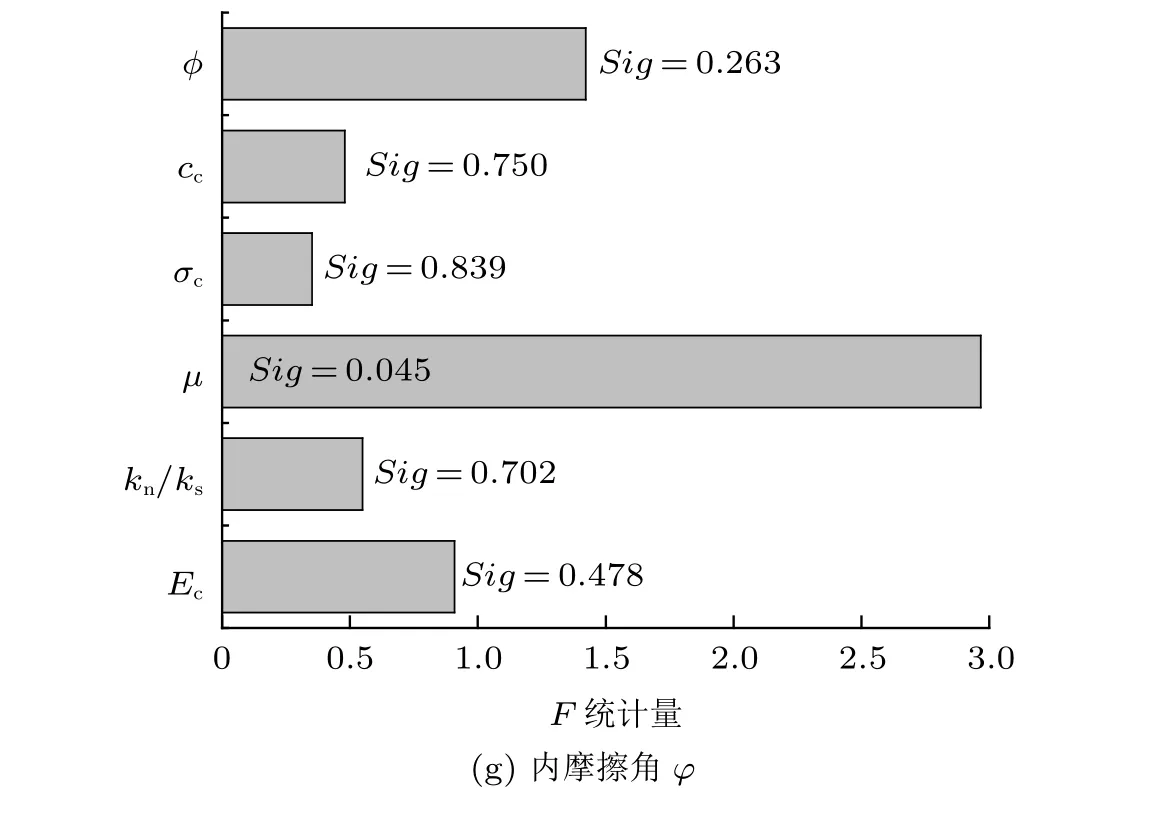
图5 多因素方差分析的F统计量及相伴概率Sig(续)

图5 多因素方差分析的F统计量及相伴概率Sig

(1)弹性模量E主要受平直节理接触模型有效模量Ec的影响，而接触模型刚度比kn/ks和摩擦系数µ对其影响很小，几乎可以忽略不计，其余细观参数对其无影响。

(2)泊松比ν基本上受所研究的细观因素共同影响，其中影响最大的因素是接触模型法切向刚度比kn/ks，接触模型的强度比cc/σc影响次之，接触模型摩擦系数µ和内摩擦角φ对其影响较小，其他细观参数对其影响可忽略不计。

(3)单轴抗压强度σf受两大主要细观因素影响，分别是接触模型抗拉强度σc和接触模型黏聚力cc，其中以σc影响更大，此外接触模型内摩擦角φ及其余细观参数对其影响很小。

(4)影响单轴抗拉强度σt的细观因素基本上只有接触模型抗拉强度σc，使其标定起来最为简单。

(5)拉压强度比σt/σf主要受接触模型的强度比cc/σc的影响，接触模型内摩擦角φ对其影响程度相对较小，其他细观参数对其影响极小。

(6)影响内聚力c的因素比较多，基本上所有细观参数都对其有影响，其中以接触模型抗拉强度σc和黏聚力cc对其影响最大，接触模型法切向刚度比kn/ks和内摩擦角φ对其影响次之，接触模型摩擦系数µ对其影响较小，其余细观参数对其影响极小。

(7)内摩擦角φ受所有细观因素共同影响，其中对其影响最大的因素是接触模型摩擦系数µ，而接触模型内摩擦角φ次之，接触模型有效模量Ec对其影响仅次于内摩擦角φ，其余3个细观参数都对其有一定的影响，但影响程度相对来说很小。

由以上分析可知，颗粒流数值模拟中各细观参数对宏观参数的影响显著性存在较大区别，宏细观参数之间具有高度非线性特征，目前大多数研究者普遍采用“试错法”进行标定[18-19],但调整过程盲目性大，费时费力。赵国彦等[7]、丛宇等[9]、陈鹏宇等[10]将数学分析与数值模拟试验相结合，根据线性回归分析拟合出宏细观参数之间的近似对应关系表达式，并以此对细观参数进行标定，但基于线性拟合法的标定过程误差较大且后期调整过程工作量繁杂，因此，亟需寻求一种更加高效、快捷的标定方法来确定细观参数。而神经网络在处理非线性映射关系方面能力突出且无需事前揭示各变量之间明确的函数关系，它具有高度非线性映射能力、极强的自学习能力和良好的自适应性，能够通过机器的自我学习和训练建立输入样本向量和输出样本向量之间的非线性预测关系，是研究已知量与未知量之间较为复杂非线性映射关系的有力工具，应用于细观参数的标定研究极具优势[20-21]。

3 细观力学参数反演及结果分析

3.1 BP神经网络原理

基于误差逆向传播而建立起的BP(back propagation)神经网络模型采用前反馈多层结构体系，其最大的优势在于不需人为的干扰，只需通过大量数据训练来自我学习和储存，便可建立样本数据对应的输入输出参数映射关系模型，且事前无需明确的数学表达式。其中自我学习机制采用梯度下降法，根据反向传播的误差值反馈来不断调整网络结构并优化模型内部权值和阈值，以达到网络模型的误差平方和最小，从而保证模型预测的准确性。原则上只要样本训练数据足够且网络模型在自我学习训练中能达到收敛条件，就可建立起输入变量与输出变量之间的映射关系模型，并以此应用于数据的预测分析，常用的BP神经网络模型拓扑结构如图6所示，主要包含以下三层结构。

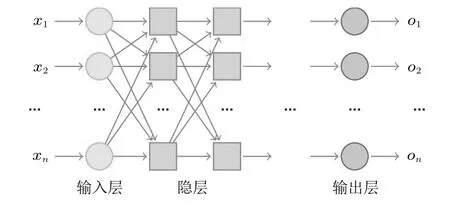
图6 前馈BP神经网络压缩结构模型

3.2 BP神经网络模型的建立与训练

基于BP神经网络分析方法，针对平直节理接触模型，建立人工神经网络细观参数反演系统。选取细观力学参数特征值：kn/ks，µ，σc，cc，φ，Ec；选取宏观力学参数特征值：E，ν，σf，σt，c，φ。由于要对细观参数进行标定，即根据岩石实际宏观力学参数反演出数值模型中相应的细观参数，可选取宏观力学参数作为输入层参数，而细观力学参数作为输出层参数，以此建立神经网络模型。参照正交设计表(25组)中细观参数的取值范围，随机生成75组细观参数并进行相应的数值模拟试验，测试出与之对应的宏观参数。选取这100组不同宏细观参数组合作为细观参数反演系统的训练样本，表4为上述宏细观参数的取值范围。由于选取的样本数据中宏细观参数都为6个，所以选取输入层和输出层神经元数目也均为6个，调试神经网络程序内部参数后导入样本数据进行训练学习，建立神经网络模型。

3.3 BP神经网络标定法可靠性验证

基于以上学习样本数据建立起BP神经网络模型，为进一步检验其可靠性，参照表4中宏观力学参数的取值范围随机生成5组宏观力学参数的测试组合样本(表5)，用来测试神经网络的预测反演能力，将其导入已经建立的网络模型预测对应的细观参数。为校核细观参数反演结果的准确性，将反演结果输入PFC中进行数值模拟，根据模拟结果计算出所需的宏观力学参数(表6)，并与导入网络模型中的宏观力学参数测试样本值进行对比分析。

表4 宏观参数和细观参数取值范围

表5 BP神经网络测试样本

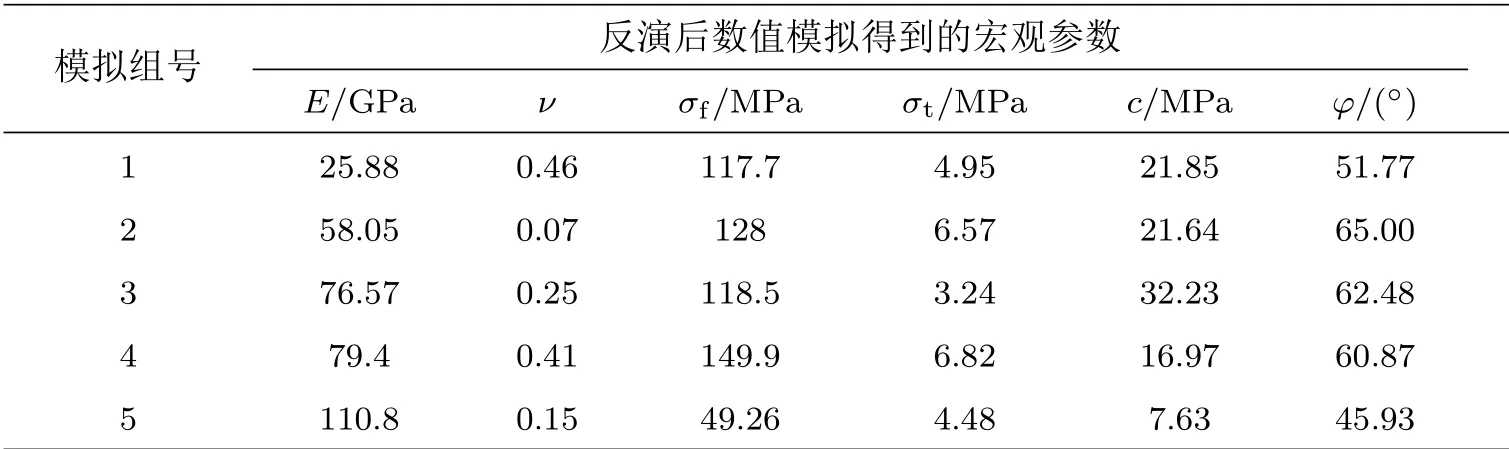
表6 细观参数反演后进行数值模拟测试出的模拟值

数值模拟测试出的宏观力学参数与随机生成的宏观力学参数测试样本进行对比分析，可验算出反演结果的精度，以此衡量反演网络系统的准确性。精度T的定义为

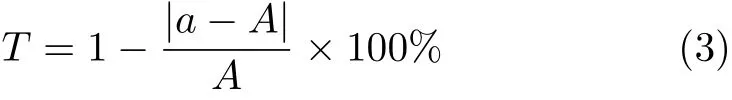
式中，a为将反演后的细观参数输入PFC中数值模拟测试出的宏观参数模拟值，A为随机生成的宏观参数测试样本值。各宏观参数的精度计算值如图7所示。

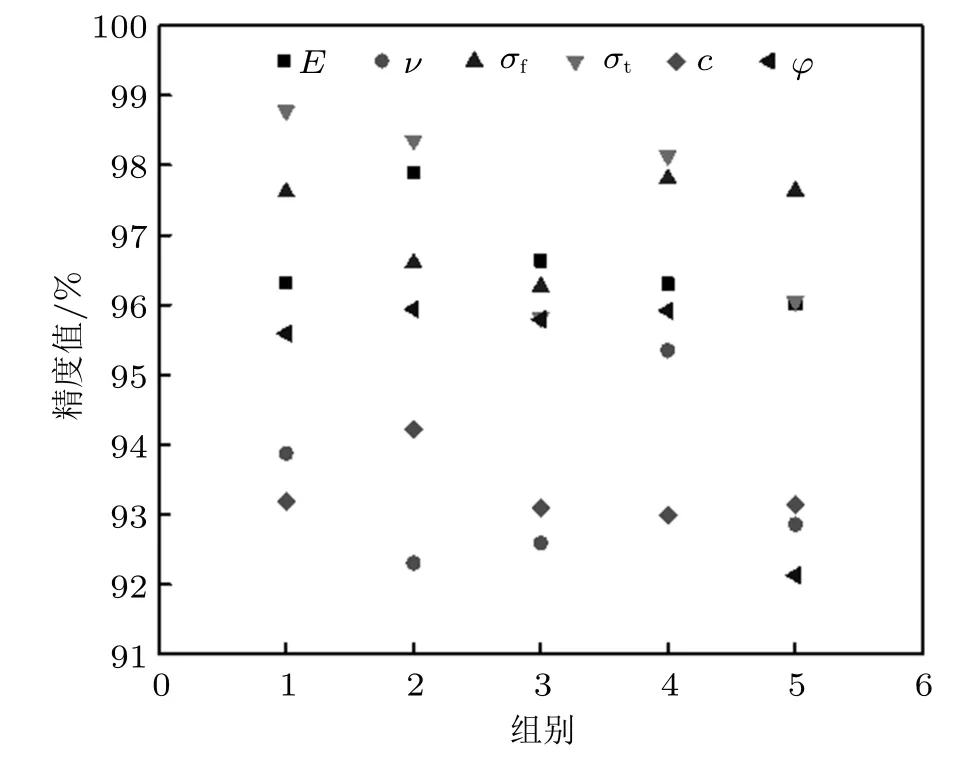
图7 测试样本各宏观参数计算精度值

根据测试样本预测结果来评价BP神经网络模型的预测反演性能，可设实际随机测试样本数据序列为µm(i)，数值模拟计算数值序列为µn(i)，其残差为

平均残差为

则残差均方差为

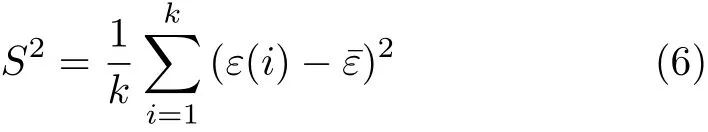
计算结果如表7所示。

由图7可知，测试样本反演结果精度普遍在90%以上，满足建模精度要求。由表7可知，测试结果平均残差值较小，说明预测误差总体比较小；残差均方差极小，表明预测结果较为稳定，建立的神经网络模型预测精度值较高且模型结构较为可靠。

表7 各宏观参数残差及均方差

3.4 BP神经网络参数反演标定细观参数

采用四川双江口水电站地下厂房爆破开挖后的斑状花岗岩，矿物成分以石英、长石居多并夹杂着黑云母和白云母等，质地较为坚硬，水工切割打磨成直径50 mm，高100 mm的标准试样，每组试样3个，在全自动化MTS(mechanical test system)试验机上进行单轴压缩、巴西劈裂和常规三轴压缩(围压分别为20 MPa，40 MPa，60 MPa和80 MPa)试验，取测试结果平均值。正交试验中数值模拟是通过直接拉伸模拟试验获得抗拉强度，而室内试验中则采用巴西劈裂试验换算出抗拉强度，两者虽略有不同，但分析正交试验模拟结果可知，直接拉伸数值模拟与巴西劈裂数值模拟测试出的抗拉强度相差较小，对细观参数标定的影响微乎其微。经数据处理后可得室内常规试验岩石力学参数的实际值，以此作为预测输入样本，导入上述建立的神经网络模型可反演出相应的细观参数，再输入PFC中进行数值模拟可测试出岩石材料宏观参数模拟值，两者对比如表8所示。

表8 岩石试样宏观力学参数的试验值和模拟值

由表8数据可以看出，数值试验模拟值与室内试验实际值非常接近，各宏观参数的模拟精度都在90%以上，说明通过实际宏观力学参数反演出的细观参数(见表9)比较准确，建立的颗粒流模型与实际岩石力学特性比较吻合，表明BP神经网络法标定平直节理接触模型细观参数是可行的。

表9 岩石颗粒试样细观参数标定结果

4 实例分析

根据表9中标定的平直节理接触模型细观参数建立起花岗岩的颗粒流数值试验模型，分别进行单轴压缩、巴西劈裂和双轴压缩等数值模拟试验，并与花岗岩对应的室内试验结果进行对比分析来检验所建立数值模型的准确性。

4.1 应力-应变曲线的对比

室内试验与数值模拟获得的单轴压缩和常规三轴压缩应力−应变曲线对比如图8所示，从图8(a)中可以看出，单轴压缩室内试验和数值模拟试验的应力−应变曲线相似度较高，弹性变形阶段直线近似平行，峰后阶段曲线近似重合且都反映出花岗岩的脆性破坏特征。初始阶段两者在曲线形态上虽略有差异，这是因为颗粒流程序建模过程中颗粒间未设置初始缺陷，应力−应变曲线在试样破坏前是一条经过原点的倾斜直线；而室内试验曲线由于天然花岗岩内初始微裂隙的存在，导致初期应力−应变呈非线性发展即压密阶段；但这并未影响两者在力学参数与破坏形式上的吻合度。由图8(b)可知，不同围压(20 MPa，40 MPa，60 MPa)下的数值模拟试验应力−应变曲线与室内常规三轴压缩应力−应变曲线契合度较高，且随着围压的增大，岩石的峰值强度增大、塑性特征增强。初始阶段数值模拟各曲线近似平行，说明不同围压对脆硬性花岗岩弹性模量影响不大，室内试验各曲线在加载初期近似重合，反映的花岗岩弹性变形特征与数值模拟结果相吻合。由此可见，基于神经网络反演出的细观参数所建立的颗粒流模型与室内试验匹配度较高，两者所得岩石的力学参数和应力−应变曲线极为接近，由于对实际复杂问题需要进行简化以方便建模，与实际情况虽存在略微差异，但大体上可以表征岩石的真实力学特性。

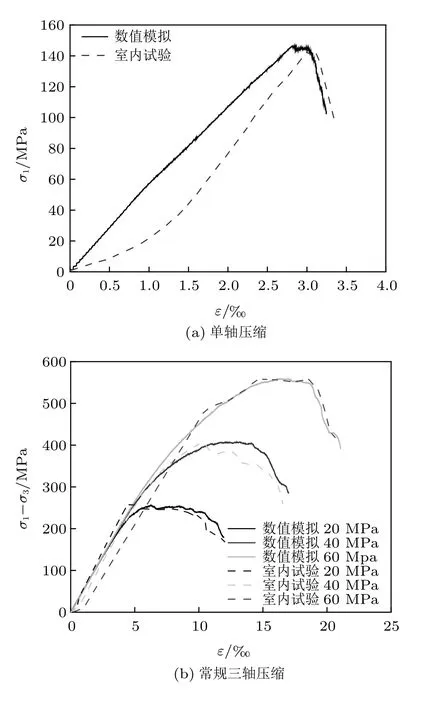
图8 应力−应变曲线对比

4.2 试样破坏形式对比

单轴压缩和巴西劈裂试样与相对应数值模型试样破坏模式对比如图9所示，可知室内试验与数值模拟岩样的破坏模式基本相同，单轴压缩下试样裂隙发展较多且较为分散，破碎较为完全，但主要表现为沿轴向的脆性劈裂破坏，局部发生轻微剪切破坏并伴随有表面层状剥落，宏观裂隙方向与最大主应力方向近似平行，破裂角大多在80°～90°之间。巴西劈裂试验下，试样首先从两端起裂，而后沿径向方向扩展直至贯通整个圆盘，最后形成一条沿径向方向的主裂缝，裂缝方向与轴向载荷加载方向基本平行；在主裂隙扩展贯通过程中，试样两端还衍生出其他次生裂隙，并沿轴向加载方向扩展，但扩展长度较小，未贯通试样。

图9 单轴压缩和巴西劈裂岩石破坏形态

常规三轴压缩试验与双轴压缩数值试验结果对比如图10和图11所示。由图10可知，20～80 MPa围压下试件以整体剪切破坏为主，形成单一宏观破裂面，在围压为20 MPa和40 MPa时，破裂面起于试样顶部，破裂角分别为72°和70°；围压为60 MPa时，破裂面从试样端部延伸，破裂角为64°；围压为80 MPa时，破裂面下移，破裂角为58°。由此可知，随着围压的增大，试样整体剪切破坏现象愈发明显，且滑移剪切带的位置也在不断发生变化，试件破裂角逐渐减小。图11中数值模拟试验试样破碎分区图(不同黑色部分代表不同破碎块体)也反映了类似规律，模型试样破坏形式基本上为宏观剪切破坏，且随围压增大，试样整体剪切破坏越明显，同时破裂角不断减小。两者对比结果说明标定的细观参数比较可靠，建立的颗粒流模型能够较真实地反映花岗岩力学特性。

图10 室内常规三轴压缩试验不同围压下岩样的破坏模式

图11 双轴数值模拟试验不同围压下岩样的破坏模式(续)

5 结论

本文基于花岗岩室内单轴、三轴压缩及巴西劈裂试验，结合离散元软件PFC2D，探究了平直节理接触模型中宏细观参数之间的影响关系，并通过多因素方差分析对细观参数敏感性进行排序，进一步运用BP神经网络法对细观参数标定进行应用研究，得出的主要结论如下：

(1)运用正交试验设计科学安排数值试验并采用多因素方差分析法探究各因素对因变量的显著性影响关系，以此研究了平直节理接触模型中宏细观参数之间的关系并对细观参数敏感性排序，结果表明各细观参数对宏观参数的影响显著性存在较大区别，宏细观参数之间的关系具有高度非线性特征。

(2)建立神经网络预测反演模型，并对平直节理接触模型中细观参数进行标定，标定结果表明岩石材料各宏观参数模拟值精度都在90%以上，且模拟值总体误差较小，神经网络预测模型反演出的细观参数较为可靠；神经网络标定法在平直节理接触模型中可作为一种高效、便捷的建模方法。

(3)以花岗岩室内单轴压缩、巴西劈裂和三轴压缩试验为基础，采用神经网络标定法建立花岗岩颗粒流模型，进行单轴压缩、巴西劈裂和双轴压缩数值模拟试验，模拟结果与室内试验结果对比表明两者获得的岩石材料宏观力学参数和应力−应变曲线基本一致，且两者试样的破坏模式极为接近，验证了所建立花岗岩颗粒流模型的准确性，即可表征岩石材料的真实力学特性。