赏析一道突出考查运动与相互作用观核心素养的创新题

湖北

(作者单位：湖北省监利市第一中学)

自八省联考以来，物理考试时间调为75分钟，湖北连续几次大型联考平均分都不理想，师生普遍觉得时间太紧，难度过大。武汉市四月联考试卷却获得了老师们的普遍好评，题目新颖但不超纲，考查主干知识和创新思维。我觉得其中有代表性的是选择题第7题。

此题具有新高考考查创新能力的特点，通过物理知识在生活情境中的应用，考查了如何灵活选取物理学规律来解决实际问题，不仅能引导学生关注主干知识的理解和运用，还能促进学生回归教材；本题考查了类比创新思维，通过对常见模型的变式拓展，考查学生在新情景中模型建构的能力，是一道考查科学思维的好题；同时，又能帮助学生归纳运动性质与受力条件的对应关系，即建立清晰的运动与相互作用观，更能培养学生的物理学科核心素养。

一、试题

( )

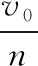
二、试题赏析

(一)以生活情景为载体，考查学生运用创新思维灵活选取物理学原理解决问题的能力

【素材情景】本题属于应用类试题，以红血球受粘滞阻力下落这一实际情境，考查随速度成正比的阻力作用下物体的运动规律。

遇到新情景问题的正确解决方法，一是从必备知识的最根本原理出发，找到最合适的规律、方法解决问题；二是从创新思维出发，找到以前学过的与之条件相似、运动规律相似的物理模型，用相似的规律去解决新问题。

学生无论用哪一种方法解决问题，都是必备知识、关键能力和物理核心素养的良好体现。

此题通过应用性的考查，巧妙的兼顾了基础性、综合性、创新性。

(二)考查力与运动关系的主干必备知识，帮助学生认清错误认识，培养运动与相互作用观的学科素养

题干已知力的特点，选项考查运动关系。教学中可引导学生学会通过审题归纳考点：力与运动的关系。

力与运动的关系是高中物理的主干必备知识，也是新高考评价体系中的物理学科核心素养中最核心的物理观念：运动与相互作用观。那么高中物理的运动与相互作用观又包括哪些呢？此题的研究对象只涉及单个物体，对单个物体的力学三大规律即是：牛顿第二定律、动量定理、动能定理。因为此题合力是变力，又是求位移这种过程量的比例，应该优先选用表达过程的规律，即从动量定理和动能定理中选择。

在选用规律时，此题暴露了学生概念不清的问题。

觉得此题无从下手的同学，就是因为没找到最合适的规律来解决问题。有的同学虽然选出答案C，其实没有真正弄懂，是碰巧出选了正确答案。

因为此题涉及力、位移、始末速度，很多同学按常规思路优先选用动能定理列方程。

然后因为F与v成正比，就说F均匀变化，认为平均作用力为始末力的一半，得表达式

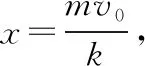
可知x与v0成正比。

选出答案C，恰好是正确选项。这也是此题得分率不算低的一个原因。

但是此题是已知F与v成正比，并不是已知F与x成正比，要先证明F与x成线性关系，才能在求功时认为平均作用力等于始末力的平均。

而且，这些学生认为画出的v-x图应该是弯曲的，斜率是减小的，理由是因为速度变化、阻力变化，所以加速度是变化的。

以上都是因为学生没有把物理量对时间的变化率和对位移的变化率区分清楚，没有分清对时间取平均值和对位移取平均值是两个不同的概念。

混淆这两个概念会出现一些典型错误，比如机车以恒定功率启动的问题中，把加速度减小的加速过程用平均力、平均加速度看成匀变速运动，用牛顿第二定律和运动学公式联立求解，学生发现结果与参考答案不一样，与老师交流才知道，对时间取平均值和对位移取平均值是两个不一样的概念。

只是武汉四月联考第7题的模型恰好是运动的总位移x与初速度v0成正比。

【解题思路】选取一个极短暂的时间Δt，假设红血球的质量为m，在时间Δt之后，红血球的速度变为v，则在该段时间内可将红血球的受力近似认为kv，运用动量定理，有-FΔt=mv-mv0，F=kv，则在红血球达到最大位移时，有kx1=mv0，kx2=mv0/n，可得C项正确。

【答案】C

所以，命题人想考查的必备知识：动量和动量定理。

(三)以关键能力和核心素养的考查促进学生回归课本，有效地培养关键能力和核心素养

【关键能力】本题考查的关键能力主要是理解能力、模型建构能力、分析推理能力。需要考生理解题意，建立正确的物理模型，以微元的思想将变力问题转化成恒力问题。

【学科素养】本题考查的物理核心素养主要是科学思维。主要包括模型建构、科学推理、科学论证、质疑创新等。

【学科思想方法】模型思维、极限思维

1.理解、分析推理等关键能力的考查，利于培养学生科学推理、科学论证的科学思维

能否快速选择合适的规律解决问题是物理关键能力和学科核心素养的表现。

已知力求运动时，力学三大规律选哪个规律最方便？此题是描述一个过程的规律，而速度对时间的累积正是位移！所以，动量定理解决此题最简洁！

命题人的意图是希望考生理解题意，建立正确的物理模型，以微元的思想将变力问题转化成恒力问题。

我认为，微元法会增加学生的心理负担。高考中对关键能力和科学思维的考查其实都是可以在课本找到原型的。

此题回归课本的根本原理和思维方法，是变力的冲量问题。课本有例题“棒球击球的动量定理应用”情景，一段过程中方向不变只有大小变化的变力的冲量可用平均作用力与时间的乘积来表示，而过程中的位移可用平均速度与时间的乘积来表示，两个平均值都是对时间取平均。

2.模型建构等关键能力的考查，有利于促进学生形成归纳总结的习惯，培养模型建构、质疑创新的科学思维

遇到新模型，我们可以引导学生归纳新结论。

质疑创新：难道只有初速度与总位移有正比关系吗？此题答案如此简洁，是否暗含一个更简洁的规律？有没有什么量不变？怎样寻找不变量？

教学中可以引导学生进一步思考：此题的难点在于加速度是变化的，即速度对时间的变化率是变化的，用牛顿运动定律不好判断；但根据以上分析，此题的运动模型似乎有什么特点？如果从运动过程中任意时刻开始计时，以后的运动，是不是都可以同理推出剩下要运动的位移与此刻的速度成正比？那么此题的运动模型有什么特点，能否画出运动过程中的v-t图？

由前文分析可知，运动速度与位移的关系如图。

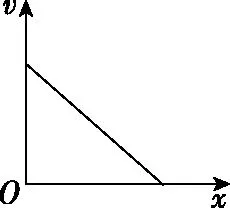
此题结论：若是合外力与速度成正比的减速运动，则运动总位移与初速度成正比。

创新结论1：若是合外力与速度成正比的减速运动，则从任意时刻算起，后面还需要运动的总位移都与该时刻的速度成正比。

创新结论2：若是合外力与速度成正比的减速运动，则运动的速度随位移均匀减少。即整个运动过程都符合规律——单位位移内速度的减少量相同。

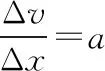
另类加速度概念可回归课本：伽利略对自由落体运动的研究。最开始就猜想速度是否随位移均匀变化？不过最后发现自由落体的速度是随时间均匀变化。所以大家熟知的匀变速运动是合外力不变、速度随时间均匀变化的运动。

但并不表示速度随位移均匀变化的运动不常见。我们稍加引导就会让学生回忆起相关常见模型，比如电磁感应中的水平光滑单杆模型。所以，此题的模型建构有其重要意义。

3.特殊值法、极限法、排除法的运用也可巧妙得出答案，体现了题目的开放性，利于培养学生的创新能力

有的同学用特殊值代入的排除法也选出了正确答案。排除法也是创新能力的体现，此题的题型是选择题，学生对题目情境蕴含的本质规律还不是很清楚时，应鼓励学生运用特殊值、极限法、排除法等巧解妙解。

创新思维的一个重要功能是化繁为简，有很多单选题可以运用创新思维化复杂模型为简单模型，单位是否符合？用极限法变为理想模型时表达式是否符合？取特殊值变为对称模型时表达式是否符合？极限外推理模型、特殊值法、对称模型等是解决选择题中复杂问题的常用创造性思维。

三、对课堂教学的指导意义：以创新思维能力的培养带动必备知识的巩固、关键能力的强化、核心素养的培养，有事半功倍的效果

笔者认为，此题最大的亮点就是考查了类比思维这种重要的创新思维能力，此题能让学生更深刻地认识类比思维的妙用。单纯从理论上指导如何选择规律，显得比较枯燥，学生不容易在短时间找到突破难题的方法。教学中可以用以前熟悉的模型类比，让学生亲身感受到化陌生为熟悉，变未知为已知的神奇，让他们自己得出解题方法，让他们感知物理的智慧，这种兴奋的刺激会让他们记忆深刻。这样学生既有成功的快乐感，又觉得顺其自然的理解没有难度，而且还容易形成从特殊到一般、普遍联系的哲学思想，养成归纳总结的好习惯，对培养学生的科学素养有好处。

类比思维能力是高考常考的创新思维能力，是解决新问题常用的思维方式。我猜想出题人可能就是受某常规题的启发，创造性地变式出的这个原创题。

笔者是按这样的程序讲解这道题：

先要同学们说出此题中红细胞的受力特点，学生说出力与速度成正比。

笔者再要学生们回忆以前学的哪些力与此相似。

学生很快答出洛伦兹力、机车启动的牵引力、空气阻力等；因为有空气阻力的抛体和机车启动模型比较复杂，受牵引力还受阻力、受空气阻力还受重力，还有什么模型与这个更接近？马上就有学生说：“电磁感应中的安培力！”

笔者画出光滑水平面上只有初速度的单棒模型，提问：我们当时是用什么规律列方程分析的？

学生很快答出动量定理。

笔者问如果还是用电磁感应的情景出题，你们是不是会做？

学生们回答会做！因为已经多次讲过这种动量定理在电磁感应中综合应用的模型。

笔者又问你们是只满足于做对这一个题目，还是总结了一类问题的解决方法呢？有没有总结这种受力条件与运动性质的对应关系呢？

此题是合外力与速度成正比的减速运动，运动特点应该是速度与位移是线性关系。

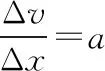
虽然这不是课本上专门讲过的一种运动，却也是一种很简洁很有特点的运动。而且是电磁感应中的一类常见运动，研究并记住它很有必要。

如果熟练总结了各类运动特点对应的受力条件(必备知识)，我们就可以用类比的科学思维(核心素养、关键能力)来应对新情景问题，轻松找到解决新问题的思路方法。这就是高考专家出题要考查创新思维的出发点。也是高考出创新题的常见方式！

四、对原创或改编习题的启示

利用新情景考查科学思维和主干知识的根本原因是新高考考题的重要特点，我们在习题教学中也要让学生适应。模型建构、类比、等效、比较、极限等都是高考常考的创新思维，是科学研究中对发明发现有关键作用的能力，所以几乎每一次高考都会考查。命题人希望学生能学以致用、举一反三，我们也希望我们的课堂教学“有事半功倍”的效果。