“三步”求解天体运动中的比值问题
2021-07-14四川
四川
(作者单位:四川省渠县中学)
对于天体运动问题,很多同学得分较低,原因包括以下三个方面:一是未建立起“中心天体圆周运动轨道模型”;二是“圆周运动、万有引力、卫星”的关系让学生混乱不清;三是涉及综合知识的关系式和物理量众多,遇到求解比值问题,学生更是毫无头绪,要么感觉计算繁琐,直接放弃,要么化简时出现颠倒错误。天体运动这一章,归根到底,考查核心是万有引力提供向心力,需要解决中心天体的质量和密度的问题,用到的方法有“表面物体法”和“引入卫星法”。笔者通过归纳总结多届学生的错因,提炼出求解天体运动涉及比值问题的“三步法”。该方法能够简化书写过程,让比值的形式简单,节约时间,降低出错率,甚至可以迁移至任意求解比值问题,从而提高学生学习物理的积极性。接下来通过例题分析说明“三步法”求比值的便利和特点:
第一步:找准原理式
第二步:求解未知量
第三步:化简比例式
一、天体运动中求比值
【典例1】(2021·河北卷·4)“祝融号”火星车登陆火星之前,“天问一号”探测器沿椭圆形的停泊轨道绕火星飞行,其周期为2个火星日。假设某飞船沿圆轨道绕火星飞行,其周期也为2个火星日。已知一个火星日的时长约为一个地球日,火星质量约为地球质量的0.1倍,则该飞船的轨道半径与地球同步卫星的轨道半径的比值约为
( )
【分析】常规方法求解:
根据“引入卫星法”及万有引力提供向心力可知:
则有:

(在化简求比值时,由于涉及物理量较多,计算时极易出错,并且书写用时较长)
“三步法”求解:
第一步,找原理式,根据卫星围绕中心天体做匀速圆周运动及题目已知,有:

第二步,求未知量,表示出正比例关系,故:

第三步,求解比值:

【答案】D
【典例2】据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的24倍。不考虑自转效应,该行星表面的重力加速度是地球表面重力加速度的6倍,由此可推知,该行星的半径与地球半径的比值约为
( )
A.0.5 B.2 C.3.2 D.4
【分析】常规法求解:
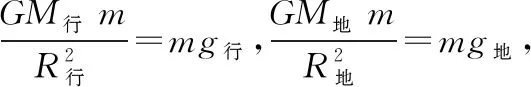
“三步法”求解:
第一步,找原理式:
第二步,求未知量:
第三步,求解比值:
【答案】B
【步骤说明】
1.处理第一步时,即使是多个对象,也只需写出原理式一次即可,这样就可以少书写公式,在天体运动部分物理量众多的情况下,更能节约时间;
2.在第二步求未知量时,使用“∝”,巧妙地将两个对象具有相同的物理量以及常数部分约去(因为求比值时,相同物理量和常数将会比值为1),简化了比值决定式的形式;
3.第三步求解比值,成正比时,角标正对应,成反比时,角标反对应,巧妙避免处理多个分数的麻烦,有效降低出错率。
【总结】很多同学看到此类试题就不愿意分析,“排斥心理”的逐渐堆积致使求比值成为得分难题。分析原因:一是学生对天体部分模型建立不熟悉,感觉很茫然,不知从何分析;二是即使会分析和列式子,但涉及到演算,因繁琐复杂,易算错,一旦演算不顺利,学生就会立即放弃。久而久之,很多同学不再愿意做此类题型,产生排斥心理。
【典例3】甲、乙两星球的平均密度相等,半径之比是R甲∶R乙=4∶1,则这两个星球表面的重力加速度之比是
( )
A.1∶1 B.1∶4 C.1∶16 D.4∶1
【分析】“三步法”求解:

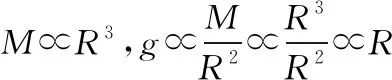
【答案】D
【典例4】两个行星A和B各有一颗卫星a和b。卫星的圆形轨道接近各自行星的表面。如果两行星质量之比MA∶MB=p,两行星半径之比RA∶RB=q,则两卫星周期之比Ta∶Tb为
( )

【分析】“三步法”求解:
第一步,找原理式,根据“引入卫星法”,故原理式为:

【答案】A
二、迁移——求任何比值问题
【典例5】如图1所示,在坡度一定的斜面顶点以大小相同的初速v同时水平向左与水平向右抛出两个小球A和B,两侧斜坡的倾角分别为37°和53°,小球均落在坡面上,若不计空气阻力,则A和B两小球的运动时间之比为
( )

图1
A.3∶4 B.4∶3 C.9∶16 D.16∶9
【答案】C
【分析】“三步法”求解:
第一步,找原理式,两球做平抛运动,涉及竖直方向的自由落体运动和水平方向的匀速直线运动,其原理式为:
第二步,求未知量,因两球的初速度大小相等,故:
第三步,求解比值:
【答案】C
【典例6】两个电荷量分别为q和-q的带电粒子a和b分别以速度va和vb射入匀强磁场,两粒子的入射方向与磁场边界的夹角分别为30°和60°,磁场宽度为d,两粒子同时由A点出发,同时到达B点,已知A、B连线与磁场边界垂直,如图2所示,则
( )

图2
B.两粒子的质量之比ma∶mb=1∶2
C.a粒子带正电,b粒子带负电
D.两粒子的速度之比va∶vb=1∶2
【分析】“三步法”求解:
作出其中一个粒子的运动轨迹图(如图3),由选项可知,需求解R、m、v0三个物理量之比。

图3
第一步,找原理式,根据粒子在磁场中做匀速圆周运动的规律以及几何知识,故需要的原理式有:
第二步,求未知量,直接求解正比例关系即可,电荷量相等、运动时间相等、相同磁感应强度和磁场宽度,故:
第三步,求解比值:
【答案】B
总结:此题涉及物理量较多,应用三步法,使学生思路清晰、目标明确,利用正比关系,将相同物理量提前约去,让最终比例式简洁明了,降低出错率。
【典例7】如图4所示,a、b两个闭合正方形线圈用同样的导线制成,匝数均为10匝,边长la=3lb,图示区域内有垂直纸面向里的均强磁场,且磁感应强度随时间均匀增大,不考虑线圈之间的相互影响,则a、b线圈中电功率之比为
( )
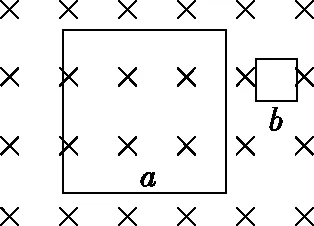
图4
A.1∶1 B.3∶1 C.9∶1 D.27∶1
【分析】“三步法”求解:
第一步,找原理式,涉及法拉第电磁感应定律、电阻定律和电功率,故需要的原理式有:
第二步,求未知量,因材质相同,磁感应强度的变化率相等,故:
【答案】D
【典例8】如图5所示,从离子源产生的甲、乙两种离子,由静止经加速电压U加速后在纸面内水平向右运动,自M点垂直于磁场边界射入匀强磁场,磁场方向垂直于纸面向里,磁场左边界竖直。已知甲离子射入磁场的速度大小为v1,并在磁场边界的N点射出;乙离子在MN的中点射出;MN长为l,不计重力影响和离子间的相互作用。求:

图5
(1)磁场的磁感应强度大小;
(2)甲、乙两种离子的比荷之比。
【分析】第(2)小问求比荷之比,利用“三步法”求解:
第一步,找原理式,涉及离子在静电场中加速运动(动能定理)和在磁场中做匀速圆周运动(洛伦兹力提供向心力),故需要的原理式有:
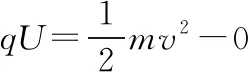
第二步,求未知量,联立两式消去速度v(将②式中的v解出代入①式),并且两离子经过相同电场加速和相同磁场偏转,故有:

