从不同角度证明一道粒子运动题
2021-07-14安徽
安徽
(作者单位:安徽省太和县宫集镇中心学校安徽省阜阳市教育科学研究所)
本文采用三种不同方法对2020年全国高考物理卷Ⅰ中的一道选择题目的推理依据进行逻辑论证;将解决问题的方法推广到一般情形,给出这道选择题目的多个变式并进行求解。
一、原题呈现
( )
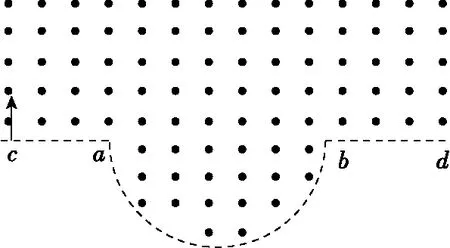
图1
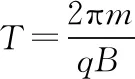
即,该题目的正确选项是C。

图2
由于这道题目是选择题,作答时无需写出推理过程,所以,从应试的角度考虑,根据作图的“直观”感受进行选项的判断无疑是最省时同时又最“省劲”的方法。那么其正确性如何进行证明呢(很多学生是凭作图结果进行选择的,因为他们没有找到证明的方法,这不能不说是一种侥幸)?
二、C选项正确性的证明
1.运用求导方法进行证明

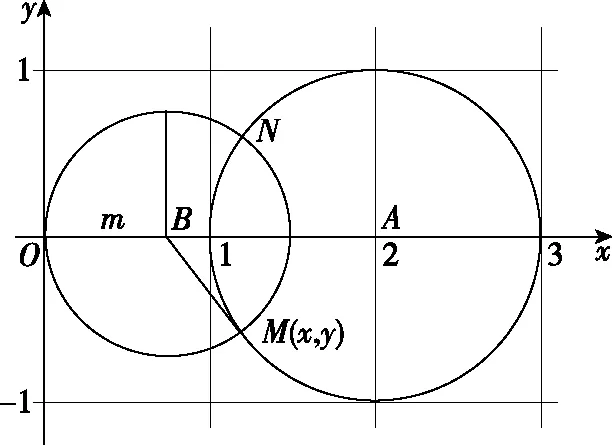
图3
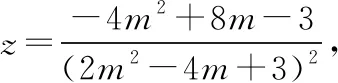
∵2m2-4m+3>0

2.运用余弦定理进行证明
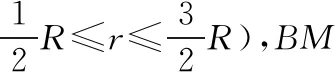
易知,当r=R时,cosθ最小,此时θ最大(证毕)
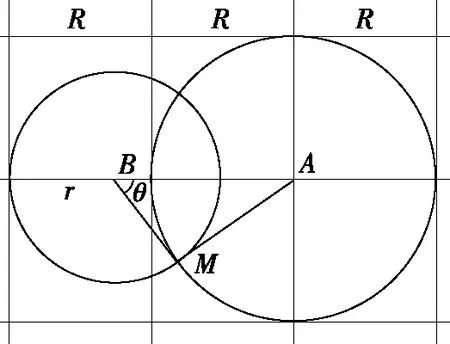
图4
3.运用直线与图形的位置关系进行证明
如图5所示,⊙A下方的半圆是磁场的边界,由P点按题目要求射出的很多速率不同的粒子在磁场中沿圆弧轨迹运行之后与圆形磁场边界的交点分别是B、C、D…,设某粒子的轨迹和磁场边界的交点与P点的连线与PA的夹角为α,轨迹圆弧所对的圆心角为θ,易知θ=180°+2α,显然,当α最大时θ最大,由图5可知,在P与⊙A上各点的连线中,其中过P点的切线与PA的夹角最大,而PA的长度是⊙A半径的2倍,所以轨迹圆的半径与磁场边界圆的半径相等时,P与两圆交点的连线刚好是轨迹圆的切线,此时轨迹圆弧所对的圆心角最大,粒子在磁场中运动的时间最长。
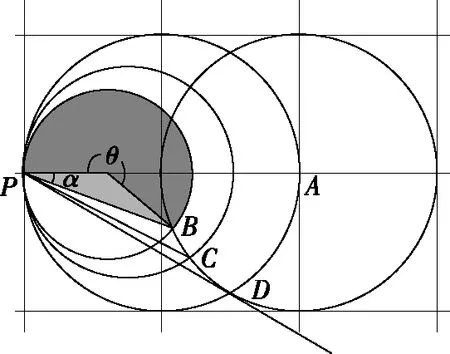
图5
三种证明方法相比,显然方法3是最简便易懂的方法。
应该说,采用方法三,很容易从众多大小不等的圆形轨迹中,确定在磁场中按题目所给条件进行运动的带电粒子运行时间最长的轨迹。实际上,方法三不仅限于解决这一个问题,而是可以解决跟例题1类似的同一类型的不同问题。我们不妨看下该方法在解决类似问题中的应用。
三、该高考题目的多个变式及解析
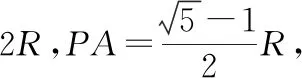
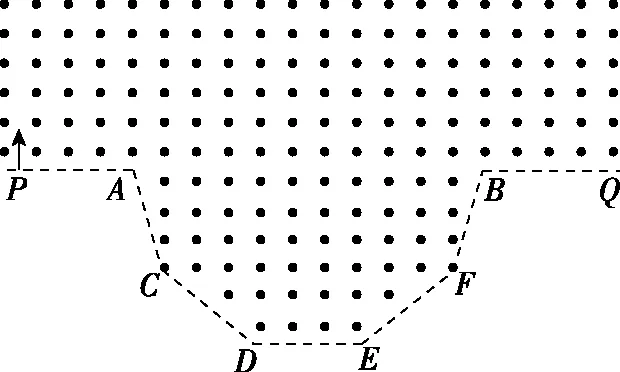
图6
【解析】如图7所示,设正十边形的中心为O点,边DC的延长线交直线AB与M,我们先判断粒子的射入点P相对M的位置。
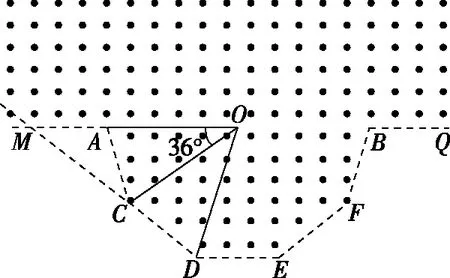
图7
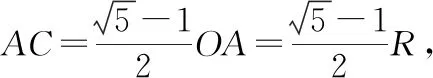
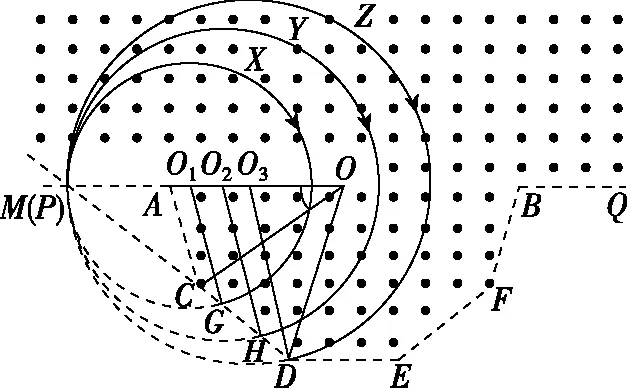
图8
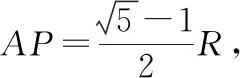
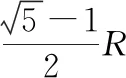
【变式2】一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图9中虚线N-A-C-M所示,其中曲线AC段为抛物线的一部分,C为抛物线的顶点,磁场边界的其余部分为直线。一束质量为m、电荷量为q(q>0)的粒子,在纸面内从P点垂直于PA射入磁场,这些粒子具有各种速率。已知抛物线的水平弦长AB=8,抛物线顶点C到AB的距离也为8,PA=1,不计粒子之间的相互作用,求粒子在磁场中运动的最长时间(结果可保留反三角函数)。
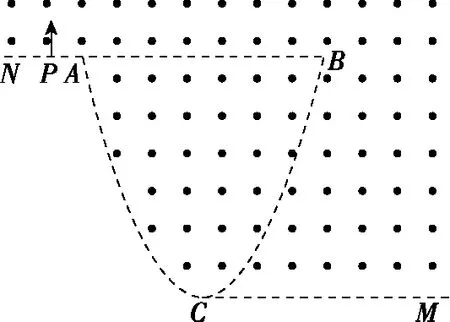
图9
【解析】如图10所示,从粒子的发射点P作抛物线的切线,设切点为E,以E为顶点作∠PEF=∠EPB,角的另一边交AB与F,由以上分析可知,PE与PB的夹角∠EPB是P点与抛物线上各点连线中与PB夹角最大的角,所以,从E点射出的粒子在磁场中运行的时间最长,这时点F为运行时间最长的轨迹圆的圆心。
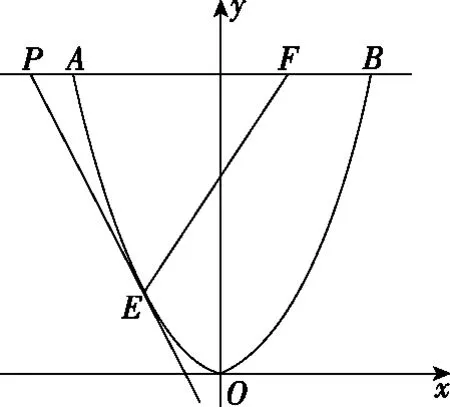
图10
四、结语

