牵连体加速度问题解析

湖北

(作者单位：武汉华中科技大学附属中学)

加速度是联系运动学与力学的桥梁。求加速度一般有两种思路：其一是根据物体的运动情况由运动学规律求加速度；其二是根据物体的受力情况由牛顿第二定律求加速度。对于牵连体的加速度问题，若牵连体内物体的加速度不同，它们的加速度往往存在某种关联，而这种关联又受具体的物理情景所制约。寻找牵连体内物体加速度之间的隐含制约关系，是此类问题分析求解的一个难点。本文通过实例分析，分类总结求解牵连体加速度问题的思维方法。

一、直连体

相互接触的两物体，若两物体在相对运动过程中始终不脱离接触，则在运动的任意时刻，两物体在垂直于接触面方向上(或法向上)有相同的分加速度。

1.加速度恒定

求解各自加速度恒定牵连体的加速度，可根据物体的受力情况由牛顿第二定律列式求解，但要找出牵连体中物体加速度间的隐含关系；也可以假设经过一段运动过程，由能量、动量等相关规律得出此过程中物体获得的速度，再由运动学规律求物体的加速度。

【例1】如图1，质量为M、倾角为θ的三角形物块A置于光滑水平面上，三角形物块A的斜面光滑。将质量为m的小滑块B轻放在A的斜面上。已知重力加速度为g，滑块B在物块A的斜面上滑动过程中，求滑块B的加速度a的大小。

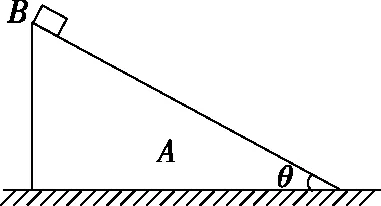
图1

【分析】由于水平面光滑，当滑块B沿斜面下滑过程中，物块A沿水平面向左做直线运动。如图2所示，以地面为参照物，某时刻设滑块B的加速度a方向与竖直方向成角α；其水平向右的分量为ax，竖直向下的分量为ay，物块A方向水平向左的加速度为a2。滑块B受重力mg与A对B的弹力FN的作用，其合力为ma；物块A受重力Mg、B对A的弹力FN(为简化符号运算，这里将A对B的弹力大小与B对A的弹力大小均记为FN)，B在A的斜面上滑动的过程中，两物体间的相互作用力FN的大小与B在A上位置无关，为一恒定值，可知A、B两物体均做匀变速直线运动，两物体各自的加速度恒定。

【解法1】如图2，对A、B两物体分别由牛顿第二定律有：

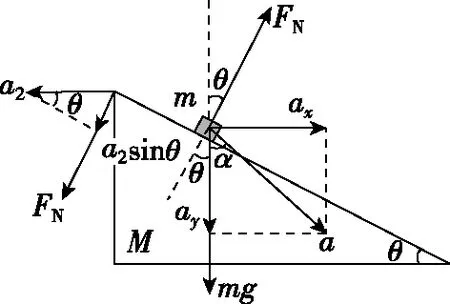
图2

FNsinθ=Ma2

FNsinθ=masinα

mg-FNcosθ=macosα

两物体在垂直斜面方向上的分加速度相等，即

a2sinθ=acos(α+θ)

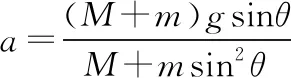
【解法2】设水平面对A竖直向上的支持力为F0，A的合力为Ma2。两物体受力与合力的矢量图如图3所示。由矢量间的几何关系有：

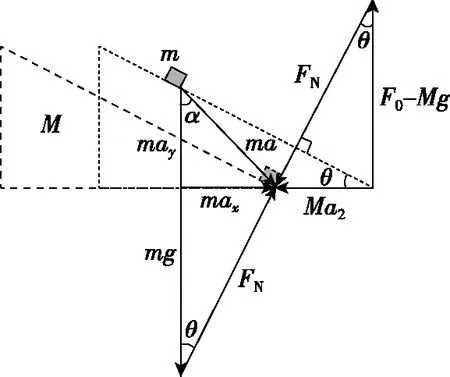
图3

FNsinθ=Ma2=max

mgcosθ=FN+Ma2sinθ

may=(Ma2+max)tanθ

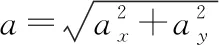
由以上几式可得a的值(同上)。

【解法3】以斜面体A为参考系，滑块B受到一个水平向右的惯性力ma2，如图4所示。有：

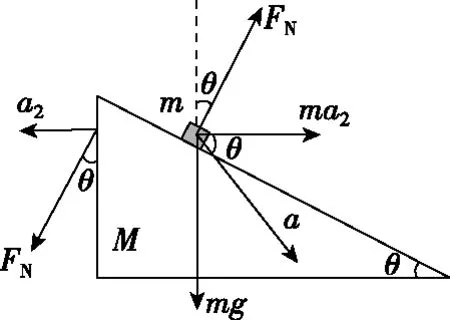
图4

FNsinθ=Ma2

FNsinθ+ma2=max

mg-FNcosθ=may

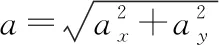
由以上几式可得a的值(同上)。

【解法4】设斜面体A的斜面高为h，底边长为L，滑块B从斜面顶端下滑至底端时的水平、竖直分速分别为vx、vy，斜面体A的速度为v2(如图5所示)。B在A上下滑过程中，系统水平方向动量守恒，有：mvx=Mv2，可得：m(L-x)=Mx；

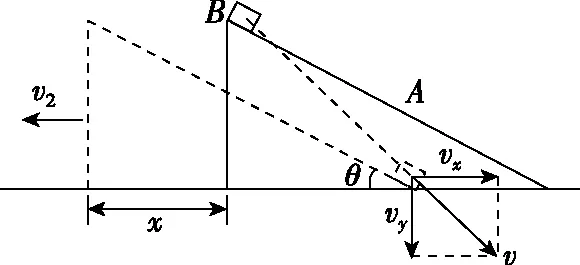
图5

由机械能守恒定律有：

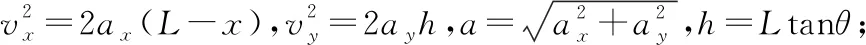
由以上几式可得a的值(同上)。

【点评】解法1在正确分析物体受力的基础上，分别在水平方向与竖直方向利用牛顿第二定律列出动力学方程，再找出两物体加速度的隐含关系，即在运动过程中两物体不脱离接触，两物体在垂直于接触面方向上(即垂直斜面方向)有相同的分加速度；这是一种基本解法，求解关键要注意牛顿第二定律的矢量性。解法2基于物体受力与合力(ma)的矢量图形，利用矢量间的几何关系求解；此法求解关键是正确画出物体受力与合力间的矢量图形，利用几何图形找出隐含的几何关系，这是一种实用的解法。解法3选取斜面体A为参照系，这是一个非惯性系，为在非惯性系应用牛顿第二定律，在对滑块B的受力分析中引入了一个惯性力，虽然超出目前中学物理知识范围，但此法是值得掌握的一种简洁方法；以上三种解法均是基于力与运动的观点，利用牛顿运动定律结合直连体间加速度的隐含关系进行求解；解法4则是从运动学的观点求加速度，假设物体运动一段过程，利用动量守恒定律与机械能守恒定律求出此过程中物体的末速度，再根据运动学公式求解，求解时要注意物体速度、加速度的分解与合成，在矢量运算下求解，这是一种巧妙的解法。

2.加速度变化

求解牵连体的变化的加速度，一般是求解某一具体位置(或时刻)的加速度。可根据物体在此位置的受力情况由牛顿第二定律列式求解，但要找出牵连体中物体加速度间的隐含关系。也可以假设经过一段很小的运动过程，由能量、动量等相关规律求出此小段过程中物体获得的速度，再由运动学规律与极根分析，求出物体在某位置(或时刻)的加速度。

【例2】质量均为M、圆心分别为O1、O2的两相同大环重叠竖直放在光滑水平面上，一质量为m的小环C套接在两大环的最高点。受一微小扰动，两大环由静止开始分别沿水平面向左、右运动，小环C则从静止开始竖直向下运动(如图6所示)。当∠CO1O2=θ时，求小环加速度a的大小。

【分析】根据对称性，同一时刻或同一位置，两大环对小环的弹力FN大小相等，方向与竖直方向夹角相同；但在小环运动到不同位置处，FN方向不同，即FN与位置有关，可知两大环与小环均做变加速直线运动。当位置一定时，大环与小环的加速度大小一定。求某一确定位置(∠CO1O2=θ)时小环加速度a的大小，可根据此位置小环受力情况由牛顿第二定律求出，也可以根据运动学规律通过极限分析求出。

【解法1】如图7，设此时大环O2的加速度大小为a2，方向水平向右。对小环与大环分别由牛顿第二定律有：

mg-2FNsinθ=ma

FNcosθ=Ma2

小环与大环不脱离接触，在运动的任意时刻，小环与大环沿连心线方向的分加速度大小相等，即：asinθ=a2cosθ

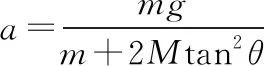
【解法2】建立如图8所示坐标系，设大环的半径为R，此时小环C的竖直位置坐标为yC=Rsinθ，大环O2的横坐标位置为x2=Rcosθ。

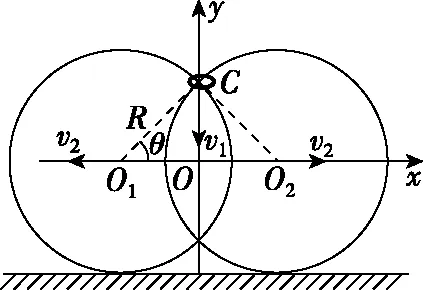
图8

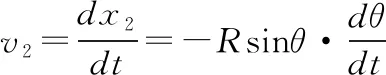
可得此时小环与两大环速度的大小关系为：v2=v1tanθ

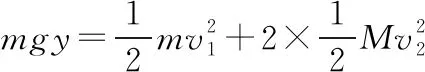
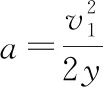
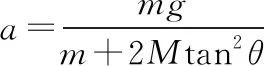
【点评】解法1是一种动力学解法，在正确分析此位置小环与大环受力的基础上，根据牛顿第二定律列出动力学方程，求解中要根据直连体的特点找出牵连体内物体间加速度的隐含关系；解法2是一种运动学解法，假设此位置后经过一小段运动过程，根据小环与两大环运动特点与对称性，找出小环与大环隐含的速度大小关系，利用机械能守恒定律求小环获得的速度，再根据运动学规律通过极限分析得出此时小环的加速度大小。

二、绳连体

用拉紧的细绳连接两物体，同一时刻两物体的运动方向不一定都沿细绳方向，在同一时刻两物体沿细绳方向的加速度不一定相等。在绳上张力大小未知的情况下，我们可以运用假设法找出绳连体物体间加速度的制约关系；或根据具体问题条件，结合物体的运动情况与特点，运用微元法、几何法找出绳连体物体间的速度、位移等关系式，再运用数学方法求导得出绳连体物体间加速度的制约关系。

【例3】如图9所示，光滑直杆与水平方向成θ角固定，杆上套一质量为mA的小环A，环下用一轻绳连一质量为mB的小球B，开始时用手持住环使A、B处于静止状态，且轻绳保持竖直，已知重力加速度为g，则在释放环A的瞬间，小球B的加速度大小为多少？

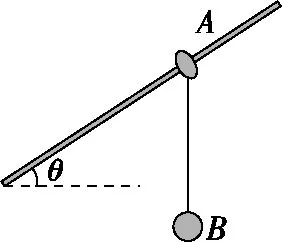
图9

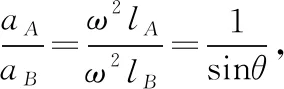
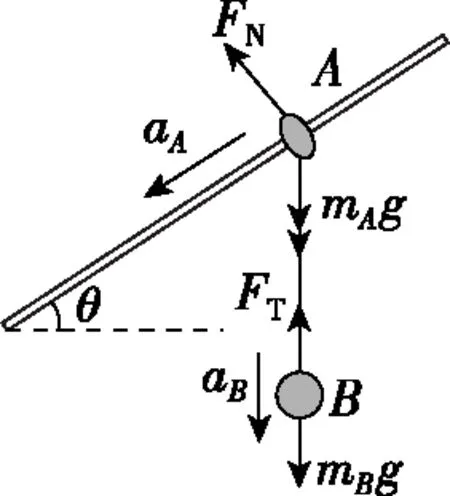
图10

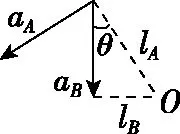
(a)

【解析】释放环A的瞬间，对A、B两物体由牛顿第二定律分别有：

(mAg+FT)sinθ=mAaA

mBg-FT=mBaB

又aB=aAsinθ

【点评】物体的速度为零时加速度不一定为零。本题中小环A受杆的制约，只能沿杆运动，其加速度方向沿杆向下，沿绳方向存在分加速度；释放小环A的瞬间，连接A、B间的细绳呈竖直状态，小球B受到的重力与细绳的拉力均沿竖直方向，此时小球B的加速度沿竖直方向(即沿此时的细绳方向)。以上分析中运用假设法、微元法找出A、B两物体加速度的关联。用拉紧的细绳连接的两物体，当两物体的速度为零或均沿绳方向运动时，由于细绳不可伸长，则同一时刻两物体沿细绳方向有相同的加速度。

【例4】如图12所示。一轻绳绕过光滑的小定滑轮，其两端分别连接两小物体A、B，其中物体B套在固定光滑竖直杆上，杆与小定滑轮相距l。已知物体A竖直向下运动，物体B沿杆向上运动，当轻绳与竖直杆夹角为θ时物体B的速度大小为v，加速度大小为a，求此时物体A的加速度大小aA。

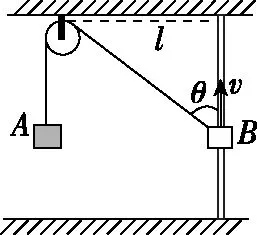
图12

【分析】设此时物体A的速度为v1，方向向下；物体B的速度v沿杆向上，不沿绳方向，物体B相对小定滑轮既做平动又做转动。如图13所示，将物体B的速度与加速度分别向沿绳方向与垂直绳方向分解，沿绳方向的分速度v1与物体A的速度大小相等；其中分量a1改变v1的大小，分量a2改变v2的方向。

【解法1】如图13，v1=vcosθ，v2=vsinθ。由于v1与θ均随时间t发生变化，则有：

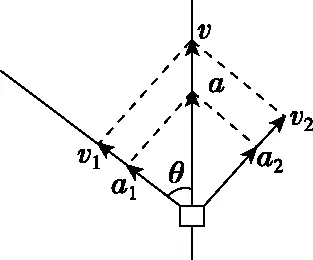
图13

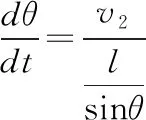
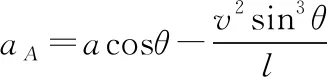
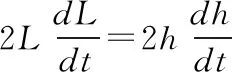
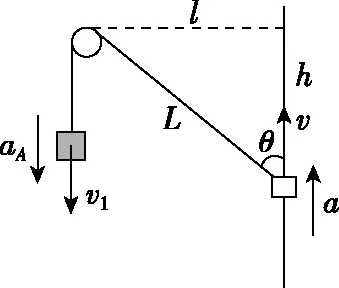
图14

即：Lv1=hv

对等式Lv1=hv两边求导有：

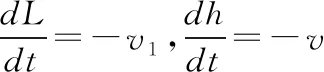
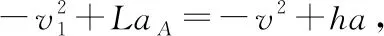
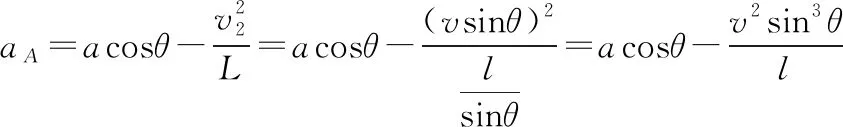
【点评】物体的加速度由物体受到的力与质量决定，与速度无直接关系。绳连体中当物体的速度不沿绳方向时，则相对某一定点，物体可能既有平动又有转动。当绳上的拉力参与提供转动的向心力时，绳上的拉力大小与物体运动速度有关，这时物体的加速度大小在表象上与物体运动的速度有关。这种情况下绳连体间的加速度关系较为复杂，但在运动过程中两物体的位移、速度存在一定的关联。解法1根据两物体运动过程中的速度关联(即物体B沿绳方向的分速度v1等于物体A的速度大小)，通过对速度关系式求导得出两物体加速度大小的关系；解法2根据两物体位移的关联，通过对位置关系式的两次求导得出两物体加速度大小的关系。在求导过程中，要注意分析相关物理量大小的增减及物理意义。